北师大版 数学八年级上册6.3 从统计图分析数据的集中趋势课件(共24张)
文档属性
| 名称 | 北师大版 数学八年级上册6.3 从统计图分析数据的集中趋势课件(共24张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 21:33:22 | ||
图片预览




文档简介
(共24张PPT)
北师大版数学八年级上册
第6章
数据的分析
6.3 从统计图分析数据的集中趋势
1.进一步认识平均数、众数、中位数都是数据的代表,了解它们在描述数据时的差异.
2.会从扇形、折线和条形等统计图中获取信息.
学习目标
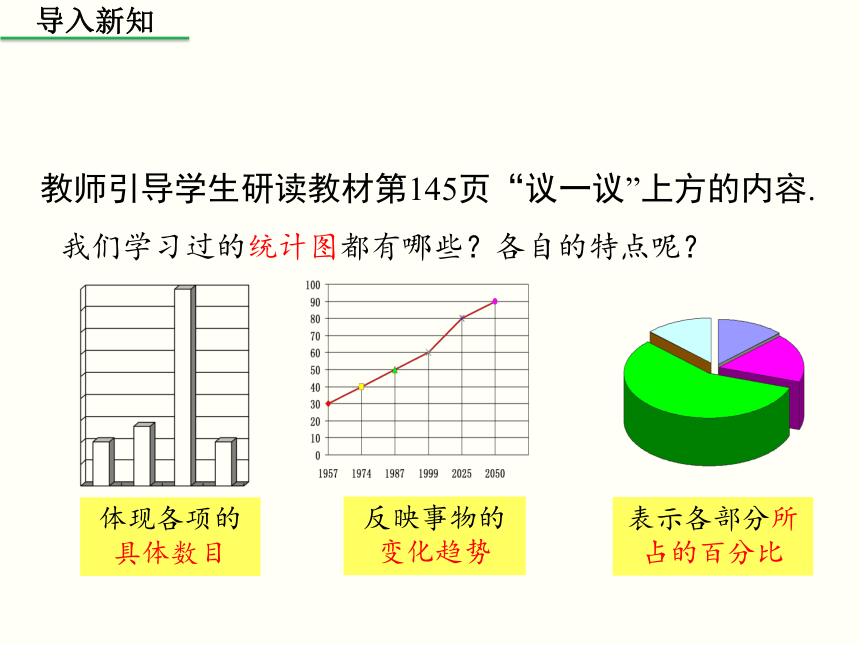
教师引导学生研读教材第145页“议一议”上方的内容.
体现各项的具体数目
反映事物的变化趋势
表示各部分所占的百分比
我们学习过的统计图都有哪些?各自的特点呢?
导入新知
知识模块一 从条形统计图分析数据的集中趋势
自主探究:
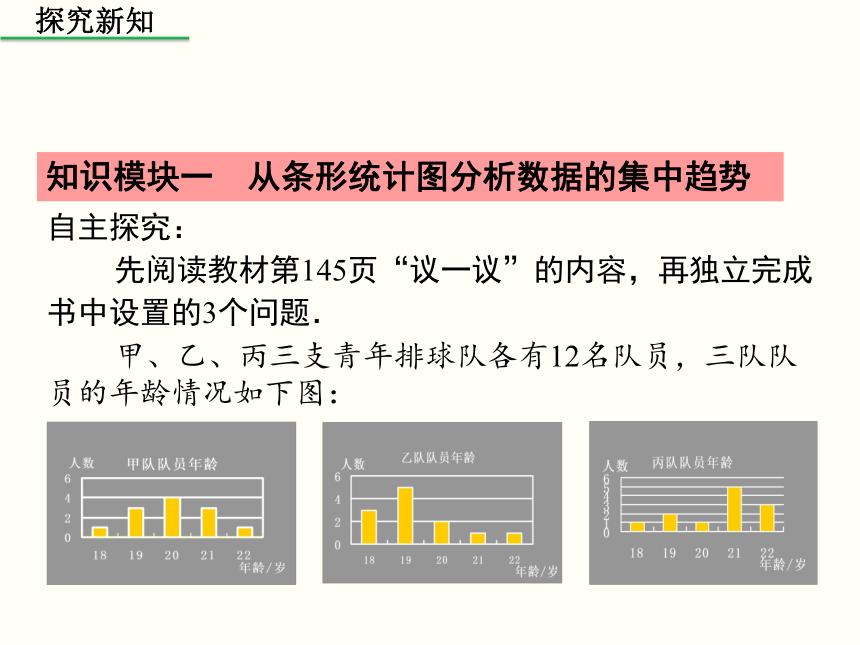
先阅读教材第145页“议一议”的内容,再独立完成书中设置的3个问题.
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
探究新知
(1)
从图中可以看出:
甲队队员年龄的众数是
,中位数是
;
乙队队员年龄的众数是
,中位数是
;
丙队队员年龄的众数是
,中位数是
.
20岁
20岁
19岁
19岁
21岁
21岁
(2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?与同伴交流.
答:丙队队员平均年龄最大,甲次之,乙最小.
(3)计算出三支球队队员的平均年龄,看看你上面的估计是否准确?(分组进行计算)
答:甲、乙、丙三队队员的平均年龄依次是:20岁、19.3岁、20.6岁.
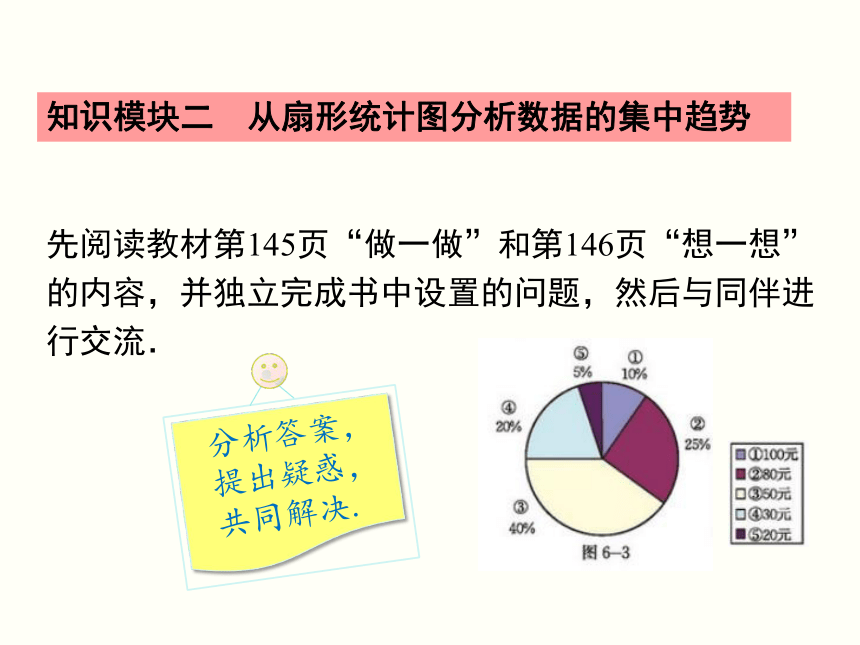
知识模块二 从扇形统计图分析数据的集中趋势
先阅读教材第145页“做一做”和第146页“想一想”的内容,并独立完成书中设置的问题,然后与同伴进行交流.
分析答案,提出疑惑,共同解决.
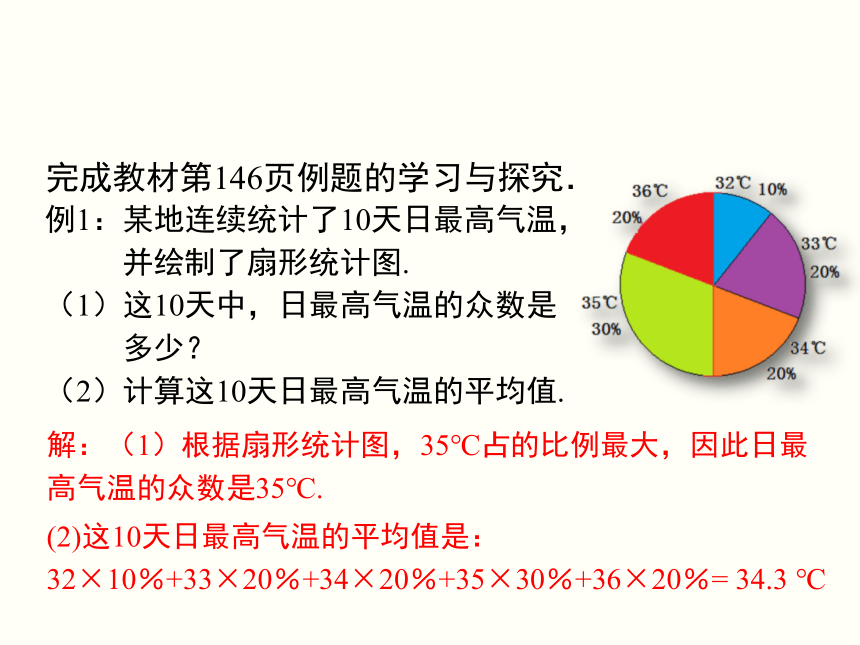
完成教材第146页例题的学习与探究.
例1:某地连续统计了10天日最高气温,
并绘制了扇形统计图.
(1)这10天中,日最高气温的众数是
多少?
(2)计算这10天日最高气温的平均值.
解:(1)根据扇形统计图,35℃占的比例最大,因此日最高气温的众数是35℃.
(2)这10天日最高气温的平均值是:
32×10%+33×20%+34×20%+35×30%+36×20%=
34.3
℃
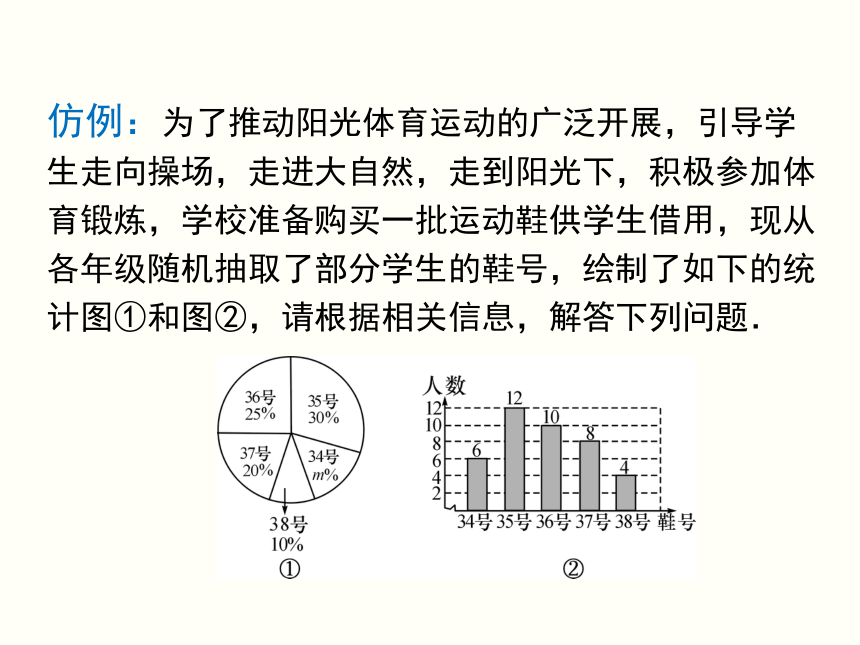
仿例:为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题.
(1)本次接受随机抽样调查的学生人数为
,
图①中m的值为
;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,
建议购买35号运动鞋多少双?
40
15
(2)∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本的众数为35;
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都为36,
∴中位数为
=36;
(3)∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋,有200×30%=60双为35号.
1.数据2、7、3、7、5、3、7的众数是(
)
A.2
B.3
C.5
D.7
D
课堂练习
2.一位经销商计划进一批运动鞋,他到某地的一所学校里对八年级的100名男生的鞋号进行了调查,经销商最感兴趣的是这组鞋号的(
)
A.中位数
B.平均数
C.方差
D.众数
D
3.某班第一小组7名同学的毕业升学体育测试成
绩(满分30分)依次为:25,
23,25,23,27,30,
25,那么这组数据的中位数和众数分别是(
)
A.
23,25
B.
23,23
C.
25,23
D.
25,25
D
5.某次射击训练中,一小组的成绩如下表所示:
解:有4人的成绩为8环
若该小组的平均成绩为7.7环,则成绩为8环的有多少人?
4.一组数据3,4,9,x,它的平均数比它唯一的众数大1,则x=
.
4
6.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分共4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是
.
成绩频数条形统计图
成绩频数扇形统计图
2.95
7.某校八年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,这组数据的中位数是______.
一班学生1~8月课外阅读数量折线统计图
58
8.某商店有200
L,215
L,185
L,180
L四种型号的冰箱,一段时间内共销售58台,其中四个型号分别售6台,30台,14台,8台,在研究电冰箱出售情况时,商店经理关心这组数据的平均数吗?他关心的是什么?
解:商店经理不关心这组数据的平均数,他关心的是众数,也就是哪种型号的电冰箱销量最好.
9.某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工件数
540
450
300
240
210
120
人数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假如生产部负责人把每位工人的月加工零件数定为260件,你认为这个定额是否合理,为什么?
解:(1)平均数:260(件),中位数:240(件),众数:240(件).
(2)不合理.因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260是平均数,但不利于调动多数员工的积极性.因为240既是中位数,又是众数,是大多数人能达到的定额,故定额为240较为合理.
10.三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各抽取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:
甲厂
7
8
9
9
9
11
13
14
16
17
19
乙厂
7
7
9
9
10
10
12
12
12
13
14
丙厂
7
7
8
8
8
12
13
14
15
16
17
试问:(1)这三个厂家的广告分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传?
(2)如果三种产品的售价一样,作为顾客的你会选购哪个厂家的产品?请说明理由.
解:(1)甲厂的广告利用了统计中的平均数.
乙厂的广告利用了统计中的众数.
丙厂的广告利用了统计中的中位数.
(2)选购甲厂的产品.理由是甲厂生产的灯管的使用寿命的平均数能较真实地反映灯管的使用寿命.或选用丙厂的产品.理由是丙厂生产的灯管的使用寿命有一半以上超过12个月.
从统计图分析数据的集中趋势
折线统计图
条形统计图
扇形统计图
总结新知
再
见
北师大版数学八年级上册
第6章
数据的分析
6.3 从统计图分析数据的集中趋势
1.进一步认识平均数、众数、中位数都是数据的代表,了解它们在描述数据时的差异.
2.会从扇形、折线和条形等统计图中获取信息.
学习目标
教师引导学生研读教材第145页“议一议”上方的内容.
体现各项的具体数目
反映事物的变化趋势
表示各部分所占的百分比
我们学习过的统计图都有哪些?各自的特点呢?
导入新知
知识模块一 从条形统计图分析数据的集中趋势
自主探究:
先阅读教材第145页“议一议”的内容,再独立完成书中设置的3个问题.
甲、乙、丙三支青年排球队各有12名队员,三队队员的年龄情况如下图:
探究新知
(1)
从图中可以看出:
甲队队员年龄的众数是
,中位数是
;
乙队队员年龄的众数是
,中位数是
;
丙队队员年龄的众数是
,中位数是
.
20岁
20岁
19岁
19岁
21岁
21岁
(2)根据图表,你能大致估计出三支球队队员的平均年龄哪个大、哪个小吗?你是怎么估计的?与同伴交流.
答:丙队队员平均年龄最大,甲次之,乙最小.
(3)计算出三支球队队员的平均年龄,看看你上面的估计是否准确?(分组进行计算)
答:甲、乙、丙三队队员的平均年龄依次是:20岁、19.3岁、20.6岁.
知识模块二 从扇形统计图分析数据的集中趋势
先阅读教材第145页“做一做”和第146页“想一想”的内容,并独立完成书中设置的问题,然后与同伴进行交流.
分析答案,提出疑惑,共同解决.
完成教材第146页例题的学习与探究.
例1:某地连续统计了10天日最高气温,
并绘制了扇形统计图.
(1)这10天中,日最高气温的众数是
多少?
(2)计算这10天日最高气温的平均值.
解:(1)根据扇形统计图,35℃占的比例最大,因此日最高气温的众数是35℃.
(2)这10天日最高气温的平均值是:
32×10%+33×20%+34×20%+35×30%+36×20%=
34.3
℃
仿例:为了推动阳光体育运动的广泛开展,引导学生走向操场,走进大自然,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题.
(1)本次接受随机抽样调查的学生人数为
,
图①中m的值为
;
(2)求本次调查获取的样本数据的众数和中位数;
(3)根据样本数据,若学校计划购买200双运动鞋,
建议购买35号运动鞋多少双?
40
15
(2)∵在这组样本数据中,35出现了12次,出现次数最多,
∴这组样本的众数为35;
∵将这组样本数据按从小到大的顺序排列,其中处于中间的两个数都为36,
∴中位数为
=36;
(3)∵在40名学生中,鞋号为35的学生人数比例为30%,
∴由样本数据估计学校各年级中学生鞋号为35的人数比例约为30%,
则计划购买200双运动鞋,有200×30%=60双为35号.
1.数据2、7、3、7、5、3、7的众数是(
)
A.2
B.3
C.5
D.7
D
课堂练习
2.一位经销商计划进一批运动鞋,他到某地的一所学校里对八年级的100名男生的鞋号进行了调查,经销商最感兴趣的是这组鞋号的(
)
A.中位数
B.平均数
C.方差
D.众数
D
3.某班第一小组7名同学的毕业升学体育测试成
绩(满分30分)依次为:25,
23,25,23,27,30,
25,那么这组数据的中位数和众数分别是(
)
A.
23,25
B.
23,23
C.
25,23
D.
25,25
D
5.某次射击训练中,一小组的成绩如下表所示:
解:有4人的成绩为8环
若该小组的平均成绩为7.7环,则成绩为8环的有多少人?
4.一组数据3,4,9,x,它的平均数比它唯一的众数大1,则x=
.
4
6.对某校八年级随机抽取若干名学生进行体能测试,成绩记为1分,2分,3分,4分共4个等级,将调查结果绘制成如下条形统计图和扇形统计图.根据图中信息,这些学生的平均分数是
.
成绩频数条形统计图
成绩频数扇形统计图
2.95
7.某校八年级一班班长统计去年1~8月“校园文化”活动中全班同学的课外阅读数量(单位:本),绘制了如图所示的折线统计图,这组数据的中位数是______.
一班学生1~8月课外阅读数量折线统计图
58
8.某商店有200
L,215
L,185
L,180
L四种型号的冰箱,一段时间内共销售58台,其中四个型号分别售6台,30台,14台,8台,在研究电冰箱出售情况时,商店经理关心这组数据的平均数吗?他关心的是什么?
解:商店经理不关心这组数据的平均数,他关心的是众数,也就是哪种型号的电冰箱销量最好.
9.某乡镇企业生产部有技术工人15人,生产部为了合理制定产品的每月生产定额,统计了这15人某月的加工零件个数:
每人加工件数
540
450
300
240
210
120
人数
1
1
2
6
3
2
(1)写出这15人该月加工零件数的平均数、中位数和众数;
(2)假如生产部负责人把每位工人的月加工零件数定为260件,你认为这个定额是否合理,为什么?
解:(1)平均数:260(件),中位数:240(件),众数:240(件).
(2)不合理.因为表中数据显示,每月能完成260件的人数一共是4人,还有11人不能达到此定额,尽管260是平均数,但不利于调动多数员工的积极性.因为240既是中位数,又是众数,是大多数人能达到的定额,故定额为240较为合理.
10.三个生产日光灯管的厂家在广告中宣称,他们生产的日光灯管在正常情况下,灯管的使用寿命为12个月.工商部门为了检查他们宣传的真实性,从三个厂家各抽取11只日光灯管进行检测,灯管的使用寿命(单位:月)如下:
甲厂
7
8
9
9
9
11
13
14
16
17
19
乙厂
7
7
9
9
10
10
12
12
12
13
14
丙厂
7
7
8
8
8
12
13
14
15
16
17
试问:(1)这三个厂家的广告分别利用了统计中的哪一个特征数(平均数、中位数、众数)进行宣传?
(2)如果三种产品的售价一样,作为顾客的你会选购哪个厂家的产品?请说明理由.
解:(1)甲厂的广告利用了统计中的平均数.
乙厂的广告利用了统计中的众数.
丙厂的广告利用了统计中的中位数.
(2)选购甲厂的产品.理由是甲厂生产的灯管的使用寿命的平均数能较真实地反映灯管的使用寿命.或选用丙厂的产品.理由是丙厂生产的灯管的使用寿命有一半以上超过12个月.
从统计图分析数据的集中趋势
折线统计图
条形统计图
扇形统计图
总结新知
再
见
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
