华东师大版九年级数学上册第23章相似三角形的判定和性质复习课件(17张PPT)
文档属性
| 名称 | 华东师大版九年级数学上册第23章相似三角形的判定和性质复习课件(17张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 276.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览




文档简介
(共17张PPT)
用待定系数法求二次函数的解析式
文言文部分
相似三角形的判定和性质
专题复习课
回顾与反思
判定两个三角形相似的方法:
5.
4.
的两个三角形相似。
3.
1.定义:
的两个三角形相似。
2.平行三角形一边的直线定理:
所构成的三角形与原三角形相似.
三角对应相等,三边对应成比例
平行三角形一边的直线和其他
两边(或两边的延长线)相交,
的两个三角形相似。
的两个三角形相似。
三边对应成比例
两边对应成比例且夹角相等
两角分别相等
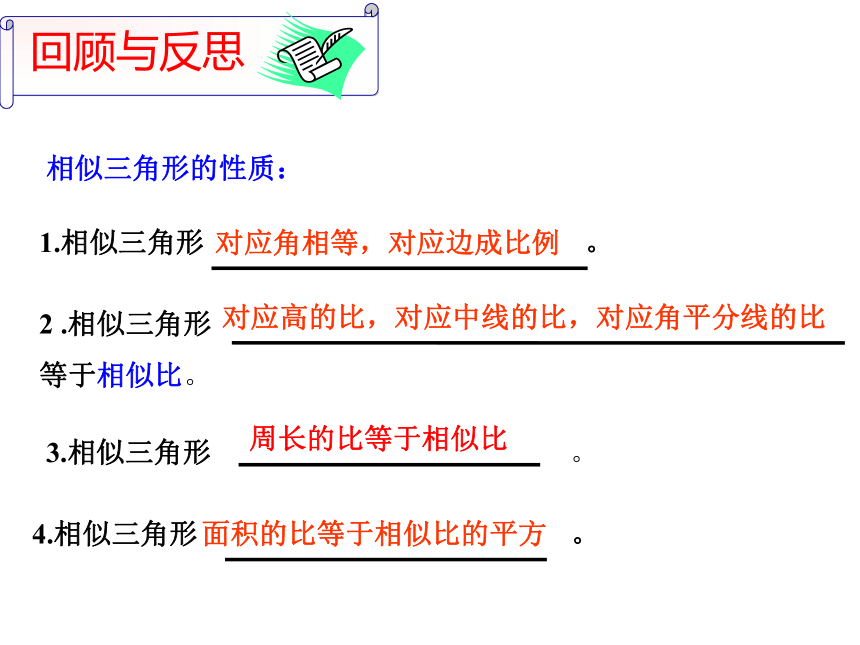
回顾与反思
相似三角形的性质:
1.相似三角形
。
2
.相似三角形
等于相似比。
4.相似三角形
。
对应角相等,对应边成比例
对应高的比,对应中线的比,对应角平分线的比
面积的比等于相似比的平方
3.相似三角形
。
周长的比等于相似比
A字型
X字型
公共边角型
双垂直型
相似中常用基本图形:
三等角型
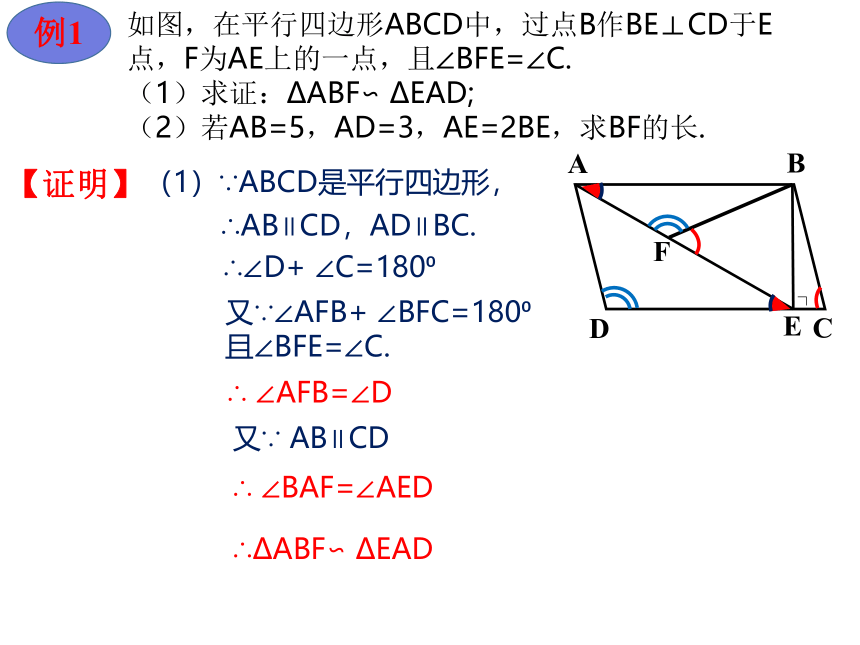
例1
如图,在平行四边形ABCD中,过点B作BE⊥CD于E点,F为AE上的一点,且∠BFE=∠C.
(1)求证:?ABF∽
?EAD;
(2)若AB=5,AD=3,AE=2BE,求BF的长.
∟
E
D
C
B
A
F
【证明】
(1)∵ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠D+
∠C=180?
又∵∠AFB+
∠BFC=180?
且∠BFE=∠C.
∴
∠AFB=∠D
又∵
AB∥CD
∴
∠BAF=∠AED
∴?ABF∽
?EAD
∟
E
D
C
B
A
F
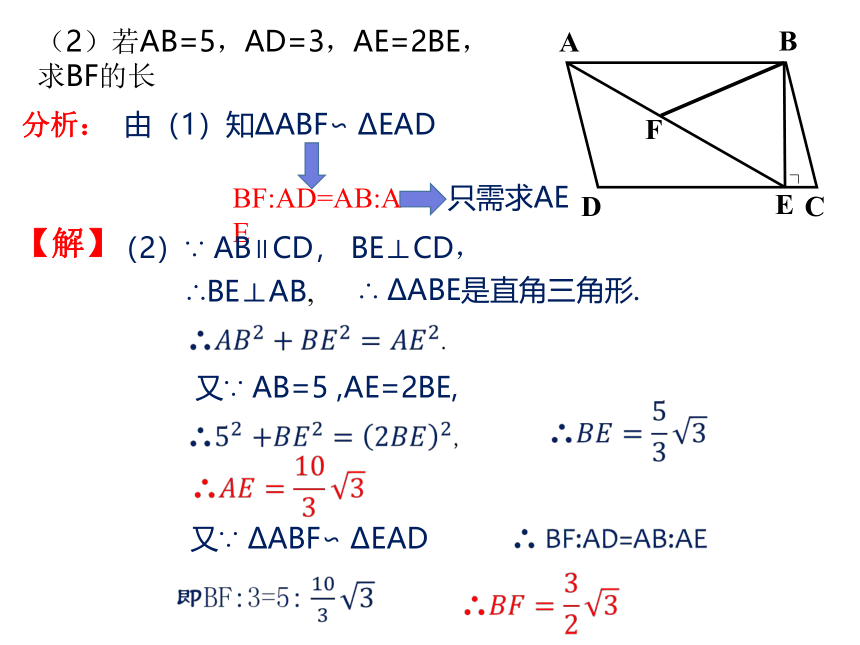
(2)若AB=5,AD=3,AE=2BE,求BF的长
分析:
由(1)知?ABF∽
?EAD
BF:AD=AB:AE
只需求AE
【解】
(2)∵
AB∥CD,
BE⊥CD,
∴BE⊥AB,
∴
?ABE是直角三角形.
又∵
AB=5
,AE=2BE,
又∵
?ABF∽
?EAD
助学微博
练习题:
1.(1)
△
ABC中,D、E分别是AB、AC上的点,且∠AED=
∠
B,那么△
AED
∽
△
ABC,从而
(2)
△
ABC中,AB的中点为D,AC的中点为E,连结DE,
则△
ADE与△
ABC的周长比为______.
2.如图,DE∥BC,
AD:DB=2:3,
则△
ADE和△
ABC
的面积比为___.
3.
已知三角形甲各边的比为3:4:6,
和它相似的三角形乙
的最大边为10cm,
则三角形乙的最短边为______cm.
AC
4:25
5
1:2
4.
如图,△ADE∽
△ACB,
则DE:BC=_____
。
5.
如图,D是△ABC一边BC
上一点,连接AD,使
△ABC
∽
△DBA的条件是(
).
A.
AC:BC=AD:BD
B.
AC:BC=AB:AD
C.
AB2=CD·BC
D.
AB2=BD·BC
6.
如图,D、E分别为△ABC
的AB、AC上
的点,且DE∥BC,∠DCB=
∠
A,
把每两个相似的三角形称为一组,那
么图中共有相似三角形_______组。
1:3
D
4
6.
D、E分别为△ABC
的AB、AC上的点,DE∥BC,
∠DCB=
∠
A,把每两个相似的三角形称为一组,
那么图中共有相似三角形_______组。
解:
∵
DE∥BC
∴∠ADE=
∠B,
∠EDC=∠DCB=∠A
①
∵
DE∥BC
∴△ADE
∽
△ABC
②
∵
∠A=
∠DCB,
∠ADE=
∠B
∴△ADE∽
△CBD
③
∵
△ADE
∽
△ABC
△ADE
∽
△CBD
∴
△ABC
∽
△CBD
④
∵
∠DCA=
∠DCE,
∠A=
∠EDC
∴
△ADC
∽
△DEC
1
当∠ACP=∠B,
A
C
B
P
2
或∠APC=∠ACB,
或AP:AC=AC:AB时,
如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,则需补上哪一个条件?
解:
△APC∽△ACB
.
例2
练习题:1.△在ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形.
E
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
E
E
这类题型的特征是有条件而无结论,要确定这些条件下可能出现的结论,解题思路是:从所给条件出发,通过分析、比较、猜想、寻求多种解法和结论,再进行证明.
小
结
相
似
三
角
形
2.性质
1.判定
对应高,中线,角平分线的比等于相似比
周长的比等于相似比
面积的比等于相似比的平方
谈谈本节课你的收获:
2.用预备定理(常用)
3.用判定定理(常用)
(1.AA
2.SAS
3.SSS)
1.定义(不常用)
作业:
A组:
第97页
第17题、第18题
1.如图,⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
(1)图中有全等三角形吗?找出来并证明.
(2)图中有相似三角形吗?找出来并证明.
(3)BD2=AD·DF吗?请说明理由.
B组:
B
C
A
Q
P
8
16
2cm/秒
4cm/秒
2.在?ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟?BPQ与?BAC相似?
用待定系数法求二次函数的解析式
文言文部分
相似三角形的判定和性质
专题复习课
回顾与反思
判定两个三角形相似的方法:
5.
4.
的两个三角形相似。
3.
1.定义:
的两个三角形相似。
2.平行三角形一边的直线定理:
所构成的三角形与原三角形相似.
三角对应相等,三边对应成比例
平行三角形一边的直线和其他
两边(或两边的延长线)相交,
的两个三角形相似。
的两个三角形相似。
三边对应成比例
两边对应成比例且夹角相等
两角分别相等
回顾与反思
相似三角形的性质:
1.相似三角形
。
2
.相似三角形
等于相似比。
4.相似三角形
。
对应角相等,对应边成比例
对应高的比,对应中线的比,对应角平分线的比
面积的比等于相似比的平方
3.相似三角形
。
周长的比等于相似比
A字型
X字型
公共边角型
双垂直型
相似中常用基本图形:
三等角型
例1
如图,在平行四边形ABCD中,过点B作BE⊥CD于E点,F为AE上的一点,且∠BFE=∠C.
(1)求证:?ABF∽
?EAD;
(2)若AB=5,AD=3,AE=2BE,求BF的长.
∟
E
D
C
B
A
F
【证明】
(1)∵ABCD是平行四边形,
∴AB∥CD,AD∥BC.
∴∠D+
∠C=180?
又∵∠AFB+
∠BFC=180?
且∠BFE=∠C.
∴
∠AFB=∠D
又∵
AB∥CD
∴
∠BAF=∠AED
∴?ABF∽
?EAD
∟
E
D
C
B
A
F
(2)若AB=5,AD=3,AE=2BE,求BF的长
分析:
由(1)知?ABF∽
?EAD
BF:AD=AB:AE
只需求AE
【解】
(2)∵
AB∥CD,
BE⊥CD,
∴BE⊥AB,
∴
?ABE是直角三角形.
又∵
AB=5
,AE=2BE,
又∵
?ABF∽
?EAD
助学微博
练习题:
1.(1)
△
ABC中,D、E分别是AB、AC上的点,且∠AED=
∠
B,那么△
AED
∽
△
ABC,从而
(2)
△
ABC中,AB的中点为D,AC的中点为E,连结DE,
则△
ADE与△
ABC的周长比为______.
2.如图,DE∥BC,
AD:DB=2:3,
则△
ADE和△
ABC
的面积比为___.
3.
已知三角形甲各边的比为3:4:6,
和它相似的三角形乙
的最大边为10cm,
则三角形乙的最短边为______cm.
AC
4:25
5
1:2
4.
如图,△ADE∽
△ACB,
则DE:BC=_____
。
5.
如图,D是△ABC一边BC
上一点,连接AD,使
△ABC
∽
△DBA的条件是(
).
A.
AC:BC=AD:BD
B.
AC:BC=AB:AD
C.
AB2=CD·BC
D.
AB2=BD·BC
6.
如图,D、E分别为△ABC
的AB、AC上
的点,且DE∥BC,∠DCB=
∠
A,
把每两个相似的三角形称为一组,那
么图中共有相似三角形_______组。
1:3
D
4
6.
D、E分别为△ABC
的AB、AC上的点,DE∥BC,
∠DCB=
∠
A,把每两个相似的三角形称为一组,
那么图中共有相似三角形_______组。
解:
∵
DE∥BC
∴∠ADE=
∠B,
∠EDC=∠DCB=∠A
①
∵
DE∥BC
∴△ADE
∽
△ABC
②
∵
∠A=
∠DCB,
∠ADE=
∠B
∴△ADE∽
△CBD
③
∵
△ADE
∽
△ABC
△ADE
∽
△CBD
∴
△ABC
∽
△CBD
④
∵
∠DCA=
∠DCE,
∠A=
∠EDC
∴
△ADC
∽
△DEC
1
当∠ACP=∠B,
A
C
B
P
2
或∠APC=∠ACB,
或AP:AC=AC:AB时,
如图点P是△ABC的AB边上的一点,要使△APC∽△ACB,则需补上哪一个条件?
解:
△APC∽△ACB
.
例2
练习题:1.△在ABC中,AB>AC,过AB上一点D作直线DE交另一边于E,使所得三角形与原三角形相似,画出满足条件的图形.
E
D
A
B
C
D
A
B
C
D
A
B
C
D
A
B
C
E
E
E
这类题型的特征是有条件而无结论,要确定这些条件下可能出现的结论,解题思路是:从所给条件出发,通过分析、比较、猜想、寻求多种解法和结论,再进行证明.
小
结
相
似
三
角
形
2.性质
1.判定
对应高,中线,角平分线的比等于相似比
周长的比等于相似比
面积的比等于相似比的平方
谈谈本节课你的收获:
2.用预备定理(常用)
3.用判定定理(常用)
(1.AA
2.SAS
3.SSS)
1.定义(不常用)
作业:
A组:
第97页
第17题、第18题
1.如图,⊿ABC是等边三角形,点D,E分别在BC,AC上,且BD=CE,AD与BE相交于点F.
(1)图中有全等三角形吗?找出来并证明.
(2)图中有相似三角形吗?找出来并证明.
(3)BD2=AD·DF吗?请说明理由.
B组:
B
C
A
Q
P
8
16
2cm/秒
4cm/秒
2.在?ABC中,AB=8cm,BC=16cm,点P从点A开始沿AB边向B点以2cm/秒的速度移动,点Q从点B开始沿BC向点C以4cm/秒的速度移动,如果P、Q分别从A、B同时出发,经几秒钟?BPQ与?BAC相似?
