沪科版数学八年级上册:13.1三角形中的边角关系课件(18张)
文档属性
| 名称 | 沪科版数学八年级上册:13.1三角形中的边角关系课件(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 130.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
问题1:
动手画一个三角形,并用自己的语言描述什么是三角形?
三角形定义:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形。
§13.1
三角形中的边角关系
(第1课时)
初中数学沪科版八年级上册第十三章《三角形的边角关系、命题与证明》
如图所示
1
(1)图中有____个三角形.
(2)∠1是哪个三角形的角?
(3)以AB为一条边的三角形
有____________________.
D
E
C
B
A
练一练
5
△ADE
,
△ACE
△ABC
,
△ABE
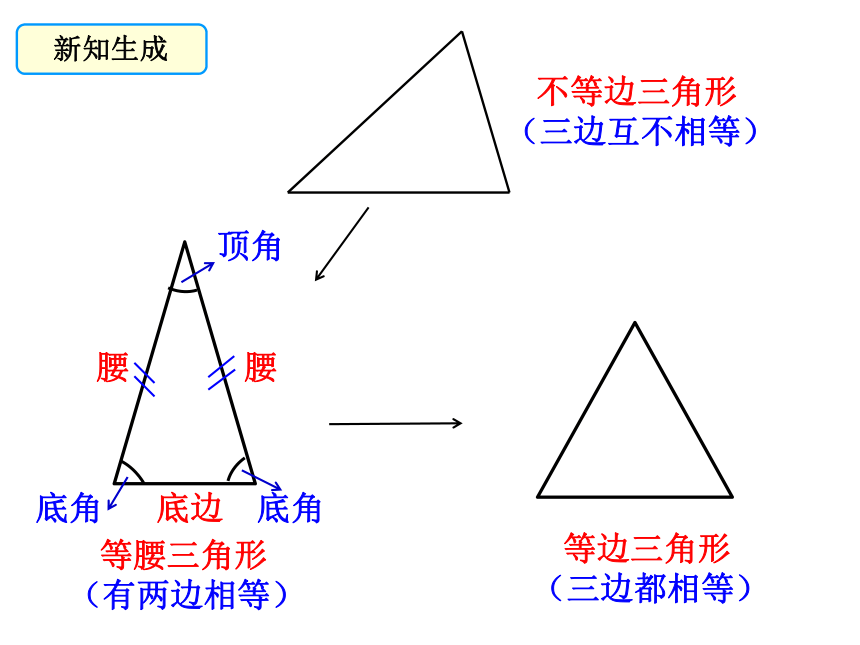
腰
腰
底边
顶角
底角
底角
不等边三角形
(三边互不相等)
等腰三角形
(有两边相等)
等边三角形
(三边都相等)
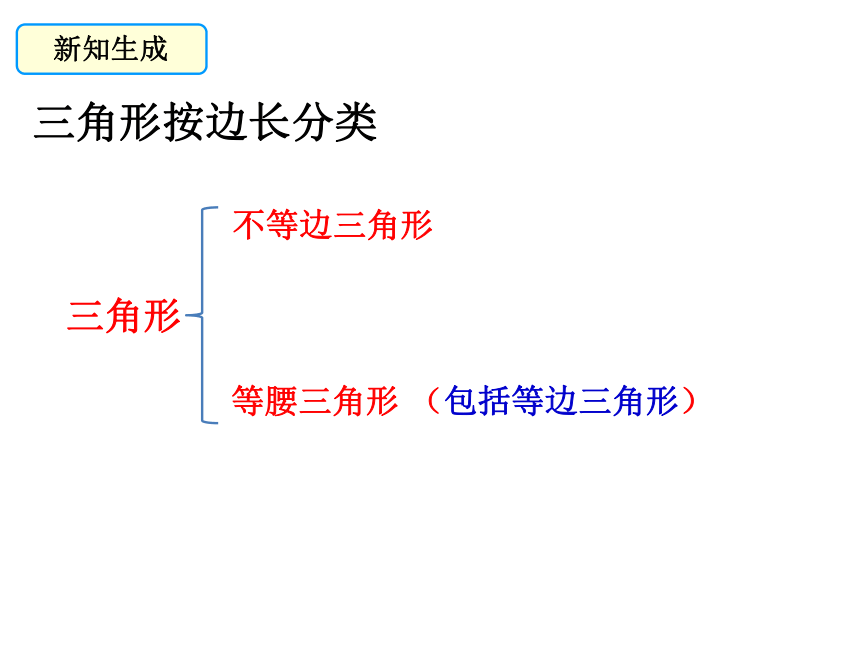
新知生成
三角形
不等边三角形
等腰三角形
三角形按边长分类
新知生成
(包括等边三角形)
问题3:
已知在△ABC中,AC=6cm,BC=8cm,求第三边AB的长.
小明家,小胖家,学校的位置如图所示,现在小明要从家出发去学校,他有几条路线可选择?
小明家
学校
小胖家
问题情境
A
B
C
小明家
学校
小胖家
小明家,小胖家,学校的位置如图所示,现在小明要从家出发去学校,他有几条路线可选择?
问题解决
三角形三边关系:
三角形中任意两边的和大于第三边
字母表示:
AB+AC>BC
AB+BC>AC
AC+BC>AB
新知生成
三角形中任意两边的差小于第三边
字母表示:
AB
—AC
<
BC
BC—AB
<
AC
AC
—
BC
<
AB
新知生成
1.
判断下列长度的三条线段能否拼成三角形?
为什么?
(1)3cm、4cm、
8cm;
(2)5cm、
11cm
、6cm;
(3)5cm、0.6dm、10cm.
练一练
问题3:
已知在△ABC中,AC=6cm,BC=8cm,则第三边AB的
取值范围是____________________.
8
-
6
<
AB
<
8+
6
问题解决
小结:两边之差<第三边<两边之和
a-b
<
x
<
a+b
2cm
<
AB
<
14cm
例1
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么
?
已知a,b,c是△ABC的三条边,
化简
|a-b-c|+|b-c-a|+|c+a-b|
能力提升
回忆本节课的学习,
你先后学到了哪些知识?有哪些收获或疑惑?
三角形
定义及其基本元素
边、顶点、角
按边分类
三边关系
原理
两点之间线段最短
内容
任意两边之和大于第三边
任意两边之差小于第三边
|a-b|(x为第三边)
应用
不等边三角形
等腰三角形(包括等边三角形)
1.课本69页练习1-3题.
(选做)思考
三角形的中的角有哪些关系?如何得到?
课下作业
问题1:
动手画一个三角形,并用自己的语言描述什么是三角形?
三角形定义:由不在同一条直线上的三条线段首尾依次相接所组成的封闭图形叫做三角形。
§13.1
三角形中的边角关系
(第1课时)
初中数学沪科版八年级上册第十三章《三角形的边角关系、命题与证明》
如图所示
1
(1)图中有____个三角形.
(2)∠1是哪个三角形的角?
(3)以AB为一条边的三角形
有____________________.
D
E
C
B
A
练一练
5
△ADE
,
△ACE
△ABC
,
△ABE
腰
腰
底边
顶角
底角
底角
不等边三角形
(三边互不相等)
等腰三角形
(有两边相等)
等边三角形
(三边都相等)
新知生成
三角形
不等边三角形
等腰三角形
三角形按边长分类
新知生成
(包括等边三角形)
问题3:
已知在△ABC中,AC=6cm,BC=8cm,求第三边AB的长.
小明家,小胖家,学校的位置如图所示,现在小明要从家出发去学校,他有几条路线可选择?
小明家
学校
小胖家
问题情境
A
B
C
小明家
学校
小胖家
小明家,小胖家,学校的位置如图所示,现在小明要从家出发去学校,他有几条路线可选择?
问题解决
三角形三边关系:
三角形中任意两边的和大于第三边
字母表示:
AB+AC>BC
AB+BC>AC
AC+BC>AB
新知生成
三角形中任意两边的差小于第三边
字母表示:
AB
—AC
<
BC
BC—AB
<
AC
AC
—
BC
<
AB
新知生成
1.
判断下列长度的三条线段能否拼成三角形?
为什么?
(1)3cm、4cm、
8cm;
(2)5cm、
11cm
、6cm;
(3)5cm、0.6dm、10cm.
练一练
问题3:
已知在△ABC中,AC=6cm,BC=8cm,则第三边AB的
取值范围是____________________.
8
-
6
<
AB
<
8+
6
问题解决
小结:两边之差<第三边<两边之和
a-b
<
x
<
a+b
2cm
<
AB
<
14cm
例1
用一条长为18cm的细绳围成一个等腰三角形.
(1)如果腰长是底边长的2倍,那么各边的长是多少?
(2)能围成有一边的长是4cm的等腰三角形吗?为什么
?
已知a,b,c是△ABC的三条边,
化简
|a-b-c|+|b-c-a|+|c+a-b|
能力提升
回忆本节课的学习,
你先后学到了哪些知识?有哪些收获或疑惑?
三角形
定义及其基本元素
边、顶点、角
按边分类
三边关系
原理
两点之间线段最短
内容
任意两边之和大于第三边
任意两边之差小于第三边
|a-b|
应用
不等边三角形
等腰三角形(包括等边三角形)
1.课本69页练习1-3题.
(选做)思考
三角形的中的角有哪些关系?如何得到?
课下作业
