人教版九年级数学上册: 24.4 弧长和扇形的面积(18张PPT)
文档属性
| 名称 | 人教版九年级数学上册: 24.4 弧长和扇形的面积(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 481.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 16:27:09 | ||
图片预览






文档简介
(共18张PPT)
第二十四章 圆
弧长和扇形的面积
问题1
制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算图1中所示的管道的展直长度L(结果取整数).
问题引入
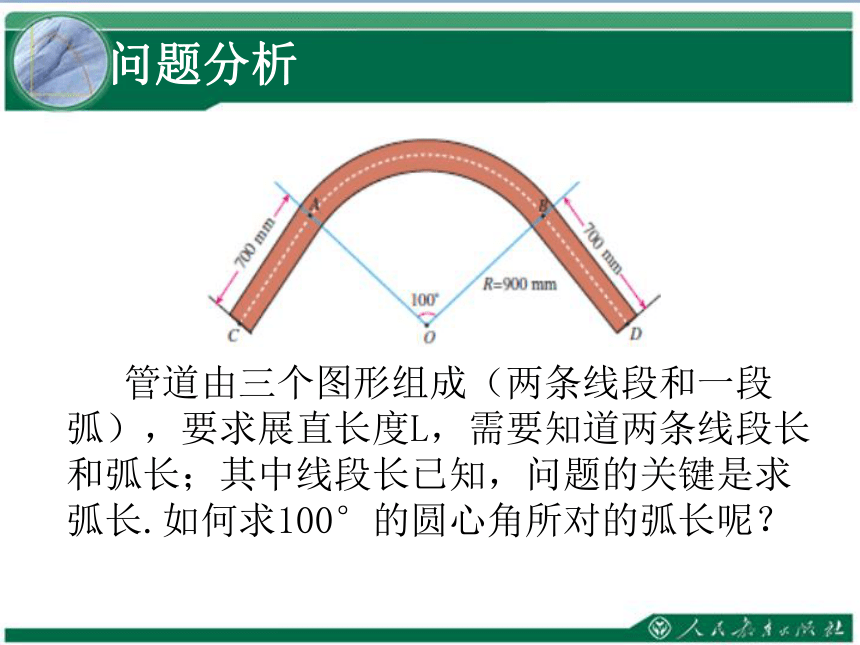
问题分析
管道由三个图形组成(两条线段和一段弧),要求展直长度L,需要知道两条线段长和弧长;其中线段长已知,问题的关键是求弧长.如何求100°的圆心角所对的弧长呢?
问题引导
①圆的周长可以看作是多少度的圆心角所对的弧长?
②180°的圆心角所对的弧长(半圆)是多少?
③90°的圆心角所对的弧长(半圆)是多少?
④在同圆或等圆中,每一个1°的圆心角所对的弧长有
怎样的关系?
⑤1°的圆心角所对的弧长是多少?
⑥n°的圆心角所对的弧长是多少?
360°
πR
相等
?
新知探究
1°的圆心角所对的弧长是
,n°的圆心角所对的弧长是1°的圆心角所对弧长的n倍,n°的圆心角所对的弧长为
(弧长公式)
注意:公式中n表示1°的圆心角的倍数,它是不带单位的,公式中,180也是不带单位的.
?
问题解决
问题2
我们现在已经知道如何计算弧长了,那么如何计算扇形面积呢?你能否类比研究弧长公式的方法推导出扇形面积的公式?
新知探究
问题引导
①180°的圆心角所对的扇形面积是多少?
②90°的圆心角所对的扇形面积是多少?
③60°的圆心角所对的扇形面积是多少?
④1°的圆心角所对的扇形面积是多少?
⑤n°的圆心角所对的扇形面积是多少?
新知探究
注意:公式中n表示1°的圆心角的倍数,它是不带单位的,公式中,360也是不带单位的.
1°的圆心角所对的扇形面积是圆面积的
,即
,则n°的圆心角所对的扇形面积为是圆面积
(扇形面积公式)
新知探究
新知探究
通过观察可以发现:
所以
(扇形面积公式)
巩固及应用
巩固及应用
巩固及应用
教科书113页练习1,2,3题.
练习:
巩固及应用
这一节课的收获…
1.弧长和扇形公式
2.弧长与圆周长、扇形面积与圆面积之间有什么联系?
弧长和扇形公式是什么?你是如何得到这两个公式的?如何运用?
归纳总结
教科书习题
24.4第2,4,6,8题.
复习巩固:第1,2,3题.
布置作业
目标检测
1.已知扇形的圆心角为70°,半径为1,则这个扇形的弧长是______.
2
.已知扇形的圆心角为50°,半径为4cm,则扇形的面积是________cm2.
3.如图,正△ABC内接于⊙O,边长为4
cm,求图中阴影部分的面积.
第二十四章 圆
弧长和扇形的面积
问题1
制造弯形管道时,经常要先按中心线计算“展直长度”,再下料,试计算图1中所示的管道的展直长度L(结果取整数).
问题引入
问题分析
管道由三个图形组成(两条线段和一段弧),要求展直长度L,需要知道两条线段长和弧长;其中线段长已知,问题的关键是求弧长.如何求100°的圆心角所对的弧长呢?
问题引导
①圆的周长可以看作是多少度的圆心角所对的弧长?
②180°的圆心角所对的弧长(半圆)是多少?
③90°的圆心角所对的弧长(半圆)是多少?
④在同圆或等圆中,每一个1°的圆心角所对的弧长有
怎样的关系?
⑤1°的圆心角所对的弧长是多少?
⑥n°的圆心角所对的弧长是多少?
360°
πR
相等
?
新知探究
1°的圆心角所对的弧长是
,n°的圆心角所对的弧长是1°的圆心角所对弧长的n倍,n°的圆心角所对的弧长为
(弧长公式)
注意:公式中n表示1°的圆心角的倍数,它是不带单位的,公式中,180也是不带单位的.
?
问题解决
问题2
我们现在已经知道如何计算弧长了,那么如何计算扇形面积呢?你能否类比研究弧长公式的方法推导出扇形面积的公式?
新知探究
问题引导
①180°的圆心角所对的扇形面积是多少?
②90°的圆心角所对的扇形面积是多少?
③60°的圆心角所对的扇形面积是多少?
④1°的圆心角所对的扇形面积是多少?
⑤n°的圆心角所对的扇形面积是多少?
新知探究
注意:公式中n表示1°的圆心角的倍数,它是不带单位的,公式中,360也是不带单位的.
1°的圆心角所对的扇形面积是圆面积的
,即
,则n°的圆心角所对的扇形面积为是圆面积
(扇形面积公式)
新知探究
新知探究
通过观察可以发现:
所以
(扇形面积公式)
巩固及应用
巩固及应用
巩固及应用
教科书113页练习1,2,3题.
练习:
巩固及应用
这一节课的收获…
1.弧长和扇形公式
2.弧长与圆周长、扇形面积与圆面积之间有什么联系?
弧长和扇形公式是什么?你是如何得到这两个公式的?如何运用?
归纳总结
教科书习题
24.4第2,4,6,8题.
复习巩固:第1,2,3题.
布置作业
目标检测
1.已知扇形的圆心角为70°,半径为1,则这个扇形的弧长是______.
2
.已知扇形的圆心角为50°,半径为4cm,则扇形的面积是________cm2.
3.如图,正△ABC内接于⊙O,边长为4
cm,求图中阴影部分的面积.
同课章节目录
