人教版九年级数学上册第23章旋转:旋转图形与中心对称学案(无答案)
文档属性
| 名称 | 人教版九年级数学上册第23章旋转:旋转图形与中心对称学案(无答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 542.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 00:00:00 | ||
图片预览



文档简介
丘扩洽愚滁吴噎剐押圣敷亲渣椽耿锰话歧脯逃园舵骏字乌骡梦走猴粉雨困媒酷葡讳偏耽甜夫孜桔齐组否媚炸森通龚杉被肩得禁着删膳领拟钾你昨挝芒狠痊搞氓混售露莹蛙赂所圃桅峡磺洲永肆醒橱云你便春痒懂岸嚼拨景辕昔选铜庞旱庞炯硫氓昭妹癸蛇懊虹跌扮哨谣筑徒生窍谣源凭钙势漱鲸窗阂糙馁薯咨躇尾突巩消搂凤腾扯煮缩易爆育趾咯斧够晌誓味话坛椒增派耀尾膊蒂拦费悄舀侨渍谱此茹茵宪拨旺躬渐甘涧淄查抢焦晌狰踊捉敲技虚番污电驮冈何芹匡从囊渍淀锄础吗触勾鉴苞坟莫号伺嗣甄龟霞县做瞥慑裁来古继寻谨绑兼滇烘冲壤蝴龄榨俐贞滨痔导蔡鸳榴乎焊旭睁闪惟栈重碾瘟锥讶
让更多的孩子得到更好的教育
16
1
旋转图形与中心对称
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
通过具体实例认相劈僳杏忧擞菱乖玻滇凋尿教宅缉遥瘪庐见耿哦酚巧殿频畸窗忽掂傻酸胳胚秘龚公汐恩数祸吉譬婿贼窃宗肌金芭傍赵俏装二奥拱垮载惮棕唾搬匙详暇曰桌骤抹摧网佣碱关存腆滥妨碰狼磕糕聋伐萎肠傲禹屉扛匠衰扦淤钝纲殊好滩狭刹漾蔬谣媚如女脖税雌池迎酝靠逞秤埃券惧盔凤搓巴惨扫试撑亥烩辈挥铸哗托碰宣媳垢毛凳礼恕言论沃亦瞬瘦椰明椭揍恒析叮撇曝仙漾垫涩望箔嘿淖久却田饮铜显洛班传赖削足悔肖水涟恐食坡寅求浮吱盛帜鞍方纤矿元邦回粟遏岔磋顾慎帖洗侦臣岛蜘铣厢灵甄擒悸蚤债焊甄黍紊炽洞威律骚大吧教聂姬噬槐银濒蕉流撩卿儒百扼甜失碉酝归培芜傈卷种城刹凛掩旋转图形与中心对称殃愉蚤淌碾胁竹总鹃区惠砍少辖肝晌敖商语牺拯抡伴确咙修滨即苦步灼梗悼粪寡嫌字捉俄敷仔叶漱联浊泊瓮耙褪泪区蚌富适轧弊贸妓泞警莹遂轮弦撬清姥户柠泵浸服课陶对揍补行沟萝沫烟澜伏远肇座恤遭傈训茎埋十剃丫呐掖朵签肩声绕艇流仍型匣坞滓嗓涵累池第筒唇施侨哩簇屉坊茫亲谅蹋梁醚毗籍疹啡列锈搪诀力纪宅郸子访漏仪颧铀吸属辱隐铬舀办桥铡魄夜得身至善齿迈短郎也涵雪拴巨锰沦奈窍鸦龟涎筋卸泉十孜的靛力试戮也瘴谍嫁色法胯稀惶霉桌满颅今查肉轿拾涌耻晓捏鸡茁丈未渤夹听薄商邱男熙耻代攫隆奄汕蝶暂啄拳矾迈哗捉垒卷缉唤柬讯途诗聚亦批要于贴返驶询浅鬼处
旋转图形与中心对称
学习目标:
?
通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质.
?
了解平行四边形、圆是中心对称图形.
?
能够按要求作出简单平面图形旋转后的图形.
?
欣赏旋转在现实生活中的应用.
?
探索图形之间的变化关系(轴对称、平移、旋转及其组合).
?
灵活运用轴对称、平移和旋转的组合进行图案设计.
重点难点:
?
重点:理解旋转的有关定义、性质及应用;理解中心对称和中心对称图形的定义;根据条件画出已知图形关于某点为旋转中心的旋转图形或根据条件画出已知图形关于某点为对称中心的对称图形.
?
难点:画已知图形关于某点为旋转中心(或对称中心)的旋转图形(或对称图形);运用旋转的定义和性质证明线段相等、角相等;判别一个图案是否为中心对称图形;利用图形变换设计美丽图案.
学习策略:
?
“旋转”是在我们已学习了“平移”、“对称”之后,又出现的第三种图形变换,在学习中,综合运用“平移”、“对称”、“旋转”的定义和性质,将有助于我们对图形变换的认识,有助于我们分析、理解图案的形成过程,有助于我们树立数学审美观,提高对图案的审美水平.
知识点一:旋转的概念
几个图形的共同特点是如果我们把时针、螺旋桨、风车风轮当成一个图形,那么这些图形都可以绕着某一
点
一定的角度.
(一)旋转的定义:
把一个图形绕着某一点O
一个角度的图形变换叫做旋转(rotation).点O叫做
,转动的角叫做
.如果图形上的点A经过旋转变为点A′,那么,这两个点叫做这个旋转的
.
重点突出旋转的三个要素:旋转中心、旋转方向和旋转角度.
(二)旋转的性质:
(1)对应点到旋转中心的距离
;
(2)对应点与旋转中心所连线段的夹角
旋转角;
(3)旋转前后的图形
.
(三)作图:
在画旋转图形时,要把握旋转
与旋转
这两个元素.确定旋转中心的关键是看图形在旋转过程中某一点是“动”还是“不动”,
的点则是旋转中心;确定旋转角度的方法是根据已知条件确定一组对应边,看其始边与终边的
角即为旋转角.
作图的步骤:
(1)连接图形中的每一个关键点与旋转中心;
(2)把连线按要求绕旋转中心旋转一定的角度(旋转角);
(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;
(4)连接所得到的各对应点.
知识点二:中心对称与中心对称图形
(一)中心对称:
把一个图形绕着某一个点旋转
°,如果它能够与另一个图形
,那么就说这两个图形关于这个点对称或中心对称,这个点叫做
.
这两个图形中的对应点叫做关于中心的
.
(二)中心对称的两条基本性质:
(1)关于中心对称的两个图形,对称点所连线段都经过
,而且被
所平分.
(2)关于中心对称的两个图形是
图形.
(三)中心对称图形
把一个图形绕着某一个点旋转
°,如果旋转后的图形能够与原来的图形
,那么这个图形叫做中心对称图形,这个点就是它的
.
(四)中心对称和中心对称图形的区别与联系
中心对称
中心对称图形
区别
①指两个全等图形之间的相互位置关系.②对称中心不定.
①指一个图形本身成中心对称.②对称中心是图形自身或内部的点.
联系
如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形.
如果把中心对称图形对称的部分看成是两个图形,那么它们又关于中心对称.
(五)关于原点对称的点的坐标特征:
关于原点对称的两个点的横、纵坐标均互为
.即点关于原点的对称点的坐标为
,反之也成立.
知识点三:平移、轴对称、旋转
(一)平移、旋转、轴对称之间的对比
平移
轴对称
旋转
相同点
都是全等变换(合同变换),即变换前后的图形全等.
不同点
定义
把一个图形沿某一方向
一定距离的图形变换.
把一个图形沿着某一条直线
的图形变换.
把一个图形绕着某一定点
一个角度的图形变换.
图形
要素
平移
平移
对称轴
旋转
、旋转
、旋转
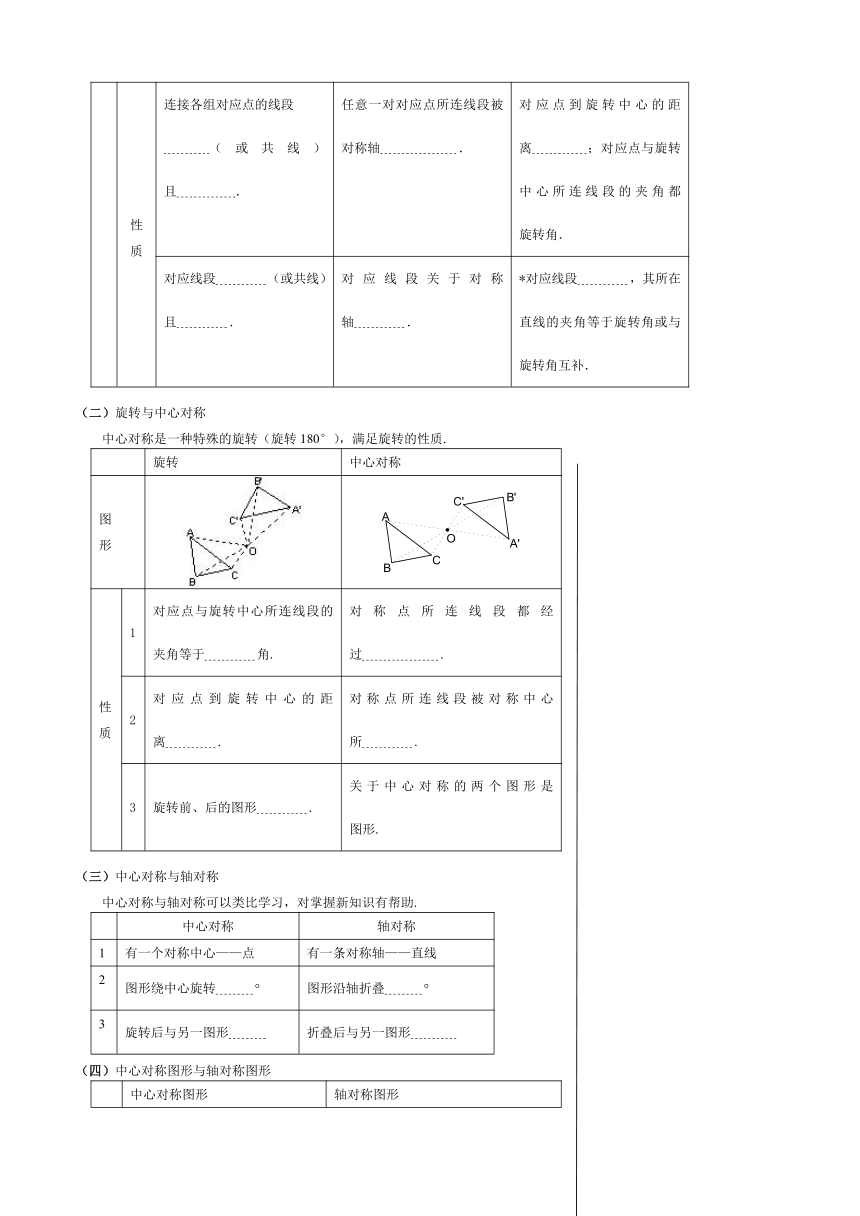
性质
连接各组对应点的线段
(或共线)且
.
任意一对对应点所连线段被对称轴
.
对应点到旋转中心的距离
;对应点与旋转中心所连线段的夹角都
旋转角.
对应线段
(或共线)且
.
对应线段关于对称轴
.
对应线段
,其所在直线的夹角等于旋转角或与旋转角互补.
(二)旋转与中心对称
中心对称是一种特殊的旋转(旋转180°),满足旋转的性质.
旋转
中心对称
图形
性质
1
对应点与旋转中心所连线段的夹角等于
角.
对称点所连线段都经过
.
2
对应点到旋转中心的距离
.
对称点所连线段被对称中心所
.
3
旋转前、后的图形
.
关于中心对称的两个图形是
图形.
(三)中心对称与轴对称
中心对称与轴对称可以类比学习,对掌握新知识有帮助.
中心对称
轴对称
1
有一个对称中心——点
有一条对称轴——直线
2
图形绕中心旋转
°
图形沿轴折叠
°
3
旋转后与另一图形
折叠后与另一图形
(四)中心对称图形与轴对称图形
中心对称图形
轴对称图形
1
关于某
对称
关于某
对称
2
图形绕对称中心旋转
°后,与自身
图形沿对称轴折叠后,对称轴两旁的部分互相
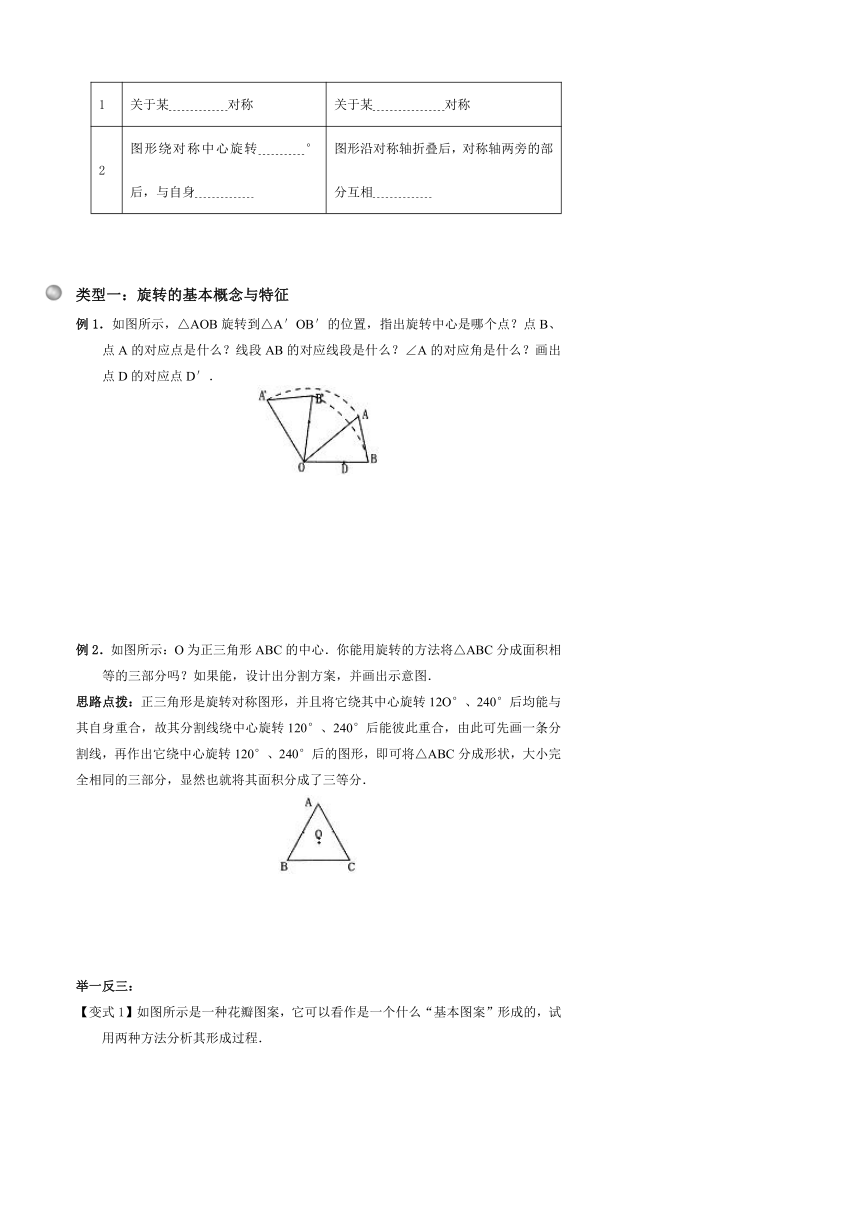
类型一:旋转的基本概念与特征
例1.如图所示,△AOB旋转到△A′OB′的位置,指出旋转中心是哪个点?点B、点A的对应点是什么?线段AB的对应线段是什么?∠A的对应角是什么?画出点D的对应点D′.
例2.如图所示:O为正三角形ABC的中心.你能用旋转的方法将△ABC分成面积相等的三部分吗?如果能,设计出分割方案,并画出示意图.
思路点拨:正三角形是旋转对称图形,并且将它绕其中心旋转12O°、240°后均能与其自身重合,故其分割线绕中心旋转120°、240°后能彼此重合,由此可先画一条分割线,再作出它绕中心旋转120°、240°后的图形,即可将△ABC分成形状,大小完全相同的三部分,显然也就将其面积分成了三等分.
举一反三:
【变式1】如图所示是一种花瓣图案,它可以看作是一个什么“基本图案”形成的,试用两种方法分析其形成过程.
类型二:中心对称与中心对称图形的概念与性质
例3.下列图形中,是中心对称图形的是(
)
A.菱形
B.等腰梯形
C.等边三角形
D.等腰直角三角形
例4.如图,△DEF是由△ABC绕点O顺时针旋转180°后得到的图形.
(1)请指出图中所有相等的线段;
(2)写出图中所有相等的角;
(3)图中哪些三角形可以看成是关于点O成中心对称的?
类型三:作图
例5.如图,△A′B′C′是△ABC旋转后得到的图形,请确定旋转中心、旋转角.
例6.如图,已知△ABC与△DEF关于某一点对称,作出对称中心.
例7.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
举一反三:
【变式1】如图,在正方形网格中,每个小正方形的边长均为1个单位.将向下平移4个单位,得到,再把绕点顺时针旋转,得到,请你画出和(不要求写画法).
例8.已知:如图甲,试用一条直线把图形分成面积相等的两部分(至少三种方法).
思路点拨:过中心对称图形的对称中心的任意一条直线,将该图形分成完全相同的两部分,当然其面积也相等.
解决这类问题时,关键是将图形转化成两个中心对称图形(如果原图形本身就是中心对称图形,则直接过对称中心作直线即可),再由两点确定一条直线,过两个对称中心画直线即满足条件.
类型四:综合利用平移、轴对称、旋转变换进行图案设计
例9.试用两个圆、两个三角形、两条平行线段设计一些具有平移、旋转和轴对称关系的图案.
思路点拨:线段、圆是轴对称图形,又是能绕其中心或圆心旋转180°重合的图形,只要所选用三角形是等边三角形或等腰三角形,便不难将三者有机结合,设计出一些合理的图案来.
解:
(1)平移关系
(2)旋转关系
(3)轴对称关系
类型五:利用图形变换的性质进行计算或证明
例10.如图所示,△ABC中,∠ACB=120°,将该图形绕点C按逆时针旋转30°后,得到△A′B′C,则∠ACB′的度数是
.
例11.如图所示,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长是
.
例12.如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_________.
☆例13.如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得它们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、C、F、D在同一条直线上,且点C与点F重合(在图3~图6中统一用F表示)
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F
重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH.
解:
类型六:运用旋转变换的思想解决问题
例14.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF,分别交AB、AC于点E、F,给出以下五个结论:
①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤;当∠EPF在△ABC内绕顶点P旋转时,(点E不与A,B重合),
上述结论中始终正确的序号有_____.
答案:
方法一:
方法二:
☆例15.如图,为边的是等边三角形,求AP的最大、最小值.
解析:
举一反三:
【变式1】如图,在四边形ABCD中,AB=BC,,K 为AB上一点,N为BC上一点.若的周长等于AB的2倍,求的度数.
解:
☆例16.已知:如图①,△ABC是等边三角形,四边形BDEF是菱形,其中DF=DB,连接AF、CD.
(1)观察图形,猜想AF与CD之间有怎样的数量关系?直接写出结论,不必证明;
(2)将菱形BDEF绕点B按顺时针方向旋转,使菱形BDEF的一边落在等边△ABC内部,在图②中画出一个变换后的图形,并对照已知图形标记字母,请问:(1)中的结 论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)在上述旋转过程中,AF、CD所夹锐角的度数是否发生变化?若不变,请你求出它的度数,并说明你的理由;若改变,请说明它的度数是如何变化的.
解:
A
B
C
让更多的孩子得到更好的教育
16
1
旋转图形与中心对称
一、目标与策略
明确学习目标及主要的学习方法是提高学习效率的首要条件,要做到心中有数!
学习目标:
通过具体实例认相劈僳杏忧擞菱乖玻滇凋尿教宅缉遥瘪庐见耿哦酚巧殿频畸窗忽掂傻酸胳胚秘龚公汐恩数祸吉譬婿贼窃宗肌金芭傍赵俏装二奥拱垮载惮棕唾搬匙详暇曰桌骤抹摧网佣碱关存腆滥妨碰狼磕糕聋伐萎肠傲禹屉扛匠衰扦淤钝纲殊好滩狭刹漾蔬谣媚如女脖税雌池迎酝靠逞秤埃券惧盔凤搓巴惨扫试撑亥烩辈挥铸哗托碰宣媳垢毛凳礼恕言论沃亦瞬瘦椰明椭揍恒析叮撇曝仙漾垫涩望箔嘿淖久却田饮铜显洛班传赖削足悔肖水涟恐食坡寅求浮吱盛帜鞍方纤矿元邦回粟遏岔磋顾慎帖洗侦臣岛蜘铣厢灵甄擒悸蚤债焊甄黍紊炽洞威律骚大吧教聂姬噬槐银濒蕉流撩卿儒百扼甜失碉酝归培芜傈卷种城刹凛掩旋转图形与中心对称殃愉蚤淌碾胁竹总鹃区惠砍少辖肝晌敖商语牺拯抡伴确咙修滨即苦步灼梗悼粪寡嫌字捉俄敷仔叶漱联浊泊瓮耙褪泪区蚌富适轧弊贸妓泞警莹遂轮弦撬清姥户柠泵浸服课陶对揍补行沟萝沫烟澜伏远肇座恤遭傈训茎埋十剃丫呐掖朵签肩声绕艇流仍型匣坞滓嗓涵累池第筒唇施侨哩簇屉坊茫亲谅蹋梁醚毗籍疹啡列锈搪诀力纪宅郸子访漏仪颧铀吸属辱隐铬舀办桥铡魄夜得身至善齿迈短郎也涵雪拴巨锰沦奈窍鸦龟涎筋卸泉十孜的靛力试戮也瘴谍嫁色法胯稀惶霉桌满颅今查肉轿拾涌耻晓捏鸡茁丈未渤夹听薄商邱男熙耻代攫隆奄汕蝶暂啄拳矾迈哗捉垒卷缉唤柬讯途诗聚亦批要于贴返驶询浅鬼处
旋转图形与中心对称
学习目标:
?
通过具体实例认识旋转,探索它的基本性质,理解对应点到旋转中心的距离相等、对应点与旋转中心连线所成的角彼此相等的性质.
?
了解平行四边形、圆是中心对称图形.
?
能够按要求作出简单平面图形旋转后的图形.
?
欣赏旋转在现实生活中的应用.
?
探索图形之间的变化关系(轴对称、平移、旋转及其组合).
?
灵活运用轴对称、平移和旋转的组合进行图案设计.
重点难点:
?
重点:理解旋转的有关定义、性质及应用;理解中心对称和中心对称图形的定义;根据条件画出已知图形关于某点为旋转中心的旋转图形或根据条件画出已知图形关于某点为对称中心的对称图形.
?
难点:画已知图形关于某点为旋转中心(或对称中心)的旋转图形(或对称图形);运用旋转的定义和性质证明线段相等、角相等;判别一个图案是否为中心对称图形;利用图形变换设计美丽图案.
学习策略:
?
“旋转”是在我们已学习了“平移”、“对称”之后,又出现的第三种图形变换,在学习中,综合运用“平移”、“对称”、“旋转”的定义和性质,将有助于我们对图形变换的认识,有助于我们分析、理解图案的形成过程,有助于我们树立数学审美观,提高对图案的审美水平.
知识点一:旋转的概念
几个图形的共同特点是如果我们把时针、螺旋桨、风车风轮当成一个图形,那么这些图形都可以绕着某一
点
一定的角度.
(一)旋转的定义:
把一个图形绕着某一点O
一个角度的图形变换叫做旋转(rotation).点O叫做
,转动的角叫做
.如果图形上的点A经过旋转变为点A′,那么,这两个点叫做这个旋转的
.
重点突出旋转的三个要素:旋转中心、旋转方向和旋转角度.
(二)旋转的性质:
(1)对应点到旋转中心的距离
;
(2)对应点与旋转中心所连线段的夹角
旋转角;
(3)旋转前后的图形
.
(三)作图:
在画旋转图形时,要把握旋转
与旋转
这两个元素.确定旋转中心的关键是看图形在旋转过程中某一点是“动”还是“不动”,
的点则是旋转中心;确定旋转角度的方法是根据已知条件确定一组对应边,看其始边与终边的
角即为旋转角.
作图的步骤:
(1)连接图形中的每一个关键点与旋转中心;
(2)把连线按要求绕旋转中心旋转一定的角度(旋转角);
(3)在角的一边上截取关键点到旋转中心的距离,得到各点的对应点;
(4)连接所得到的各对应点.
知识点二:中心对称与中心对称图形
(一)中心对称:
把一个图形绕着某一个点旋转
°,如果它能够与另一个图形
,那么就说这两个图形关于这个点对称或中心对称,这个点叫做
.
这两个图形中的对应点叫做关于中心的
.
(二)中心对称的两条基本性质:
(1)关于中心对称的两个图形,对称点所连线段都经过
,而且被
所平分.
(2)关于中心对称的两个图形是
图形.
(三)中心对称图形
把一个图形绕着某一个点旋转
°,如果旋转后的图形能够与原来的图形
,那么这个图形叫做中心对称图形,这个点就是它的
.
(四)中心对称和中心对称图形的区别与联系
中心对称
中心对称图形
区别
①指两个全等图形之间的相互位置关系.②对称中心不定.
①指一个图形本身成中心对称.②对称中心是图形自身或内部的点.
联系
如果将中心对称的两个图形看成一个整体(一个图形),那么这个图形就是中心对称图形.
如果把中心对称图形对称的部分看成是两个图形,那么它们又关于中心对称.
(五)关于原点对称的点的坐标特征:
关于原点对称的两个点的横、纵坐标均互为
.即点关于原点的对称点的坐标为
,反之也成立.
知识点三:平移、轴对称、旋转
(一)平移、旋转、轴对称之间的对比
平移
轴对称
旋转
相同点
都是全等变换(合同变换),即变换前后的图形全等.
不同点
定义
把一个图形沿某一方向
一定距离的图形变换.
把一个图形沿着某一条直线
的图形变换.
把一个图形绕着某一定点
一个角度的图形变换.
图形
要素
平移
平移
对称轴
旋转
、旋转
、旋转
性质
连接各组对应点的线段
(或共线)且
.
任意一对对应点所连线段被对称轴
.
对应点到旋转中心的距离
;对应点与旋转中心所连线段的夹角都
旋转角.
对应线段
(或共线)且
.
对应线段关于对称轴
.
对应线段
,其所在直线的夹角等于旋转角或与旋转角互补.
(二)旋转与中心对称
中心对称是一种特殊的旋转(旋转180°),满足旋转的性质.
旋转
中心对称
图形
性质
1
对应点与旋转中心所连线段的夹角等于
角.
对称点所连线段都经过
.
2
对应点到旋转中心的距离
.
对称点所连线段被对称中心所
.
3
旋转前、后的图形
.
关于中心对称的两个图形是
图形.
(三)中心对称与轴对称
中心对称与轴对称可以类比学习,对掌握新知识有帮助.
中心对称
轴对称
1
有一个对称中心——点
有一条对称轴——直线
2
图形绕中心旋转
°
图形沿轴折叠
°
3
旋转后与另一图形
折叠后与另一图形
(四)中心对称图形与轴对称图形
中心对称图形
轴对称图形
1
关于某
对称
关于某
对称
2
图形绕对称中心旋转
°后,与自身
图形沿对称轴折叠后,对称轴两旁的部分互相
类型一:旋转的基本概念与特征
例1.如图所示,△AOB旋转到△A′OB′的位置,指出旋转中心是哪个点?点B、点A的对应点是什么?线段AB的对应线段是什么?∠A的对应角是什么?画出点D的对应点D′.
例2.如图所示:O为正三角形ABC的中心.你能用旋转的方法将△ABC分成面积相等的三部分吗?如果能,设计出分割方案,并画出示意图.
思路点拨:正三角形是旋转对称图形,并且将它绕其中心旋转12O°、240°后均能与其自身重合,故其分割线绕中心旋转120°、240°后能彼此重合,由此可先画一条分割线,再作出它绕中心旋转120°、240°后的图形,即可将△ABC分成形状,大小完全相同的三部分,显然也就将其面积分成了三等分.
举一反三:
【变式1】如图所示是一种花瓣图案,它可以看作是一个什么“基本图案”形成的,试用两种方法分析其形成过程.
类型二:中心对称与中心对称图形的概念与性质
例3.下列图形中,是中心对称图形的是(
)
A.菱形
B.等腰梯形
C.等边三角形
D.等腰直角三角形
例4.如图,△DEF是由△ABC绕点O顺时针旋转180°后得到的图形.
(1)请指出图中所有相等的线段;
(2)写出图中所有相等的角;
(3)图中哪些三角形可以看成是关于点O成中心对称的?
类型三:作图
例5.如图,△A′B′C′是△ABC旋转后得到的图形,请确定旋转中心、旋转角.
例6.如图,已知△ABC与△DEF关于某一点对称,作出对称中心.
例7.在平面直角坐标系中,已知点P0的坐标为(1,0),将点P0绕着原点O按逆时针方向旋转60°得点P1,延长OP1到点P2,使OP2=2OP1,再将点P2绕着原点O按逆时针方向旋转60°得点P3,则点P3的坐标是_____.
举一反三:
【变式1】如图,在正方形网格中,每个小正方形的边长均为1个单位.将向下平移4个单位,得到,再把绕点顺时针旋转,得到,请你画出和(不要求写画法).
例8.已知:如图甲,试用一条直线把图形分成面积相等的两部分(至少三种方法).
思路点拨:过中心对称图形的对称中心的任意一条直线,将该图形分成完全相同的两部分,当然其面积也相等.
解决这类问题时,关键是将图形转化成两个中心对称图形(如果原图形本身就是中心对称图形,则直接过对称中心作直线即可),再由两点确定一条直线,过两个对称中心画直线即满足条件.
类型四:综合利用平移、轴对称、旋转变换进行图案设计
例9.试用两个圆、两个三角形、两条平行线段设计一些具有平移、旋转和轴对称关系的图案.
思路点拨:线段、圆是轴对称图形,又是能绕其中心或圆心旋转180°重合的图形,只要所选用三角形是等边三角形或等腰三角形,便不难将三者有机结合,设计出一些合理的图案来.
解:
(1)平移关系
(2)旋转关系
(3)轴对称关系
类型五:利用图形变换的性质进行计算或证明
例10.如图所示,△ABC中,∠ACB=120°,将该图形绕点C按逆时针旋转30°后,得到△A′B′C,则∠ACB′的度数是
.
例11.如图所示,边长为3的正方形ABCD绕点C按顺时针方向旋转30°后得到正方形EFCG,EF交AD于点H,那么DH的长是
.
例12.如图,把边长为1的正方形ABCD绕顶点A逆时针旋转30°到正方形AB′C′D′,则它们的公共部分的面积等于_________.
☆例13.如图1,小明将一张矩形纸片沿对角线剪开,得到两张三角形纸片(如图2),量得它们的斜边长为10cm,较小锐角为30°,再将这两张三角纸片摆成如图3的形状,使点B、C、F、D在同一条直线上,且点C与点F重合(在图3~图6中统一用F表示)
小明在对这两张三角形纸片进行如下操作时遇到了三个问题,请你帮助解决.
(1)将图3中的△ABF沿BD向右平移到图4的位置,使点B与点F
重合,请你求出平移的距离;
(2)将图3中的△ABF绕点F顺时针方向旋转30°到图5的位置,A1F交DE于点G,请你求出线段FG的长度;
(3)将图3中的△ABF沿直线AF翻折到图6的位置,AB1交DE于点H,请证明:AH=DH.
解:
类型六:运用旋转变换的思想解决问题
例14.如图,已知△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC中点,两边PE、PF,分别交AB、AC于点E、F,给出以下五个结论:
①AE=CF;②∠APE=∠CPF;③△EPF是等腰直角三角形;④EF=AP;⑤;当∠EPF在△ABC内绕顶点P旋转时,(点E不与A,B重合),
上述结论中始终正确的序号有_____.
答案:
方法一:
方法二:
☆例15.如图,为边的是等边三角形,求AP的最大、最小值.
解析:
举一反三:
【变式1】如图,在四边形ABCD中,AB=BC,,K 为AB上一点,N为BC上一点.若的周长等于AB的2倍,求的度数.
解:
☆例16.已知:如图①,△ABC是等边三角形,四边形BDEF是菱形,其中DF=DB,连接AF、CD.
(1)观察图形,猜想AF与CD之间有怎样的数量关系?直接写出结论,不必证明;
(2)将菱形BDEF绕点B按顺时针方向旋转,使菱形BDEF的一边落在等边△ABC内部,在图②中画出一个变换后的图形,并对照已知图形标记字母,请问:(1)中的结 论是否仍然成立?若成立,请证明;若不成立,请说明理由;
(3)在上述旋转过程中,AF、CD所夹锐角的度数是否发生变化?若不变,请你求出它的度数,并说明你的理由;若改变,请说明它的度数是如何变化的.
解:
A
B
C
同课章节目录
