人教版七年级上册数学1.5.1乘方课件(23张)
文档属性
| 名称 | 人教版七年级上册数学1.5.1乘方课件(23张) |

|
|
| 格式 | zip | ||
| 文件大小 | 862.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 16:45:44 | ||
图片预览






文档简介
(共23张PPT)
§1.5.1
乘方
这种求
个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂。
在
中,
叫做底数,
叫做指数。
幂
读作
的
次方,也可以读作
的
次幂。
指数
因数的个数
底数
因数
相同因数
个相同的因数
相乘,即
我们把它记作
n个a相乘
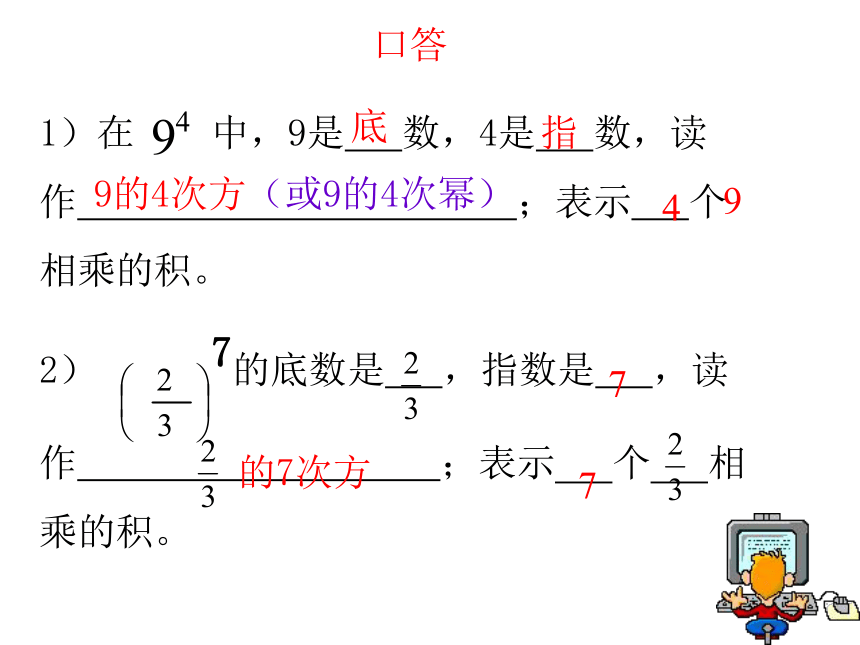
口答
1)在
中,9是
数,4是
数,读作
;表示
个
相乘的积。
2)
7的底数是
,指数是
,读
作
;表示
个
相乘的积。
7
的7次方
底
指
9的4次方(或9的4次幂)
4
9
7
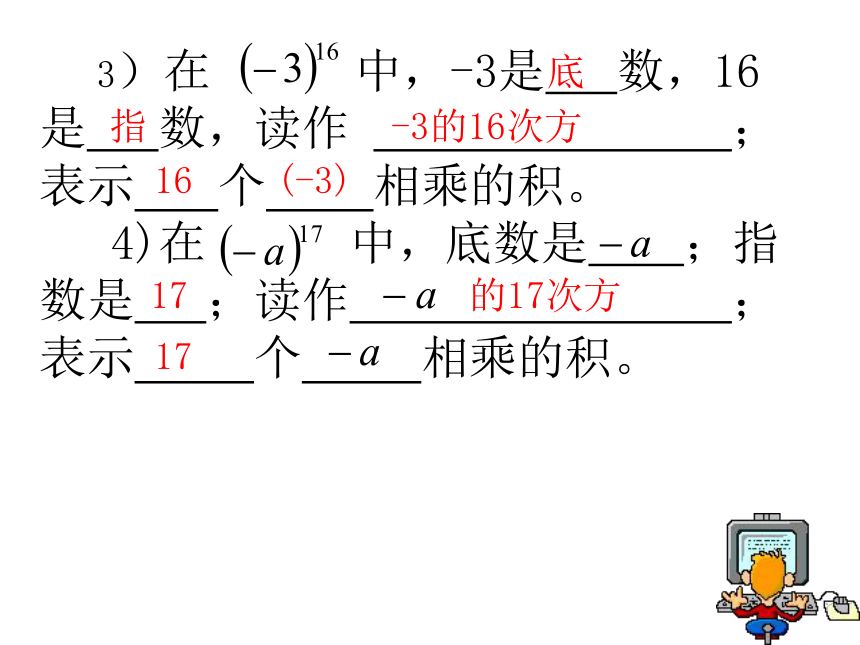
3)在
中,-3是
数,16是
数,读作
;表示
个
相乘的积。
4)在
中,底数是
;指数是
;读作
;表示
个
相乘的积。
底
指
-3的16次方
17
的17次方
16
(-3)
17
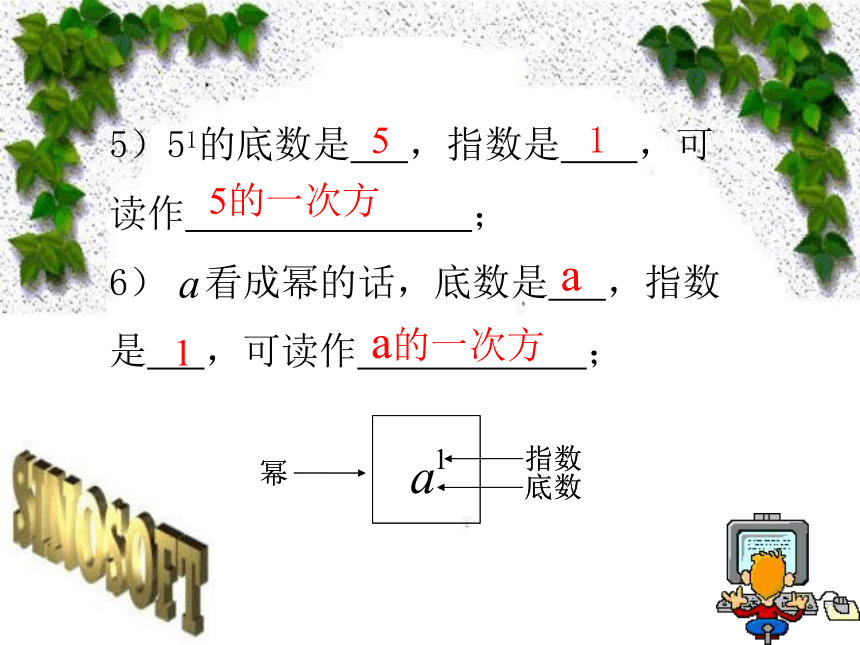
5)51的底数是
,指数是
,可读作
;
6)
看成幂的话,底数是
,指数是
,可读作
;
幂
指数
底数
5
1
5的一次方
1
a的一次方
1
a
幂
指数
底数
a
课堂练习
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1=
;
2、3×3×3×3×3=
;
3、(-3)×(-3)×(-3)×(-3)=
;
4、
=
;
二、把下列乘方写成乘法的形式:
1、
=
;
2、
=
;
3、
=
;
思考:用乘方式子怎么表示
的相反数?
-
答案:
课堂练习
判断下列各题是否正确:
(
)①
;
(
)②
;
(
)③
;
(
)④
对
错
错
错
解决下列问题,你能从中发现什么?
(1)
32与23有什么区别?各等于什么?
(2)
-34和(-3)
4有什么区别?各等于什么?
(3)2×32和(2×3)2
有什么区别?
(4)
有什么区别?各等于什么?
交流与思考
解决下列问题,你能从中发现什么?
(1)
32与23有什么区别?各等于什么?
(2)
-34和(-3)
4有什么区别?各等于什么?
答:(1)
32表示3的2次幂;而23表示2的3次幂,
它们的结果分别是9和8.
(2)-34表示4个3相乘的积的相反数或3的4次幂的相反数,结果是-81
;而(-3)
4则表示4个(-3)相乘的积或(-3)的4次幂,结果是81.
交流与思考
解决下列问题,你能从中发现什么?
(3)2×32和(2×3)2
有什么区别?
(4)
有什么区别?各等于什么?
答:
(3)
2×32表示
2与3的平方之积,等于18;
而(2×3)2表示2与3的积的平方,等于36.
交流与思考
例1计算:
解:
如果幂的底数是正数,那么这个幂有可能是负数吗?
不可能!正数的任何次幂是都是正数
从例1,你发现负数的幂的正负有什么规律?
当指数是
数时,负数的幂是
数;
当指数是
数时,负数的幂是
数。
幂的性质:
负数的奇次幂是负数,负数的
偶次幂是正数;
正数的任何次幂都是正数;
0
的任何正整数次幂是
0
。
口答
1)
是
(填“正”或“负”)数;
2)
是
(填“正”或“负”)数;
3)
=
;
4)
=
;
1
1
正
负
课堂练习
(课本第43-44页,练习第2题)
计算:
(1)
(-1)10
(2)(-1)7
(3)83
(4)
(-5)3
(5)(0.1)3
(6)(
)4
(7)(-10)4
(8)(-10)5
珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰?
≈
≈
想一想
想一想
若对折30次,算式中有几个2相乘?
对折2次可裁成4张,即2×2=22张;
对折3次可裁成8张,即2×2×2=23张;
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
动手做一做
解:
对折30次后的厚度为
折叠30次后的厚度超过珠穆朗玛峰
这种求
个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂。
在
中,
叫做底数,
叫做指数。
幂
读作
的
次方,也可以读作
的
次幂。
指数
因数的个数
底数
因数
相同因数
个相同的因数
相乘,即
我们把它记作
n个a相乘
幂的性质:
负数的奇次幂是负数,负数的
偶次幂是正数;
正数的任何次幂都是正数;
0
的任何正整数次幂是
0
。
细胞分裂示意图
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
课后思考
§1.5.1
乘方
这种求
个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂。
在
中,
叫做底数,
叫做指数。
幂
读作
的
次方,也可以读作
的
次幂。
指数
因数的个数
底数
因数
相同因数
个相同的因数
相乘,即
我们把它记作
n个a相乘
口答
1)在
中,9是
数,4是
数,读作
;表示
个
相乘的积。
2)
7的底数是
,指数是
,读
作
;表示
个
相乘的积。
7
的7次方
底
指
9的4次方(或9的4次幂)
4
9
7
3)在
中,-3是
数,16是
数,读作
;表示
个
相乘的积。
4)在
中,底数是
;指数是
;读作
;表示
个
相乘的积。
底
指
-3的16次方
17
的17次方
16
(-3)
17
5)51的底数是
,指数是
,可读作
;
6)
看成幂的话,底数是
,指数是
,可读作
;
幂
指数
底数
5
1
5的一次方
1
a的一次方
1
a
幂
指数
底数
a
课堂练习
一、把下列乘法式子写成乘方的形式:
1、1×1×1×1×1×1×1=
;
2、3×3×3×3×3=
;
3、(-3)×(-3)×(-3)×(-3)=
;
4、
=
;
二、把下列乘方写成乘法的形式:
1、
=
;
2、
=
;
3、
=
;
思考:用乘方式子怎么表示
的相反数?
-
答案:
课堂练习
判断下列各题是否正确:
(
)①
;
(
)②
;
(
)③
;
(
)④
对
错
错
错
解决下列问题,你能从中发现什么?
(1)
32与23有什么区别?各等于什么?
(2)
-34和(-3)
4有什么区别?各等于什么?
(3)2×32和(2×3)2
有什么区别?
(4)
有什么区别?各等于什么?
交流与思考
解决下列问题,你能从中发现什么?
(1)
32与23有什么区别?各等于什么?
(2)
-34和(-3)
4有什么区别?各等于什么?
答:(1)
32表示3的2次幂;而23表示2的3次幂,
它们的结果分别是9和8.
(2)-34表示4个3相乘的积的相反数或3的4次幂的相反数,结果是-81
;而(-3)
4则表示4个(-3)相乘的积或(-3)的4次幂,结果是81.
交流与思考
解决下列问题,你能从中发现什么?
(3)2×32和(2×3)2
有什么区别?
(4)
有什么区别?各等于什么?
答:
(3)
2×32表示
2与3的平方之积,等于18;
而(2×3)2表示2与3的积的平方,等于36.
交流与思考
例1计算:
解:
如果幂的底数是正数,那么这个幂有可能是负数吗?
不可能!正数的任何次幂是都是正数
从例1,你发现负数的幂的正负有什么规律?
当指数是
数时,负数的幂是
数;
当指数是
数时,负数的幂是
数。
幂的性质:
负数的奇次幂是负数,负数的
偶次幂是正数;
正数的任何次幂都是正数;
0
的任何正整数次幂是
0
。
口答
1)
是
(填“正”或“负”)数;
2)
是
(填“正”或“负”)数;
3)
=
;
4)
=
;
1
1
正
负
课堂练习
(课本第43-44页,练习第2题)
计算:
(1)
(-1)10
(2)(-1)7
(3)83
(4)
(-5)3
(5)(0.1)3
(6)(
)4
(7)(-10)4
(8)(-10)5
珠穆朗玛峰是世界的最高峰,它的海拔高度是8848米。
把一张足够大的厚度为0.1毫米的纸,连续对折30次的厚度能超过珠穆朗玛峰?
≈
≈
想一想
想一想
若对折30次,算式中有几个2相乘?
对折2次可裁成4张,即2×2=22张;
对折3次可裁成8张,即2×2×2=23张;
问题:
若对折10次可裁成几张?请用一个算式表示(不用算出结果)
动手做一做
解:
对折30次后的厚度为
折叠30次后的厚度超过珠穆朗玛峰
这种求
个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂。
在
中,
叫做底数,
叫做指数。
幂
读作
的
次方,也可以读作
的
次幂。
指数
因数的个数
底数
因数
相同因数
个相同的因数
相乘,即
我们把它记作
n个a相乘
幂的性质:
负数的奇次幂是负数,负数的
偶次幂是正数;
正数的任何次幂都是正数;
0
的任何正整数次幂是
0
。
细胞分裂示意图
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
课后思考
