【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.1第一课时
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.1第一课时 |

|
|
| 格式 | rar | ||
| 文件大小 | 373.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:33:54 | ||
图片预览



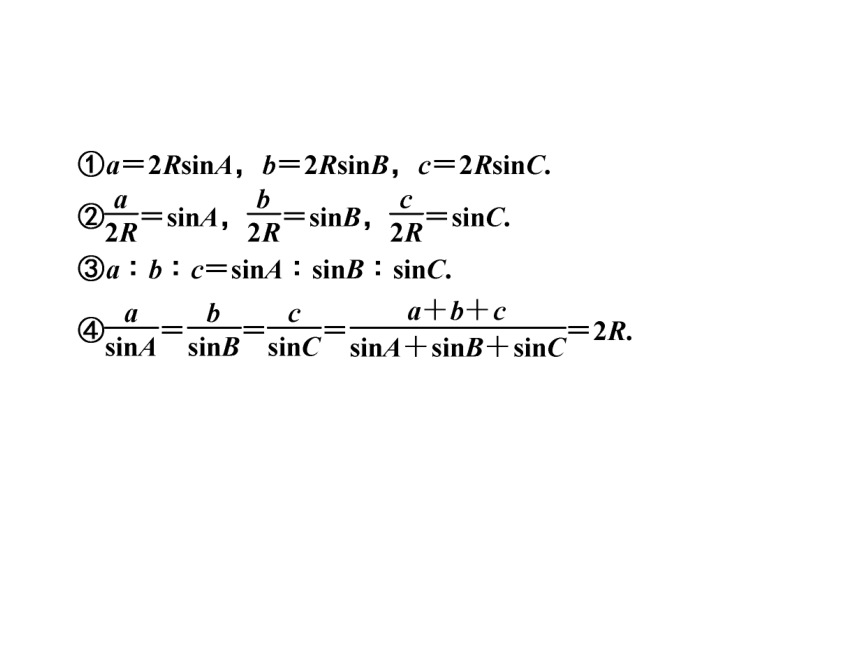





文档简介
(共25张PPT)
1.1 正弦定理
第一课时
课标要求:1.通过对三角形中边角关系的探索,掌握正弦定理的推导过程.
2.理解正弦定理及适用范围,会用正弦定理及其变式解决一些简单的解三角形问题.
重点难点:本节重点:对正弦定理的推理的理解及正弦定理的掌握.
本节难点:正弦定理的推理.
课标定位
基础知识梳理
1.正弦定理
在一个三角形中,各_____和它所对角的_____的_____相等,即__________________.
说明:(1)各边和它所对角的正弦之比为一个定值,这个定值为该三角形的外接圆直径;
(2)定理的变式(R为△ABC外接圆的半径):
边
正弦
比
2.解斜三角形
解斜三角形是指由六个元素(三条边和三个角)中的三个元素(至少有一个是边),求出其余三个未知元素的过程.
3.正弦定理在解三角形中的作用
(1)如果已知三角形的任意两个____与一____,由三角形________________,可以计算出三角形的另一____,并由正弦定理计算出三角形的另两____.
(2)如果已知三角形的任意_______与其中一边的_____,应用正弦定理,可以计算出另一边的对角,进而确定这个三角形其他的__________.
角
边
内角和为180°
角
边
两边
对角
边和角
课堂互动讲练
题型一
已知两角及一边解三角形
如果已知三角形的任意两个角与一边,由三角形内角和定理,可以计算出三角形的另一角,并由正弦定理计算出三角形的另两边.
已知在△ABC中,c=10,A=45°,C=30°,求a、b和B.
【分析】 已知两角及一边,先利用内角和为180°,求出B,再利用正弦定理求解.
例1
【点评】 在运算过程中,要用到三角函数中的公式,此题中对75°角作了“拆角”变换.
1.在△ABC中, a=5,B=45°,C=105°,求边c.
变式训练
已知三角形中两边和其中一边的对角解三角形问题,首先求出另一边的对角的正弦值,其次根据该正弦值求角时,需对角的情况讨论是否有解,如果有解,是一解还是两解.
题型二
已知两边和其中一边的对角解三角形
例2
【分析】 △ABC中已知两边和其中一边的对角,由正弦定理先求出另一边对角的正弦值,然后再求解其他边角.
【点评】 在△ABC中,已知两边a、b和边b的对角B,解三角形时可先用正弦定理求出角A的正弦值,确定角A时解不确定,应注意讨论,往往利用已知边a、b的大小关系,得到角A与B的大小关系,从而确定角A的解的个数.
互动探究
判断三角形的形状主要有两条途径:①化边为角;②化角为边.
题型三
利用正弦定理判断三角形的形状
在△ABC中,若acosA=bcosB,求证:△ABC是等腰三角形或直角三角形.
【分析】 观察已知条件,可以应用正弦定理把边化为角,再利用三角公式求解.
【证明】 由正弦定理的变式得a=2RsinA,b=2RsinB,
∵acosA=bcosB,
∴2RsinAcosA=2RsinBcosB,
∴sin2A=sin2B,
∴2A=2B或2A=π-2B,
例3
【点评】 利用正弦定理判断三角形的形状,关键是将已知条件中的边角关系转化为角或边的关系.本题应利用公式a=2RsinA,b=2RsinB,c=2RsinC将边角统一后,再利用两角和与差的正弦公式进行化简、判断,但由sin2A=sin2B,得角A和B的关系时容易漏掉2A=π-2B.
3.在△ABC中,已知a2tanB=b2tanA,试判断△ABC的形状.
变式训练
规律方法总结
常用的公式、结论
△ABC中角A、B、C的对边分别为a、b、c.
(1)A+B+C=180°;
(2)a<b A<B 2RsinA<2RsinB sinA<sinB;
(3)若角A为最小角,则0°<A<60°;若角A为最大角,则A>60°;
(4)勾股定理:
△ABC是以角C为直角的直角三角形 a2+b2=c2 sin2A+sin2B=sin2C C=90°.
△ABC是以角A为直角的直角三角形 b2+c2=a2 sin2B+sin2C=sin2A A=90°.
△ABC是以角B为直角的直角三角形 a2+c2=b2 sin2A+sin2C=sin2B B=90°.
随堂即时巩固
课时活页训练
1.1 正弦定理
第一课时
课标要求:1.通过对三角形中边角关系的探索,掌握正弦定理的推导过程.
2.理解正弦定理及适用范围,会用正弦定理及其变式解决一些简单的解三角形问题.
重点难点:本节重点:对正弦定理的推理的理解及正弦定理的掌握.
本节难点:正弦定理的推理.
课标定位
基础知识梳理
1.正弦定理
在一个三角形中,各_____和它所对角的_____的_____相等,即__________________.
说明:(1)各边和它所对角的正弦之比为一个定值,这个定值为该三角形的外接圆直径;
(2)定理的变式(R为△ABC外接圆的半径):
边
正弦
比
2.解斜三角形
解斜三角形是指由六个元素(三条边和三个角)中的三个元素(至少有一个是边),求出其余三个未知元素的过程.
3.正弦定理在解三角形中的作用
(1)如果已知三角形的任意两个____与一____,由三角形________________,可以计算出三角形的另一____,并由正弦定理计算出三角形的另两____.
(2)如果已知三角形的任意_______与其中一边的_____,应用正弦定理,可以计算出另一边的对角,进而确定这个三角形其他的__________.
角
边
内角和为180°
角
边
两边
对角
边和角
课堂互动讲练
题型一
已知两角及一边解三角形
如果已知三角形的任意两个角与一边,由三角形内角和定理,可以计算出三角形的另一角,并由正弦定理计算出三角形的另两边.
已知在△ABC中,c=10,A=45°,C=30°,求a、b和B.
【分析】 已知两角及一边,先利用内角和为180°,求出B,再利用正弦定理求解.
例1
【点评】 在运算过程中,要用到三角函数中的公式,此题中对75°角作了“拆角”变换.
1.在△ABC中, a=5,B=45°,C=105°,求边c.
变式训练
已知三角形中两边和其中一边的对角解三角形问题,首先求出另一边的对角的正弦值,其次根据该正弦值求角时,需对角的情况讨论是否有解,如果有解,是一解还是两解.
题型二
已知两边和其中一边的对角解三角形
例2
【分析】 △ABC中已知两边和其中一边的对角,由正弦定理先求出另一边对角的正弦值,然后再求解其他边角.
【点评】 在△ABC中,已知两边a、b和边b的对角B,解三角形时可先用正弦定理求出角A的正弦值,确定角A时解不确定,应注意讨论,往往利用已知边a、b的大小关系,得到角A与B的大小关系,从而确定角A的解的个数.
互动探究
判断三角形的形状主要有两条途径:①化边为角;②化角为边.
题型三
利用正弦定理判断三角形的形状
在△ABC中,若acosA=bcosB,求证:△ABC是等腰三角形或直角三角形.
【分析】 观察已知条件,可以应用正弦定理把边化为角,再利用三角公式求解.
【证明】 由正弦定理的变式得a=2RsinA,b=2RsinB,
∵acosA=bcosB,
∴2RsinAcosA=2RsinBcosB,
∴sin2A=sin2B,
∴2A=2B或2A=π-2B,
例3
【点评】 利用正弦定理判断三角形的形状,关键是将已知条件中的边角关系转化为角或边的关系.本题应利用公式a=2RsinA,b=2RsinB,c=2RsinC将边角统一后,再利用两角和与差的正弦公式进行化简、判断,但由sin2A=sin2B,得角A和B的关系时容易漏掉2A=π-2B.
3.在△ABC中,已知a2tanB=b2tanA,试判断△ABC的形状.
变式训练
规律方法总结
常用的公式、结论
△ABC中角A、B、C的对边分别为a、b、c.
(1)A+B+C=180°;
(2)a<b A<B 2RsinA<2RsinB sinA<sinB;
(3)若角A为最小角,则0°<A<60°;若角A为最大角,则A>60°;
(4)勾股定理:
△ABC是以角C为直角的直角三角形 a2+b2=c2 sin2A+sin2B=sin2C C=90°.
△ABC是以角A为直角的直角三角形 b2+c2=a2 sin2B+sin2C=sin2A A=90°.
△ABC是以角B为直角的直角三角形 a2+c2=b2 sin2A+sin2C=sin2B B=90°.
随堂即时巩固
课时活页训练
