【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.2第一课时
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.2第一课时 |  | |
| 格式 | rar | ||
| 文件大小 | 520.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:33:54 | ||
图片预览



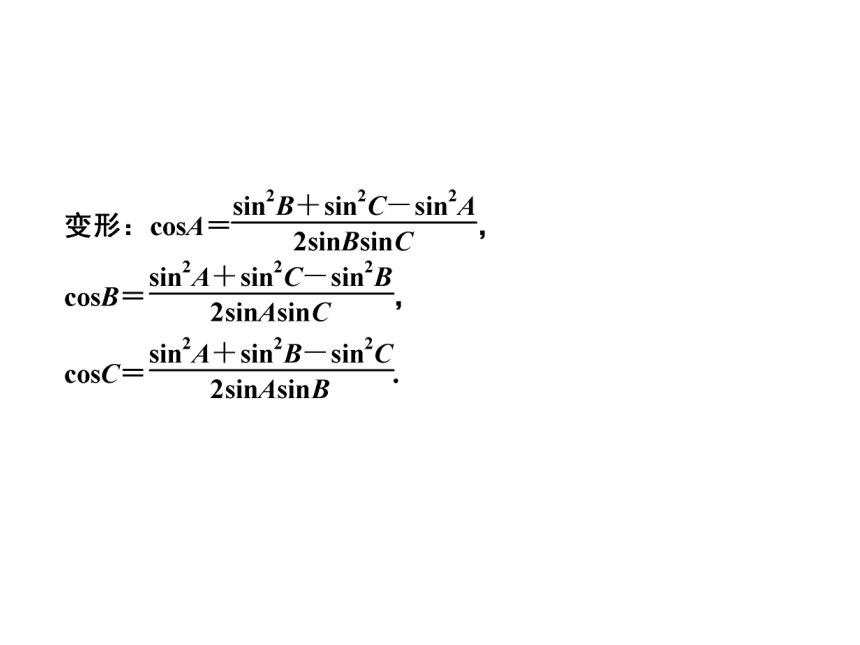



文档简介
(共29张PPT)
1.2 余弦定理
第一课时
课标要求:1.理解并掌握余弦定理.
2.掌握用向量的数量积证明余弦定理的方法.
3.余弦定理的简单应用.
重点难点:本节重点:余弦定理及其应用.
本节难点:用向量的数量积证明余弦定理.
课标定位
基础知识梳理
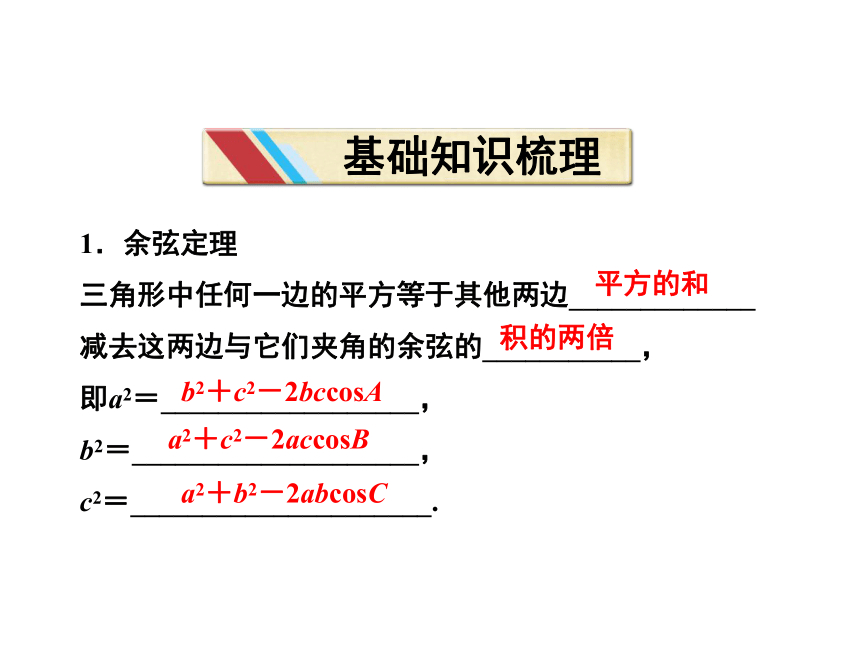
1.余弦定理
三角形中任何一边的平方等于其他两边_____________减去这两边与它们夹角的余弦的___________,
即a2=__________________,
b2=____________________,
c2=_____________________.
平方的和
积的两倍
b2+c2-2bccosA
a2+c2-2accosB
a2+b2-2abcosC
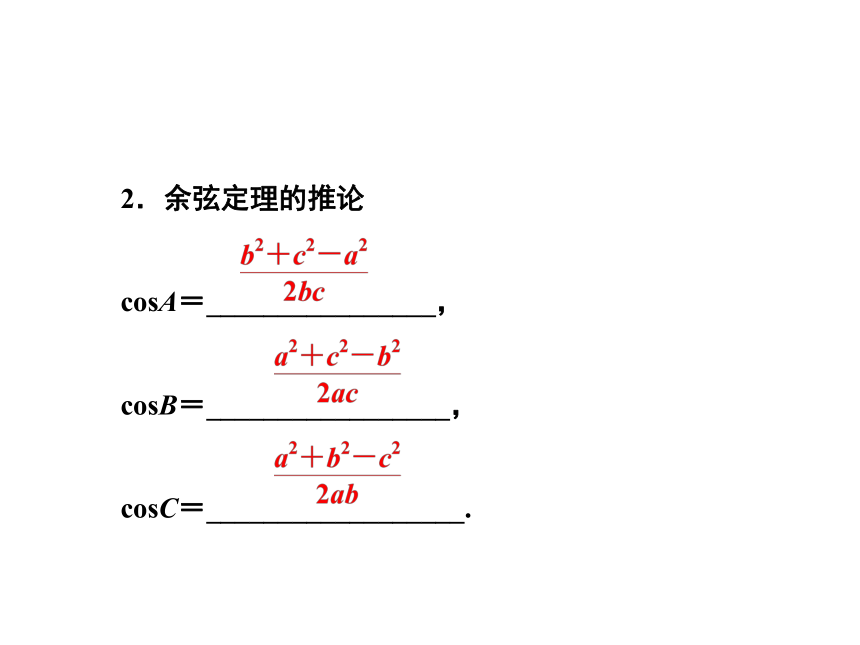
2.余弦定理的推论
cosA=________________,
cosB=_________________,
cosC=__________________.
说明:(1)将余弦定理中的a,b,c,分别换成2RsinA,2RsinB,2RsinC,
可得:sin2A=sin2B+sin2C-2sinBsinCcosA,
sin2B=sin2A+sin2C-2sinAsinCcosB,
sin2C=sin2A+sin2B-2sinAsinBcosC.
(2)余弦定理是勾股定理的推广,勾股定理是余弦定理的特殊情况.
3.运用余弦定理可以解决两类解三角形问题
(1)已知______________,求第三边和____________;
(2)已知三边,求_______________.
两边及其夹角
其他两个角
三个角
课堂互动讲练
题型一
已知三角形的两边及其夹角解三角形
这类题目的基本解法是先用余弦定理求第三边,再用正弦定理或余弦定理求另一角,最后用三角形内角和定理求第三个角.
例1
【分析】 注意根与系数的关系的运用及公式cosC=cos[π-(A+B)]=-cos(A+B).
变式训练
题型二
已知三角形三边解三角形
这类问题的基本解法是先用余弦定理求出两个角,再用三角形内角和定理求出第三个角.
例2
【分析】 由比例的性质可以引入一个字母k,用k表示a、b、c,再由余弦定理求解各角.
变式训练
题型三
已知三角形的两边和其中一边的对角,解三角形
解决此类问题有两种方法,比较下列两种解法,从中体会各自的优点.
例3
【分析】 解答本题可先由正弦定理求出角A,然后再求边c;也可由余弦定理列出关于边长c的方程.
变式训练
规律方法总结
解三角形可以分成以下四种类型:(1)已知三边,求三角(可以利用余弦定理的推论).(2)已知两边及夹角,求另两角和另一边(可以先用余弦定理求第三边,再用正弦定理或余弦定理求其余两角).(3)已知两边及其中一边的对角,求另一边和其余两角(可以先用正弦定理求出另一角,再求其余边角,或者先用余弦定理求出第三边,再求其余两角).(4)已知两角及一边,求另一角和其余两边(先由三角形内角和为180°,求出另一角,再用正弦定理或余弦定理求出其余两边).
由以上四种情况可知,要解一个三角形至少需要一边.
随堂即时巩固
课时活页训练
即时突破
例1
题型一
导数定义的应用
1.2 余弦定理
第一课时
课标要求:1.理解并掌握余弦定理.
2.掌握用向量的数量积证明余弦定理的方法.
3.余弦定理的简单应用.
重点难点:本节重点:余弦定理及其应用.
本节难点:用向量的数量积证明余弦定理.
课标定位
基础知识梳理
1.余弦定理
三角形中任何一边的平方等于其他两边_____________减去这两边与它们夹角的余弦的___________,
即a2=__________________,
b2=____________________,
c2=_____________________.
平方的和
积的两倍
b2+c2-2bccosA
a2+c2-2accosB
a2+b2-2abcosC
2.余弦定理的推论
cosA=________________,
cosB=_________________,
cosC=__________________.
说明:(1)将余弦定理中的a,b,c,分别换成2RsinA,2RsinB,2RsinC,
可得:sin2A=sin2B+sin2C-2sinBsinCcosA,
sin2B=sin2A+sin2C-2sinAsinCcosB,
sin2C=sin2A+sin2B-2sinAsinBcosC.
(2)余弦定理是勾股定理的推广,勾股定理是余弦定理的特殊情况.
3.运用余弦定理可以解决两类解三角形问题
(1)已知______________,求第三边和____________;
(2)已知三边,求_______________.
两边及其夹角
其他两个角
三个角
课堂互动讲练
题型一
已知三角形的两边及其夹角解三角形
这类题目的基本解法是先用余弦定理求第三边,再用正弦定理或余弦定理求另一角,最后用三角形内角和定理求第三个角.
例1
【分析】 注意根与系数的关系的运用及公式cosC=cos[π-(A+B)]=-cos(A+B).
变式训练
题型二
已知三角形三边解三角形
这类问题的基本解法是先用余弦定理求出两个角,再用三角形内角和定理求出第三个角.
例2
【分析】 由比例的性质可以引入一个字母k,用k表示a、b、c,再由余弦定理求解各角.
变式训练
题型三
已知三角形的两边和其中一边的对角,解三角形
解决此类问题有两种方法,比较下列两种解法,从中体会各自的优点.
例3
【分析】 解答本题可先由正弦定理求出角A,然后再求边c;也可由余弦定理列出关于边长c的方程.
变式训练
规律方法总结
解三角形可以分成以下四种类型:(1)已知三边,求三角(可以利用余弦定理的推论).(2)已知两边及夹角,求另两角和另一边(可以先用余弦定理求第三边,再用正弦定理或余弦定理求其余两角).(3)已知两边及其中一边的对角,求另一边和其余两角(可以先用正弦定理求出另一角,再求其余边角,或者先用余弦定理求出第三边,再求其余两角).(4)已知两角及一边,求另一角和其余两边(先由三角形内角和为180°,求出另一角,再用正弦定理或余弦定理求出其余两边).
由以上四种情况可知,要解一个三角形至少需要一边.
随堂即时巩固
课时活页训练
即时突破
例1
题型一
导数定义的应用
