【2012优化方案 精品课件】苏教版 数学 必修5:第二章2.3.3节第一课时
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第二章2.3.3节第一课时 |

|
|
| 格式 | rar | ||
| 文件大小 | 484.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:33:54 | ||
图片预览








文档简介
(共23张PPT)
2.3.3 等比数列的前n项和
第一课时
课标要求:1.掌握等比数列前n项和公式及推导方法(错位相减法).
2.会运用等比数列前n项和公式进行基本量的计算,并能进行简单应用.
重点难点:本节重点:推导并掌握等比数列的前n项和公式;
本节难点:错位相减法的应用.
课标定位
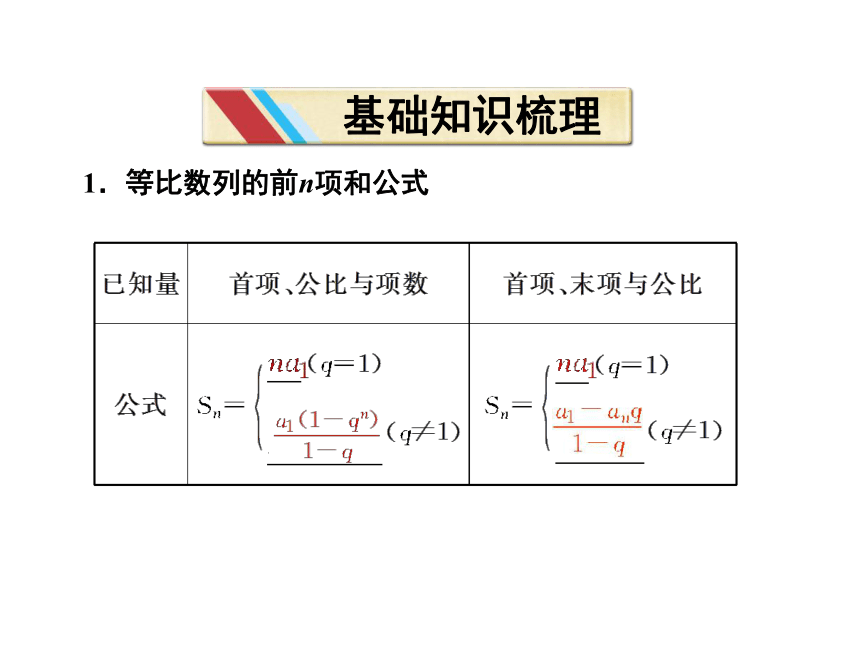
基础知识梳理
1.等比数列的前n项和公式
课堂互动讲练
题型一
等比数列前n项和公式的基本运算
求数列前n项和,应抓住其核心——通项.
例1
设等比数列{an}的公比q<1,前n项和为Sn,已知a3=2,S4=5S2,求{an}的通项公式.
【分析】 解答本题应当建立a1与q的方程组求解.
【点评】 运用等比数列的前n项和公式要注意公比q=1和q≠1两种情形,在解有关的方程组时,通常用约分或两式相除的方法进行消元.
变式训练
错位相减法适合求一个等差数列与一个等比数列相应项相乘得到的新数列的前n项和,即已知{an}为等差数列,{bn}为等比数列,利用错位相减法可求数列{anbn}的前n项和,因而具有一般性,其它方法求和可使学生进一步认识q≠1时,等比数列前n项和的特征,也能进一步开拓求和思路.
题型二
“错位相减法”及其应用
例2
【点评】 要注意本题特点.它是形如{anbn}数列的前n项的和.其中{an}是等差数列,{bn}是等比数列.具体解法是:乘等比数列的公比或倒数然后错位相减,使其转化为等比数列问题来解.
变式训练
求和:Sn=1+3x+5x2+7x3+…+(2n-1)·xn-1(x≠0).
【分析】 由题可知通项{(2n-1)xn-1}是等差数列{2n-1}的通项与等比数列{xn-1} 的通项之积.
例3
【点评】 这种方法是在推导等比数列的前n项和公式时所用的方法,即错位相减法求和.
规律方法总结
1.等比数列的前n项和给出了数列求和的一种常用的方法——错位相减法,这种方法对解决数列{anbn}的前n项和(其中{an}成等差数列,{bn}成等比数列)是相当有效的.
2.应用求和公式时q≠1,必要时应讨论q=1的情况.即:当q=1时,Sn=na1;当q≠1时,前n项和必须具备形式Sn=A(qn-1)(A≠0).
随堂即时巩固
课时活页训练
2.3.3 等比数列的前n项和
第一课时
课标要求:1.掌握等比数列前n项和公式及推导方法(错位相减法).
2.会运用等比数列前n项和公式进行基本量的计算,并能进行简单应用.
重点难点:本节重点:推导并掌握等比数列的前n项和公式;
本节难点:错位相减法的应用.
课标定位
基础知识梳理
1.等比数列的前n项和公式
课堂互动讲练
题型一
等比数列前n项和公式的基本运算
求数列前n项和,应抓住其核心——通项.
例1
设等比数列{an}的公比q<1,前n项和为Sn,已知a3=2,S4=5S2,求{an}的通项公式.
【分析】 解答本题应当建立a1与q的方程组求解.
【点评】 运用等比数列的前n项和公式要注意公比q=1和q≠1两种情形,在解有关的方程组时,通常用约分或两式相除的方法进行消元.
变式训练
错位相减法适合求一个等差数列与一个等比数列相应项相乘得到的新数列的前n项和,即已知{an}为等差数列,{bn}为等比数列,利用错位相减法可求数列{anbn}的前n项和,因而具有一般性,其它方法求和可使学生进一步认识q≠1时,等比数列前n项和的特征,也能进一步开拓求和思路.
题型二
“错位相减法”及其应用
例2
【点评】 要注意本题特点.它是形如{anbn}数列的前n项的和.其中{an}是等差数列,{bn}是等比数列.具体解法是:乘等比数列的公比或倒数然后错位相减,使其转化为等比数列问题来解.
变式训练
求和:Sn=1+3x+5x2+7x3+…+(2n-1)·xn-1(x≠0).
【分析】 由题可知通项{(2n-1)xn-1}是等差数列{2n-1}的通项与等比数列{xn-1} 的通项之积.
例3
【点评】 这种方法是在推导等比数列的前n项和公式时所用的方法,即错位相减法求和.
规律方法总结
1.等比数列的前n项和给出了数列求和的一种常用的方法——错位相减法,这种方法对解决数列{anbn}的前n项和(其中{an}成等差数列,{bn}成等比数列)是相当有效的.
2.应用求和公式时q≠1,必要时应讨论q=1的情况.即:当q=1时,Sn=na1;当q≠1时,前n项和必须具备形式Sn=A(qn-1)(A≠0).
随堂即时巩固
课时活页训练
