【2012优化方案 精品课件】苏教版 数学 必修5:第三章3.1节
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第三章3.1节 |

|
|
| 格式 | rar | ||
| 文件大小 | 542.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:33:54 | ||
图片预览








文档简介
(共28张PPT)
第三章 不等式
3.1 不等关系
课标要求:1.通过实际问题感受现实世界中的相等关系和不等关系,理解不等关系是普遍存在的.
2.会用不等式(组)表示一些简单的不等关系,掌握不等式的常用性质.
重点难点:本节重点:用不等式(组)表示实际问题中的不等关系,并用不等式(组)研究含有不等关系的问题.
本节难点:通过具体情境建立不等式模型.
课标定位
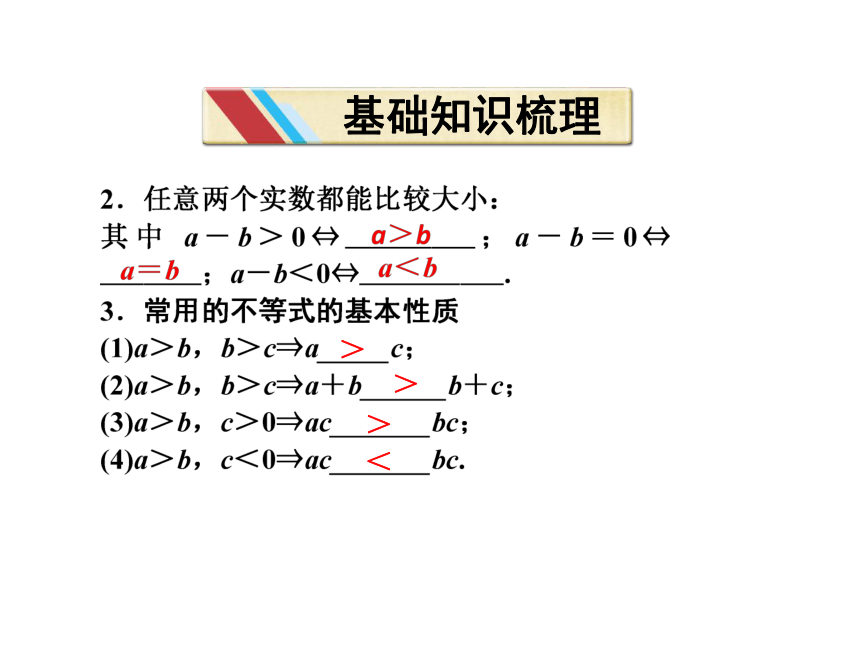
基础知识梳理
>
<
>
>
课堂互动讲练
题型一
用不等式(组)表示不等关系
用不等式(组)表示实际问题中的不等关系时,首先应读懂题意,设出未知量,寻找不等关系的根源,将不等关系用未知量表示出来,即得到不等式或不等式组,这是应用不等式(组)解决实际问题的最基本的一步.
例1
某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘,根据需要,软件至少买3片,磁盘至少买两盒,写出满足上述所有不等关系的不等式(组).
【分析】 假设购买单片软件和盒装磁盘分别为x片、y盒,根据题意,应有下列不等关系:
(1)总费用不超过500元;
(2)软件至少买3片;
(3)磁盘至少买两盒.
用关于x、y的不等式(组)表示上述不等关系即可.
【点评】 将实际问题通过数学建模,用不等式(组)刻画不等关系首先要设出未知数,把文字语言用不等式语言表示即可.
变式训练
比较大小问题,通常用作差法来解决,步骤可归纳为:作差、变形、判定符号、得出结论.如需分类讨论,分类讨论后要作出总结结论.
已知x<1,比较x3-1与2x2-2x的大小.
【分析】 解答本题可先作差,然后再因式分解进行变形.
题型二
比较大小问题
例2
【点评】 作差法比较两个数的大小,变形是关键,一般变形越彻底越有利于下一步的判断,常用知识有因式分解,配方,通分,对数的运算性质等,另外还要注意分类讨论.
变式训练
题型三
实际应用题
注意实际应用题数学模型的建立方法,求解出数据后,要善于用这些数据对问题作出合理的解释.
某单位组织职工去某地参观学习需包车前往.甲车队说:“如领队买全票一张,其余人可享受7.5折优惠”,乙车队说:“你们属团体票,按原价的8折优惠”.这两车队的原价、车型都是一样的,试根据单位去的人数,比较两车队的收费哪家更优惠.
例3
【分析】 由题目可获取以下主要信息:
①单位职工人数未知,是变量;
②全票价未知,是常量.
解答本题可先正确建立函数模型,再运用作差法加以比较即可.
【点评】 解决决策优化型应用题,首先要确定制约着决策优化的关键量是哪一个,然后再用作差法比较它们的大小即可.
3.一群女生住若干间宿舍,若每间住4人,剩19人无房住;若每间住6人,有一间宿舍住不满,问可能有多少间宿舍?多少名学生?
变式训练
题型四
不等式的性质及应用
例4
使用不等式性质时,一定要注意不等式成立的条件,不要弱化条件,尤其是不能凭想当然随意捏造性质.
【分析】 解答本题可利用不等式的可加性和可乘性求解.
变式训练
规律方法总结
1.不等式的性质是证明不等式与解不等式的重要而又基本的依据,必须要正确、熟练地掌握,要弄清每一性质的条件和结论.注意条件的放宽和加强,条件和结论之间的相互联系.
2.使用“作差”比较,其变形之一是将差式因式分解,然后根据各个因式的符号判断差式的符号;变形之二是将差式变成非负数(或非正数)之和,然后判断差式的符号.
3.关于数(式)比较大小,应该将“相等”与“不等”分开加以说明,不要笼统地写成“A≥B(或B≤A)”.
随堂即时巩固
课时活页训练
第三章 不等式
3.1 不等关系
课标要求:1.通过实际问题感受现实世界中的相等关系和不等关系,理解不等关系是普遍存在的.
2.会用不等式(组)表示一些简单的不等关系,掌握不等式的常用性质.
重点难点:本节重点:用不等式(组)表示实际问题中的不等关系,并用不等式(组)研究含有不等关系的问题.
本节难点:通过具体情境建立不等式模型.
课标定位
基础知识梳理
>
<
>
>
课堂互动讲练
题型一
用不等式(组)表示不等关系
用不等式(组)表示实际问题中的不等关系时,首先应读懂题意,设出未知量,寻找不等关系的根源,将不等关系用未知量表示出来,即得到不等式或不等式组,这是应用不等式(组)解决实际问题的最基本的一步.
例1
某电脑用户计划使用不超过500元的资金购买单价分别为60元、70元的单片软件和盒装磁盘,根据需要,软件至少买3片,磁盘至少买两盒,写出满足上述所有不等关系的不等式(组).
【分析】 假设购买单片软件和盒装磁盘分别为x片、y盒,根据题意,应有下列不等关系:
(1)总费用不超过500元;
(2)软件至少买3片;
(3)磁盘至少买两盒.
用关于x、y的不等式(组)表示上述不等关系即可.
【点评】 将实际问题通过数学建模,用不等式(组)刻画不等关系首先要设出未知数,把文字语言用不等式语言表示即可.
变式训练
比较大小问题,通常用作差法来解决,步骤可归纳为:作差、变形、判定符号、得出结论.如需分类讨论,分类讨论后要作出总结结论.
已知x<1,比较x3-1与2x2-2x的大小.
【分析】 解答本题可先作差,然后再因式分解进行变形.
题型二
比较大小问题
例2
【点评】 作差法比较两个数的大小,变形是关键,一般变形越彻底越有利于下一步的判断,常用知识有因式分解,配方,通分,对数的运算性质等,另外还要注意分类讨论.
变式训练
题型三
实际应用题
注意实际应用题数学模型的建立方法,求解出数据后,要善于用这些数据对问题作出合理的解释.
某单位组织职工去某地参观学习需包车前往.甲车队说:“如领队买全票一张,其余人可享受7.5折优惠”,乙车队说:“你们属团体票,按原价的8折优惠”.这两车队的原价、车型都是一样的,试根据单位去的人数,比较两车队的收费哪家更优惠.
例3
【分析】 由题目可获取以下主要信息:
①单位职工人数未知,是变量;
②全票价未知,是常量.
解答本题可先正确建立函数模型,再运用作差法加以比较即可.
【点评】 解决决策优化型应用题,首先要确定制约着决策优化的关键量是哪一个,然后再用作差法比较它们的大小即可.
3.一群女生住若干间宿舍,若每间住4人,剩19人无房住;若每间住6人,有一间宿舍住不满,问可能有多少间宿舍?多少名学生?
变式训练
题型四
不等式的性质及应用
例4
使用不等式性质时,一定要注意不等式成立的条件,不要弱化条件,尤其是不能凭想当然随意捏造性质.
【分析】 解答本题可利用不等式的可加性和可乘性求解.
变式训练
规律方法总结
1.不等式的性质是证明不等式与解不等式的重要而又基本的依据,必须要正确、熟练地掌握,要弄清每一性质的条件和结论.注意条件的放宽和加强,条件和结论之间的相互联系.
2.使用“作差”比较,其变形之一是将差式因式分解,然后根据各个因式的符号判断差式的符号;变形之二是将差式变成非负数(或非正数)之和,然后判断差式的符号.
3.关于数(式)比较大小,应该将“相等”与“不等”分开加以说明,不要笼统地写成“A≥B(或B≤A)”.
随堂即时巩固
课时活页训练
