【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.1第二课时
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.1第二课时 |

|
|
| 格式 | rar | ||
| 文件大小 | 517.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 00:00:00 | ||
图片预览







文档简介
(共29张PPT)
第二课时
课标要求:1.掌握正弦定理及其变式的结构特征和功能,明确应用正弦定理解斜三角形的可解类型,能熟练地运用正弦定理解斜三角形,会用计算器求三角形的近似解.
2.探究三角形面积公式的表现形式,会结合正弦定理解与面积有关的斜三角形问题.
重点难点:本节重点:三角形面积公式的理解及应用.
本节难点:三角形解的个数的判定.
课标定位
基础知识梳理
1.三角形面积公式
(1)S△=________=____________=__________.
(2)S△=________=_________=___________(其中ha,hb,hc分别表示三边a,b,c上的高)
2.已知两边a,b和一边的对角B,求角A时的解的情况
已知a、b和B,用正弦定理求A时,由于已知三角形的两边和其中一条边所对的角不能确定惟一的三角形,因此,解答此类题目时常常出现无解、一解、两解三种情况,具体解的情况如下:
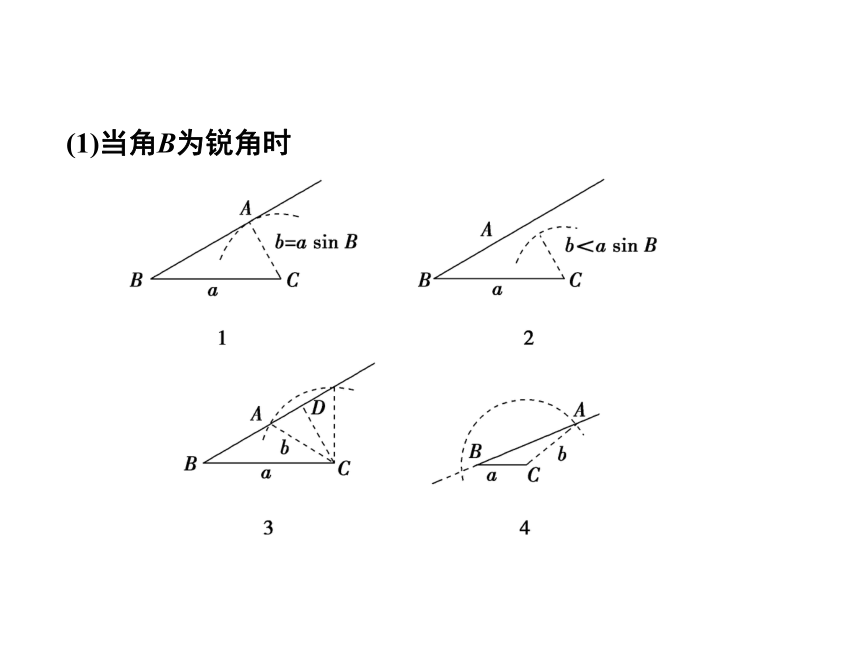
(1)当角B为锐角时
①当b=asinB时,如图1,以点C为圆心,以b为半径画弧,弧与射线BA相切,只有一个交点,此时三角形只有一解;
②当b<asinB时,如图2,以点C为圆心,以b为半径画弧,弧与射线BA相离,无交点,此时三角形无解;
③当asinB<b<a时,如图3,以点C为圆心,以b为半径画弧,弧与射线BA有两个交点,此时三角形有两解;
④当b>a时,如图4,以点C为圆心,以b为半径画弧,弧与射线BA只有一个交点,此时三角形只有一解;
⑤当b=a时,显然只有一解.
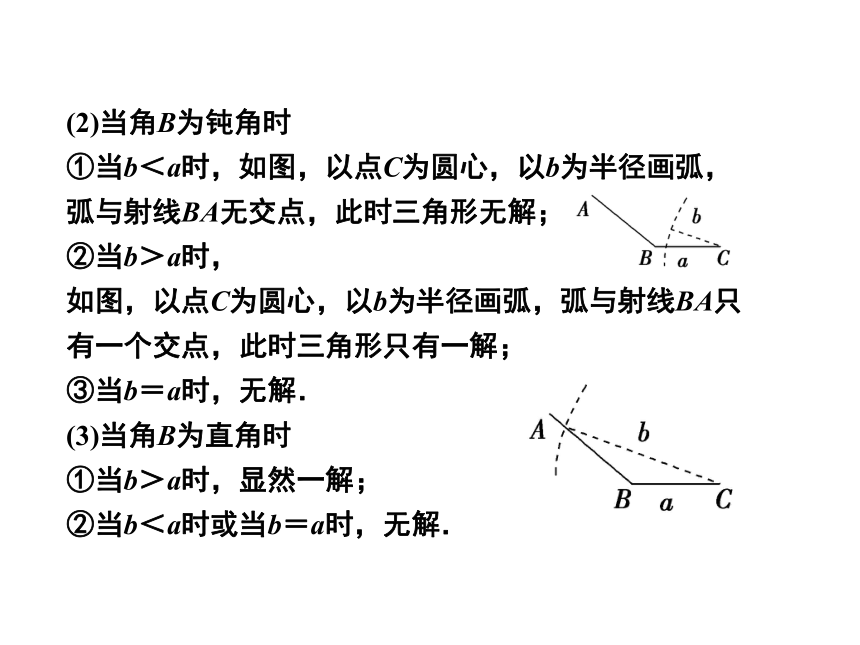
(2)当角B为钝角时
①当b<a时,如图,以点C为圆心,以b为半径画弧,弧与射线BA无交点,此时三角形无解;
②当b>a时,
如图,以点C为圆心,以b为半径画弧,弧与射线BA只有一个交点,此时三角形只有一解;
③当b=a时,无解.
(3)当角B为直角时
①当b>a时,显然一解;
②当b<a时或当b=a时,无解.
课堂互动讲练
题型一
三角形解的情况的判定
已知两边和其中一边的对角,求另一边的对角,从而进一步求出其它的边与角.由于三角形的形状不能惟一确定,因而会出现一解、两解和无解三种情况.可结合示意图进行判断.
例1
【分析】 画出示意图,由草图判定解的个数.
若sinA≤sinB,无解.
②a=b时,一解.
③a若sinA≥sinB,无解.
若sinA变式训练
题型二
利用三角形面积公式解决问题
例2
【点评】 本题主要考查三角形的边角关系和面积计算,灵活运用三角变换公式是解决问题的关键.
变式训练
题型三
正弦定理及其变形的简单应用
例3
【分析】 由结构a∶b∶c=1∶3∶5想到正弦定理的变式.
【点评】 利用比例性质可使问题简化.
规律方法总结
1.正弦定理表达了三角形的边和角的关系,其作用是解三角形,而且正弦定理有若干变形形式,应用正弦定理可以实现三角形中的边角关系的互相转换.通过应用还应发现它与三角函数、平面向量知识在解三角形中有密切的联系.
2.应用正弦定理,要明确角化边或边化角的方向,正确判断解的个数,特别注意对已知两边及一边对角时三角形解的个数的讨论,防止出现漏解或增解.
3.涉及求三角形中的边、面积等最值时,应注意使用正弦定理、面积公式等建立函数关系式,通过求三角函数的最值来解决问题.
4.在解三角形中,以下公式应记熟,记准,并能灵活运用:
A+B+C=π,sin(A+B)=sinC,cos(A+B)=-cosC,tan(A+B)=-tanC.
随堂即时巩固
课时活页训练
即时突破
例1
题型一
导数定义的应用
第二课时
课标要求:1.掌握正弦定理及其变式的结构特征和功能,明确应用正弦定理解斜三角形的可解类型,能熟练地运用正弦定理解斜三角形,会用计算器求三角形的近似解.
2.探究三角形面积公式的表现形式,会结合正弦定理解与面积有关的斜三角形问题.
重点难点:本节重点:三角形面积公式的理解及应用.
本节难点:三角形解的个数的判定.
课标定位
基础知识梳理
1.三角形面积公式
(1)S△=________=____________=__________.
(2)S△=________=_________=___________(其中ha,hb,hc分别表示三边a,b,c上的高)
2.已知两边a,b和一边的对角B,求角A时的解的情况
已知a、b和B,用正弦定理求A时,由于已知三角形的两边和其中一条边所对的角不能确定惟一的三角形,因此,解答此类题目时常常出现无解、一解、两解三种情况,具体解的情况如下:
(1)当角B为锐角时
①当b=asinB时,如图1,以点C为圆心,以b为半径画弧,弧与射线BA相切,只有一个交点,此时三角形只有一解;
②当b<asinB时,如图2,以点C为圆心,以b为半径画弧,弧与射线BA相离,无交点,此时三角形无解;
③当asinB<b<a时,如图3,以点C为圆心,以b为半径画弧,弧与射线BA有两个交点,此时三角形有两解;
④当b>a时,如图4,以点C为圆心,以b为半径画弧,弧与射线BA只有一个交点,此时三角形只有一解;
⑤当b=a时,显然只有一解.
(2)当角B为钝角时
①当b<a时,如图,以点C为圆心,以b为半径画弧,弧与射线BA无交点,此时三角形无解;
②当b>a时,
如图,以点C为圆心,以b为半径画弧,弧与射线BA只有一个交点,此时三角形只有一解;
③当b=a时,无解.
(3)当角B为直角时
①当b>a时,显然一解;
②当b<a时或当b=a时,无解.
课堂互动讲练
题型一
三角形解的情况的判定
已知两边和其中一边的对角,求另一边的对角,从而进一步求出其它的边与角.由于三角形的形状不能惟一确定,因而会出现一解、两解和无解三种情况.可结合示意图进行判断.
例1
【分析】 画出示意图,由草图判定解的个数.
若sinA≤sinB,无解.
②a=b时,一解.
③a
若sinA
题型二
利用三角形面积公式解决问题
例2
【点评】 本题主要考查三角形的边角关系和面积计算,灵活运用三角变换公式是解决问题的关键.
变式训练
题型三
正弦定理及其变形的简单应用
例3
【分析】 由结构a∶b∶c=1∶3∶5想到正弦定理的变式.
【点评】 利用比例性质可使问题简化.
规律方法总结
1.正弦定理表达了三角形的边和角的关系,其作用是解三角形,而且正弦定理有若干变形形式,应用正弦定理可以实现三角形中的边角关系的互相转换.通过应用还应发现它与三角函数、平面向量知识在解三角形中有密切的联系.
2.应用正弦定理,要明确角化边或边化角的方向,正确判断解的个数,特别注意对已知两边及一边对角时三角形解的个数的讨论,防止出现漏解或增解.
3.涉及求三角形中的边、面积等最值时,应注意使用正弦定理、面积公式等建立函数关系式,通过求三角函数的最值来解决问题.
4.在解三角形中,以下公式应记熟,记准,并能灵活运用:
A+B+C=π,sin(A+B)=sinC,cos(A+B)=-cosC,tan(A+B)=-tanC.
随堂即时巩固
课时活页训练
即时突破
例1
题型一
导数定义的应用
