【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.3第二课时
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.3第二课时 |  | |
| 格式 | rar | ||
| 文件大小 | 519.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:34:29 | ||
图片预览







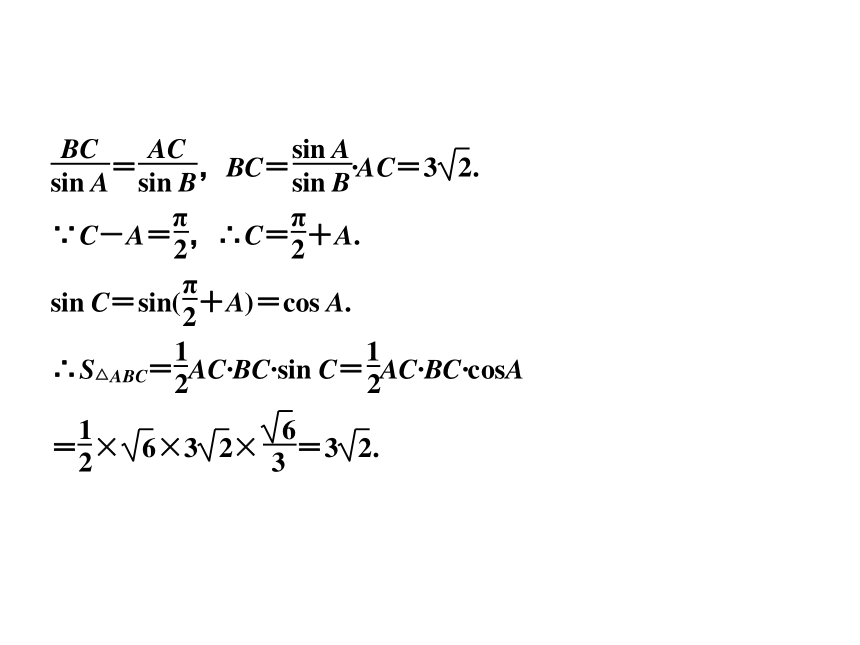
文档简介
(共29张PPT)
第二课时
课标要求:1.理解并掌握正弦定理、余弦定理、面积公式.
2.能正确运用正弦定理、余弦定理及关系式A+B+C=π解决三角形中的计算和证明问题.
重点难点:本节重点:熟练应用正、余弦定理解决三角形中的相关问题.
本节难点:三角形中的边角关系的建立.
课标定位
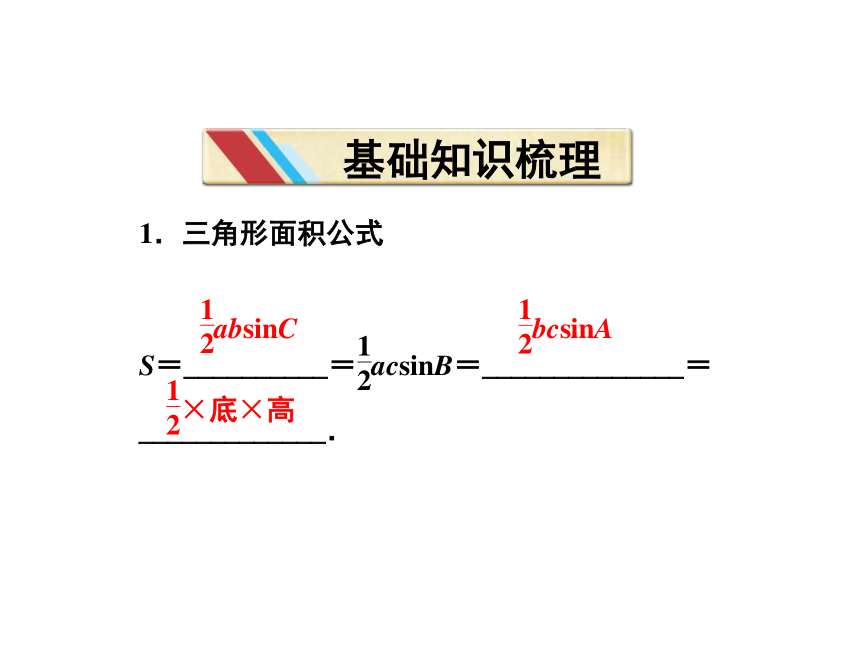
基础知识梳理
2.三角形内角和定理:_________________________.
说明:(1)正弦定理和余弦定理的主要作用:
①解三角形;
②判断三角形的形状;
③证明三角形中的恒等式.
(2)正弦定理和余弦定理的主要功能是实现三角形中边角关系的转化.
三角形的内角和是180°
课堂互动讲练
题型一
三角形的面积问题
在不同的已知条件下,求三角形面积的问题与解三角形有密切的关系,通常我们要根据已知条件,利用正弦定理、余弦定理求出需要的元素,从而求出三角形的面积.
例1
变式训练
求解最值问题,一般要把要求最值的量用一个变量表示出来,并且要确定变量的取值范围,对于三角形中的最值问题,要充分利用正、余弦定理及面积公式,运用三角函数的性质求最值.
题型二
三角形中的最值问题
已知△ABC内接于半径为R的圆中,且满足关系式2R(sin2A-sin2C)=(a-b)sinB,求△ABC面积的最大值.
【分析】 求面积的最值,应先根据条件写出面积的表达式,再根据表达式求最值.
例2
【点评】 本题综合运用正、余弦定理,把边化成角,再利用三角函数的有界性解决.
2.在△ABC中,a+b=10,且cosC是方程2x2-3x-2=0的一个根,求△ABC周长的最小值.
变式训练
在几何中有关三角函数计算、证明,平面图形的边长、面积等求解经常用到正、余弦定理.
题型三
正、余弦定理在几何计算中的应用
例3
【分析】 由条件知可以由余弦定理求出cosA的值,而要求的式子中含有sinA、tanA,故只要由sin2A+cos2A=1求出sinA即可.
【点评】 本题将余弦定理与三角求值结合在一起,解题的关键是求出cosA.
变式训练
答案:30°
规律方法总结
在解三角形问题时,一定要根据具体情况,恰当地选用正弦定理或余弦定理,公式选择得当、方法运用巧妙是简化问题的必要手段,同时还要注意与三角形的其他知识的综合运用.如:三角形内角和定理,大边对大角,两边之和大于第三边,两边之差小于第三边,三角形的面积公式等.
随堂即时巩固
课时活页训练
第二课时
课标要求:1.理解并掌握正弦定理、余弦定理、面积公式.
2.能正确运用正弦定理、余弦定理及关系式A+B+C=π解决三角形中的计算和证明问题.
重点难点:本节重点:熟练应用正、余弦定理解决三角形中的相关问题.
本节难点:三角形中的边角关系的建立.
课标定位
基础知识梳理
2.三角形内角和定理:_________________________.
说明:(1)正弦定理和余弦定理的主要作用:
①解三角形;
②判断三角形的形状;
③证明三角形中的恒等式.
(2)正弦定理和余弦定理的主要功能是实现三角形中边角关系的转化.
三角形的内角和是180°
课堂互动讲练
题型一
三角形的面积问题
在不同的已知条件下,求三角形面积的问题与解三角形有密切的关系,通常我们要根据已知条件,利用正弦定理、余弦定理求出需要的元素,从而求出三角形的面积.
例1
变式训练
求解最值问题,一般要把要求最值的量用一个变量表示出来,并且要确定变量的取值范围,对于三角形中的最值问题,要充分利用正、余弦定理及面积公式,运用三角函数的性质求最值.
题型二
三角形中的最值问题
已知△ABC内接于半径为R的圆中,且满足关系式2R(sin2A-sin2C)=(a-b)sinB,求△ABC面积的最大值.
【分析】 求面积的最值,应先根据条件写出面积的表达式,再根据表达式求最值.
例2
【点评】 本题综合运用正、余弦定理,把边化成角,再利用三角函数的有界性解决.
2.在△ABC中,a+b=10,且cosC是方程2x2-3x-2=0的一个根,求△ABC周长的最小值.
变式训练
在几何中有关三角函数计算、证明,平面图形的边长、面积等求解经常用到正、余弦定理.
题型三
正、余弦定理在几何计算中的应用
例3
【分析】 由条件知可以由余弦定理求出cosA的值,而要求的式子中含有sinA、tanA,故只要由sin2A+cos2A=1求出sinA即可.
【点评】 本题将余弦定理与三角求值结合在一起,解题的关键是求出cosA.
变式训练
答案:30°
规律方法总结
在解三角形问题时,一定要根据具体情况,恰当地选用正弦定理或余弦定理,公式选择得当、方法运用巧妙是简化问题的必要手段,同时还要注意与三角形的其他知识的综合运用.如:三角形内角和定理,大边对大角,两边之和大于第三边,两边之差小于第三边,三角形的面积公式等.
随堂即时巩固
课时活页训练
