【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.3第一课时
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第一章1.3第一课时 |  | |
| 格式 | rar | ||
| 文件大小 | 666.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:34:29 | ||
图片预览









文档简介
(共38张PPT)
1.3 正弦定理、余弦定理的应用
第一课时
课标要求:1.掌握利用正弦定理和余弦定理解任意三角形的基本类型和方法.
2.了解任意三角形的知识在实际中的广泛应用,能在实际问题中抽象或构造出三角形,并根据各量间的关系确定解三角形的方法.
3.初步掌握用解三角形知识解应用题的步骤和方法.
重点难点:本节重点:利用解三角形的知识解决数学建模问题.
本节难点:实际问题的数学化(建模).
课标定位
基础知识梳理
1.解三角形应用题的基本思路
解三角形应用题的关键是将____________转化为解三角形问题来解决,所以首先将实际问题抽象转化为数学问题(解三角形问题),然后利用正余弦定理对三角形进行求解,最后再回到实际问题中作答.
实际问题
2.解三角形应用问题的一般步骤
(1)准确理解题意,分清已知与所求;
(2)根据题意画出示意图或准确地理解图形;
(3)建立数学模型,
合理运用______________________________________正确求解,并作答;
(4)再根据实际问题的意义和精确度的要求给出答案.
正余弦定理和其它三角与平面几何知识
3.实际问题中的有关术语、名称
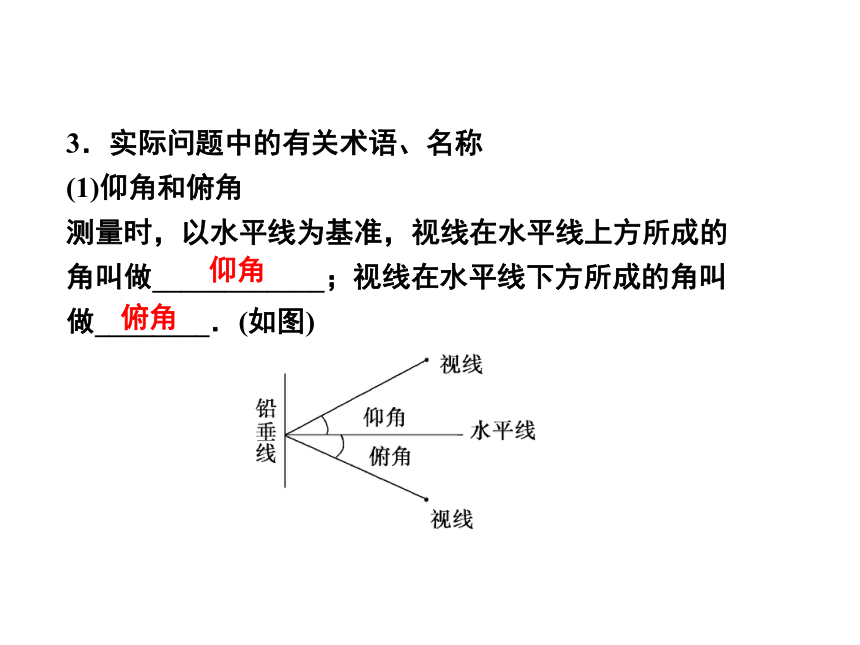
(1)仰角和俯角
测量时,以水平线为基准,视线在水平线上方所成的角叫做____________;视线在水平线下方所成的角叫做________.(如图)
仰角
俯角
(2)方向角与方位角
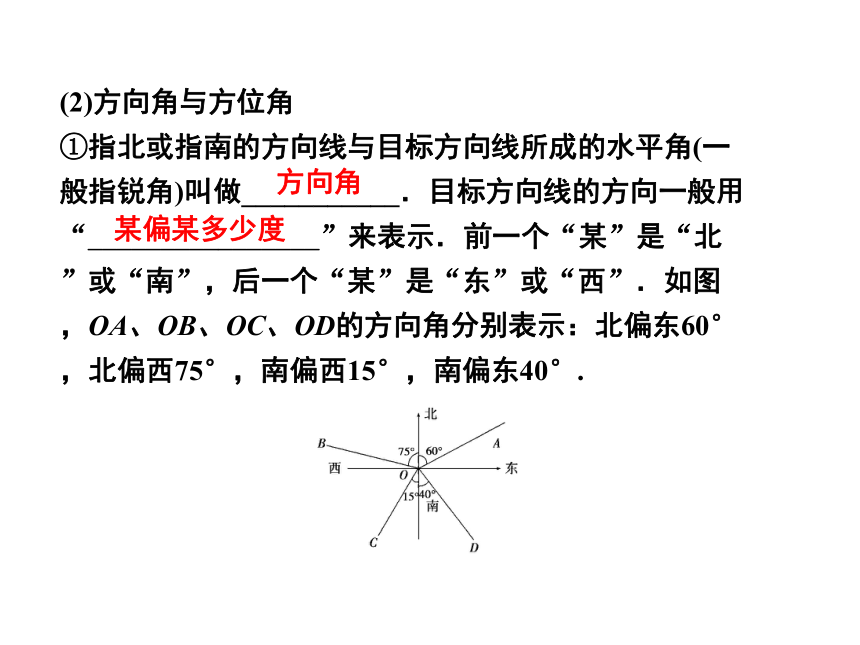
①指北或指南的方向线与目标方向线所成的水平角(一般指锐角)叫做___________.目标方向线的方向一般用“________________”来表示.前一个“某”是“北”或“南”,后一个“某”是“东”或“西”.如图,OA、OB、OC、OD的方向角分别表示:北偏东60°,北偏西75°,南偏西15°,南偏东40°.
方向角
某偏某多少度
②指北的方向线_____时针转到目标方向线为止的水平角,叫方位角.
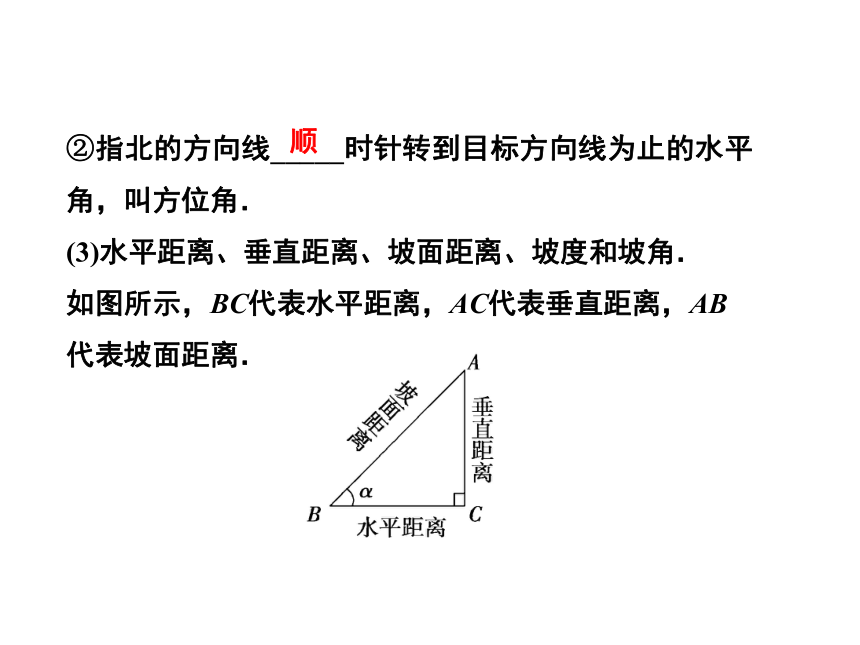
(3)水平距离、垂直距离、坡面距离、坡度和坡角.
如图所示,BC代表水平距离,AC代表垂直距离,AB代表坡面距离.
顺
课堂互动讲练
题型一
测量距离问题
测量距离问题:这类问题一般属于“测量有障碍物相隔的两点之间的距离”,在测量过程中一般要根据实际情况选取合适的基线,测量工具要有较高的精确度.
例1
【分析】 根据图中的已知条件求出一些点与点之间的距离,结合图形和计算出的距离作出判断,然后把B、D间距离的计算转化为找到的与B、D间距离相等的另外两点之间的距离.
【解】 在△ACD中,∠DAC=30°,∠ADC=60°-∠DAC=30°,
所以CD=AC=0.1.又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA.
【点评】 要计算距离就必须把这个距离归结到一个三角形中,通过正弦定理或余弦定理进行计算,但无论是正弦定理还是余弦定理都得至少知道三角形的一个边长,即在解决问题时,必须把我们已知道长度的那个边长和需要计算的那个边长纳入到同一个三角形中,或是通过间接的途径纳入到同一个三角形中,这是我们分析这类问题的一个基本出发点.
变式训练
测量高度问题:这类问题属于“测量底部或顶部不能到达的物体的高度”.测量过程中,要注意选取适量不同的测量点,使测量有较高的精确度.
题型二
测量高度问题
在平地上有A、B两点,A在山的正东,B在山的东南,且在A的南偏西25°距离A 300米的地方.在A测得山顶的仰角是30°,求山高(精确到1米).
【分析】 题中A、B、C、D不在同一平面内,首先要正确画出空间图形,将东南方向画成45°夹角.
例2
【点评】 解决上述问题首先要正确画出符合题意的示意图,然后将问题转化为解三角形的问题,即将实际问题转化为“数学模型”,这是我们解决这类问题的关键之所在.
2.为测量建造中的上海东方明珠电视塔已到达的高度,李明在学校操场的某一直线上选择A、B、C三点,AB=BC=60米,且在A、B、C三点观察塔的最高点,测得仰角分别为45°、54.2°、60°.已知李明身高1.5米,试问建造中的电视塔已到达的高度.(结果保留一位小数)
变式训练
解:根据题意画出示意图,设DE=x,则h=x+1.5.
在Rt△AED、Rt△BED、
Rt△CED中,
AE=DE·cot45°=x,
BE=DE·cot54.2°=x·cot54.2°,
测量角度问题:这类问题属于“根据需要,对某些物体定位”,测量的数据越精确,定位的精度越高.
题型三
测量角度问题
甲船在A处遇险,在甲船西南10海里B处的乙船收到甲船的报警后,测得甲船是沿着东偏北105°的方向,以每小时9海里的速度向某岛靠近,如果乙船要在40分钟内追上甲船,问乙船应以什么速度、向何方向航行?
【分析】 解答本题可先画出示意图,将问题转化为解三角形,再应用余弦定理、正弦定理求解.
例3
变式训练
规律方法总结
1.解三角形的实质是研究三角形的边角关系,涉及的知识有三角形边、角、内切圆与外接圆半径、面积,还经常联系一元二次方程、方程组及最值等.
2.将某些实际问题转化为解三角形问题,是常遇到的应用问题,解这类问题,关键是如何将实际问题转化为数学问题,画出示意图,有助于将抽象问题具体化、形象化.
3.解斜三角形在实际中的应用是很广泛的,如测量、航海、机械设计、几何、物理等方面都要运用到解三角形.
4.由于在实际测量过程中有一些误差,为了将误差控制在允许范围内,我们往往要对同一对象测量多次,然后取它们的平均值作为所得的测量数据,在实际问题的计算中,有一定的精度要求,要注意近似计算法则,以严谨细致的科学态度求出测量结果.
随堂即时巩固
课时活页训练
1.3 正弦定理、余弦定理的应用
第一课时
课标要求:1.掌握利用正弦定理和余弦定理解任意三角形的基本类型和方法.
2.了解任意三角形的知识在实际中的广泛应用,能在实际问题中抽象或构造出三角形,并根据各量间的关系确定解三角形的方法.
3.初步掌握用解三角形知识解应用题的步骤和方法.
重点难点:本节重点:利用解三角形的知识解决数学建模问题.
本节难点:实际问题的数学化(建模).
课标定位
基础知识梳理
1.解三角形应用题的基本思路
解三角形应用题的关键是将____________转化为解三角形问题来解决,所以首先将实际问题抽象转化为数学问题(解三角形问题),然后利用正余弦定理对三角形进行求解,最后再回到实际问题中作答.
实际问题
2.解三角形应用问题的一般步骤
(1)准确理解题意,分清已知与所求;
(2)根据题意画出示意图或准确地理解图形;
(3)建立数学模型,
合理运用______________________________________正确求解,并作答;
(4)再根据实际问题的意义和精确度的要求给出答案.
正余弦定理和其它三角与平面几何知识
3.实际问题中的有关术语、名称
(1)仰角和俯角
测量时,以水平线为基准,视线在水平线上方所成的角叫做____________;视线在水平线下方所成的角叫做________.(如图)
仰角
俯角
(2)方向角与方位角
①指北或指南的方向线与目标方向线所成的水平角(一般指锐角)叫做___________.目标方向线的方向一般用“________________”来表示.前一个“某”是“北”或“南”,后一个“某”是“东”或“西”.如图,OA、OB、OC、OD的方向角分别表示:北偏东60°,北偏西75°,南偏西15°,南偏东40°.
方向角
某偏某多少度
②指北的方向线_____时针转到目标方向线为止的水平角,叫方位角.
(3)水平距离、垂直距离、坡面距离、坡度和坡角.
如图所示,BC代表水平距离,AC代表垂直距离,AB代表坡面距离.
顺
课堂互动讲练
题型一
测量距离问题
测量距离问题:这类问题一般属于“测量有障碍物相隔的两点之间的距离”,在测量过程中一般要根据实际情况选取合适的基线,测量工具要有较高的精确度.
例1
【分析】 根据图中的已知条件求出一些点与点之间的距离,结合图形和计算出的距离作出判断,然后把B、D间距离的计算转化为找到的与B、D间距离相等的另外两点之间的距离.
【解】 在△ACD中,∠DAC=30°,∠ADC=60°-∠DAC=30°,
所以CD=AC=0.1.又∠BCD=180°-60°-60°=60°,
故CB是△CAD底边AD的中垂线,所以BD=BA.
【点评】 要计算距离就必须把这个距离归结到一个三角形中,通过正弦定理或余弦定理进行计算,但无论是正弦定理还是余弦定理都得至少知道三角形的一个边长,即在解决问题时,必须把我们已知道长度的那个边长和需要计算的那个边长纳入到同一个三角形中,或是通过间接的途径纳入到同一个三角形中,这是我们分析这类问题的一个基本出发点.
变式训练
测量高度问题:这类问题属于“测量底部或顶部不能到达的物体的高度”.测量过程中,要注意选取适量不同的测量点,使测量有较高的精确度.
题型二
测量高度问题
在平地上有A、B两点,A在山的正东,B在山的东南,且在A的南偏西25°距离A 300米的地方.在A测得山顶的仰角是30°,求山高(精确到1米).
【分析】 题中A、B、C、D不在同一平面内,首先要正确画出空间图形,将东南方向画成45°夹角.
例2
【点评】 解决上述问题首先要正确画出符合题意的示意图,然后将问题转化为解三角形的问题,即将实际问题转化为“数学模型”,这是我们解决这类问题的关键之所在.
2.为测量建造中的上海东方明珠电视塔已到达的高度,李明在学校操场的某一直线上选择A、B、C三点,AB=BC=60米,且在A、B、C三点观察塔的最高点,测得仰角分别为45°、54.2°、60°.已知李明身高1.5米,试问建造中的电视塔已到达的高度.(结果保留一位小数)
变式训练
解:根据题意画出示意图,设DE=x,则h=x+1.5.
在Rt△AED、Rt△BED、
Rt△CED中,
AE=DE·cot45°=x,
BE=DE·cot54.2°=x·cot54.2°,
测量角度问题:这类问题属于“根据需要,对某些物体定位”,测量的数据越精确,定位的精度越高.
题型三
测量角度问题
甲船在A处遇险,在甲船西南10海里B处的乙船收到甲船的报警后,测得甲船是沿着东偏北105°的方向,以每小时9海里的速度向某岛靠近,如果乙船要在40分钟内追上甲船,问乙船应以什么速度、向何方向航行?
【分析】 解答本题可先画出示意图,将问题转化为解三角形,再应用余弦定理、正弦定理求解.
例3
变式训练
规律方法总结
1.解三角形的实质是研究三角形的边角关系,涉及的知识有三角形边、角、内切圆与外接圆半径、面积,还经常联系一元二次方程、方程组及最值等.
2.将某些实际问题转化为解三角形问题,是常遇到的应用问题,解这类问题,关键是如何将实际问题转化为数学问题,画出示意图,有助于将抽象问题具体化、形象化.
3.解斜三角形在实际中的应用是很广泛的,如测量、航海、机械设计、几何、物理等方面都要运用到解三角形.
4.由于在实际测量过程中有一些误差,为了将误差控制在允许范围内,我们往往要对同一对象测量多次,然后取它们的平均值作为所得的测量数据,在实际问题的计算中,有一定的精度要求,要注意近似计算法则,以严谨细致的科学态度求出测量结果.
随堂即时巩固
课时活页训练
