五年级上册数学教案-2.6 运用平移知识解决面积问题 西师大版
文档属性
| 名称 | 五年级上册数学教案-2.6 运用平移知识解决面积问题 西师大版 |  | |
| 格式 | doc | ||
| 文件大小 | 699.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 17:42:23 | ||
图片预览

文档简介
运用平移知识解决面积问题
教学内容:
教学目标:
让学生经历自主探究的过程,运用平移的方法解决不规则的面积问题,加深对“平移” 这种图形变换方式的理解。
在解决简单不规则图形面积问题的过程中,培养学生迁移、转化的能力,发展空间观念。
体会数学知识间的密切联系,感受数学美。
教学重点:运用平移的方法解决简单不规则图形的面积问题。
教学难点:在解决问题的过程中,加深对平移的理解。
教学过程
情境导入
师:同学们,你听说过曹冲称象的故事吗?(听说过)让我们重温曹冲聪明的做法吧!
(播放视频:曹冲称象)
师:称大象体重容易吗?
生:不容易。
师:最后称的是什么呢?
生:石头。
师:大象的体重等于石头的重量?
生:是。
师:大象是一个整体,石头是局部。这里运用了整体转化为局部的思想。从而巧妙的解决称大象的难题,真是有志不在年高,了不起,相信同学们通过今天的学习也会有不俗的表现。
师:这是一个花台的平面图 。(出示图形)
880110127635
师 :想要求它的面积好求吗?
生:不好求。
师:我也觉得不好求。可不可以放进方格图里?
探究交流
师:老师把这个花台模型放到边长为1m的方格图中。16478251708151m
1m
54991087630
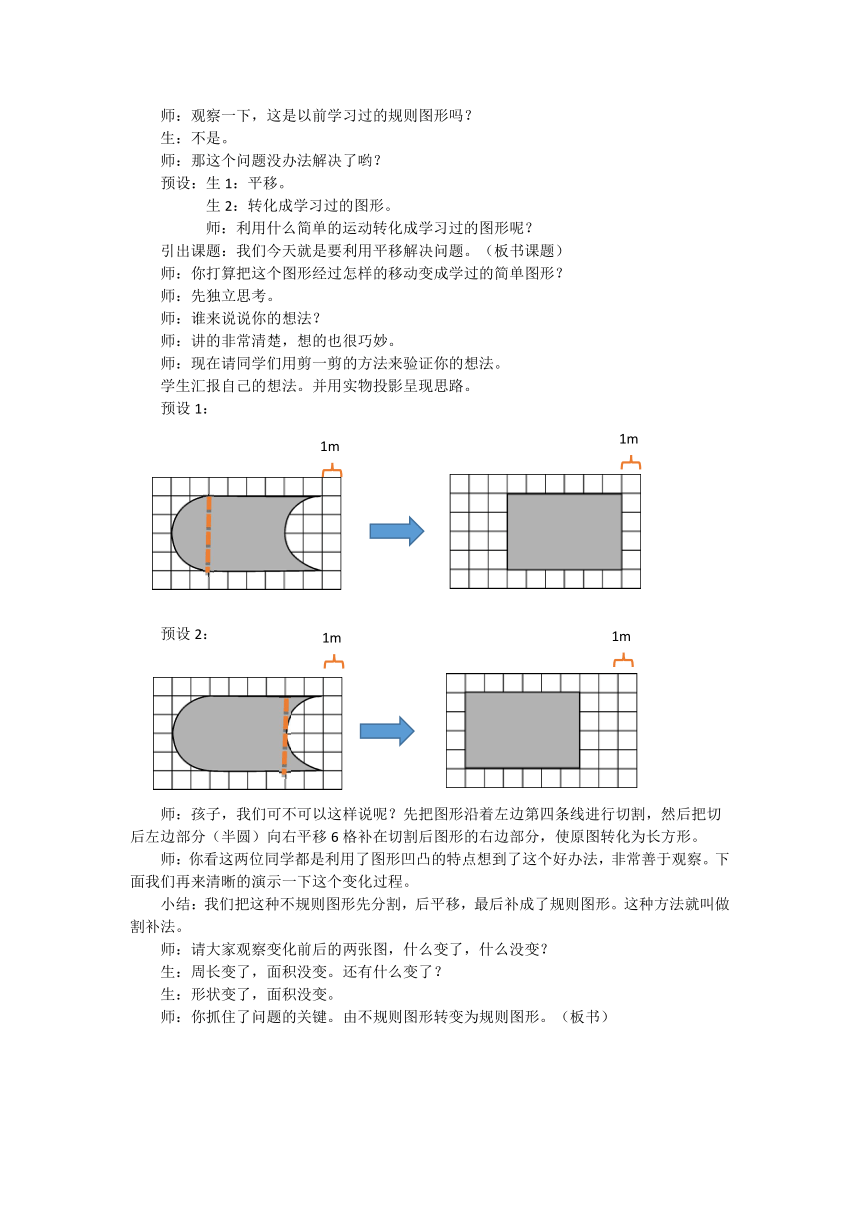
师:观察一下,这是以前学习过的规则图形吗?
生:不是。
师:那这个问题没办法解决了哟?
预设:生1:平移。
生2:转化成学习过的图形。
师:利用什么简单的运动转化成学习过的图形呢?
引出课题:我们今天就是要利用平移解决问题。(板书课题)
师:你打算把这个图形经过怎样的移动变成学过的简单图形?
师:先独立思考。
师:谁来说说你的想法?
师:讲的非常清楚,想的也很巧妙。
师:现在请同学们用剪一剪的方法来验证你的想法。
学生汇报自己的想法。并用实物投影呈现思路。
预设1:
3936365171451m
1m
1309370850901m
1m
4216401981201cm
1cm
1936751111256845302832102112645463550
38703251695451m
1m
13258801828801m
1m
预设2:
27806655715020701087630
135128076200
202692042545
师:孩子,我们可不可以这样说呢?先把图形沿着左边第四条线进行切割,然后把切
后左边部分(半圆)向右平移6格补在切割后图形的右边部分,使原图转化为长方形。
师:你看这两位同学都是利用了图形凹凸的特点想到了这个好办法,非常善于观察。下面我们再来清晰的演示一下这个变化过程。
小结:我们把这种不规则图形先分割,后平移,最后补成了规则图形。这种方法就叫做割补法。
师:请大家观察变化前后的两张图,什么变了,什么没变?
生:周长变了,面积没变。还有什么变了?
生:形状变了,面积没变。
师:你抓住了问题的关键。由不规则图形转变为规则图形。(板书)
3893185933451m
1m
1315085457201m
1m
2757805173355203200189865
687705160655
2148840110490
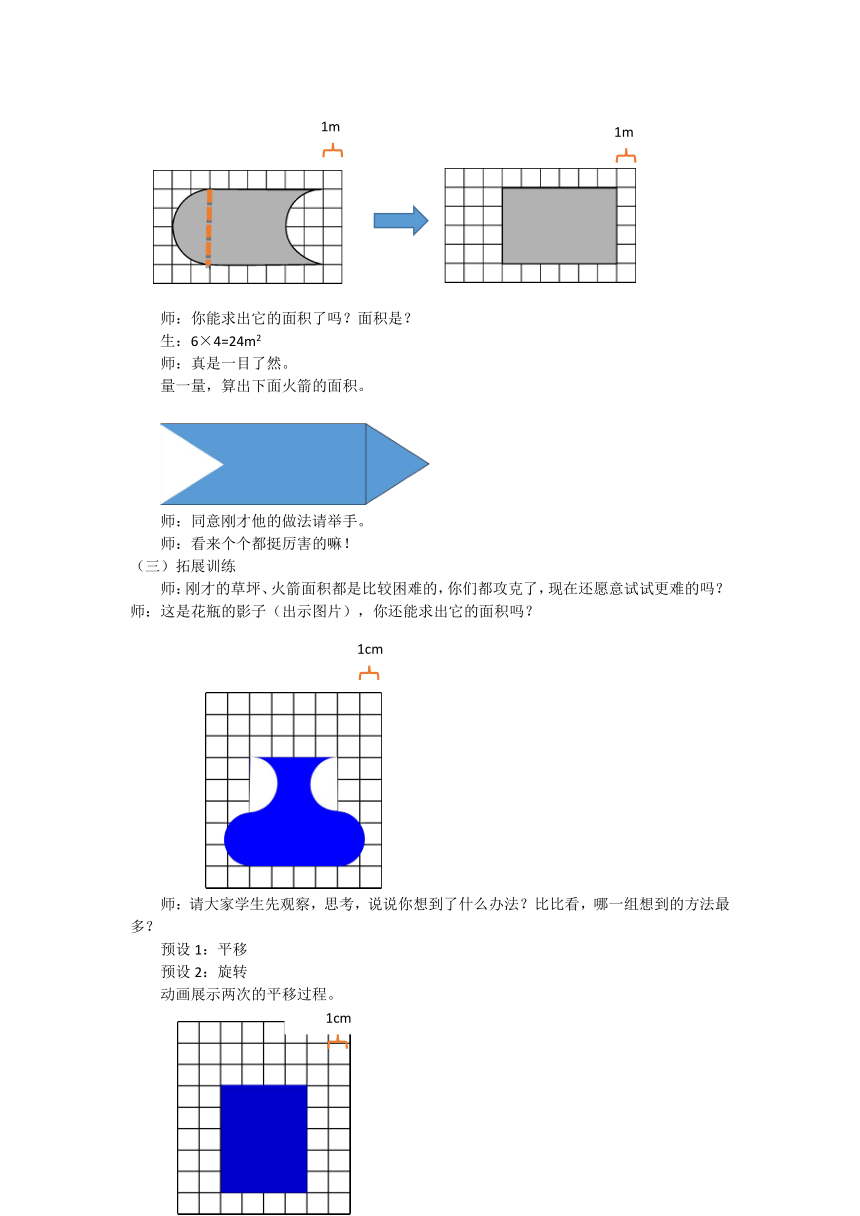
师:你能求出它的面积了吗?面积是?
生:6×4=24m2
师:真是一目了然。
量一量,算出下面火箭的面积。
师:同意刚才他的做法请举手。
师:看来个个都挺厉害的嘛!
拓展训练
师:刚才的草坪、火箭面积都是比较困难的,你们都攻克了,现在还愿意试试更难的吗?师:这是花瓶的影子(出示图片),你还能求出它的面积吗?
1634490850901cm
1cm
师:请大家学生先观察,思考,说说你想到了什么办法?比比看,哪一组想到的方法最多?
预设1:平移
预设2:旋转
13576301581151cm
1cm
动画展示两次的平移过程。
41592574295
师:现在你能解决它的面积是多少了吗?
生:5×4=20cm2
(四)巩固练习,灵活运用
1.涂色部分占整个图形的几分之几?
220027567945
23088601803401cm
1cm
2.想一想,怎样才能算出下面图形的周长?
师:这个图形的周长可有难度了,你有什么好方法,能既准确有快速地算出这个图形的周长呢?
学生独立解决问题,教师巡查,了解学生解决问题情况。
学生边指边说想法。
师:你是想把这四条边平移是吗?大家来看,他是把这个图形想象成了什么?(长方形)能行吗?我们来看一下。真像大家想象的那样,这是把什么转化成什么?
生:把不规则图形转化成长方形。
师:这样转化什么变了,什么没变?
生:面积变了,周长没变。
师:还有要补充的吗?形状也变了。
师:咱们同学不仅会观察,还很会想象。我们在用转化策略解决问题的时候观察很重要,想象也很重要。感受到用转化策略解决问题的乐趣了没有?
(五)课堂小结,提升认识
师:这节课我们用转化的策略解决了一些不规则图形的面积问题。
555625130175
师:通过今天的研究探索,你有哪些收获?
学生交流。
师:看来,大家的收获真不少,最后,有一句话想与同学们分享分享。
出示:
“天下难事,必作于易;天下大事,必作于细”。 ——思想家老子
师:从今天学习转化策略的角度,你能明白它们的含义吗?
作业
必做题:
5270503124201m{
1m{
想一想,怎样才能算出下面菜地的周长。
198120019685
2、涂色部分占整个图形的几分之几?
3、下图是两个边长是4米的正方形拼成的图形,求下图阴影部分面积。
选做题:
1、求阴影部分的面积。
1085851246505 1085851246505
教学内容:
教学目标:
让学生经历自主探究的过程,运用平移的方法解决不规则的面积问题,加深对“平移” 这种图形变换方式的理解。
在解决简单不规则图形面积问题的过程中,培养学生迁移、转化的能力,发展空间观念。
体会数学知识间的密切联系,感受数学美。
教学重点:运用平移的方法解决简单不规则图形的面积问题。
教学难点:在解决问题的过程中,加深对平移的理解。
教学过程
情境导入
师:同学们,你听说过曹冲称象的故事吗?(听说过)让我们重温曹冲聪明的做法吧!
(播放视频:曹冲称象)
师:称大象体重容易吗?
生:不容易。
师:最后称的是什么呢?
生:石头。
师:大象的体重等于石头的重量?
生:是。
师:大象是一个整体,石头是局部。这里运用了整体转化为局部的思想。从而巧妙的解决称大象的难题,真是有志不在年高,了不起,相信同学们通过今天的学习也会有不俗的表现。
师:这是一个花台的平面图 。(出示图形)
880110127635
师 :想要求它的面积好求吗?
生:不好求。
师:我也觉得不好求。可不可以放进方格图里?
探究交流
师:老师把这个花台模型放到边长为1m的方格图中。16478251708151m
1m
54991087630
师:观察一下,这是以前学习过的规则图形吗?
生:不是。
师:那这个问题没办法解决了哟?
预设:生1:平移。
生2:转化成学习过的图形。
师:利用什么简单的运动转化成学习过的图形呢?
引出课题:我们今天就是要利用平移解决问题。(板书课题)
师:你打算把这个图形经过怎样的移动变成学过的简单图形?
师:先独立思考。
师:谁来说说你的想法?
师:讲的非常清楚,想的也很巧妙。
师:现在请同学们用剪一剪的方法来验证你的想法。
学生汇报自己的想法。并用实物投影呈现思路。
预设1:
3936365171451m
1m
1309370850901m
1m
4216401981201cm
1cm
1936751111256845302832102112645463550
38703251695451m
1m
13258801828801m
1m
预设2:
27806655715020701087630
135128076200
202692042545
师:孩子,我们可不可以这样说呢?先把图形沿着左边第四条线进行切割,然后把切
后左边部分(半圆)向右平移6格补在切割后图形的右边部分,使原图转化为长方形。
师:你看这两位同学都是利用了图形凹凸的特点想到了这个好办法,非常善于观察。下面我们再来清晰的演示一下这个变化过程。
小结:我们把这种不规则图形先分割,后平移,最后补成了规则图形。这种方法就叫做割补法。
师:请大家观察变化前后的两张图,什么变了,什么没变?
生:周长变了,面积没变。还有什么变了?
生:形状变了,面积没变。
师:你抓住了问题的关键。由不规则图形转变为规则图形。(板书)
3893185933451m
1m
1315085457201m
1m
2757805173355203200189865
687705160655
2148840110490
师:你能求出它的面积了吗?面积是?
生:6×4=24m2
师:真是一目了然。
量一量,算出下面火箭的面积。
师:同意刚才他的做法请举手。
师:看来个个都挺厉害的嘛!
拓展训练
师:刚才的草坪、火箭面积都是比较困难的,你们都攻克了,现在还愿意试试更难的吗?师:这是花瓶的影子(出示图片),你还能求出它的面积吗?
1634490850901cm
1cm
师:请大家学生先观察,思考,说说你想到了什么办法?比比看,哪一组想到的方法最多?
预设1:平移
预设2:旋转
13576301581151cm
1cm
动画展示两次的平移过程。
41592574295
师:现在你能解决它的面积是多少了吗?
生:5×4=20cm2
(四)巩固练习,灵活运用
1.涂色部分占整个图形的几分之几?
220027567945
23088601803401cm
1cm
2.想一想,怎样才能算出下面图形的周长?
师:这个图形的周长可有难度了,你有什么好方法,能既准确有快速地算出这个图形的周长呢?
学生独立解决问题,教师巡查,了解学生解决问题情况。
学生边指边说想法。
师:你是想把这四条边平移是吗?大家来看,他是把这个图形想象成了什么?(长方形)能行吗?我们来看一下。真像大家想象的那样,这是把什么转化成什么?
生:把不规则图形转化成长方形。
师:这样转化什么变了,什么没变?
生:面积变了,周长没变。
师:还有要补充的吗?形状也变了。
师:咱们同学不仅会观察,还很会想象。我们在用转化策略解决问题的时候观察很重要,想象也很重要。感受到用转化策略解决问题的乐趣了没有?
(五)课堂小结,提升认识
师:这节课我们用转化的策略解决了一些不规则图形的面积问题。
555625130175
师:通过今天的研究探索,你有哪些收获?
学生交流。
师:看来,大家的收获真不少,最后,有一句话想与同学们分享分享。
出示:
“天下难事,必作于易;天下大事,必作于细”。 ——思想家老子
师:从今天学习转化策略的角度,你能明白它们的含义吗?
作业
必做题:
5270503124201m{
1m{
想一想,怎样才能算出下面菜地的周长。
198120019685
2、涂色部分占整个图形的几分之几?
3、下图是两个边长是4米的正方形拼成的图形,求下图阴影部分面积。
选做题:
1、求阴影部分的面积。
1085851246505 1085851246505
