【2012优化方案 精品课件】苏教版 数学 必修5:第二章2.2.3第二课时
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第二章2.2.3第二课时 |  | |
| 格式 | rar | ||
| 文件大小 | 526.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:34:29 | ||
图片预览



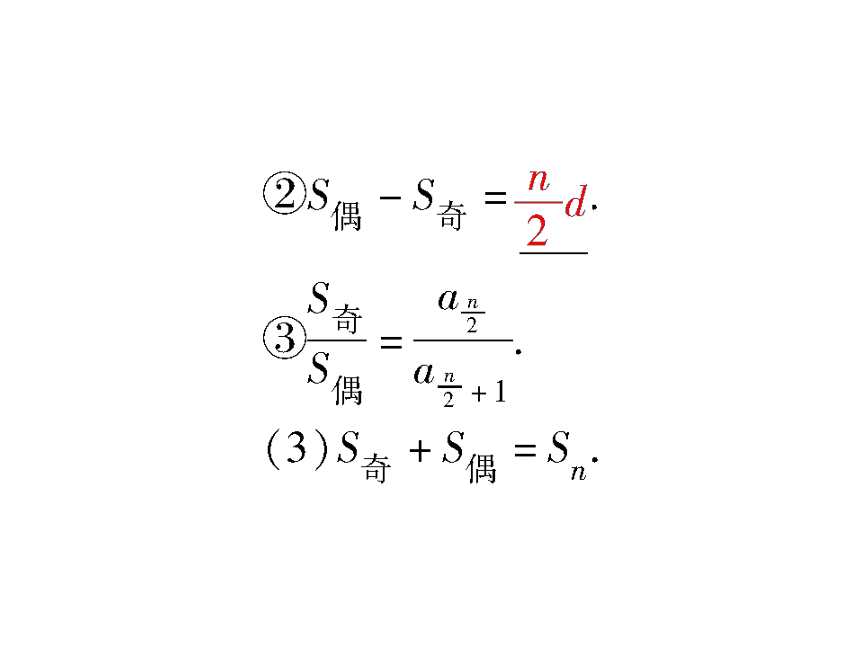






文档简介
(共32张PPT)
第二课时
课标要求:1.掌握与和有关的等差数列的一些常用性质.
2.应用通项公式及求和公式等解决一些等差数列的问题,提高综合能力.
重点难点:本节重点:等差数列求和的有关性质及应用.
本节难点:等差数列的性质与公式的综合运用及变形技巧.
课标定位
基础知识梳理
n2d
课堂互动讲练
题型一
等差数列前n项和公式的性质
此类问题考察的主要是等差数列前n项和公式的性质的灵活应用.
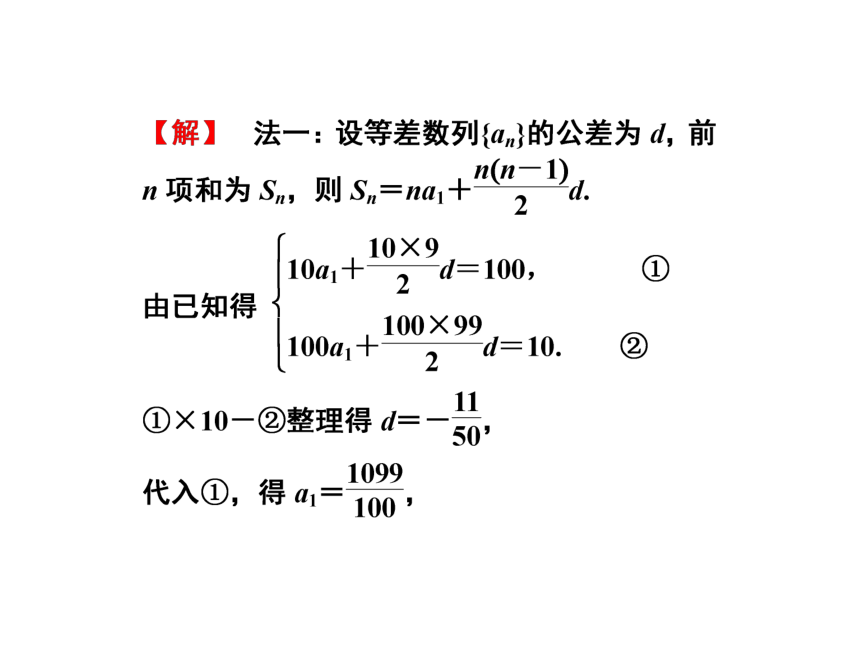
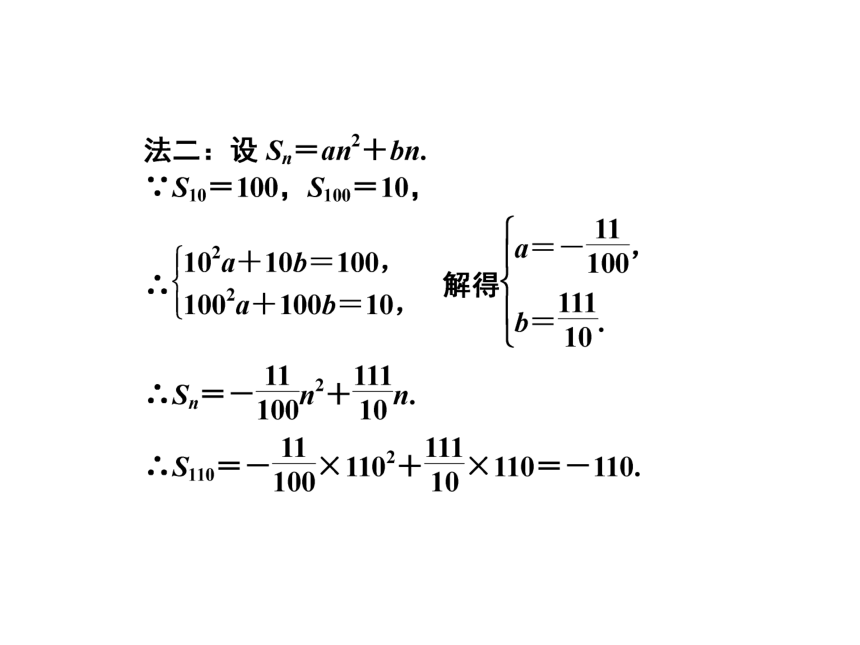
等差数列{an}中,S10=100,S100=10,求S110.
【分析】 可由等差数列的前n项和公式求解,也可由等差数列前n项和的性质,即等差数列中,Sm,S2m-Sm,S3m-S2m成等差数列求解.
【点评】 由本题可得到求等差数列前n项和的常用方法:(1)直接代入公式,列方程组求解;(2)灵活运用等差数列前n项和的性质;(3)利用前n项和的二次函数性质.
1.一个等差数列前12项的和为354,其中项数为偶数的项的和与项数为奇数的项的和之比为32∶27,求公差d.
变式训练
题型二
等差数列前n项的和的最值问题
例2
【点评】 (1)对于本题,也可先由an≥0求得n的值,再代入前n项和公式求最值.
(2)根据项的值判断前n项和的最值有以下结论:
①当a1>0,d>0时,a1<a2<a3<…<an<an+1<…,则S1最小;
②当a1>0,d<0时,a1>a2>a3>…>an>0≥an+1>…,则Sn最大;
③当a1<0,d>0时,a1<a2<a3<…<an<0≤an+1<…,则Sn最小;
④当a1<0,d<0时,a1>a2>a3>…>an>an+1>…,则S1最大.
2.(2010年高考课标全国卷)设等差数列{an}满足a3=5,a10=-9.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn及使得Sn最大的序号n的值.
变式训练
解决好这类应用题的关键在于找准数列模型.
某工厂从今年起,若不改善生产环境,按现状生产,每月收入为70万元,同时将受到环保部门的处罚,第一个月罚3万元,以后每月递增2万元.如果从今年一月起投资400万元增加回收净化设备以改善生产环境(改造设备时间不计).按测算,新设备投产后的月收入与时间的关系如图所示.
题型三
等差数列前n项和公式在实际生活中的应用
例3
(1)设g(n)表示投资改造后的前n个月的总收入,写出g(n)的函数关系式;
(2)问经过多少个月,投资开始见效,即投资改造后的月累计纯收入多于不改造时的月累计纯收入?
【分析】 由图形可知,投资改造后的前n个月的收入分别是(单位:万元)
101,103,105,107,109,109,…
它的前五项是公差为2的等差数列,从第六项开始是常数列,g(n)表示这个数列的前n项和,应分n≤5和n>5两种情形讨论.而不改造时的前n个月收入分别是(单位:万元):67,65,63,…,69-2n,…,累计纯收入即为该等差数列的前n项的和:Sn=68n-n2,投资改造后的前n个月累计纯收入为g(n)-400,解不等式g(n)-400>Sn=68n-n2,求n.
【点评】 通过图象深刻考查学生对数列概念及表示法的理解和运用,检验学生对文字语言、数学符号语言、图形语言之间的阅读理解能力及其相互转换能力.
3.一个水池有若干出水量相同的水龙头,如果所有水龙头同时放水,那么24 min可注满水池.如果开始时全部放开,以后每隔相等的时间关闭一个水龙头,到最后一个水龙头关闭时,恰好注满水池,而且最后一个水龙头放水的时间恰好是第一个水龙头放水时间的5倍,问最后关闭的这个水龙头放水多长时间?
变式训练
规律方法总结
随堂即时巩固
课时活页训练
第二课时
课标要求:1.掌握与和有关的等差数列的一些常用性质.
2.应用通项公式及求和公式等解决一些等差数列的问题,提高综合能力.
重点难点:本节重点:等差数列求和的有关性质及应用.
本节难点:等差数列的性质与公式的综合运用及变形技巧.
课标定位
基础知识梳理
n2d
课堂互动讲练
题型一
等差数列前n项和公式的性质
此类问题考察的主要是等差数列前n项和公式的性质的灵活应用.
等差数列{an}中,S10=100,S100=10,求S110.
【分析】 可由等差数列的前n项和公式求解,也可由等差数列前n项和的性质,即等差数列中,Sm,S2m-Sm,S3m-S2m成等差数列求解.
【点评】 由本题可得到求等差数列前n项和的常用方法:(1)直接代入公式,列方程组求解;(2)灵活运用等差数列前n项和的性质;(3)利用前n项和的二次函数性质.
1.一个等差数列前12项的和为354,其中项数为偶数的项的和与项数为奇数的项的和之比为32∶27,求公差d.
变式训练
题型二
等差数列前n项的和的最值问题
例2
【点评】 (1)对于本题,也可先由an≥0求得n的值,再代入前n项和公式求最值.
(2)根据项的值判断前n项和的最值有以下结论:
①当a1>0,d>0时,a1<a2<a3<…<an<an+1<…,则S1最小;
②当a1>0,d<0时,a1>a2>a3>…>an>0≥an+1>…,则Sn最大;
③当a1<0,d>0时,a1<a2<a3<…<an<0≤an+1<…,则Sn最小;
④当a1<0,d<0时,a1>a2>a3>…>an>an+1>…,则S1最大.
2.(2010年高考课标全国卷)设等差数列{an}满足a3=5,a10=-9.
(1)求{an}的通项公式;
(2)求{an}的前n项和Sn及使得Sn最大的序号n的值.
变式训练
解决好这类应用题的关键在于找准数列模型.
某工厂从今年起,若不改善生产环境,按现状生产,每月收入为70万元,同时将受到环保部门的处罚,第一个月罚3万元,以后每月递增2万元.如果从今年一月起投资400万元增加回收净化设备以改善生产环境(改造设备时间不计).按测算,新设备投产后的月收入与时间的关系如图所示.
题型三
等差数列前n项和公式在实际生活中的应用
例3
(1)设g(n)表示投资改造后的前n个月的总收入,写出g(n)的函数关系式;
(2)问经过多少个月,投资开始见效,即投资改造后的月累计纯收入多于不改造时的月累计纯收入?
【分析】 由图形可知,投资改造后的前n个月的收入分别是(单位:万元)
101,103,105,107,109,109,…
它的前五项是公差为2的等差数列,从第六项开始是常数列,g(n)表示这个数列的前n项和,应分n≤5和n>5两种情形讨论.而不改造时的前n个月收入分别是(单位:万元):67,65,63,…,69-2n,…,累计纯收入即为该等差数列的前n项的和:Sn=68n-n2,投资改造后的前n个月累计纯收入为g(n)-400,解不等式g(n)-400>Sn=68n-n2,求n.
【点评】 通过图象深刻考查学生对数列概念及表示法的理解和运用,检验学生对文字语言、数学符号语言、图形语言之间的阅读理解能力及其相互转换能力.
3.一个水池有若干出水量相同的水龙头,如果所有水龙头同时放水,那么24 min可注满水池.如果开始时全部放开,以后每隔相等的时间关闭一个水龙头,到最后一个水龙头关闭时,恰好注满水池,而且最后一个水龙头放水的时间恰好是第一个水龙头放水时间的5倍,问最后关闭的这个水龙头放水多长时间?
变式训练
规律方法总结
随堂即时巩固
课时活页训练
