【2012优化方案 精品课件】苏教版 数学 必修5:第二章2.3.2
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第二章2.3.2 |

|
|
| 格式 | rar | ||
| 文件大小 | 836.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:34:29 | ||
图片预览










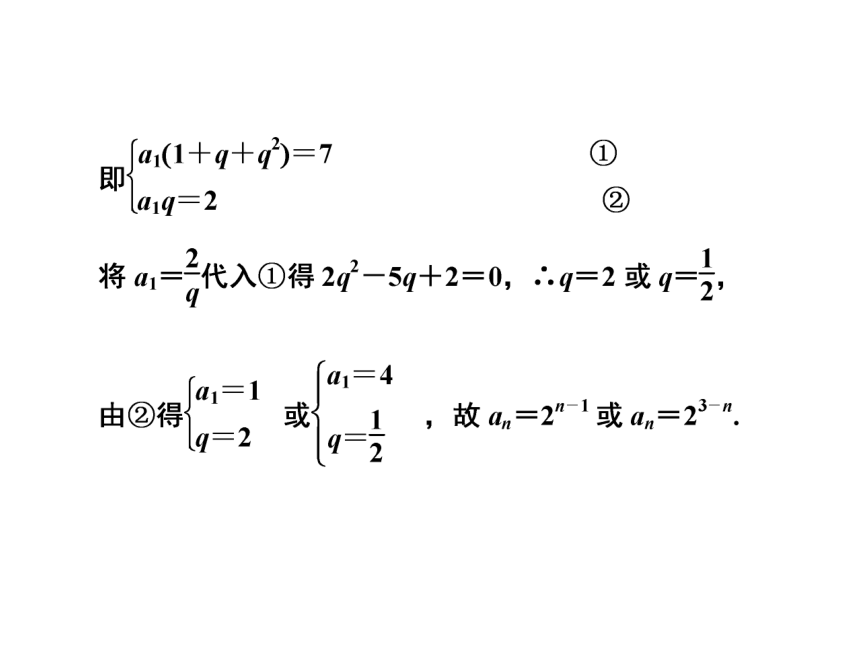

文档简介
(共31张PPT)
2.3.2 等比数列的通项公式
课标要求:1.掌握等比数列的通项公式,能运用公式解决一些简单的问题.
2.能在具体的问题情境中,发现数列的等比关系,并能用有关知识解决相应的问题.
3.了解等比数列与指数函数的关系.
课标定位
重点难点:本节重点:等比数列的通项公式的推导和应用.
本节难点:1.等比数列的通项公式的推导过程的理解和掌握.
2.与等比数列的通项公式相关的性质的灵活运用.
基础知识梳理
1.等比数列的通项公式
(1)通项公式:设数列{an}是首项为a1,公比为q的等比数列,则数列{an}的通项公式为___________.
说明:在an=a1qn-1中有a1,q,n,an四个量,知道三个可求一个.
(2)通项公式的两个变形
an=a1qn-1
qn-m
2.等比数列的性质
(1)设数列{an}为等比数列,且m,n,s,t∈N*.
①若m+n=s+t,则am·an=as·at;
②若m+n=2s,则__________.
(2)设数列{an}为等比数列,公比q≠±1,且m,n,s, t∈N*.
①若aman=asat,则m+n=s+t;
②若aman=a,则m+n=2s.
课堂互动讲练
题型一
等比数列的通项公式
已知等比数列{an},若a1+a2+a3=7,a1a2a3=8,求an.
【分析】 解答本题时,可将条件转化为关于基本元素a1与q的方程组,求出a1与q后,再表示其他量.
例1
【点评】 a1和q是等比数列的基本量,只要求出这两个基本量,其他量便可求出来,法一是常规解法,先求a1,q,再求an,法二是运用通项公式及方程思想建立方程组求a1和q,也是常见的方法.
变式训练
例2
【点评】 观察数列的递推公式,并对它进行适当的变形,构造辅助数列,使问题转化为熟悉的等比数列问题.
变式训练
证明:(1)an+1=Sn+1-Sn=4an-4an-1,
∴an+1-2an=2(an-2an-1),
∴bn=2bn-1(n≥2).
又b1=a2-2a1=S2-3a1=a1+2=3,
∴{bn}是以首项为3,公比为2的等比数列.
题型二
等比数列的判定
例3
【分析】 可先求出an,再利用等比数列的定义证明
【证明】 ∵a1+a2+…+an=2n-1, ①
∴a1=1且a1+a2+…+an-1=2n-1-1. ②
①-②,得an=2n-1(n≥2).
又a1=1,
【点评】 本题中的条件a1+a2+…+an=2n-1,即为Sn=2n-1,利用an=Sn-Sn-1可求an,但要注意验证n=1的情况.由于能先求出通项公式,因而可用定义证明.
变式训练
3.已知数列{an}中,a1=1,an+2an-1+3=0(n≥2).
(1)判断数列{an+1}是否为等比数列?并说明理由.
(2)求an.
解:(1)数列{an+1}是等比数列,证明如下:
∵a1=1,an+2an-1+3=0,∴an+1=-2(an-1+1).
∴数列{an+1}是首项为2,公比为-2的等比数列.
(2)由(1)可知an+1=2·(-2)n-1=-(-2)n.
∴an=-(-2)n-1.
题型三
等比数列的性质及应用
例4
已知等比数列{an}中,a2a6a10=1,求a3·a9.
【分析】 解答本题可以运用等比数列下标与项的运算关系,也可以利用通项公式计算.
【点评】 等比数列中的项的序号若成等差数列,则对应的项依次成等比数列,有关等比数列的计算问题,应充分发挥项的“下标”的“指引”作用,以使运算简便.
规律方法总结
随堂即时巩固
课时活页训练
2.3.2 等比数列的通项公式
课标要求:1.掌握等比数列的通项公式,能运用公式解决一些简单的问题.
2.能在具体的问题情境中,发现数列的等比关系,并能用有关知识解决相应的问题.
3.了解等比数列与指数函数的关系.
课标定位
重点难点:本节重点:等比数列的通项公式的推导和应用.
本节难点:1.等比数列的通项公式的推导过程的理解和掌握.
2.与等比数列的通项公式相关的性质的灵活运用.
基础知识梳理
1.等比数列的通项公式
(1)通项公式:设数列{an}是首项为a1,公比为q的等比数列,则数列{an}的通项公式为___________.
说明:在an=a1qn-1中有a1,q,n,an四个量,知道三个可求一个.
(2)通项公式的两个变形
an=a1qn-1
qn-m
2.等比数列的性质
(1)设数列{an}为等比数列,且m,n,s,t∈N*.
①若m+n=s+t,则am·an=as·at;
②若m+n=2s,则__________.
(2)设数列{an}为等比数列,公比q≠±1,且m,n,s, t∈N*.
①若aman=asat,则m+n=s+t;
②若aman=a,则m+n=2s.
课堂互动讲练
题型一
等比数列的通项公式
已知等比数列{an},若a1+a2+a3=7,a1a2a3=8,求an.
【分析】 解答本题时,可将条件转化为关于基本元素a1与q的方程组,求出a1与q后,再表示其他量.
例1
【点评】 a1和q是等比数列的基本量,只要求出这两个基本量,其他量便可求出来,法一是常规解法,先求a1,q,再求an,法二是运用通项公式及方程思想建立方程组求a1和q,也是常见的方法.
变式训练
例2
【点评】 观察数列的递推公式,并对它进行适当的变形,构造辅助数列,使问题转化为熟悉的等比数列问题.
变式训练
证明:(1)an+1=Sn+1-Sn=4an-4an-1,
∴an+1-2an=2(an-2an-1),
∴bn=2bn-1(n≥2).
又b1=a2-2a1=S2-3a1=a1+2=3,
∴{bn}是以首项为3,公比为2的等比数列.
题型二
等比数列的判定
例3
【分析】 可先求出an,再利用等比数列的定义证明
【证明】 ∵a1+a2+…+an=2n-1, ①
∴a1=1且a1+a2+…+an-1=2n-1-1. ②
①-②,得an=2n-1(n≥2).
又a1=1,
【点评】 本题中的条件a1+a2+…+an=2n-1,即为Sn=2n-1,利用an=Sn-Sn-1可求an,但要注意验证n=1的情况.由于能先求出通项公式,因而可用定义证明.
变式训练
3.已知数列{an}中,a1=1,an+2an-1+3=0(n≥2).
(1)判断数列{an+1}是否为等比数列?并说明理由.
(2)求an.
解:(1)数列{an+1}是等比数列,证明如下:
∵a1=1,an+2an-1+3=0,∴an+1=-2(an-1+1).
∴数列{an+1}是首项为2,公比为-2的等比数列.
(2)由(1)可知an+1=2·(-2)n-1=-(-2)n.
∴an=-(-2)n-1.
题型三
等比数列的性质及应用
例4
已知等比数列{an}中,a2a6a10=1,求a3·a9.
【分析】 解答本题可以运用等比数列下标与项的运算关系,也可以利用通项公式计算.
【点评】 等比数列中的项的序号若成等差数列,则对应的项依次成等比数列,有关等比数列的计算问题,应充分发挥项的“下标”的“指引”作用,以使运算简便.
规律方法总结
随堂即时巩固
课时活页训练
