【2012优化方案 精品课件】苏教版 数学 必修5:第一章本章优化总结
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第一章本章优化总结 |  | |
| 格式 | rar | ||
| 文件大小 | 576.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:35:06 | ||
图片预览








文档简介
(共26张PPT)
本章优化总结
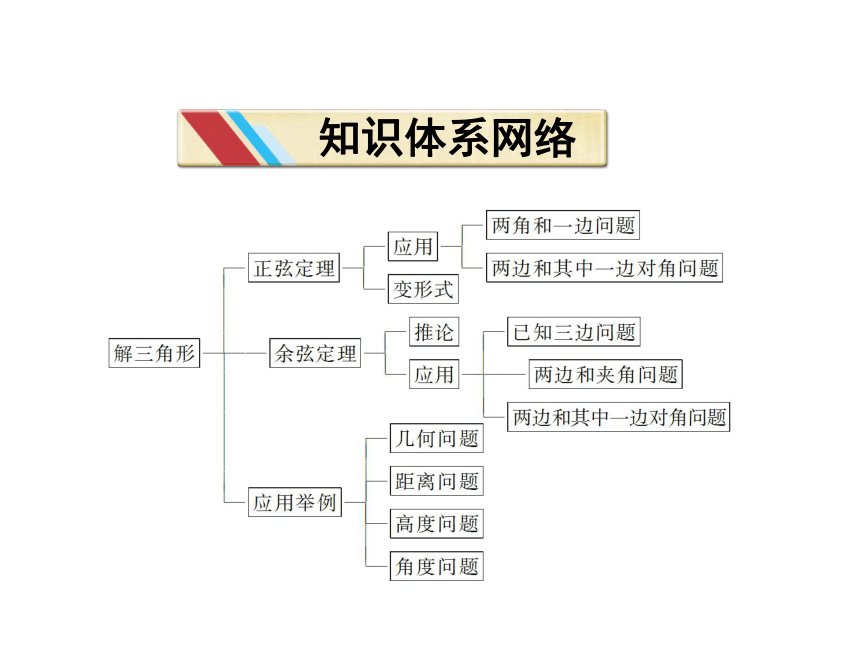
知识体系网络
专题探究精讲
专题一
直接利用正余弦定理求解三角形
值得注意的是已知三角形的任意两边与其中一边的对角,运用正弦定理解三角形时,解不确定,可结合三角形中大边对大角的性质去判断解的个数.
余弦定理有两方面的应用:一是已知三角形的两边和它们的夹角,求第三边和其他两角;二是已知三角形的三边,求三个角.在初中已经学过的勾股定理,它是余弦定理的特例,而余弦定理又可看做是勾股定理的推广,应用中要注意,定理的变式要能够灵活应用.
例1
【分析】 已知两边及其中一边的对角,用正、余弦定理均能解题.
专题二
三角形形状的判定
例2
【分析】 转化为角或边之间的关系,进而判断.
专题三
正、余弦定理的综合应用
例3
【分析】 由已知条件直接应用余弦定理与正弦定理.
专题四
解三角形在实际问题中的应用
某人在塔的正东沿着南偏西60°的方向前进40米以后,望见塔在东北方向,若沿途测得塔的最大仰角为30°,求塔高.
【分析】 构造出三角形,用正、余弦定理和三角形的相关知识求解.
例4
章末综合检测
两角和一边问题
应用
正弦定理
两边和其中一边对角问题
变形式
推论「已知三边问题
解三角形
余弦定理
应用
两边和夹角问题
两边和其中一边对角问题
几何问题
距离问题
应用举例
高度问题
角度问题
击链接
本章优化总结
知识体系网络
专题探究精讲
专题一
直接利用正余弦定理求解三角形
值得注意的是已知三角形的任意两边与其中一边的对角,运用正弦定理解三角形时,解不确定,可结合三角形中大边对大角的性质去判断解的个数.
余弦定理有两方面的应用:一是已知三角形的两边和它们的夹角,求第三边和其他两角;二是已知三角形的三边,求三个角.在初中已经学过的勾股定理,它是余弦定理的特例,而余弦定理又可看做是勾股定理的推广,应用中要注意,定理的变式要能够灵活应用.
例1
【分析】 已知两边及其中一边的对角,用正、余弦定理均能解题.
专题二
三角形形状的判定
例2
【分析】 转化为角或边之间的关系,进而判断.
专题三
正、余弦定理的综合应用
例3
【分析】 由已知条件直接应用余弦定理与正弦定理.
专题四
解三角形在实际问题中的应用
某人在塔的正东沿着南偏西60°的方向前进40米以后,望见塔在东北方向,若沿途测得塔的最大仰角为30°,求塔高.
【分析】 构造出三角形,用正、余弦定理和三角形的相关知识求解.
例4
章末综合检测
两角和一边问题
应用
正弦定理
两边和其中一边对角问题
变形式
推论「已知三边问题
解三角形
余弦定理
应用
两边和夹角问题
两边和其中一边对角问题
几何问题
距离问题
应用举例
高度问题
角度问题
击链接
