【2012优化方案 精品课件】苏教版 数学 必修5:第三章3.3.2
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第三章3.3.2 |  | |
| 格式 | rar | ||
| 文件大小 | 562.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 19:35:06 | ||
图片预览










文档简介
(共32张PPT)
3.3 二元一次不等式组与简单的线性规划问题
3.3.2 二元一次不等式组表示的平面区域
课标要求:1.体验并学会从实际问题的不等关系中抽象出二元一次不等式或二元一次不等式组的过程和方法.
2.会用直角坐标系中的平面区域表示二元一次不等式组的解集.
课标定位
重点难点:本节重点:1.理解二元一次不等式组表示的平面区域,能准确地画出这个平面区域.
2.能根据平面区域写出相应的二元一次不等式组.
本节难点:正确地理解二元一次不等式组表示的平面区域的意义和对“数形结合”思想的理解及应用.
基础知识梳理
1.二元一次不等式组
(1)由________________组成的不等式组,称为二元一次不等式组.
(2)满足二元一次不等式组的x和y的取值,构成有序实数对_______,所有这样的有序实数对_______构成的集合称为二元一次不等式组的解集.
2.判断二元一次不等式组表示的平面区域
(1)不等式组表示的区域是各个不等式表示的区域的公共部分.
(2)三个或三个以上不等式构成的不等式组画平面区域时,可先画出两个不等式的公共区域,再与第三个找公共区域,依次类推找下去,即可画出不等式组的平面区域.
二元一次不等式
(x,y)
(x,y)
课堂互动讲练
题型一
画出二元一次不等式组表示的平面区域
在画二元一次不等式组表示的平面区域时,应先画出每个不等式表示的区域,再取它们的公共部分即可,其步骤为:①画线;②定侧;③求“交”;④表示.
例1
【分析】 解答本题可先分别画出三个不等式所表示的平面区域,再找它们的公共部分.
【解】 如图所示.不等式x-y+5≥0
表示直线x-y+5=0上及右下方的点的
集合,不等式x+y+1>0表示直线
x+y+1=0右上方的点的集合
(不含边界),不等式x≤3表示直线x=3上及左方的点的集合,所以不等式组表示上述平面区域的公共部分(阴影部分).
【点评】 注意含边界的画成实线,不含边界的画成虚线.
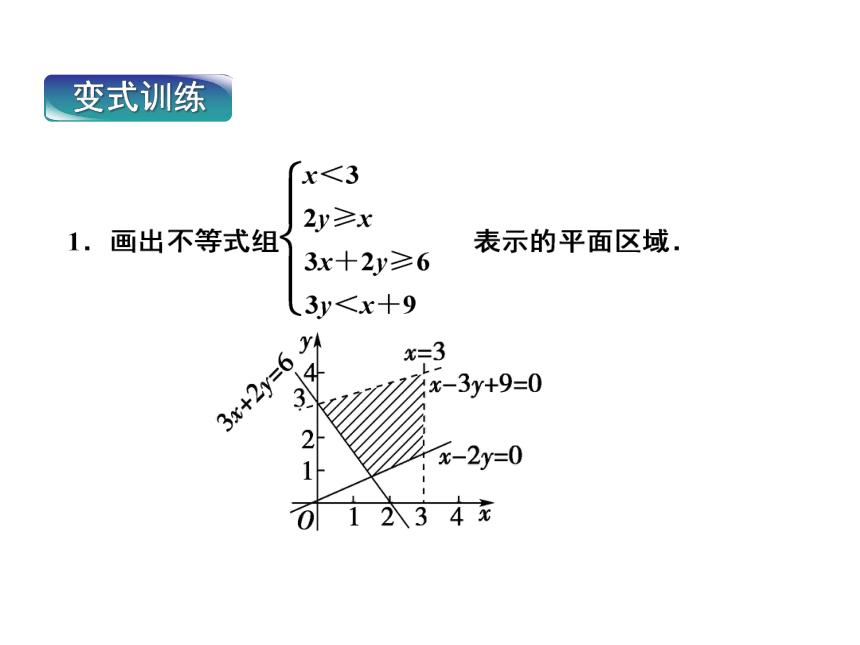
变式训练
解:不等式x<3表示直线x=3左侧的区域.
不等式2y≥x,即x-2y≤0表示直线x-2y=0上及左上方的区域.
不等式3x+2y≥6,即3x+2y-6≥0表示直线3x+2y-6=0上及右上方的区域.
不等式3y<x+9,即x-3y+9>0表示直线x-3y+9=0右下方的区域.
综上可得,不等式组表示的平面区域为如图所示的阴影部分.
题型二
由平面区域写不等式组
已知平面区域,用不等式(组)表示,其方法是:分别在所有直线外任取一点(如原点(0,0)),将其坐标代入Ax+By+C,判断正负即可.
例2
在△ABC中,A(3,-1)、B(-1,1)、C(1,3),写出△ABC区域所表示的二元一次不等式组.
【分析】 先求出直线AB、AC、BC的方程,然后根据区域写出不等式组.
【解】 由A(3,-1),C(1,3),得直线AC的方程为2x+y-5=0;由B(-1,1),C(1,3),得直线BC的方程为x-y+2=0;由A(3,-1),B(-1,1),得直线AB方程为x+2y-1=0.
【点评】 (1)根据区域写不等式组,要求交集与不等式组等价;(2)注意边界的虚实(是否有等号).
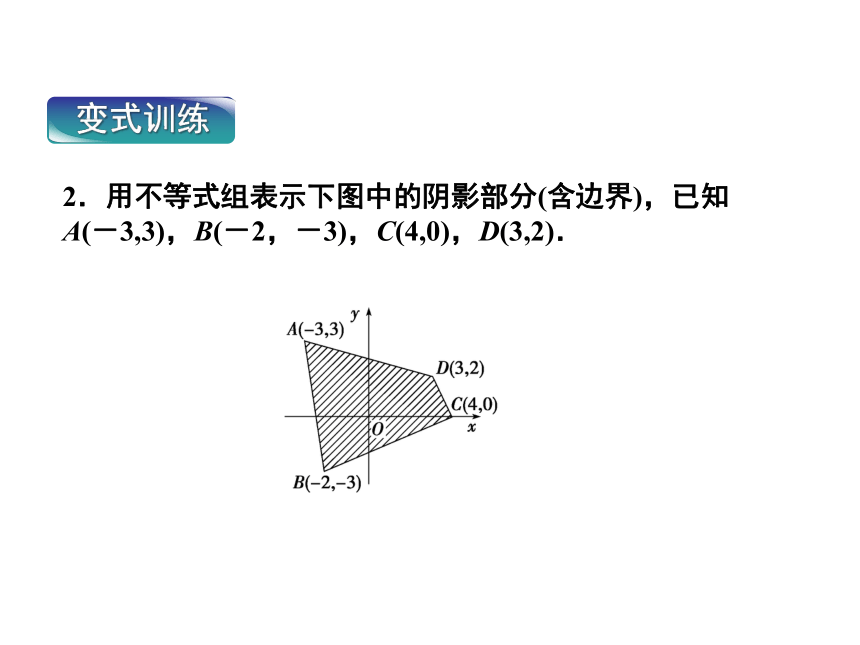
2.用不等式组表示下图中的阴影部分(含边界),已知A(-3,3),B(-2,-3),C(4,0),D(3,2).
变式训练
解:首先求出各条边所在的直线方程.
AB:6x+y+15=0;BC:x-2y-4=0;
CD:2x+y-8=0;DA:x+6y-15=0.
原点(0,0)在直线AB的右方,将(0,0)代入直线AB,得6·0+0+15>0,
所以,直线AB的右半平面区域为:6x+y+15≥0.
同理,直线BC的上半平面区域为:x-2y-4≤0,
直线CD的左半平面区域为:2x+y-8≤0,
直线DA的下半平面区域为:x+6y-15≤0.
题型三
不等式组表示的平面区域的面积
求平面区域的面积,先画出不等式组表示的平面区域,然后根据区域的形状求面积.若图形为规则的,则直接利用面积公式求解;若图形为不规则图形,可采取分割的方法,将平面区域分为几个规则图形后再求解.
例3
(2)求由不等式y≤2及|x|≤y≤|x|+1所表示的平面区域的面积.
【分析】 本题的两个小题的解题关键在于正确地描绘出边界直线,然后根据给出的不等式,判断出所表示的平面区域.
【解】 (1)如图①所示,其中的阴影部分便是不等式组表示的平面区域.
【点评】 本例(2)中也可先画出函数y=|x|和y=|x|+1的图象,再考虑围成的区域.
变式训练
3.在平面直角坐标系xOy中,已知平面区域A={(x,y)|x+y≤1,且x≥0,y≥0},则平面区域B={(x+y,x-y)|(x,y)∈A}的面积为________.
答案:1
题型四
求平面区域内的整数点
解决此类问题,应先画出平面区域,再在平面区域内找出整数解,常用的方法有:(1)打方格法;(2)代入比较法.
例4
【分析】 画出平面区域,观察区域内点的横、纵坐标的变化.
【解】 画出直线y-2x=0(画成实线),不等式y-2x≤0表示直线y-2x=0上及右下方的平面区域;
画出直线x+2y+3=0(画成虚线),不等式x+2y+3>0表示直线x+2y+3=0右上方的平面区域;
画出直线5x+3y-5=0(画成虚线),不等式5x+3y-5<0表示直线5x+3y-5=0左下方的平面区域 ;
显然,满足条件的平面区域中的整点为(1,-1),(2,-2),(0,0),(0,1)共有4个整点.
【点评】 平面区域中的整点问题,在解决时,常常先画平面区域,然后再找整点.
变式训练
4.在平面直角坐标系中,满足不等式(|x|-1)2+(|y|-1)2<2的整点(x,y)的个数是________.
解析:不等式(|x|-1)2+(|y|-1)2<2表示的平面区域分别关于x轴、y轴对称,也关于原点对称.因此可以先求(x-1)2+(y-1)2<2所对应的区域中的整点,共有5个点分别为(1,0)、(0,1)、(1,1)、(2,1)、(1,2),关于x轴对称的点有4个(0,-1)、(1,-1)、(2,-1)、(1,-2);关于y轴对称的点有4个(-1,0)、(-1,1)、(-2,1)、(-1,2);关于原点对称的点有3个(-1,-1)、(-2,-1)、(-1,-2),所以共有整点5+4+4+3=16(个).
答案:16
题型五
二元一次不等式组表示平面区域的实际应用
解答二元一次不等式(组)所表示的平面区域的应用问题时,建立恰当的数学模型,把实际问题转化为数学问题是关键,它所表示的平面区域是各个不等式所表示平面区域的公共部分.
例5
某工厂有甲、乙两种产品,计划每天产量都不少于15 t,已知生产甲产品1 t需煤9 t,电力4 kW·h,劳力3个;生产乙产品1 t需煤4 t,电力5 kW·h,劳力10个,但每天用煤不超过300 t,电力不超过200 kW·h,劳力只有300个,列出满足生产条件的数学关系式,并画出相应的平面区域.
【分析】 将题中数据列表如下:
产品
消耗量
资源 甲产品 乙产品 资源限额
煤(t) 9 4 300
电力(kW·h) 4 5 200
劳力(个) 3 10 300
【点评】 对于比较复杂的实际问题,通常借助于表格来分析.
变式训练
5.某公司从银行贷款不足250万元,分配给下属甲、乙两个工厂用以进行技术改造.已知甲厂可以从投入的金额中获取20%的利润;乙厂可以从投入的金额中获取25%的利润.若该公司计划从这笔贷款中至少获利60万元,请列出甲、乙两厂分配到的贷款金额所满足的数学关系式,并画出相应的平面区域.
规律方法总结
1.画二元一次不等式表示的平面区域常采用“直线定界,特殊点定域”的方法.特殊地,当C≠0时,常把原点作为此特殊点.
2.多以数形结合思想考虑问题.
随堂即时巩固
课时活页训练
3.3 二元一次不等式组与简单的线性规划问题
3.3.2 二元一次不等式组表示的平面区域
课标要求:1.体验并学会从实际问题的不等关系中抽象出二元一次不等式或二元一次不等式组的过程和方法.
2.会用直角坐标系中的平面区域表示二元一次不等式组的解集.
课标定位
重点难点:本节重点:1.理解二元一次不等式组表示的平面区域,能准确地画出这个平面区域.
2.能根据平面区域写出相应的二元一次不等式组.
本节难点:正确地理解二元一次不等式组表示的平面区域的意义和对“数形结合”思想的理解及应用.
基础知识梳理
1.二元一次不等式组
(1)由________________组成的不等式组,称为二元一次不等式组.
(2)满足二元一次不等式组的x和y的取值,构成有序实数对_______,所有这样的有序实数对_______构成的集合称为二元一次不等式组的解集.
2.判断二元一次不等式组表示的平面区域
(1)不等式组表示的区域是各个不等式表示的区域的公共部分.
(2)三个或三个以上不等式构成的不等式组画平面区域时,可先画出两个不等式的公共区域,再与第三个找公共区域,依次类推找下去,即可画出不等式组的平面区域.
二元一次不等式
(x,y)
(x,y)
课堂互动讲练
题型一
画出二元一次不等式组表示的平面区域
在画二元一次不等式组表示的平面区域时,应先画出每个不等式表示的区域,再取它们的公共部分即可,其步骤为:①画线;②定侧;③求“交”;④表示.
例1
【分析】 解答本题可先分别画出三个不等式所表示的平面区域,再找它们的公共部分.
【解】 如图所示.不等式x-y+5≥0
表示直线x-y+5=0上及右下方的点的
集合,不等式x+y+1>0表示直线
x+y+1=0右上方的点的集合
(不含边界),不等式x≤3表示直线x=3上及左方的点的集合,所以不等式组表示上述平面区域的公共部分(阴影部分).
【点评】 注意含边界的画成实线,不含边界的画成虚线.
变式训练
解:不等式x<3表示直线x=3左侧的区域.
不等式2y≥x,即x-2y≤0表示直线x-2y=0上及左上方的区域.
不等式3x+2y≥6,即3x+2y-6≥0表示直线3x+2y-6=0上及右上方的区域.
不等式3y<x+9,即x-3y+9>0表示直线x-3y+9=0右下方的区域.
综上可得,不等式组表示的平面区域为如图所示的阴影部分.
题型二
由平面区域写不等式组
已知平面区域,用不等式(组)表示,其方法是:分别在所有直线外任取一点(如原点(0,0)),将其坐标代入Ax+By+C,判断正负即可.
例2
在△ABC中,A(3,-1)、B(-1,1)、C(1,3),写出△ABC区域所表示的二元一次不等式组.
【分析】 先求出直线AB、AC、BC的方程,然后根据区域写出不等式组.
【解】 由A(3,-1),C(1,3),得直线AC的方程为2x+y-5=0;由B(-1,1),C(1,3),得直线BC的方程为x-y+2=0;由A(3,-1),B(-1,1),得直线AB方程为x+2y-1=0.
【点评】 (1)根据区域写不等式组,要求交集与不等式组等价;(2)注意边界的虚实(是否有等号).
2.用不等式组表示下图中的阴影部分(含边界),已知A(-3,3),B(-2,-3),C(4,0),D(3,2).
变式训练
解:首先求出各条边所在的直线方程.
AB:6x+y+15=0;BC:x-2y-4=0;
CD:2x+y-8=0;DA:x+6y-15=0.
原点(0,0)在直线AB的右方,将(0,0)代入直线AB,得6·0+0+15>0,
所以,直线AB的右半平面区域为:6x+y+15≥0.
同理,直线BC的上半平面区域为:x-2y-4≤0,
直线CD的左半平面区域为:2x+y-8≤0,
直线DA的下半平面区域为:x+6y-15≤0.
题型三
不等式组表示的平面区域的面积
求平面区域的面积,先画出不等式组表示的平面区域,然后根据区域的形状求面积.若图形为规则的,则直接利用面积公式求解;若图形为不规则图形,可采取分割的方法,将平面区域分为几个规则图形后再求解.
例3
(2)求由不等式y≤2及|x|≤y≤|x|+1所表示的平面区域的面积.
【分析】 本题的两个小题的解题关键在于正确地描绘出边界直线,然后根据给出的不等式,判断出所表示的平面区域.
【解】 (1)如图①所示,其中的阴影部分便是不等式组表示的平面区域.
【点评】 本例(2)中也可先画出函数y=|x|和y=|x|+1的图象,再考虑围成的区域.
变式训练
3.在平面直角坐标系xOy中,已知平面区域A={(x,y)|x+y≤1,且x≥0,y≥0},则平面区域B={(x+y,x-y)|(x,y)∈A}的面积为________.
答案:1
题型四
求平面区域内的整数点
解决此类问题,应先画出平面区域,再在平面区域内找出整数解,常用的方法有:(1)打方格法;(2)代入比较法.
例4
【分析】 画出平面区域,观察区域内点的横、纵坐标的变化.
【解】 画出直线y-2x=0(画成实线),不等式y-2x≤0表示直线y-2x=0上及右下方的平面区域;
画出直线x+2y+3=0(画成虚线),不等式x+2y+3>0表示直线x+2y+3=0右上方的平面区域;
画出直线5x+3y-5=0(画成虚线),不等式5x+3y-5<0表示直线5x+3y-5=0左下方的平面区域 ;
显然,满足条件的平面区域中的整点为(1,-1),(2,-2),(0,0),(0,1)共有4个整点.
【点评】 平面区域中的整点问题,在解决时,常常先画平面区域,然后再找整点.
变式训练
4.在平面直角坐标系中,满足不等式(|x|-1)2+(|y|-1)2<2的整点(x,y)的个数是________.
解析:不等式(|x|-1)2+(|y|-1)2<2表示的平面区域分别关于x轴、y轴对称,也关于原点对称.因此可以先求(x-1)2+(y-1)2<2所对应的区域中的整点,共有5个点分别为(1,0)、(0,1)、(1,1)、(2,1)、(1,2),关于x轴对称的点有4个(0,-1)、(1,-1)、(2,-1)、(1,-2);关于y轴对称的点有4个(-1,0)、(-1,1)、(-2,1)、(-1,2);关于原点对称的点有3个(-1,-1)、(-2,-1)、(-1,-2),所以共有整点5+4+4+3=16(个).
答案:16
题型五
二元一次不等式组表示平面区域的实际应用
解答二元一次不等式(组)所表示的平面区域的应用问题时,建立恰当的数学模型,把实际问题转化为数学问题是关键,它所表示的平面区域是各个不等式所表示平面区域的公共部分.
例5
某工厂有甲、乙两种产品,计划每天产量都不少于15 t,已知生产甲产品1 t需煤9 t,电力4 kW·h,劳力3个;生产乙产品1 t需煤4 t,电力5 kW·h,劳力10个,但每天用煤不超过300 t,电力不超过200 kW·h,劳力只有300个,列出满足生产条件的数学关系式,并画出相应的平面区域.
【分析】 将题中数据列表如下:
产品
消耗量
资源 甲产品 乙产品 资源限额
煤(t) 9 4 300
电力(kW·h) 4 5 200
劳力(个) 3 10 300
【点评】 对于比较复杂的实际问题,通常借助于表格来分析.
变式训练
5.某公司从银行贷款不足250万元,分配给下属甲、乙两个工厂用以进行技术改造.已知甲厂可以从投入的金额中获取20%的利润;乙厂可以从投入的金额中获取25%的利润.若该公司计划从这笔贷款中至少获利60万元,请列出甲、乙两厂分配到的贷款金额所满足的数学关系式,并画出相应的平面区域.
规律方法总结
1.画二元一次不等式表示的平面区域常采用“直线定界,特殊点定域”的方法.特殊地,当C≠0时,常把原点作为此特殊点.
2.多以数形结合思想考虑问题.
随堂即时巩固
课时活页训练
