【2012优化方案 精品课件】苏教版 数学 必修5:第三章本章优化总结
文档属性
| 名称 | 【2012优化方案 精品课件】苏教版 数学 必修5:第三章本章优化总结 |

|
|
| 格式 | rar | ||
| 文件大小 | 489.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-06 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
本章优化总结
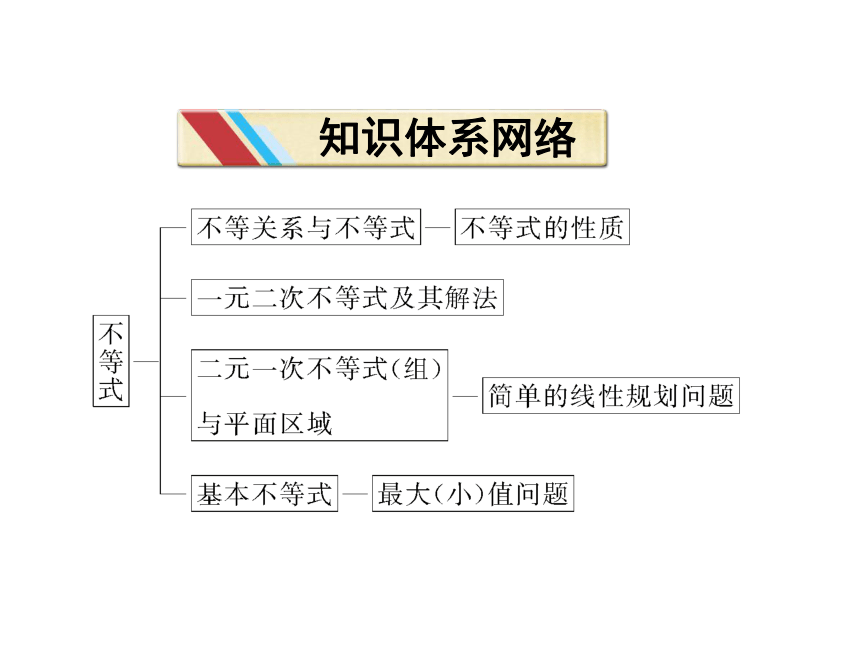
知识体系网络
专题探究精讲
专题一
不等式与函数、方程、数列的综合问题
1.利用不等式的性质、不等式的证明方法、解不等式等知识可以解决函数中的有关问题,主要体现在:利用不等式求函数的定义域、值域、最值、证明单调性等.
2.利用函数、方程、不等式之间的关系,可解决一元二次方程根的分布问题.
3.不等式与数列的综合题经常出现在高考压轴题中,主要体现在比较数列中两项的大小等.
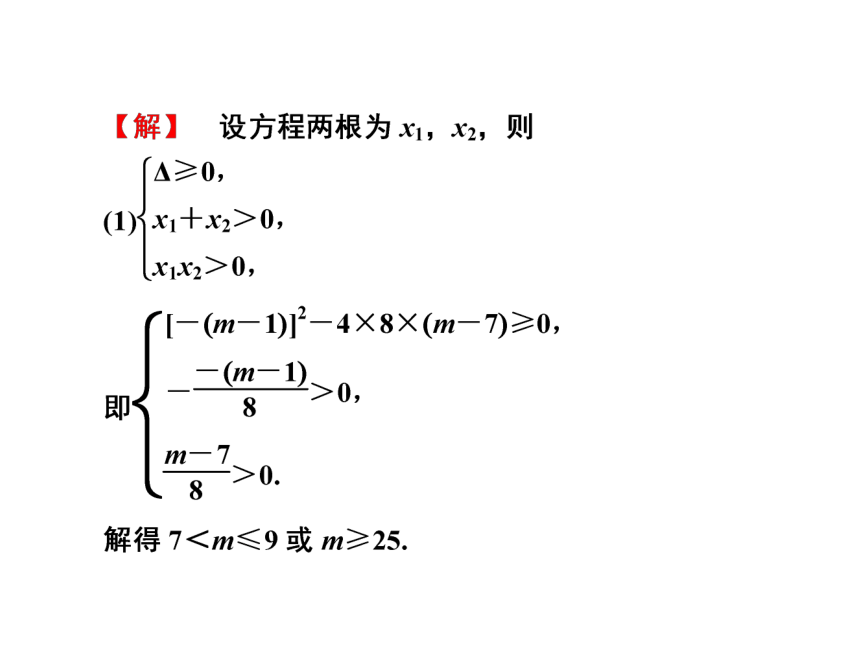
例1
m为何值时,关于x的方程8x2-(m-1)x+(m-7)=0的两根:(1)为正根;(2)为异号根且负根绝对值大于正根;(3)都大于1;(4)一根大于2,一根小于2.
【分析】 本题看似考查二次方程根的问题,细看是考查不等式问题,再分析可见是考查三个“二次”(即一元二次方程、一元二次不等式、二次函数)的问题,找出这一本质是解决本题的关键.
【点评】 三个“二次”之间的关系是实现它们之间相互转化的桥梁.联系三个“二次”的纽带是二次函数的图象,利用图象的形象直观可以准确把握三个“二次”之间的关系,牢固地记忆相关结论.同时,在分析、解决具体问题时,利用二次函数图象可以帮助我们迅速找到解题方法.
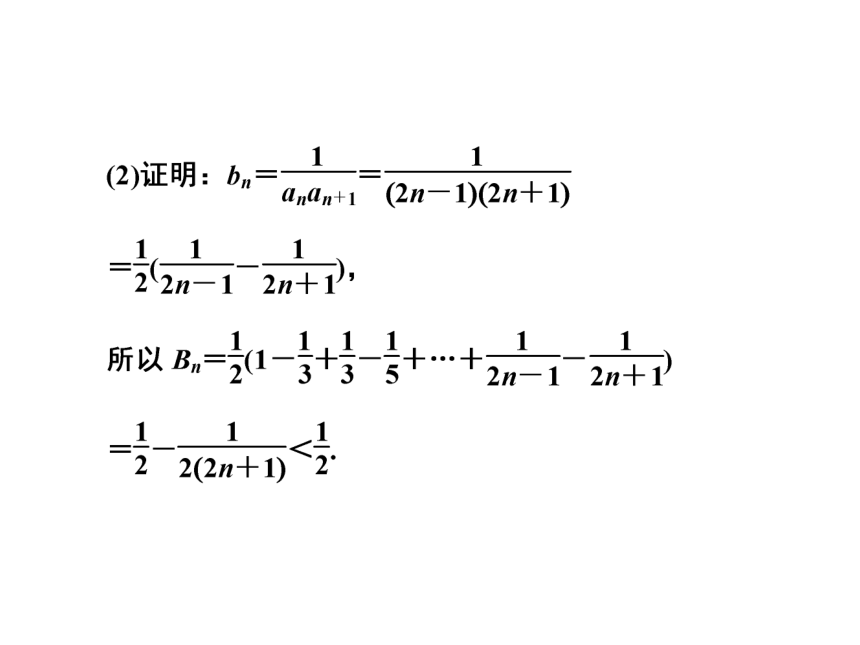
例2
【分析】 应先求和再放缩.
【点评】 如果数列的前n项和能直接求和或者通过变形后求和,则采用先求和再放缩的方法来证明不等式.求和的方式一般要用到等差、等比数列前n项和公式,或者利用分组、裂项、倒序相加等方法.
专题二
不等式恒成立问题
对于不等式恒成立求参数范围问题的常见类型及解法有以下几种
1.变更主元法:
根据实际情况的需要确定合适的主元,一般知道取值范围的变量要看作主元.
2.分离参数法:
若f(a)<g(x)恒成立,则f(a)<g(x)min.
若f(a)>g(x)恒成立,则f(a)>g(x)max.
3.数形结合法:
利用不等式与函数的关系,将恒成立问题通过函数图象直观化.
例3
设f(x)=mx2-mx-6+m,
(1)若对于m∈[-2,2],f(x)<0恒成立,求实数x的取值范围.
(2)若对于x∈[1,3],f(x)<0恒成立,求实数m的取值范围.
【分析】 (1)知道m的范围,所以应用变更主元法;
(2)应用分离参数法.
专题三
解含参数的不等式
解含参数的不等式,解答过程中的不确定因素常需进行分类讨论,如一元二次不等式的二次项系数含参数时分系数等于0、不等于0两类讨论;不等式两边同乘以(或除以)一个数时,要讨论这个数的符号;一元二次不等式对应方程根的情况不定或有实根但大小不定时要讨论.
例4
解关于x的不等式ax2+ax-1<0.(*)
【分析】 当a≠0时,不等式(*)为二次不等式,解二次不等式的关键是看二次项系数及判别式的正负,抓住这两条也就自然找到了分类的关键点.
【点评】 解含参数的一元二次不等式的关键是确定相应方程的两个根的大小.参数的分界点常按以下方法确定:(1)令最高项的系数等于0;(2)令两个根相等;(3)令判别式等于0.找到分界点后,可结合二次函数的图象在每一部分的特点写出相应不等式的解集.
专题四
利用基本不等式求最值
例5
当0<x<4时,求y=x(8-2x)的最大值.
【分析】 由0<x<4得8-2x>0,利用基本不等式求最值,必须和为定值或积为定值,此题为两个式子的积的形式,但其和不是定值,注意到2x+(8-2x)=8为定值,故只需将y=x(8-2x)凑上一个系数即可.
【点评】 本题无法直接运用基本不等式求解,但凑上系数后即可得到和为定值,就可利用基本不等式求得最大值.
例6
专题五
线性规划问题
求目标函数在约束条件下的最优解,一般步骤为:一寻求约束条件和目标函数;二作出可行域;三在可行域内求目标函数的最优解.特别要注意目标函数z=ax+by+c在直线ax+by=0平移过程中变化的规律和与图中直线斜率的关系,现实生活中简单的线性规划应用题也是高考的热点.
例7
【分析】 (1)为线性目标函数,是常规题型;
(2)应转化为求可行域内的点与原点的距离的平方求解.
【解】 作出可行域,如图中的阴影部分(含边界).
(1)令z=4x-3y=0得直线l:4x-3y=0.由图形可知当直线l平移至顶点C、B时z分别取最小值、最大值.
(2)设u=x2+y2,则u就是点(x,y)与原点之间的距离的平方,由图可知,B点到原点的距离最大,而当(x,y)在原点时,距离最小,为0.
所以umax=(-1)2+(-6)2=37,umin=0.
【点评】 解决线性规划问题,要准确画出可行域,然后分析出目标函数是否是线性的.不是线性的一般可转化为求斜率、求最值等.
章末综合检测
本章优化总结
知识体系网络
专题探究精讲
专题一
不等式与函数、方程、数列的综合问题
1.利用不等式的性质、不等式的证明方法、解不等式等知识可以解决函数中的有关问题,主要体现在:利用不等式求函数的定义域、值域、最值、证明单调性等.
2.利用函数、方程、不等式之间的关系,可解决一元二次方程根的分布问题.
3.不等式与数列的综合题经常出现在高考压轴题中,主要体现在比较数列中两项的大小等.
例1
m为何值时,关于x的方程8x2-(m-1)x+(m-7)=0的两根:(1)为正根;(2)为异号根且负根绝对值大于正根;(3)都大于1;(4)一根大于2,一根小于2.
【分析】 本题看似考查二次方程根的问题,细看是考查不等式问题,再分析可见是考查三个“二次”(即一元二次方程、一元二次不等式、二次函数)的问题,找出这一本质是解决本题的关键.
【点评】 三个“二次”之间的关系是实现它们之间相互转化的桥梁.联系三个“二次”的纽带是二次函数的图象,利用图象的形象直观可以准确把握三个“二次”之间的关系,牢固地记忆相关结论.同时,在分析、解决具体问题时,利用二次函数图象可以帮助我们迅速找到解题方法.
例2
【分析】 应先求和再放缩.
【点评】 如果数列的前n项和能直接求和或者通过变形后求和,则采用先求和再放缩的方法来证明不等式.求和的方式一般要用到等差、等比数列前n项和公式,或者利用分组、裂项、倒序相加等方法.
专题二
不等式恒成立问题
对于不等式恒成立求参数范围问题的常见类型及解法有以下几种
1.变更主元法:
根据实际情况的需要确定合适的主元,一般知道取值范围的变量要看作主元.
2.分离参数法:
若f(a)<g(x)恒成立,则f(a)<g(x)min.
若f(a)>g(x)恒成立,则f(a)>g(x)max.
3.数形结合法:
利用不等式与函数的关系,将恒成立问题通过函数图象直观化.
例3
设f(x)=mx2-mx-6+m,
(1)若对于m∈[-2,2],f(x)<0恒成立,求实数x的取值范围.
(2)若对于x∈[1,3],f(x)<0恒成立,求实数m的取值范围.
【分析】 (1)知道m的范围,所以应用变更主元法;
(2)应用分离参数法.
专题三
解含参数的不等式
解含参数的不等式,解答过程中的不确定因素常需进行分类讨论,如一元二次不等式的二次项系数含参数时分系数等于0、不等于0两类讨论;不等式两边同乘以(或除以)一个数时,要讨论这个数的符号;一元二次不等式对应方程根的情况不定或有实根但大小不定时要讨论.
例4
解关于x的不等式ax2+ax-1<0.(*)
【分析】 当a≠0时,不等式(*)为二次不等式,解二次不等式的关键是看二次项系数及判别式的正负,抓住这两条也就自然找到了分类的关键点.
【点评】 解含参数的一元二次不等式的关键是确定相应方程的两个根的大小.参数的分界点常按以下方法确定:(1)令最高项的系数等于0;(2)令两个根相等;(3)令判别式等于0.找到分界点后,可结合二次函数的图象在每一部分的特点写出相应不等式的解集.
专题四
利用基本不等式求最值
例5
当0<x<4时,求y=x(8-2x)的最大值.
【分析】 由0<x<4得8-2x>0,利用基本不等式求最值,必须和为定值或积为定值,此题为两个式子的积的形式,但其和不是定值,注意到2x+(8-2x)=8为定值,故只需将y=x(8-2x)凑上一个系数即可.
【点评】 本题无法直接运用基本不等式求解,但凑上系数后即可得到和为定值,就可利用基本不等式求得最大值.
例6
专题五
线性规划问题
求目标函数在约束条件下的最优解,一般步骤为:一寻求约束条件和目标函数;二作出可行域;三在可行域内求目标函数的最优解.特别要注意目标函数z=ax+by+c在直线ax+by=0平移过程中变化的规律和与图中直线斜率的关系,现实生活中简单的线性规划应用题也是高考的热点.
例7
【分析】 (1)为线性目标函数,是常规题型;
(2)应转化为求可行域内的点与原点的距离的平方求解.
【解】 作出可行域,如图中的阴影部分(含边界).
(1)令z=4x-3y=0得直线l:4x-3y=0.由图形可知当直线l平移至顶点C、B时z分别取最小值、最大值.
(2)设u=x2+y2,则u就是点(x,y)与原点之间的距离的平方,由图可知,B点到原点的距离最大,而当(x,y)在原点时,距离最小,为0.
所以umax=(-1)2+(-6)2=37,umin=0.
【点评】 解决线性规划问题,要准确画出可行域,然后分析出目标函数是否是线性的.不是线性的一般可转化为求斜率、求最值等.
章末综合检测
