人教版数学七年级上册3.3解一元一次方程(二)—去括号 课件(15张)
文档属性
| 名称 | 人教版数学七年级上册3.3解一元一次方程(二)—去括号 课件(15张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 21:20:16 | ||
图片预览




文档简介
(共15张PPT)
解一元一次方程(二)
——去括号
问题
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000kW·h(千瓦·时),全年用电15万kW·h.这个工厂去年上半年每月平均用电是多少?
新知引入
设上半年每月平均用电
x
kW·h,
则下半年每月平均用电
kW·h,
依题意有
6x+6(x-2000)=150000
(x-2000)
你会解这个方程吗?
化简下列各式:
(1)(-3a+2b)+3(a-b)
(2)-5a+4b-(-3a+b)
新知引入
解:(1)原式=-3a+2b+3a-3b=-b
(2)原式=-5a+4b+3a-b=-2a+3b
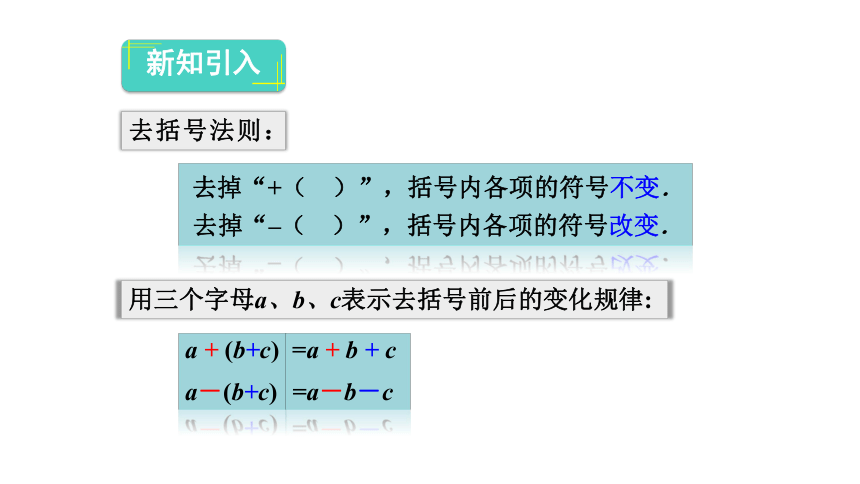
去括号法则:
去掉“+(
)”,括号内各项的符号不变.
去掉“–(
)”,括号内各项的符号改变.
用三个字母a、b、c表示去括号前后的变化规律:
a
+
(b+c)
a-(b+c)
=a
+
b
+
c
=a-b-c
新知引入
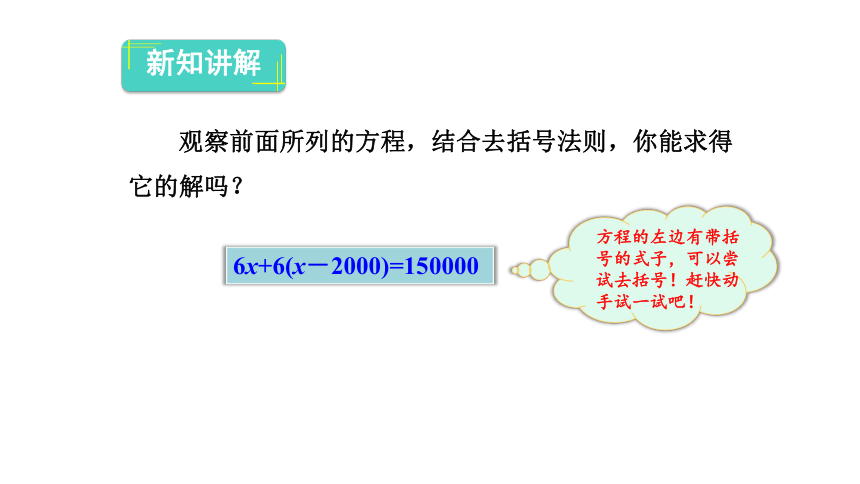
观察前面所列的方程,结合去括号法则,你能求得它的解吗?
新知讲解
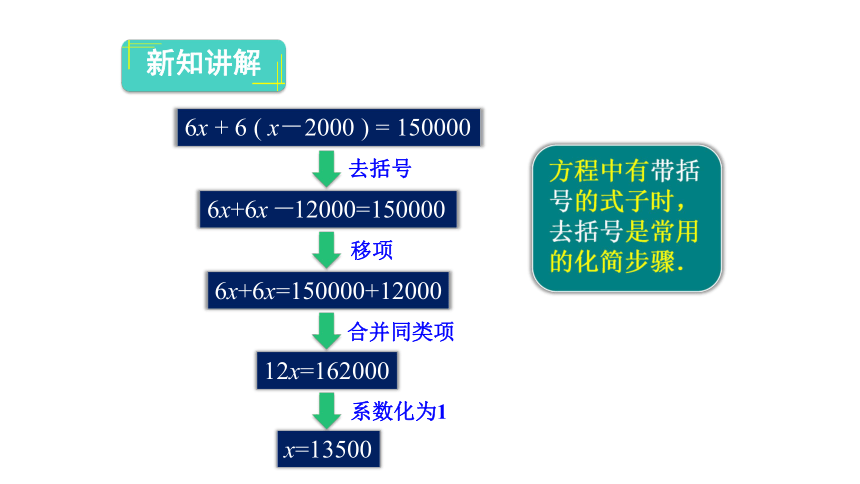
6x+6(x-2000)=150000
方程的左边有带括号的式子,可以尝试去括号!赶快动手试一试吧!
去括号
6x
+
6
(
x-2000
)
=
150000
6x+6x-12000=150000
6x+6x=150000+12000
12x=162000
x=13500
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
新知讲解
例1
解下列方程:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
新知应用
(1)2x-(x+10)=5x+2(x-1)
2x-x-10=5x+2x-2
2x-x-5x-2x=-2+10
-6x=8
?
新知应用
例1
解下列方程:
(2)3x-7(x-1)=3-2(x+3)
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
3x-7x+7=3-2x-6
3x-7x+2x=3-6-7
-2x=-10
x=5
通过以上解方程的过程,你能总结出解含有括号的一元一次方程的一般步骤吗?
新知应用
移
项
合并同类项
系数化为1
去括号
【分析】等量关系:这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
新知应用
例2
一艘船从甲码头到乙码头顺流而行,用了2
h;从乙码头返回甲码头逆流而行,用了2.5
h.已知水流的速度是
3
km/h,求船在静水中的平均速度.
【思考】题目中涉及到顺、逆流问题,这类问题中有哪些基本相等关系?
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
解:设船在静水中的平均速度为
x
km/h,则顺流速度
为(x+3)
km/h,逆流速度为(x-3)
km/h.
去括号,得
2x
+
6
=
2.5x-7.5
移项及合并同类项,得
0.5x
=
13.5
系数化为1,得
x
=
27
答:船在静水中的平均速度为
27
km/h.
根据顺流速度×顺流时间=逆流速度
×逆流时间
列出方程,得
2(x+3)
=
2.5(x-3)
新知应用
【提示】若一个月用电200度,则这个月应缴纳电费为
0.50×100+0.65×(200-100)=115元.
故当缴纳电费为310元时,该用户9月份用电量超过200度.
新知应用
例3
为鼓励居民节约用电,某地对居民用户用电收费标准作如下规定:每户每月用电如果不超过100度,那么每度按0.50元收费;如果超过100度不超过200度,那么超过部分每度按0.65元收费;如果超过200度,那么超过部分每度按0.75元收费.若某户居民在9月份缴纳电费310元,那么他这个月用电多少度?
答:他这个月用电460度.
解:设他这个月用电x度,根据题意,得
0.50×100+0.65×(200-100)+0.75(x-200)=310
解得x=460
方法总结:对于此类阶梯收费的题目,需要弄清楚各阶段的收费标准,以及各节点的费用;然后根据缴纳费用的金额,判断其处于哪个阶段,然后列方程求解即可.
新知应用
解一元一次方程
若括号外的因数是负数,去括号时,原括号内各项的符号要改变.
移
项
合并同类项
系数化为1
课堂总结
去括号
乘数与括号内多项式相乘时,乘数应乘括号内的每一项,不要漏乘.
谢谢聆听
解一元一次方程(二)
——去括号
问题
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000kW·h(千瓦·时),全年用电15万kW·h.这个工厂去年上半年每月平均用电是多少?
新知引入
设上半年每月平均用电
x
kW·h,
则下半年每月平均用电
kW·h,
依题意有
6x+6(x-2000)=150000
(x-2000)
你会解这个方程吗?
化简下列各式:
(1)(-3a+2b)+3(a-b)
(2)-5a+4b-(-3a+b)
新知引入
解:(1)原式=-3a+2b+3a-3b=-b
(2)原式=-5a+4b+3a-b=-2a+3b
去括号法则:
去掉“+(
)”,括号内各项的符号不变.
去掉“–(
)”,括号内各项的符号改变.
用三个字母a、b、c表示去括号前后的变化规律:
a
+
(b+c)
a-(b+c)
=a
+
b
+
c
=a-b-c
新知引入
观察前面所列的方程,结合去括号法则,你能求得它的解吗?
新知讲解
6x+6(x-2000)=150000
方程的左边有带括号的式子,可以尝试去括号!赶快动手试一试吧!
去括号
6x
+
6
(
x-2000
)
=
150000
6x+6x-12000=150000
6x+6x=150000+12000
12x=162000
x=13500
移项
合并同类项
系数化为1
方程中有带括号的式子时,去括号是常用的化简步骤.
新知讲解
例1
解下列方程:
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
新知应用
(1)2x-(x+10)=5x+2(x-1)
2x-x-10=5x+2x-2
2x-x-5x-2x=-2+10
-6x=8
?
新知应用
例1
解下列方程:
(2)3x-7(x-1)=3-2(x+3)
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
3x-7x+7=3-2x-6
3x-7x+2x=3-6-7
-2x=-10
x=5
通过以上解方程的过程,你能总结出解含有括号的一元一次方程的一般步骤吗?
新知应用
移
项
合并同类项
系数化为1
去括号
【分析】等量关系:这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
新知应用
例2
一艘船从甲码头到乙码头顺流而行,用了2
h;从乙码头返回甲码头逆流而行,用了2.5
h.已知水流的速度是
3
km/h,求船在静水中的平均速度.
【思考】题目中涉及到顺、逆流问题,这类问题中有哪些基本相等关系?
顺流速度=静水速度+水流速度
逆流速度=静水速度-水流速度
解:设船在静水中的平均速度为
x
km/h,则顺流速度
为(x+3)
km/h,逆流速度为(x-3)
km/h.
去括号,得
2x
+
6
=
2.5x-7.5
移项及合并同类项,得
0.5x
=
13.5
系数化为1,得
x
=
27
答:船在静水中的平均速度为
27
km/h.
根据顺流速度×顺流时间=逆流速度
×逆流时间
列出方程,得
2(x+3)
=
2.5(x-3)
新知应用
【提示】若一个月用电200度,则这个月应缴纳电费为
0.50×100+0.65×(200-100)=115元.
故当缴纳电费为310元时,该用户9月份用电量超过200度.
新知应用
例3
为鼓励居民节约用电,某地对居民用户用电收费标准作如下规定:每户每月用电如果不超过100度,那么每度按0.50元收费;如果超过100度不超过200度,那么超过部分每度按0.65元收费;如果超过200度,那么超过部分每度按0.75元收费.若某户居民在9月份缴纳电费310元,那么他这个月用电多少度?
答:他这个月用电460度.
解:设他这个月用电x度,根据题意,得
0.50×100+0.65×(200-100)+0.75(x-200)=310
解得x=460
方法总结:对于此类阶梯收费的题目,需要弄清楚各阶段的收费标准,以及各节点的费用;然后根据缴纳费用的金额,判断其处于哪个阶段,然后列方程求解即可.
新知应用
解一元一次方程
若括号外的因数是负数,去括号时,原括号内各项的符号要改变.
移
项
合并同类项
系数化为1
课堂总结
去括号
乘数与括号内多项式相乘时,乘数应乘括号内的每一项,不要漏乘.
谢谢聆听
