粤教版(2019)高中物理 必修第二册 第2章 第1节 匀速圆周运动学案
文档属性
| 名称 | 粤教版(2019)高中物理 必修第二册 第2章 第1节 匀速圆周运动学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 18:40:50 | ||
图片预览




文档简介
第一节 匀速圆周运动
学习目标:1.[物理观念]知道什么是圆周运动和匀速圆周运动。 2.[物理观念]会描述圆周运动的快慢,掌握线速度、角速度、周期的定义及它们之间的关系。 3.[科学思维]学会用比值定义法来描述物理量。会应用公式进行线速度、角速度、周期、频率、转速的计算。 4.[科学态度与责任]会分析常见的传动装置问题。
一、线速度和角速度
1.圆周运动:质点的运动轨迹是圆的运动。
2.匀速圆周运动:质点的线速度大小不随时间变化的圆周运动。
3.线速度
(1)定义:质点做匀速圆周运动时,质点通过的弧长l跟通过这段弧长所用时间t的比值。
(2)公式:v=。
(3)矢量性:线速度是矢量,其方向在圆周该点的切线方向上。
(4)单位:国际单位制中其单位是米每秒,符号是m/s。
(5)意义:表示匀速圆周运动的快慢。
4.角速度
(1)定义:质点做匀速圆周运动时,质点所在半径转过的角度θ跟所用时间t的比值。
(2)公式:ω=。
(3)单位:国际单位制中其单位是弧度每秒。符号是rad/s。
(4)意义:表示匀速圆周运动转动的快慢。
5.周期
(1)定义:匀速圆周运动的质点运动一周所用的时间,用符号T表示。
(2)单位:国际单位制中其单位是秒,符号s。
6.转速
(1)定义:物体转过的圈数与所用时间的比值,用符号n表示。
(2)单位:转速的单位是转每秒,符号是r/s,或者转每分,符号是r/min。
二、线速度、角速度、周期间的关系
1.线速度与周期的关系为v=。
2.角速度与周期的关系为ω=。
3.线速度与角速度的关系为v=ωr。
1.思考判断(正确的打“√”,错误的打“×”)
(1)匀速圆周运动是变速曲线运动。 (√)
(2)匀速圆周运动的线速度恒定不变。 (×)
(3)匀速圆周运动的角速度恒定不变。 (√)
(4)若匀速圆周运动的周期相同,则角速度大小及转速都相同。 (√)
2.(多选)关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是变速运动
C.匀速圆周运动是线速度不变的运动
D.匀速圆周运动是线速度大小不变的运动
BD [这里的“匀速”,不是“匀速度”,也不是“匀变速”,而是速率不变,匀速圆周运动实际上是一种速度大小不变、方向时刻改变的变速运动,故B、D正确。]
3.关于地球上不同位置的物体随地球自转的角速度关系、线速度大小关系,下列说法正确的是( )
A.处于同一纬度线上的海拔相同的物体线速度大小相等
B.处于同一经度线上的物体线速度大小相等
C.在赤道上的物体角速度最大
D.在两极处的物体线速度最大
A [地球上不同位置的物体随地球自转时,共轴转动,角速度相同,处于同一纬度线上的海拔相同的物体转动半径相等,由公式v=ωr分析知,线速度大小相等,故A正确,C错误;处于同一经度线上的物体转动半径不全相等,所以线速度不一定大小相等,故B错误;在两极处的物体转动半径最小,则线速度最小,故D错误。]
匀速圆周运动及描述的物理量
日常生活中,时钟指针的尖端、摩天轮上的座舱、电风扇工作时叶片上的点都在做圆周运动,它们的运动有何共同点?有什么不同之处?
提示:它们的运动都是圆周运动,共同点是运动轨迹都是圆周。不同点是转动的快慢不一样。
1.匀速圆周运动的特点
(1)匀速圆周运动一定是变速运动。因为速度是矢量,只要方向改变就说明速度发生了改变,而圆周运动的速度方向是时刻改变的,所以匀速圆周运动一定是变速曲线运动。
(2)匀速圆周运动是针对某个质点而言的,它在各个时刻的速度不同,因此质点必有加速度。
2.描述圆周运动的物理量之间的关系
【例1】 (多选)质点做匀速圆周运动,则( )
A.在任何相等的时间里,质点的位移都相等
B.在任何相等的时间里,质点通过的路程都相等
C.在任何相等的时间里,质点运动的平均速度都相同
D.在任何相等的时间里,连接质点和圆心的半径转过的角度都相等
思路点拨:(1)匀速圆周运动是变加速曲线运动。
(2)位移、平均速度是矢量。
BD [如图所示,由于线速度大小不变,根据线速度的定义,Δx=v·Δt,所以相等时间内通过的路程相等,B对;但位移sAB、sBC大小相等,方向并不相同,平均速度不同,A、C错;由角速度的定义ω=知Δt相同,Δθ=ωΔt相同,D对。]
1.线速度描述圆周运动质点通过弧长的快慢程度,匀速圆周运动线速度大小不变,方向不断变化。
2.角速度描述质点转过角度的快慢,匀速圆周运动的角速度恒定不变。
训练角度1 匀速圆周运动的理解
1.关于匀速圆周运动,下列说法正确的是( )
A.线速度的方向保持不变
B.线速度的大小保持不变
C.角速度不断变化
D.线速度和角速度都保持不变
B [做匀速圆周运动的物体,线速度大小不变,方向不断改变,故线速度不断变化,角速度保持不变,故选B。]
训练角度2 描述圆周运动物理量的计算
2.汽车在公路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长。某国产轿车的车轮半径约为30 cm,当该型号的轿车在高速公路上行驶时,驾驶员面前速率计的指针指在“120 km/h”上,可估算出该车轮的转速约为( )
A.1 000 r/s B.1 000 r/min
C.1 000 r/h D.2 000 r/s
B [由公式ω=2πn,得v=rω=2πrn,其中r=30 cm=0.3 m,v=120 km/h= m/s,代入得n= r/s,约为1 000 r/min。]
常见的传动方式
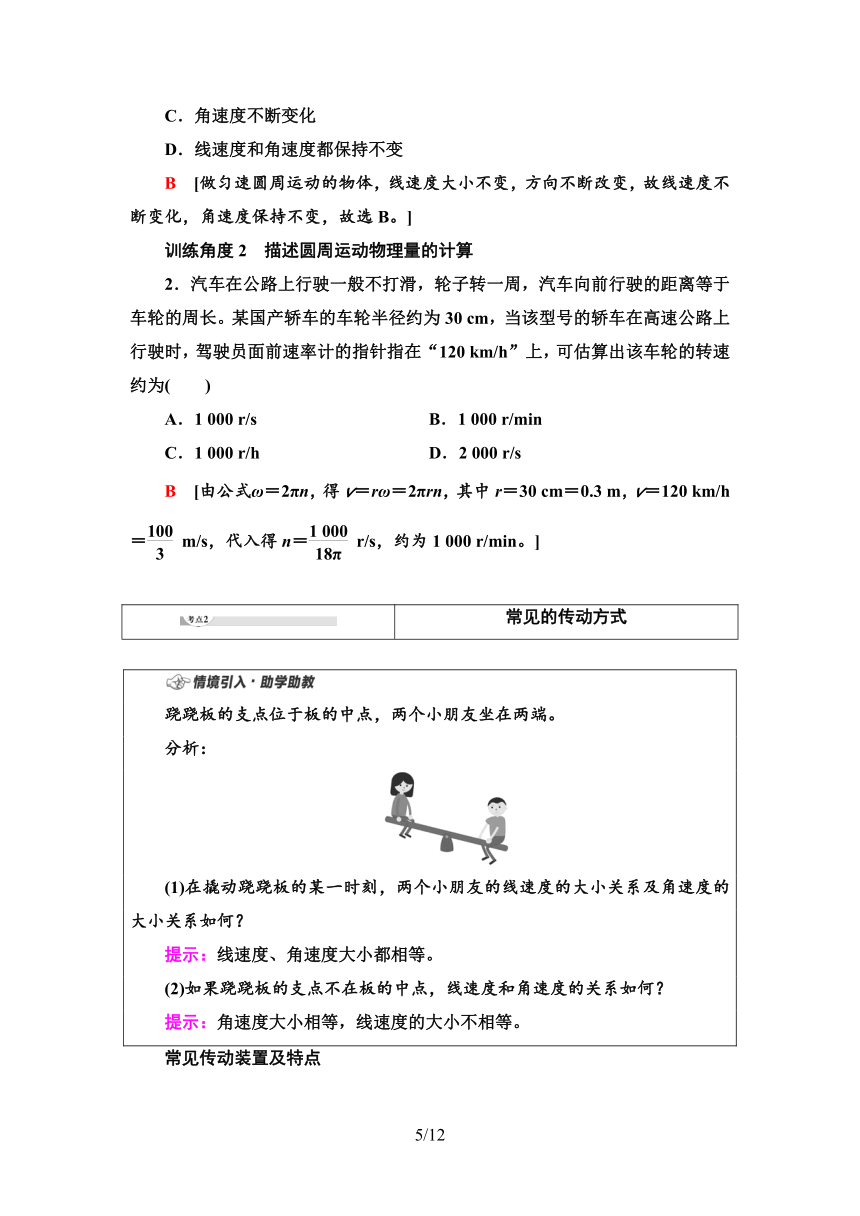
跷跷板的支点位于板的中点,两个小朋友坐在两端。
分析:
(1)在撬动跷跷板的某一时刻,两个小朋友的线速度的大小关系及角速度的大小关系如何?
提示:线速度、角速度大小都相等。
(2)如果跷跷板的支点不在板的中点,线速度和角速度的关系如何?
提示:角速度大小相等,线速度的大小不相等。
常见传动装置及特点
同轴传动 皮带传动 齿轮传动
装置 A、B两点在同轴的一个圆盘上
两个轮子用皮带连接,A、B两点分别是两个轮子边缘的点
两个齿轮轮齿啮合,A、B两点分别是两个齿轮边缘上的点
特点 角速度、周期相同 线速度相同 线速度相同
转动 方向 相同 相同 相反
规律 线速度与半径成正比:= 角速度与半径成反比:=。
周期与半径成正比:= 角速度与半径成反比:=。
周期与半径成正比:=
【例2】 如图所示,A、B、C分别是自行车的大齿轮、小齿轮和后轮的边缘上的三个点,到各自转动轴的距离分别为3r、r和10r。支起自行车后轮,在转动踏板的过程中,A、B、C三点( )
A.角速度大小关系是ωA>ωB=ωC
B.线速度大小关系是vA<vB<vC
C.转动周期之比TA∶TB∶TC=3∶1∶1
D.转速之比nA∶nB∶nC=3∶3∶1
思路点拨:抓住两个特点:(1)A、B两点的线速度大小相等。
(2)B、C两点的角速度相同。
C [大齿轮与小齿轮是链条传动,边缘点线速度相等,则有vA∶vB=1∶1,根据v=ωr,则有ωA∶ωB=rB∶rA=1∶3;小齿轮与后轮是同轴传动,角速度相等,则有ωB∶ωC=1∶1,根据v=ωr则有vB∶vC=1∶10,所以角速度大小关系是ωA∶ωB∶ωC=1∶3∶3,线速度大小关系是vA∶vB∶vC=1∶1∶10,根据T=可知TA∶TB∶TC=3∶1∶1,根据ω=2πn可知转速之比是nA∶nB∶nC=1∶3∶3,故选项C正确。]
三种传动装置的特征
3.科技馆的科普器材中常有如图所示的匀速率的传动装置:在大齿轮盘内嵌有三个等大的小齿轮。若齿轮的齿很小,大齿轮的半径(内径)是小齿轮半径的3倍,则当大齿轮顺时针匀速转动时,下列说法正确的是( )
A.小齿轮逆时针转动
B.小齿轮每个齿的线速度均相同
C.小齿轮的角速度是大齿轮角速度的3倍
D.小齿轮的线速度是大齿轮线速度的
C [大齿轮、小齿轮在转动过程中,两者的线速度大小相等,当大齿轮顺时针转动时,小齿轮也顺时针转动,故A、D错;
速度是矢量,具有方向,所以小齿轮每个齿的线速度不同,故B错;
由v=ωr知,当线速度大小相等时,角速度与半径成反比,故C对。]
圆周运动的周期性和多解问题
指尖陀螺是一种一个轴承对称结构、可以在手指上空转的小玩具,它是由一个双向或多向的对称体作为主体,在主体中间嵌入一个轴承的设计组合,整体构成一个可平面转动的新型物品,其中就包括可以悬浮在空中的指尖陀螺。
分析当指尖陀螺的转速达到一定程度时,我们看到好像陀螺处于静止状态一样,为什么?
提示:每经过特定的时间指尖陀螺就会转回到初始位置,所以我们看到好像陀螺不动一样。
1.问题特点
(1)研究对象:匀速圆周运动的多解问题含有两个做不同运动的物体。
(2)运动特点:一个物体做匀速圆周运动,另一个物体做其他形式的运动(如平抛运动,匀速直线运动等)。
(3)运动的关系:由于两物体运动的时间相等,根据等时性建立等式求解待求物理量。
2.分析技巧
(1)抓住联系点:明确题中两个物体的运动性质,抓住两个运动的联系点。
(2)先特殊后一般:先考虑第一个周期的情况,再根据运动的周期性,考虑多个周期时的规律。
【例3】 如图所示,半径为R的水平圆盘绕垂直于盘面的中心轴匀速转动,从正上方中心轴上距O点h处沿OB方向水平抛出一小球,要使小球与圆盘只碰一次,且落点为边缘的B点,求小球的初速度和圆盘转动的角速度ω。
思路点拨:突破的关键是:在小球下落的时间内圆盘转了几周。
[解析] 小球做平抛运动,在竖直方向上h=gt2,则运动时间t=。
又因为水平位移为R,
所以小球的初速度v==R。
在时间t内圆盘转过的角度
θ=N·2π,
又因为θ=ωt,所以圆盘转动的角速度
ω==2Nπ(N=1,2,3,…)。
[答案] R ω==2Nπ(N=1,2,3,…)
4.如图所示,直径为d的纸制圆筒,以角速度ω绕中心轴匀速转动,把枪口对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,忽略重力及空气阻力,则子弹速度不可能是( )
A. B.
C. D.
A [圆筒上只有一个弹孔,说明子弹从同一孔射入、射出,子弹运动的时间t=,圆筒转过的角度θ=2nπ+π(n=0,1,2,…),而ω=,联立可得v=(n=0,1,2,…),所以选项A不可能。]
1.物理观念:匀速圆周运动及线速度、角速度、周期等概念。
2.科学思维:描述圆周运动的物理量间的联系。
3.科学态度与责任:三种传动装置的分析。
1.关于做匀速圆周运动的物体,下列说法正确的是( )
A.因为在相等的时间内通过的圆弧长度相等,所以线速度恒定
B.如果物体在0.1 s内转过30°角,则角速度为300 rad/s
C.若半径r一定,则线速度与角速度成反比
D.若半径为r,周期为T,则线速度为v=
D [物体做匀速圆周运动时,线速度大小恒定,方向沿圆周的切线方向,在不断地改变,故选项A错误;角速度ω== rad/s= rad/s,选项B错误;线速度与角速度的关系为v=ωr,由该式可知,r一定时,v∝ω,选项C错误;由线速度的定义可得,在转动一周时有v=,选项D正确。]
2.(多选)如图所示,在风力发电机的叶片上有A、B、C三点,其中A、C在叶片的顶点,B在叶片的中点。当叶片转动时,这三点( )
A.线速度大小都相等
B.线速度方向都相同
C.角速度大小都相等
D.周期都相等
CD [首先A、B、C属于同轴传动,故它们的角速度、周期都相等,故C、D正确;由v=ωr知,它们的半径r不相等,故线速度的大小不相等,故A错误;A、B两点的线速度方向与C点的不同,线速度的方向沿着切线方向,故B错误。]
3.(多选)一精准转动的机械钟表,下列说法正确的是( )
A.秒针转动的周期最长
B.时针转动的转速最小
C.秒针转动的角速度最大
D.秒针的角速度为 rad/s
BCD [秒针转动的周期最短,角速度最大,A错误,C正确;时针转动的周期最长,转速最小,B正确;秒针的角速度为ω = rad/s= rad/s,故D正确。]
4.(多选)如图,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮半径的2倍,它们之间靠摩擦传动,接触面不打滑。下列说法正确的是( )
A.A与B线速度大小相等
B.B与C线速度大小相等
C.A的角速度是C的2倍
D.A与C角速度大小相等
AD [靠摩擦传动做匀速转动的大、小两轮接触面互不打滑,知A、B两点具有相同的线速度,故A项正确;点A和点C是同轴传动,角速度相等,C项错误,D项正确;点A和点B具有相同的线速度大小,又因为A、C具有相同的角速度,根据v=rω,可知B点的线速度大于C点的线速度,故B项错误。]
5.如图所示是一种粒子测量器,圆柱形容器的半径为R,容器壁上有一槽口A,其正对的位置是B,P是喷射高速粒子流的喷口,其喷射方向沿直径方向。现使容器以角速度ω匀速转动,则喷射的粒子流可以从槽口A进入容器,最后落在B′上,测得BB′的弧长为l,求喷射的粒子流的速度。
[解析] 粒子流沿直径方向做匀速直线运动的时间为t=,
在这段时间内,容器转过的弧长为k·2πR+l(k=0,1,2,…),
容器壁转动的线速度为ωR,因此有=(k=0,1,2,…),
解得v=(k=0,1,2,…)。
[答案] (k=0,1,2,…)
12/12
学习目标:1.[物理观念]知道什么是圆周运动和匀速圆周运动。 2.[物理观念]会描述圆周运动的快慢,掌握线速度、角速度、周期的定义及它们之间的关系。 3.[科学思维]学会用比值定义法来描述物理量。会应用公式进行线速度、角速度、周期、频率、转速的计算。 4.[科学态度与责任]会分析常见的传动装置问题。
一、线速度和角速度
1.圆周运动:质点的运动轨迹是圆的运动。
2.匀速圆周运动:质点的线速度大小不随时间变化的圆周运动。
3.线速度
(1)定义:质点做匀速圆周运动时,质点通过的弧长l跟通过这段弧长所用时间t的比值。
(2)公式:v=。
(3)矢量性:线速度是矢量,其方向在圆周该点的切线方向上。
(4)单位:国际单位制中其单位是米每秒,符号是m/s。
(5)意义:表示匀速圆周运动的快慢。
4.角速度
(1)定义:质点做匀速圆周运动时,质点所在半径转过的角度θ跟所用时间t的比值。
(2)公式:ω=。
(3)单位:国际单位制中其单位是弧度每秒。符号是rad/s。
(4)意义:表示匀速圆周运动转动的快慢。
5.周期
(1)定义:匀速圆周运动的质点运动一周所用的时间,用符号T表示。
(2)单位:国际单位制中其单位是秒,符号s。
6.转速
(1)定义:物体转过的圈数与所用时间的比值,用符号n表示。
(2)单位:转速的单位是转每秒,符号是r/s,或者转每分,符号是r/min。
二、线速度、角速度、周期间的关系
1.线速度与周期的关系为v=。
2.角速度与周期的关系为ω=。
3.线速度与角速度的关系为v=ωr。
1.思考判断(正确的打“√”,错误的打“×”)
(1)匀速圆周运动是变速曲线运动。 (√)
(2)匀速圆周运动的线速度恒定不变。 (×)
(3)匀速圆周运动的角速度恒定不变。 (√)
(4)若匀速圆周运动的周期相同,则角速度大小及转速都相同。 (√)
2.(多选)关于匀速圆周运动,下列说法正确的是( )
A.匀速圆周运动是匀速运动
B.匀速圆周运动是变速运动
C.匀速圆周运动是线速度不变的运动
D.匀速圆周运动是线速度大小不变的运动
BD [这里的“匀速”,不是“匀速度”,也不是“匀变速”,而是速率不变,匀速圆周运动实际上是一种速度大小不变、方向时刻改变的变速运动,故B、D正确。]
3.关于地球上不同位置的物体随地球自转的角速度关系、线速度大小关系,下列说法正确的是( )
A.处于同一纬度线上的海拔相同的物体线速度大小相等
B.处于同一经度线上的物体线速度大小相等
C.在赤道上的物体角速度最大
D.在两极处的物体线速度最大
A [地球上不同位置的物体随地球自转时,共轴转动,角速度相同,处于同一纬度线上的海拔相同的物体转动半径相等,由公式v=ωr分析知,线速度大小相等,故A正确,C错误;处于同一经度线上的物体转动半径不全相等,所以线速度不一定大小相等,故B错误;在两极处的物体转动半径最小,则线速度最小,故D错误。]
匀速圆周运动及描述的物理量
日常生活中,时钟指针的尖端、摩天轮上的座舱、电风扇工作时叶片上的点都在做圆周运动,它们的运动有何共同点?有什么不同之处?
提示:它们的运动都是圆周运动,共同点是运动轨迹都是圆周。不同点是转动的快慢不一样。
1.匀速圆周运动的特点
(1)匀速圆周运动一定是变速运动。因为速度是矢量,只要方向改变就说明速度发生了改变,而圆周运动的速度方向是时刻改变的,所以匀速圆周运动一定是变速曲线运动。
(2)匀速圆周运动是针对某个质点而言的,它在各个时刻的速度不同,因此质点必有加速度。
2.描述圆周运动的物理量之间的关系
【例1】 (多选)质点做匀速圆周运动,则( )
A.在任何相等的时间里,质点的位移都相等
B.在任何相等的时间里,质点通过的路程都相等
C.在任何相等的时间里,质点运动的平均速度都相同
D.在任何相等的时间里,连接质点和圆心的半径转过的角度都相等
思路点拨:(1)匀速圆周运动是变加速曲线运动。
(2)位移、平均速度是矢量。
BD [如图所示,由于线速度大小不变,根据线速度的定义,Δx=v·Δt,所以相等时间内通过的路程相等,B对;但位移sAB、sBC大小相等,方向并不相同,平均速度不同,A、C错;由角速度的定义ω=知Δt相同,Δθ=ωΔt相同,D对。]
1.线速度描述圆周运动质点通过弧长的快慢程度,匀速圆周运动线速度大小不变,方向不断变化。
2.角速度描述质点转过角度的快慢,匀速圆周运动的角速度恒定不变。
训练角度1 匀速圆周运动的理解
1.关于匀速圆周运动,下列说法正确的是( )
A.线速度的方向保持不变
B.线速度的大小保持不变
C.角速度不断变化
D.线速度和角速度都保持不变
B [做匀速圆周运动的物体,线速度大小不变,方向不断改变,故线速度不断变化,角速度保持不变,故选B。]
训练角度2 描述圆周运动物理量的计算
2.汽车在公路上行驶一般不打滑,轮子转一周,汽车向前行驶的距离等于车轮的周长。某国产轿车的车轮半径约为30 cm,当该型号的轿车在高速公路上行驶时,驾驶员面前速率计的指针指在“120 km/h”上,可估算出该车轮的转速约为( )
A.1 000 r/s B.1 000 r/min
C.1 000 r/h D.2 000 r/s
B [由公式ω=2πn,得v=rω=2πrn,其中r=30 cm=0.3 m,v=120 km/h= m/s,代入得n= r/s,约为1 000 r/min。]
常见的传动方式
跷跷板的支点位于板的中点,两个小朋友坐在两端。
分析:
(1)在撬动跷跷板的某一时刻,两个小朋友的线速度的大小关系及角速度的大小关系如何?
提示:线速度、角速度大小都相等。
(2)如果跷跷板的支点不在板的中点,线速度和角速度的关系如何?
提示:角速度大小相等,线速度的大小不相等。
常见传动装置及特点
同轴传动 皮带传动 齿轮传动
装置 A、B两点在同轴的一个圆盘上
两个轮子用皮带连接,A、B两点分别是两个轮子边缘的点
两个齿轮轮齿啮合,A、B两点分别是两个齿轮边缘上的点
特点 角速度、周期相同 线速度相同 线速度相同
转动 方向 相同 相同 相反
规律 线速度与半径成正比:= 角速度与半径成反比:=。
周期与半径成正比:= 角速度与半径成反比:=。
周期与半径成正比:=
【例2】 如图所示,A、B、C分别是自行车的大齿轮、小齿轮和后轮的边缘上的三个点,到各自转动轴的距离分别为3r、r和10r。支起自行车后轮,在转动踏板的过程中,A、B、C三点( )
A.角速度大小关系是ωA>ωB=ωC
B.线速度大小关系是vA<vB<vC
C.转动周期之比TA∶TB∶TC=3∶1∶1
D.转速之比nA∶nB∶nC=3∶3∶1
思路点拨:抓住两个特点:(1)A、B两点的线速度大小相等。
(2)B、C两点的角速度相同。
C [大齿轮与小齿轮是链条传动,边缘点线速度相等,则有vA∶vB=1∶1,根据v=ωr,则有ωA∶ωB=rB∶rA=1∶3;小齿轮与后轮是同轴传动,角速度相等,则有ωB∶ωC=1∶1,根据v=ωr则有vB∶vC=1∶10,所以角速度大小关系是ωA∶ωB∶ωC=1∶3∶3,线速度大小关系是vA∶vB∶vC=1∶1∶10,根据T=可知TA∶TB∶TC=3∶1∶1,根据ω=2πn可知转速之比是nA∶nB∶nC=1∶3∶3,故选项C正确。]
三种传动装置的特征
3.科技馆的科普器材中常有如图所示的匀速率的传动装置:在大齿轮盘内嵌有三个等大的小齿轮。若齿轮的齿很小,大齿轮的半径(内径)是小齿轮半径的3倍,则当大齿轮顺时针匀速转动时,下列说法正确的是( )
A.小齿轮逆时针转动
B.小齿轮每个齿的线速度均相同
C.小齿轮的角速度是大齿轮角速度的3倍
D.小齿轮的线速度是大齿轮线速度的
C [大齿轮、小齿轮在转动过程中,两者的线速度大小相等,当大齿轮顺时针转动时,小齿轮也顺时针转动,故A、D错;
速度是矢量,具有方向,所以小齿轮每个齿的线速度不同,故B错;
由v=ωr知,当线速度大小相等时,角速度与半径成反比,故C对。]
圆周运动的周期性和多解问题
指尖陀螺是一种一个轴承对称结构、可以在手指上空转的小玩具,它是由一个双向或多向的对称体作为主体,在主体中间嵌入一个轴承的设计组合,整体构成一个可平面转动的新型物品,其中就包括可以悬浮在空中的指尖陀螺。
分析当指尖陀螺的转速达到一定程度时,我们看到好像陀螺处于静止状态一样,为什么?
提示:每经过特定的时间指尖陀螺就会转回到初始位置,所以我们看到好像陀螺不动一样。
1.问题特点
(1)研究对象:匀速圆周运动的多解问题含有两个做不同运动的物体。
(2)运动特点:一个物体做匀速圆周运动,另一个物体做其他形式的运动(如平抛运动,匀速直线运动等)。
(3)运动的关系:由于两物体运动的时间相等,根据等时性建立等式求解待求物理量。
2.分析技巧
(1)抓住联系点:明确题中两个物体的运动性质,抓住两个运动的联系点。
(2)先特殊后一般:先考虑第一个周期的情况,再根据运动的周期性,考虑多个周期时的规律。
【例3】 如图所示,半径为R的水平圆盘绕垂直于盘面的中心轴匀速转动,从正上方中心轴上距O点h处沿OB方向水平抛出一小球,要使小球与圆盘只碰一次,且落点为边缘的B点,求小球的初速度和圆盘转动的角速度ω。
思路点拨:突破的关键是:在小球下落的时间内圆盘转了几周。
[解析] 小球做平抛运动,在竖直方向上h=gt2,则运动时间t=。
又因为水平位移为R,
所以小球的初速度v==R。
在时间t内圆盘转过的角度
θ=N·2π,
又因为θ=ωt,所以圆盘转动的角速度
ω==2Nπ(N=1,2,3,…)。
[答案] R ω==2Nπ(N=1,2,3,…)
4.如图所示,直径为d的纸制圆筒,以角速度ω绕中心轴匀速转动,把枪口对准圆筒轴线,使子弹穿过圆筒,结果发现圆筒上只有一个弹孔,忽略重力及空气阻力,则子弹速度不可能是( )
A. B.
C. D.
A [圆筒上只有一个弹孔,说明子弹从同一孔射入、射出,子弹运动的时间t=,圆筒转过的角度θ=2nπ+π(n=0,1,2,…),而ω=,联立可得v=(n=0,1,2,…),所以选项A不可能。]
1.物理观念:匀速圆周运动及线速度、角速度、周期等概念。
2.科学思维:描述圆周运动的物理量间的联系。
3.科学态度与责任:三种传动装置的分析。
1.关于做匀速圆周运动的物体,下列说法正确的是( )
A.因为在相等的时间内通过的圆弧长度相等,所以线速度恒定
B.如果物体在0.1 s内转过30°角,则角速度为300 rad/s
C.若半径r一定,则线速度与角速度成反比
D.若半径为r,周期为T,则线速度为v=
D [物体做匀速圆周运动时,线速度大小恒定,方向沿圆周的切线方向,在不断地改变,故选项A错误;角速度ω== rad/s= rad/s,选项B错误;线速度与角速度的关系为v=ωr,由该式可知,r一定时,v∝ω,选项C错误;由线速度的定义可得,在转动一周时有v=,选项D正确。]
2.(多选)如图所示,在风力发电机的叶片上有A、B、C三点,其中A、C在叶片的顶点,B在叶片的中点。当叶片转动时,这三点( )
A.线速度大小都相等
B.线速度方向都相同
C.角速度大小都相等
D.周期都相等
CD [首先A、B、C属于同轴传动,故它们的角速度、周期都相等,故C、D正确;由v=ωr知,它们的半径r不相等,故线速度的大小不相等,故A错误;A、B两点的线速度方向与C点的不同,线速度的方向沿着切线方向,故B错误。]
3.(多选)一精准转动的机械钟表,下列说法正确的是( )
A.秒针转动的周期最长
B.时针转动的转速最小
C.秒针转动的角速度最大
D.秒针的角速度为 rad/s
BCD [秒针转动的周期最短,角速度最大,A错误,C正确;时针转动的周期最长,转速最小,B正确;秒针的角速度为ω = rad/s= rad/s,故D正确。]
4.(多选)如图,A、B两点分别位于大、小轮的边缘上,C点位于大轮半径的中点,大轮的半径是小轮半径的2倍,它们之间靠摩擦传动,接触面不打滑。下列说法正确的是( )
A.A与B线速度大小相等
B.B与C线速度大小相等
C.A的角速度是C的2倍
D.A与C角速度大小相等
AD [靠摩擦传动做匀速转动的大、小两轮接触面互不打滑,知A、B两点具有相同的线速度,故A项正确;点A和点C是同轴传动,角速度相等,C项错误,D项正确;点A和点B具有相同的线速度大小,又因为A、C具有相同的角速度,根据v=rω,可知B点的线速度大于C点的线速度,故B项错误。]
5.如图所示是一种粒子测量器,圆柱形容器的半径为R,容器壁上有一槽口A,其正对的位置是B,P是喷射高速粒子流的喷口,其喷射方向沿直径方向。现使容器以角速度ω匀速转动,则喷射的粒子流可以从槽口A进入容器,最后落在B′上,测得BB′的弧长为l,求喷射的粒子流的速度。
[解析] 粒子流沿直径方向做匀速直线运动的时间为t=,
在这段时间内,容器转过的弧长为k·2πR+l(k=0,1,2,…),
容器壁转动的线速度为ωR,因此有=(k=0,1,2,…),
解得v=(k=0,1,2,…)。
[答案] (k=0,1,2,…)
12/12
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
