粤教版(2019)高中物理 必修第二册 第3章 第1节 认识天体运动学案
文档属性
| 名称 | 粤教版(2019)高中物理 必修第二册 第3章 第1节 认识天体运动学案 |  | |
| 格式 | doc | ||
| 文件大小 | 510.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 18:42:01 | ||
图片预览


文档简介
第一节 认识天体运动
学习目标:1.[物理观念]了解地心说和日心说。 2.[物理观念]理解开普勒定律。 3.[科学思维]能利用开普勒第三定律分析问题,理解公式=k中k的决定因素。
一、从地心说到日心说
1.地心说
地球是宇宙的中心,是静止不动的,太阳、月亮以及其他行星都绕地球运动。以古希腊科学家托勒密为代表人物。
2.日心说
太阳是宇宙的中心,地球和其他行星都围绕太阳运动。由波兰天文学家哥白尼提出。
二、开普勒定律
定律 内容 公式或图示
开普勒第一定律 所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上
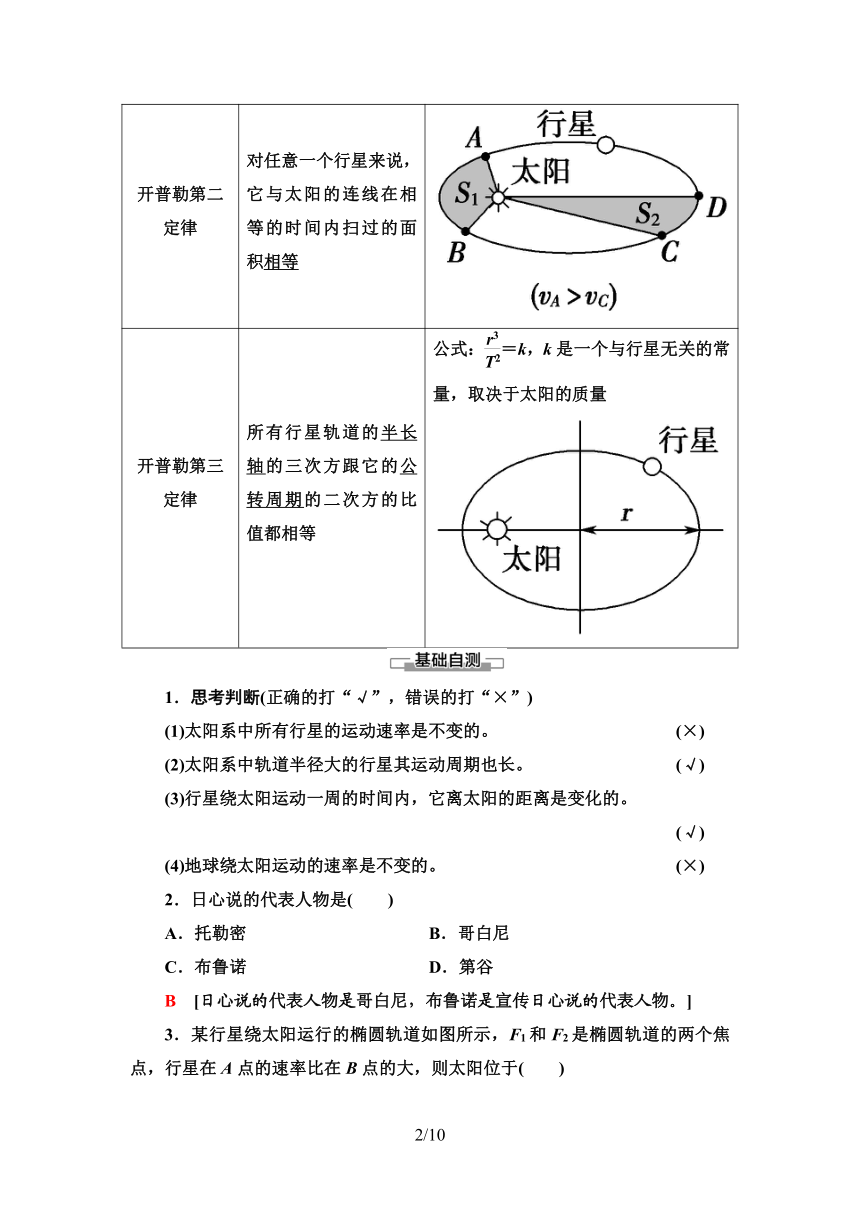
开普勒第二定律 对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等
开普勒第三定律 所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等 公式:=k,k是一个与行星无关的常量,取决于太阳的质量
1.思考判断(正确的打“√”,错误的打“×”)
(1)太阳系中所有行星的运动速率是不变的。 (×)
(2)太阳系中轨道半径大的行星其运动周期也长。 (√)
(3)行星绕太阳运动一周的时间内,它离太阳的距离是变化的。
(√)
(4)地球绕太阳运动的速率是不变的。 (×)
2.日心说的代表人物是( )
A.托勒密 B.哥白尼
C.布鲁诺 D.第谷
B [日心说的代表人物是哥白尼,布鲁诺是宣传日心说的代表人物。]
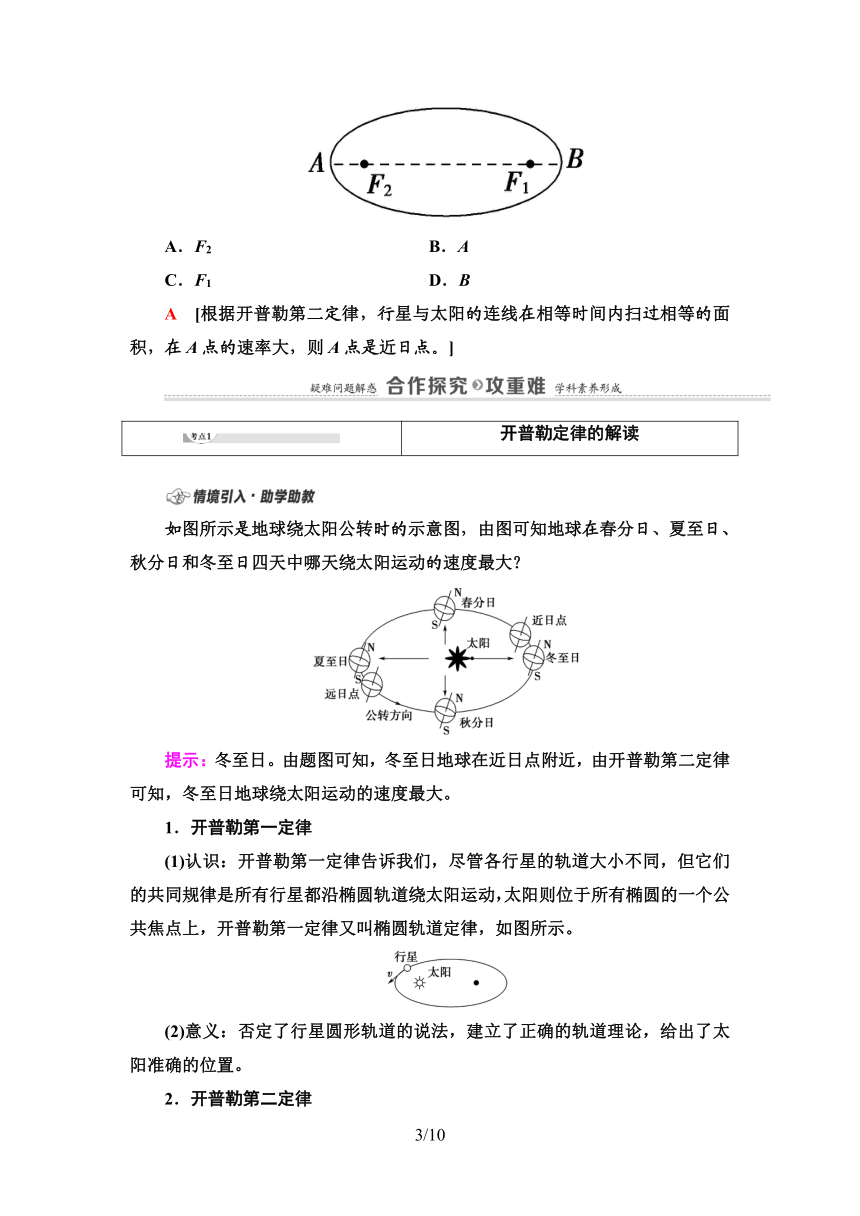
3.某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在A点的速率比在B点的大,则太阳位于( )
A.F2 B.A
C.F1 D.B
A [根据开普勒第二定律,行星与太阳的连线在相等时间内扫过相等的面积,在A点的速率大,则A点是近日点。]
开普勒定律的解读
如图所示是地球绕太阳公转时的示意图,由图可知地球在春分日、夏至日、秋分日和冬至日四天中哪天绕太阳运动的速度最大?
提示:冬至日。由题图可知,冬至日地球在近日点附近,由开普勒第二定律可知,冬至日地球绕太阳运动的速度最大。
1.开普勒第一定律
(1)认识:开普勒第一定律告诉我们,尽管各行星的轨道大小不同,但它们的共同规律是所有行星都沿椭圆轨道绕太阳运动,太阳则位于所有椭圆的一个公共焦点上,开普勒第一定律又叫椭圆轨道定律,如图所示。
(2)意义:否定了行星圆形轨道的说法,建立了正确的轨道理论,给出了太阳准确的位置。
2.开普勒第二定律
(1)认识:行星靠近太阳时速度增大,远离太阳时速度减小。近日点速度最大,远日点速度最小,又叫面积定律,如图所示。
(2)意义:描述了行星在其轨道上运行时,线速度的大小不断变化,并阐明了速度大小变化的数量关系。
3.开普勒第三定律
(1)认识:它揭示了周期与轨道半长轴之间的关系,椭圆轨道半长轴越长的行星,其公转周期越大;反之,其公转周期越小。因此又叫周期定律,如图所示。
(2)意义:比例常数k与行星无关,只与太阳有关,因此定律具有普遍性,即不同星系具有不同的常数,且常数是由中心天体决定的。
【例1】 (多选)如图所示,“嫦娥三号”绕月球沿椭圆轨道运行,绕行方向为逆时针方向,A、B分别为近月点和远月点,C是轨道上到A、B距离相等的点,则下列说法正确的是( )
A.“嫦娥三号”从A点到B点运行速率逐渐增大
B.“嫦娥三号”从A点到B点运行速率逐渐减小
C.“嫦娥三号”从A点到C点的运行时间等于四分之一周期
D.“嫦娥三号”从A点到C点的运行时间小于四分之一周期
BD [根据开普勒第二定律可知,“嫦娥三号”从A点到B点运行速率逐渐减小,选项A错误,B正确;“嫦娥三号”从A点到C点运行的平均速率大于从C点到B点运行的平均速率,可知从A点到C点运行时间小于四分之一周期,选项C错误,D正确。]
1.开普勒分别于1609年和1619年发表了他发现的行星运动规律,后人称之为开普勒行星运动定律。关于开普勒行星运动定律,下列说法正确的是( )
A.所有行星绕太阳运动的轨道都是圆,太阳处在圆心上
B.对任何一颗行星来说,离太阳越近,运行速率就越大
C.行星公转周期与行星的质量有关
D.所有行星的轨道的半长轴与公转周期成正比
B [根据开普勒第一定律:所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上,故A错误;根据开普勒第二定律:对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等,所以对任何一颗行星来说,离太阳越近,运行速率就越大,故B正确;开普勒第三定律中的公式=k,可知半长轴的三次方与公转周期的二次方成正比,式中的k只与中心天体的质量有关,与行星质量无关,故C、D错误。]
开普勒定律的计算应用
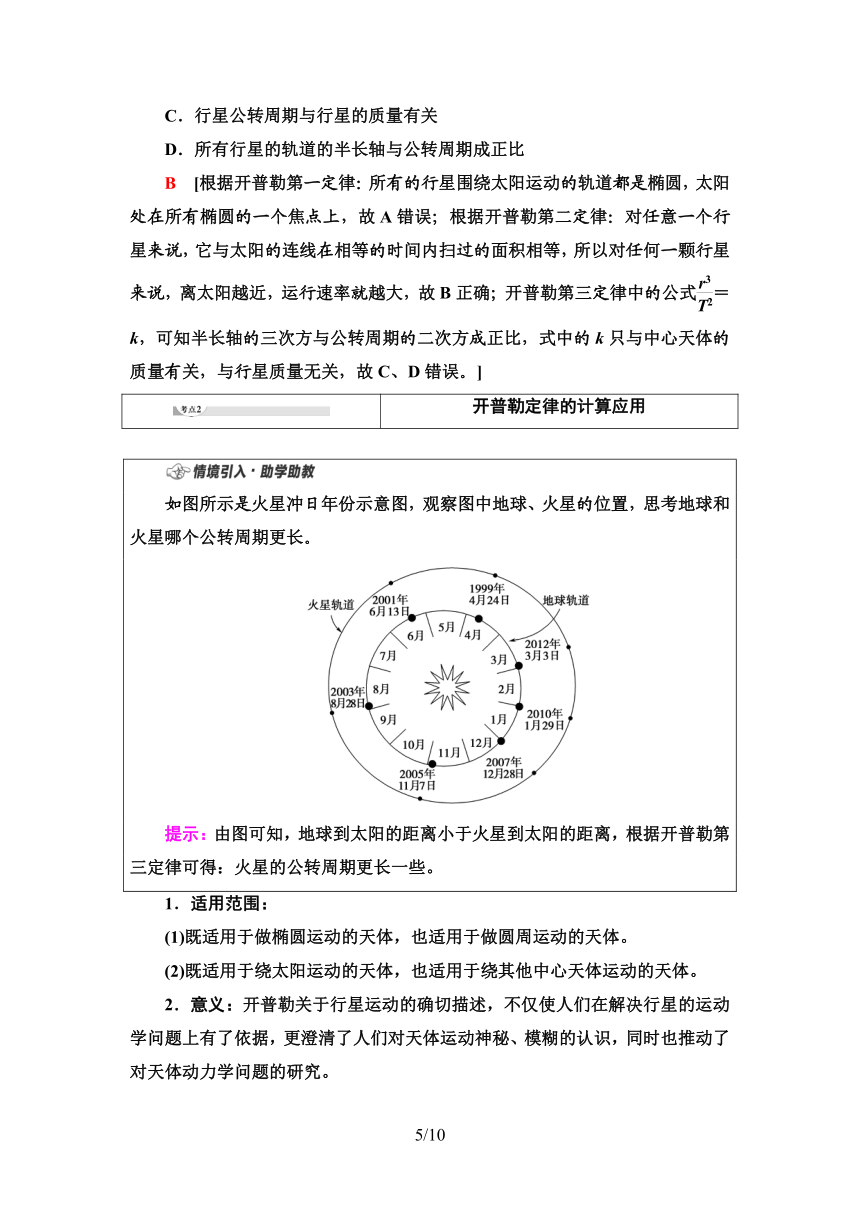
如图所示是火星冲日年份示意图,观察图中地球、火星的位置,思考地球和火星哪个公转周期更长。
提示:由图可知,地球到太阳的距离小于火星到太阳的距离,根据开普勒第三定律可得:火星的公转周期更长一些。
1.适用范围:
(1)既适用于做椭圆运动的天体,也适用于做圆周运动的天体。
(2)既适用于绕太阳运动的天体,也适用于绕其他中心天体运动的天体。
2.意义:开普勒关于行星运动的确切描述,不仅使人们在解决行星的运动学问题上有了依据,更澄清了人们对天体运动神秘、模糊的认识,同时也推动了对天体动力学问题的研究。
3.近似处理:由于行星的椭圆轨道都跟圆近似,在近似计算中,可以认为,行星都以太阳为圆心做匀速圆周运动。
【例2】 2015年12月29日,我国在西昌卫星发射中心用长征三号乙运载火箭成功发射“高分四号”卫星,卫星运行在地球静止轨道上。发射“高分四号”卫星时,先发射至近地圆轨道,然后再次点火,将卫星送入椭圆轨道,最后进入预定圆轨道。如图所示,地球的球心位于椭圆轨道的一个焦点上,A、B两点分别是“高分四号”卫星在椭圆轨道上的近地点和远地点。若已知B点距离地面高度为h,A点在地面附近(可认为A点到地心的距离为地球的半径R),且卫星所受阻力可以忽略不计,地球半径为R,在近地圆轨道上运行周期为T,求卫星从A点到B点的时间t。
思路点拨:(1)对圆轨道,半长轴等于圆的半径。
(2)卫星从A点到B点的时间为半个周期。
[解析] 当卫星做半径为R的圆周运动时,由开普勒第三定律k=
卫星从A点到B点做椭圆运动时,椭圆轨道半长轴r=R+
设卫星在椭圆轨道上运行时,周期为T′,则=
即,T′2)=
卫星从A点到B点的时间t=
得t=·。
[答案] 见解析
应用开普勒行星运动定律分析天体问题的方法
1.天体虽然做椭圆运动,有时为简化运算,可以把天体的运动当做圆周运动来研究,椭圆轨道的半长轴即圆轨道半径。
2.公式=k,对于同一中心天体的不同行星k的数值相同,对于不同的中心天体的行星k的数值不同。
3.比较行星轨道上不同点的速度大小,用开普勒第二定律;涉及椭圆轨道的周期问题,用开普勒第三定律。
训练角度1 开普勒第二定律
2.如图所示,某行星沿椭圆轨道运行,远日点到太阳的距离为a,近日点到太阳的距离为b,过远日点时行星的速率为va,过近日点时行星的速率为( )
A.vb=va B.vb=va
C.vb=va D.vb=va
C [若行星从轨道的A点经足够短的时间t运动到A′点,则与太阳的连线扫过的面积可看成扇形,其面积SA=;若行星从轨道的B点也经时间t运动到B′点,则与太阳的连线扫过的面积SB=;根据开普勒第二定律得=,即vb=va。]
训练角度2 开普勒第三定律
3.已知两个行星的质量关系为m1=2m2,公转周期关系为T1=2T2,则它们绕太阳运转轨道的半长轴之比为( )
A. B.2
C. D.
C [由开普勒第三定律知=k,其中比值k由中心天体决定,与行星的质量无关,可得=,则=)=)=。]
1.物理观念:(1)地心说和日心说。
(2)开普勒行星运动定律。
2.科学思维:利用开普勒定律分析天体运动问题。
3.科学态度与责任:了解人们探索太空的历史。
1.关于行星运动的规律,下列说法符合史实的是( )
A.开普勒在牛顿定律的基础上,导出了行星运动的规律
B.开普勒在天文观测数据的基础上,总结出了行星运动的规律
C.开普勒总结出了行星运动的规律,找出了行星按照这些规律运动的原因
D.开普勒总结出了行星运动的规律,发现了万有引力定律
B [开普勒在天文观测数据的基础上,总结出了开普勒三定律,找出了行星运动的规律,但并未找出行星按照这些规律运动的原因,是牛顿发现了万有引力定律。]
2.关于可能栖息生命的类地行星的运动,下列说法正确的是( )
A.所有行星都绕某一恒星做匀速圆周运动
B.所有行星都绕某一恒星做椭圆运动,且轨道都相同
C.离某一恒星越近的行星,其公转周期越小
D.离某一恒星越近的行星,其公转周期越大
C [根据开普勒三定律知,所有行星绕太阳的轨道都是椭圆,太阳位于椭圆的一个焦点上,但轨道不同,根据公式=k,半长轴越小,周期越小,把椭圆轨道近似看成圆轨道,即离某一恒星越近的行星,其公转周期越小。]
3.(多选)关于卫星绕地球的运动,根据开普勒定律,我们可以推出的正确结论有( )
A.人造地球卫星的轨道都是椭圆,地球在椭圆的一个焦点上
B.卫星绕地球运动的过程中,其速率与卫星到地心的距离有关,距离小时速率小
C.卫星离地球越远,周期越大
D.同一卫星绕不同的行星运动,的值都相同
AC [由开普勒第一定律知:所有地球卫星的轨道都是椭圆,且地球位于所有椭圆的公共焦点上,A正确;由开普勒第二定律知:卫星离地心的距离越小,速率越大,B项错误;由开普勒第三定律知:卫星离地球越远,周期越大,C正确;开普勒第三定律成立的条件是对同一行星的不同卫星,有=常量,对于绕不同行星运动的卫星,该常数不同,D错误。]
4.一人造卫星绕地球做匀速圆周运动,其轨道半径为月球绕地球轨道半径的,则此卫星运行的周期大约在( )
A.1~4天之间 B.4~8天之间
C.8~16天之间 D.16~20天之间
B [根据开普勒第三定律=k得=),即T卫=)T月,又因为T月约为27天,则T卫=×27天=天≈5.2天。]
5.近几年,全球兴起探索火星的热潮。发射火星探测器可按以下步骤进行,第一步,在地球表面用火箭对探测器进行加速,使之沿地球公转轨道运动。第二步是在适当时刻启用探测器上的火箭发动机,在短时间内对探测器沿原方向加速,使其速度值增加到适当值,从而使探测器沿着一个与地球轨道及火星轨道分别在长轴两端相切的半个椭圆轨道飞行,运行半个周期后正好飞行到火星表面附近,此时,启动探测器上的发动机,使之成为绕火星运转的卫星,然后采取措施使之降落在火星上,如图所示,设地球的轨道半径为R,火星的轨道半径为1.5R,探测器从地球运行轨道到火星运行轨道大约需要多长时间?
[解析] 由题可知,探测器在飞向火星的椭圆上运行时,其轨道半长轴为=1.25R
由开普勒第三定律可得
=
解得T′≈1.4T地
所以探测器从地球运行轨道到火星运行轨道所需时间t=≈0.7年。
[答案] 0.7年
10/10
学习目标:1.[物理观念]了解地心说和日心说。 2.[物理观念]理解开普勒定律。 3.[科学思维]能利用开普勒第三定律分析问题,理解公式=k中k的决定因素。
一、从地心说到日心说
1.地心说
地球是宇宙的中心,是静止不动的,太阳、月亮以及其他行星都绕地球运动。以古希腊科学家托勒密为代表人物。
2.日心说
太阳是宇宙的中心,地球和其他行星都围绕太阳运动。由波兰天文学家哥白尼提出。
二、开普勒定律
定律 内容 公式或图示
开普勒第一定律 所有行星绕太阳运动的轨道都是椭圆,太阳处在椭圆的一个焦点上
开普勒第二定律 对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等
开普勒第三定律 所有行星轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等 公式:=k,k是一个与行星无关的常量,取决于太阳的质量
1.思考判断(正确的打“√”,错误的打“×”)
(1)太阳系中所有行星的运动速率是不变的。 (×)
(2)太阳系中轨道半径大的行星其运动周期也长。 (√)
(3)行星绕太阳运动一周的时间内,它离太阳的距离是变化的。
(√)
(4)地球绕太阳运动的速率是不变的。 (×)
2.日心说的代表人物是( )
A.托勒密 B.哥白尼
C.布鲁诺 D.第谷
B [日心说的代表人物是哥白尼,布鲁诺是宣传日心说的代表人物。]
3.某行星绕太阳运行的椭圆轨道如图所示,F1和F2是椭圆轨道的两个焦点,行星在A点的速率比在B点的大,则太阳位于( )
A.F2 B.A
C.F1 D.B
A [根据开普勒第二定律,行星与太阳的连线在相等时间内扫过相等的面积,在A点的速率大,则A点是近日点。]
开普勒定律的解读
如图所示是地球绕太阳公转时的示意图,由图可知地球在春分日、夏至日、秋分日和冬至日四天中哪天绕太阳运动的速度最大?
提示:冬至日。由题图可知,冬至日地球在近日点附近,由开普勒第二定律可知,冬至日地球绕太阳运动的速度最大。
1.开普勒第一定律
(1)认识:开普勒第一定律告诉我们,尽管各行星的轨道大小不同,但它们的共同规律是所有行星都沿椭圆轨道绕太阳运动,太阳则位于所有椭圆的一个公共焦点上,开普勒第一定律又叫椭圆轨道定律,如图所示。
(2)意义:否定了行星圆形轨道的说法,建立了正确的轨道理论,给出了太阳准确的位置。
2.开普勒第二定律
(1)认识:行星靠近太阳时速度增大,远离太阳时速度减小。近日点速度最大,远日点速度最小,又叫面积定律,如图所示。
(2)意义:描述了行星在其轨道上运行时,线速度的大小不断变化,并阐明了速度大小变化的数量关系。
3.开普勒第三定律
(1)认识:它揭示了周期与轨道半长轴之间的关系,椭圆轨道半长轴越长的行星,其公转周期越大;反之,其公转周期越小。因此又叫周期定律,如图所示。
(2)意义:比例常数k与行星无关,只与太阳有关,因此定律具有普遍性,即不同星系具有不同的常数,且常数是由中心天体决定的。
【例1】 (多选)如图所示,“嫦娥三号”绕月球沿椭圆轨道运行,绕行方向为逆时针方向,A、B分别为近月点和远月点,C是轨道上到A、B距离相等的点,则下列说法正确的是( )
A.“嫦娥三号”从A点到B点运行速率逐渐增大
B.“嫦娥三号”从A点到B点运行速率逐渐减小
C.“嫦娥三号”从A点到C点的运行时间等于四分之一周期
D.“嫦娥三号”从A点到C点的运行时间小于四分之一周期
BD [根据开普勒第二定律可知,“嫦娥三号”从A点到B点运行速率逐渐减小,选项A错误,B正确;“嫦娥三号”从A点到C点运行的平均速率大于从C点到B点运行的平均速率,可知从A点到C点运行时间小于四分之一周期,选项C错误,D正确。]
1.开普勒分别于1609年和1619年发表了他发现的行星运动规律,后人称之为开普勒行星运动定律。关于开普勒行星运动定律,下列说法正确的是( )
A.所有行星绕太阳运动的轨道都是圆,太阳处在圆心上
B.对任何一颗行星来说,离太阳越近,运行速率就越大
C.行星公转周期与行星的质量有关
D.所有行星的轨道的半长轴与公转周期成正比
B [根据开普勒第一定律:所有的行星围绕太阳运动的轨道都是椭圆,太阳处在所有椭圆的一个焦点上,故A错误;根据开普勒第二定律:对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等,所以对任何一颗行星来说,离太阳越近,运行速率就越大,故B正确;开普勒第三定律中的公式=k,可知半长轴的三次方与公转周期的二次方成正比,式中的k只与中心天体的质量有关,与行星质量无关,故C、D错误。]
开普勒定律的计算应用
如图所示是火星冲日年份示意图,观察图中地球、火星的位置,思考地球和火星哪个公转周期更长。
提示:由图可知,地球到太阳的距离小于火星到太阳的距离,根据开普勒第三定律可得:火星的公转周期更长一些。
1.适用范围:
(1)既适用于做椭圆运动的天体,也适用于做圆周运动的天体。
(2)既适用于绕太阳运动的天体,也适用于绕其他中心天体运动的天体。
2.意义:开普勒关于行星运动的确切描述,不仅使人们在解决行星的运动学问题上有了依据,更澄清了人们对天体运动神秘、模糊的认识,同时也推动了对天体动力学问题的研究。
3.近似处理:由于行星的椭圆轨道都跟圆近似,在近似计算中,可以认为,行星都以太阳为圆心做匀速圆周运动。
【例2】 2015年12月29日,我国在西昌卫星发射中心用长征三号乙运载火箭成功发射“高分四号”卫星,卫星运行在地球静止轨道上。发射“高分四号”卫星时,先发射至近地圆轨道,然后再次点火,将卫星送入椭圆轨道,最后进入预定圆轨道。如图所示,地球的球心位于椭圆轨道的一个焦点上,A、B两点分别是“高分四号”卫星在椭圆轨道上的近地点和远地点。若已知B点距离地面高度为h,A点在地面附近(可认为A点到地心的距离为地球的半径R),且卫星所受阻力可以忽略不计,地球半径为R,在近地圆轨道上运行周期为T,求卫星从A点到B点的时间t。
思路点拨:(1)对圆轨道,半长轴等于圆的半径。
(2)卫星从A点到B点的时间为半个周期。
[解析] 当卫星做半径为R的圆周运动时,由开普勒第三定律k=
卫星从A点到B点做椭圆运动时,椭圆轨道半长轴r=R+
设卫星在椭圆轨道上运行时,周期为T′,则=
即,T′2)=
卫星从A点到B点的时间t=
得t=·。
[答案] 见解析
应用开普勒行星运动定律分析天体问题的方法
1.天体虽然做椭圆运动,有时为简化运算,可以把天体的运动当做圆周运动来研究,椭圆轨道的半长轴即圆轨道半径。
2.公式=k,对于同一中心天体的不同行星k的数值相同,对于不同的中心天体的行星k的数值不同。
3.比较行星轨道上不同点的速度大小,用开普勒第二定律;涉及椭圆轨道的周期问题,用开普勒第三定律。
训练角度1 开普勒第二定律
2.如图所示,某行星沿椭圆轨道运行,远日点到太阳的距离为a,近日点到太阳的距离为b,过远日点时行星的速率为va,过近日点时行星的速率为( )
A.vb=va B.vb=va
C.vb=va D.vb=va
C [若行星从轨道的A点经足够短的时间t运动到A′点,则与太阳的连线扫过的面积可看成扇形,其面积SA=;若行星从轨道的B点也经时间t运动到B′点,则与太阳的连线扫过的面积SB=;根据开普勒第二定律得=,即vb=va。]
训练角度2 开普勒第三定律
3.已知两个行星的质量关系为m1=2m2,公转周期关系为T1=2T2,则它们绕太阳运转轨道的半长轴之比为( )
A. B.2
C. D.
C [由开普勒第三定律知=k,其中比值k由中心天体决定,与行星的质量无关,可得=,则=)=)=。]
1.物理观念:(1)地心说和日心说。
(2)开普勒行星运动定律。
2.科学思维:利用开普勒定律分析天体运动问题。
3.科学态度与责任:了解人们探索太空的历史。
1.关于行星运动的规律,下列说法符合史实的是( )
A.开普勒在牛顿定律的基础上,导出了行星运动的规律
B.开普勒在天文观测数据的基础上,总结出了行星运动的规律
C.开普勒总结出了行星运动的规律,找出了行星按照这些规律运动的原因
D.开普勒总结出了行星运动的规律,发现了万有引力定律
B [开普勒在天文观测数据的基础上,总结出了开普勒三定律,找出了行星运动的规律,但并未找出行星按照这些规律运动的原因,是牛顿发现了万有引力定律。]
2.关于可能栖息生命的类地行星的运动,下列说法正确的是( )
A.所有行星都绕某一恒星做匀速圆周运动
B.所有行星都绕某一恒星做椭圆运动,且轨道都相同
C.离某一恒星越近的行星,其公转周期越小
D.离某一恒星越近的行星,其公转周期越大
C [根据开普勒三定律知,所有行星绕太阳的轨道都是椭圆,太阳位于椭圆的一个焦点上,但轨道不同,根据公式=k,半长轴越小,周期越小,把椭圆轨道近似看成圆轨道,即离某一恒星越近的行星,其公转周期越小。]
3.(多选)关于卫星绕地球的运动,根据开普勒定律,我们可以推出的正确结论有( )
A.人造地球卫星的轨道都是椭圆,地球在椭圆的一个焦点上
B.卫星绕地球运动的过程中,其速率与卫星到地心的距离有关,距离小时速率小
C.卫星离地球越远,周期越大
D.同一卫星绕不同的行星运动,的值都相同
AC [由开普勒第一定律知:所有地球卫星的轨道都是椭圆,且地球位于所有椭圆的公共焦点上,A正确;由开普勒第二定律知:卫星离地心的距离越小,速率越大,B项错误;由开普勒第三定律知:卫星离地球越远,周期越大,C正确;开普勒第三定律成立的条件是对同一行星的不同卫星,有=常量,对于绕不同行星运动的卫星,该常数不同,D错误。]
4.一人造卫星绕地球做匀速圆周运动,其轨道半径为月球绕地球轨道半径的,则此卫星运行的周期大约在( )
A.1~4天之间 B.4~8天之间
C.8~16天之间 D.16~20天之间
B [根据开普勒第三定律=k得=),即T卫=)T月,又因为T月约为27天,则T卫=×27天=天≈5.2天。]
5.近几年,全球兴起探索火星的热潮。发射火星探测器可按以下步骤进行,第一步,在地球表面用火箭对探测器进行加速,使之沿地球公转轨道运动。第二步是在适当时刻启用探测器上的火箭发动机,在短时间内对探测器沿原方向加速,使其速度值增加到适当值,从而使探测器沿着一个与地球轨道及火星轨道分别在长轴两端相切的半个椭圆轨道飞行,运行半个周期后正好飞行到火星表面附近,此时,启动探测器上的发动机,使之成为绕火星运转的卫星,然后采取措施使之降落在火星上,如图所示,设地球的轨道半径为R,火星的轨道半径为1.5R,探测器从地球运行轨道到火星运行轨道大约需要多长时间?
[解析] 由题可知,探测器在飞向火星的椭圆上运行时,其轨道半长轴为=1.25R
由开普勒第三定律可得
=
解得T′≈1.4T地
所以探测器从地球运行轨道到火星运行轨道所需时间t=≈0.7年。
[答案] 0.7年
10/10
同课章节目录
- 第一章 抛体运动
- 第一节 曲线运动
- 第二节 运动的合成与分解
- 第三节 平抛运动
- 第四节 生活和生产中的抛体运动
- 第二章 圆周运动
- 第一节 匀速圆周运动
- 第二节 向心力与向心加速度
- 第三节 生活中的圆周运动
- 第四节 离心现象及其应用
- 第三章 万有引力定律
- 第一节 认识天体运动
- 第二节 认识万有引力定律
- 第三节 万有引力定律的应用
- 第四节 宇宙速度与航天
- 第四章 机械能及其守恒定律
- 第一节 功
- 第二节 功率
- 第三节 动能 动能定理
- 第四节 势能
- 第五节 机械能守恒定律
- 第六节 验证机械能守恒定律
- 第七节 生产和生活中的机械能守恒
- 第五章 牛顿力学的局限性与相对论初步
- 第一节 牛顿力学的成就与局限性
- 第二节 相对论时空观
- 第三节 宇宙起源和演化
