粤教版(2019)高中物理 必修第三册 第5章 第1节 电路中的能量学案
文档属性
| 名称 | 粤教版(2019)高中物理 必修第三册 第5章 第1节 电路中的能量学案 |

|
|
| 格式 | doc | ||
| 文件大小 | 510.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 粤教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-20 20:38:17 | ||
图片预览




文档简介
第一节 电路中的能量
学习目标:1.[物理观念]理解电功、电功率的概念并能进行相关的计算。 2.[物理观念]知道焦耳定律,知道电功率与热功率的区别和联系。 3.[科学思维]知道纯电阻电路和非纯电阻电路的区别,会结合实际问题区分电功和电热。 4.[科学思维]理解闭合电路的各种功率及相关运算。
一、电功和电功率
1.电功
(1)定义:电流通过一段电路时,自由电荷在电场力的推动下做定向移动,电场力对自由电荷所做的功,称为电功。
(2)公式:W=UIt,单位:焦耳,符号:J。
2.电功率
(1)定义:电流做功与完成这些功所用时间之比叫做电功率。
(2)公式:P==UI,单位:瓦特,符号:W,1 kW=103 W。
二、焦耳定律
1.焦耳定律
(1)内容:电流通过导体产生的热量跟电流的二次方成正比,与导体的电阻及通电时间成正比。
(2)公式:Q=I2Rt。
2.热功率:一段电路因发热消耗的功率,P=I2R。
三、闭合电路中的能量
电源的功率 电源的输出功率 电源的内耗功率
公式 P=EI P出=U外I P内=U内I
意义 电源提供电能的功率 外电路消耗电能的功率 内电路消耗电能的功率
关系 P=P出+P内
1.正误判断(正确的打“√”,错误的打“×”)
(1)电流通过导体做的功越多,电功率越大。 (×)
(2)电炉、电烙铁、电热毯、电饭锅等用电器,由于电流通过时,电能全部转化为内能,故为纯电阻。 (√)
(3)电动机、电解槽等用电器,电流通过时电能除转化为内能外,还转化为其他形式的能,故为非纯电阻。 (√)
(4)不论纯电阻电路还是非纯电阻电路,计算焦耳热时仍可用P热=UI。 (×)
(5)不论何种电路,计算电功时均可用W=UIt。 (√)
2.关于电功和电热的计算,下列说法正确的是( )
A.如果是纯电阻电路,电功可用公式W=UIt计算,也可用公式W=I2Rt计算
B.如果是纯电阻电路,电热可用公式W=I2Rt计算,但不能用公式W=UIt计算
C.如果不是纯电阻电路,电功只能用公式W=I2Rt计算
D.如果不是纯电阻电路,电热可用公式W=I2Rt计算,也可用公式W=UIt计算
A [纯电阻电路,根据能量守恒,电功和电热相等,电功可用公式W=UIt计算,也可用公式W=I2Rt计算,故A正确,B错误;非纯电阻电路,电功用公式W=UIt计算,故C错误;非纯电阻电路,电热用公式W=I2Rt计算,故D错误。]
3.当电阻两端加上某一稳定电压时,通过该电阻的电荷量为0.3 C,消耗的电能为0.9 J。为在相同时间内使0.6 C的电荷量通过该电阻,在其两端需加的电压和消耗的电能分别是( )
A.3 V,1.8 J B.3 V,3.6 J
C.6 V,1.8 J D.6 V,3.6 J
D [根据公式W=Uq可知,当通过该电阻的电荷量为0.3 C,消耗的电能为0.9 J时,电阻的两端电压为3 V,此时的电流为I;若在相同时间内使0.6 C的电荷量通过该电阻,表明后者的电流是前者的二倍,则说明后者的电压也是前者的二倍,即在其两端需加的电压为3 V×2=6 V,消耗的电能为W=6 V×0.6 C=3.6 J,选项D正确。]
电功、电功率的理解和计算
在现代社会中,人们的生产、生活和科技实践活动都离不开电,各种各样的用电器减轻了人们的劳动强度,提高了工作效率,在享受电给我们带来方便的同时,你知道电能是如何转化为其他形式的能和电能在转化过程中满足怎样的规律吗?
提示:通过电流做功W=UIt。
1.对电功的理解
(1)从力的角度看,电流做功的实质是电场力对自由电荷做功。
(2)从能的角度看,电流做功过程是电能转化为其他形式的能的过程,电功的大小表示电能的减少量,标志着电能转化为其他形式的能的多少。
(3)电功W=UIt=qU对任何电路都适用。
2.串、并联电路中的功率关系
串联电路 并联电路
功率分配 = =
功率关系 P=P1+P2+…+Pn P=P1+P2+…+Pn
3.额定功率和实际功率
(1)用电器正常工作时所消耗的功率叫做额定功率。当用电器两端电压达到额定电压U额时,电流达到额定电流I额,电功率也达到额定功率P额,且P额=U额I额。
(2)用电器的实际功率是用电器在实际工作时消耗的电功率。为了使用电器不被烧毁,要求实际功率不能大于其额定功率。
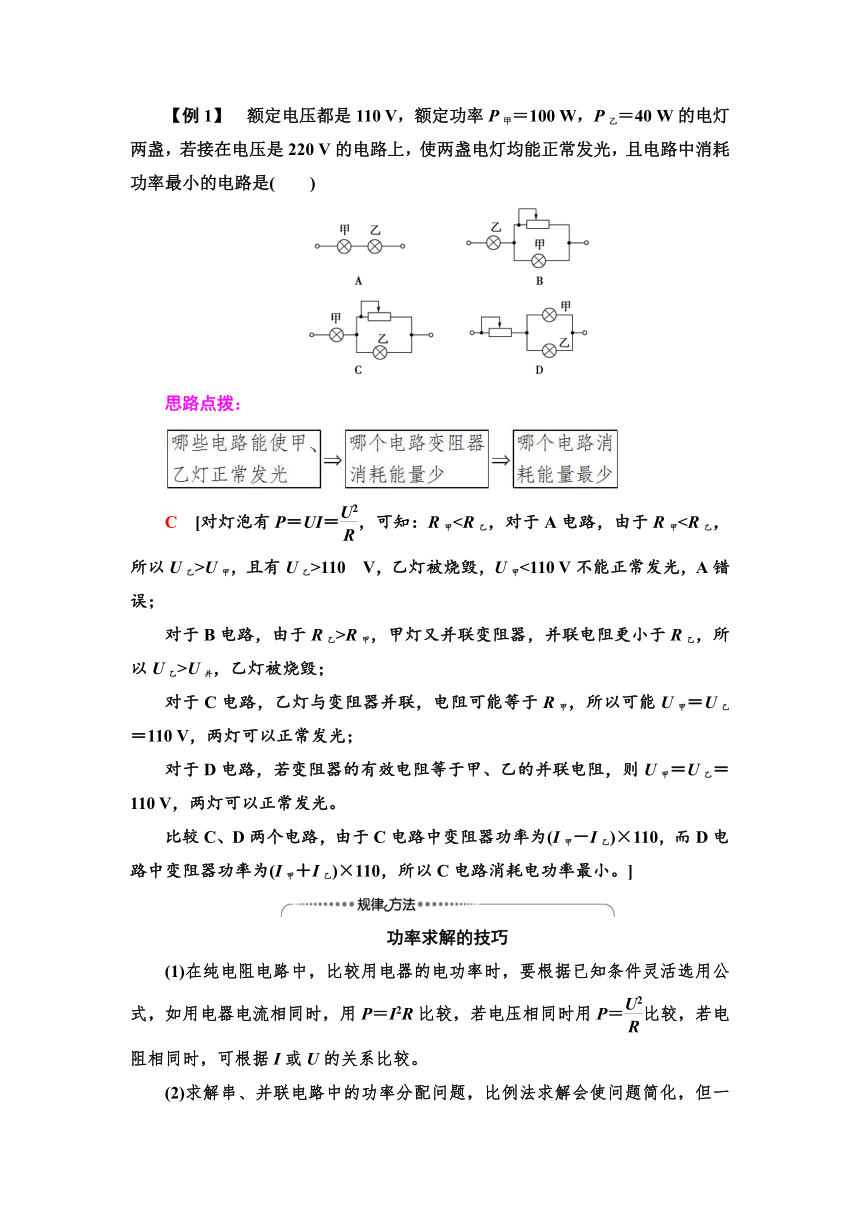
【例1】 额定电压都是110 V,额定功率P甲=100 W,P乙=40 W的电灯两盏,若接在电压是220 V的电路上,使两盏电灯均能正常发光,且电路中消耗功率最小的电路是( )
思路点拨:
C [对灯泡有P=UI=,可知:R甲U甲,且有U乙>110 V,乙灯被烧毁,U甲<110 V不能正常发光,A错误;
对于B电路,由于R乙>R甲,甲灯又并联变阻器,并联电阻更小于R乙,所以U乙>U并,乙灯被烧毁;
对于C电路,乙灯与变阻器并联,电阻可能等于R甲,所以可能U甲=U乙=110 V,两灯可以正常发光;
对于D电路,若变阻器的有效电阻等于甲、乙的并联电阻,则U甲=U乙=110 V,两灯可以正常发光。
比较C、D两个电路,由于C电路中变阻器功率为(I甲-I乙)×110,而D电路中变阻器功率为(I甲+I乙)×110,所以C电路消耗电功率最小。]
功率求解的技巧
(1)在纯电阻电路中,比较用电器的电功率时,要根据已知条件灵活选用公式,如用电器电流相同时,用P=I2R比较,若电压相同时用P=比较,若电阻相同时,可根据I或U的关系比较。
(2)求解串、并联电路中的功率分配问题,比例法求解会使问题简化,但一定要明确是正比还是反比关系。
(3)当求解用电器的功率时,要明确求解的是什么功率,实际功率与额定功率不一定相等。
1.电阻R1、R2的I?U图象如图所示,则下列说法正确的是( )
A.R1∶R2=3∶1
B.将R1与R2串联后接于电源上,则电压比U1∶U2=1∶3
C.将R1与R2并联后接于电源上,则电流比I1∶I2=1∶3
D.将R1与R2并联后接于电源上,则功率比P1∶P2=1∶3
B [由I?U图象可知R1∶R2=∶=1∶3,选项A错误;将R1与R2串联后接于电源上,则通过两电阻的电流相等,由欧姆定律U=IR可得U1∶U2=R1∶R2=1∶3,选项B正确;将R1与R2并联后接于电源上,则两电阻两端的电压相等,由欧姆定律I=可得I1∶I2=R2∶R1=3∶1,由P=可得P1∶P2=R2∶R1=3∶1,故选项C、D错误。]
电功与电热的比较
用电炉烧水时,炉盘内的电炉丝被烧得通红,产生大量的热,而连接电炉的导线却不怎么热,这是什么原因?
提示:通电导线跟电炉丝是串联在一起的,通过它们的电流相等,而电炉丝的电阻比连接电炉丝的导线电阻要大得多,由焦耳定律Q=I2Rt知在相等的时间内导线产生的热量比电炉丝产生的热量要少得多。
1.纯电阻电路和非纯电阻电路
(1)常用的电灯泡、电炉子等为纯电阻电路;电动机、电解槽等为非纯电阻电路。
(2)纯电阻电路服从欧姆定律,而非纯电阻电路不完全服从欧姆定律。
(3)纯电阻电路电流做功时,电能全部转化为电热;而非纯电阻电路,电流做功将电能一部分转化为电热,一部分转化为机械能或其他形式的能。
2.电功与电热
纯电阻电路 非纯电阻电路
电功 W=UIt=I2Rt=t W=UIt
电热 Q=UIt=I2Rt=t Q=I2Rt
关系 W=Q W>Q
3.电功率与热功率
纯电阻电路 非纯电阻电路
电功率 P电=UI=I2R= P电=UI
热功率 P热=UI=I2R= P热=I2R
关系 P电=P热 P电>P热
【例2】 规格为“220 V 36 W”的排气扇,线圈电阻为40 Ω,求:
(1)接上220 V的电压后,求排气扇转化为机械能的功率和发热的功率;
(2)如果接上220 V的电压后,扇叶被卡住,不能转动,求电动机消耗的功率和发热的功率。
思路点拨:(1)额定电压下,电流可据I=求出。
(2)机械功率可通过P机=P电-P热求出。
(3)电动机不工作时,220 V电压全加在40 Ω电阻上,电动机此时即为“电阻”。
[解析] (1)排气扇在220 V的电压下正常工作时的电流为:
I==A≈0.16 A,
发热功率为:
P热=I2R=(0.16)2×40 W≈1 W。
转化为机械能的功率为:
P机=P-P热=36 W-1 W=35 W。
(2)扇叶被卡住不能转动后,电动机成为纯电阻电路,电流做功全部转化为热能,此时电动机中电流为
I′==A=5.5 A,
电动机消耗的功率即发热功率:
P电′=P热′=UI′=220×5.5 W=1 210 W。
[答案] (1)35 W 1 W (2)1 210 W 1 210 W
电功、电热的计算方法
(1)判断电路中的用电器是纯电阻用电器还是非纯电阻用电器。
(2)分析各用电器之间的连接方式,对纯电阻电路,计算时可以利用串联电路的分压特点或并联电路的分流特点。
(3)由所求问题选取合适的公式,在非纯电阻电路中计算电功只能用W=UIt,计算电热只能用Q=I2Rt,欧姆定律的变形式在纯电阻电路中才能通用。
(4)对于含电动机的电路,电动机转动时是非纯电阻用电器,电动机不转动时是纯电阻用电器。
2.如图所示的电路中,输入电压U恒为12 V,灯泡L标有“6 V,12 W”字样,电动机线圈的电阻RM=0.5 Ω,若灯泡恰能正常发光,则下列说法中正确的是( )
A.电动机的总功率是72 W
B.电动机的热功率是1 W
C.电动机的输出功率是10 W
D.整个电路消耗的电功率是22 W
C [电动机两端的电压为U1=U-UL=(12-6) V=6 V,整个电路中的电流为I==2 A,所以电动机消耗功率为P=U1I=6×2 W=12 W,故A错误;电动机的热功率为P热=I2RM=22×0.5 W=2 W,故B错误;电动机的输出功率为P出=P-P热=(12-2) W=10 W,故C正确;整个电路消耗的功率为P总=UI=12×2 W=24 W,故D错误。]
电源的功率和效率
闭合电路中,电源电动势为E,内、外电路的电阻分别是r和R,电路中的电流为I,t时间内电源把多少其他形式的能转化为电能?外电路产生的热量是多少?内电路产生的热量是多少?三者之间有何关系?
提示:EIt I2Rt I2rt EIt=I2Rt+I2rt
1.电源的输出功率
P出=UI=I2R=R==,由此式可看出,当R=r时,P出有最大值,即Pm==。
2.讨论
如图所示。
(1)当R=r时,输出功率最大,P出=。
(2)当Rr时,若R增大,则P出减小。
(3)除R=r外,图象上总有两点输出功率P出相等,如图中R1与R2,则由()2×R1=()2×R2
整理得:R1R2=r2。
3.电源的效率
(1)定义:输出功率跟电路消耗的总功率的比值,
即η==。
(2)如果外电路为纯电阻电路,则η====,所以外电路电阻越大,电源效率越高。
(3)当电源输出功率最大时,R=r,η=50%。
【例3】 如图所示电路中,电池的电动势E=5 V,内电阻r=10 Ω,固定电阻R=90 Ω,R0是可变电阻,在R0由0增加到400 Ω的过程中,求:
(1)可变电阻R0上消耗功率最大的条件和最大热功率。
(2)电池的内电阻r和固定电阻R上消耗的最小热功率之和。
[解析] (1)可变电阻R0上消耗的热功率
P1=I2R0=()2R0=
=
由上式可得:当R0=100 Ω时,P1有最大值Pmax= W= W。
(2)r和R上消耗的热功率之和P2=I2(R+r)=×100
由上式可知,R0最大时,P2最小,即当R0=400 Ω时,P2有最小值P2min=×100 W=0.01 W。
[答案] (1)R0=100 Ω W (2)0.01 W
有关闭合电路中功率问题的三点提醒
(1)电源输出功率越大,效率不一定越高,如电源输出功率最大时,效率只有50%。
(2)判断可变电阻功率变化时,可将可变电阻以外的其他电阻看成电源的一部分内阻。
(3)当P输出3.将一个电源与一电阻箱连接构成闭合回路,测得的电阻箱所消耗的功率P与电阻箱的读数R的关系如图所示,下列说法正确的是( )
A.电源最大输出功率可能大于45 W
B.电源的内阻为5 Ω
C.电源的电动势为45 V
D.电阻箱消耗的功率为最大值时,电源的效率大于50%
B [由图可知,电源的输出功率最大为45 W,故A错误;当内外电阻相等时,电源的输出功率最大,由图可知,电源的内阻为5 Ω,故B正确;由Pmax=可知,E=30 V,故C错误;根据效率公式可得η=×100%,最大功率时内外电阻相等,所以效率为50%,故D错误。]
1.电炉通电后,电炉丝热得发红,而跟电炉连接的铜导线却不那么热,这是因为( )
A.通过铜导线的电流小,所以它消耗的电能也较少
B.电炉丝和铜导线消耗的电能相同,但铜导线散热快,所以就不那么热
C.通过电炉丝的电流大,所以它消耗的电能较多
D.铜导线电阻较小,所以它消耗的电能较少
D [电炉丝和铜导线是串联关系,故通过电炉丝的电流与通过铜导线的电流大小相等,电炉丝和铜导线在电学性能上的差别在于:前者的电阻大,后者的电阻很小,根据电流通过电阻发热的公式Q=I2Rt,在电流相同条件下,相同的时间内,电炉丝的发热量比铜导线上的发热量大得多。因此我们看到电炉通电后,电炉丝热得发红而与之相连的铜导线却不那么热,D正确。]
2.把两根电阻相同的电热丝先串联后并联分别接在同一电源上,若要产生相等的热量,则两种方法所需的时间之比t串:t并为( )
A.1∶1 B.2∶1 C.4∶1 D.1∶4
C [设每根电热丝电阻为R,则R串=2R,R并=,由Q=W=t得t串:t并=4∶1。]
3.(多选)如图所示,直线A为电源的U?I图线,直线B、C分别为电阻R1、R2的U?I图线。利用该电源分别与R1、R2组成闭合电路时,电源的输出功率分别为P1、P2,电源的效率分别为η1、η2,则( )
A.P1>P2 B.P1=P2
C.η1>η2 D.η1<η2
BC [两图线的交点表示把电阻接入电源的工作电流和外电压。
有,P1=U1I1=4×2 W=8 W
P2=U2I2=2×4 W=8 W
η1=×100%=×100%≈67%
η2=×100%=×100%≈33%。]
4.如图所示,直线OAC为某一直流电源的总功率随电流I变化的图线,曲线OBC表示同一直流电源内部的热功率随电流I变化的图线。若A、B点的横坐标均为1 A,那么AB线段表示的功率为( )
A.1 W B.6 W
C.2 W D.2.5 W
C [由题图可知,在C点,电源的总功率等于电源内部的热功率,所以电源的电动势为E=3 V,短路电流为I=3 A,所以电源的内阻为r==1 Ω,图象上AB段所表示的功率为PAB=P总-I2r=(1×3-12×1)W=2 W。]
5.小型直流电动机(其线圈内阻为r=1 Ω)与规格为“4 V 4 W”的小灯泡并联,再与阻值为R=5 Ω的电阻串联,然后接至U=12 V的电源上,如图所示,小灯泡恰好正常发光,电动机正常工作,求:
(1)通过电动机的电流。
(2)电动机的输出功率P出。
[解析] (1)流经灯泡的电流IL== A=1 A
流经电阻R的电流IR== A=1.6 A
流经电动机的电流I=IR-IL=0.6 A。
(2)电动机消耗的总功率P=IU=4×0.6 W=2.4 W
电动机的热功率P热=I2r=(0.6)2×1 W=0.36 W
电动机输出功率P出=P-P热=2.4 W-0.36 W=2.04 W。
[答案] (1)0.6 A (2)2.04 W
学习目标:1.[物理观念]理解电功、电功率的概念并能进行相关的计算。 2.[物理观念]知道焦耳定律,知道电功率与热功率的区别和联系。 3.[科学思维]知道纯电阻电路和非纯电阻电路的区别,会结合实际问题区分电功和电热。 4.[科学思维]理解闭合电路的各种功率及相关运算。
一、电功和电功率
1.电功
(1)定义:电流通过一段电路时,自由电荷在电场力的推动下做定向移动,电场力对自由电荷所做的功,称为电功。
(2)公式:W=UIt,单位:焦耳,符号:J。
2.电功率
(1)定义:电流做功与完成这些功所用时间之比叫做电功率。
(2)公式:P==UI,单位:瓦特,符号:W,1 kW=103 W。
二、焦耳定律
1.焦耳定律
(1)内容:电流通过导体产生的热量跟电流的二次方成正比,与导体的电阻及通电时间成正比。
(2)公式:Q=I2Rt。
2.热功率:一段电路因发热消耗的功率,P=I2R。
三、闭合电路中的能量
电源的功率 电源的输出功率 电源的内耗功率
公式 P=EI P出=U外I P内=U内I
意义 电源提供电能的功率 外电路消耗电能的功率 内电路消耗电能的功率
关系 P=P出+P内
1.正误判断(正确的打“√”,错误的打“×”)
(1)电流通过导体做的功越多,电功率越大。 (×)
(2)电炉、电烙铁、电热毯、电饭锅等用电器,由于电流通过时,电能全部转化为内能,故为纯电阻。 (√)
(3)电动机、电解槽等用电器,电流通过时电能除转化为内能外,还转化为其他形式的能,故为非纯电阻。 (√)
(4)不论纯电阻电路还是非纯电阻电路,计算焦耳热时仍可用P热=UI。 (×)
(5)不论何种电路,计算电功时均可用W=UIt。 (√)
2.关于电功和电热的计算,下列说法正确的是( )
A.如果是纯电阻电路,电功可用公式W=UIt计算,也可用公式W=I2Rt计算
B.如果是纯电阻电路,电热可用公式W=I2Rt计算,但不能用公式W=UIt计算
C.如果不是纯电阻电路,电功只能用公式W=I2Rt计算
D.如果不是纯电阻电路,电热可用公式W=I2Rt计算,也可用公式W=UIt计算
A [纯电阻电路,根据能量守恒,电功和电热相等,电功可用公式W=UIt计算,也可用公式W=I2Rt计算,故A正确,B错误;非纯电阻电路,电功用公式W=UIt计算,故C错误;非纯电阻电路,电热用公式W=I2Rt计算,故D错误。]
3.当电阻两端加上某一稳定电压时,通过该电阻的电荷量为0.3 C,消耗的电能为0.9 J。为在相同时间内使0.6 C的电荷量通过该电阻,在其两端需加的电压和消耗的电能分别是( )
A.3 V,1.8 J B.3 V,3.6 J
C.6 V,1.8 J D.6 V,3.6 J
D [根据公式W=Uq可知,当通过该电阻的电荷量为0.3 C,消耗的电能为0.9 J时,电阻的两端电压为3 V,此时的电流为I;若在相同时间内使0.6 C的电荷量通过该电阻,表明后者的电流是前者的二倍,则说明后者的电压也是前者的二倍,即在其两端需加的电压为3 V×2=6 V,消耗的电能为W=6 V×0.6 C=3.6 J,选项D正确。]
电功、电功率的理解和计算
在现代社会中,人们的生产、生活和科技实践活动都离不开电,各种各样的用电器减轻了人们的劳动强度,提高了工作效率,在享受电给我们带来方便的同时,你知道电能是如何转化为其他形式的能和电能在转化过程中满足怎样的规律吗?
提示:通过电流做功W=UIt。
1.对电功的理解
(1)从力的角度看,电流做功的实质是电场力对自由电荷做功。
(2)从能的角度看,电流做功过程是电能转化为其他形式的能的过程,电功的大小表示电能的减少量,标志着电能转化为其他形式的能的多少。
(3)电功W=UIt=qU对任何电路都适用。
2.串、并联电路中的功率关系
串联电路 并联电路
功率分配 = =
功率关系 P=P1+P2+…+Pn P=P1+P2+…+Pn
3.额定功率和实际功率
(1)用电器正常工作时所消耗的功率叫做额定功率。当用电器两端电压达到额定电压U额时,电流达到额定电流I额,电功率也达到额定功率P额,且P额=U额I额。
(2)用电器的实际功率是用电器在实际工作时消耗的电功率。为了使用电器不被烧毁,要求实际功率不能大于其额定功率。
【例1】 额定电压都是110 V,额定功率P甲=100 W,P乙=40 W的电灯两盏,若接在电压是220 V的电路上,使两盏电灯均能正常发光,且电路中消耗功率最小的电路是( )
思路点拨:
C [对灯泡有P=UI=,可知:R甲
对于B电路,由于R乙>R甲,甲灯又并联变阻器,并联电阻更小于R乙,所以U乙>U并,乙灯被烧毁;
对于C电路,乙灯与变阻器并联,电阻可能等于R甲,所以可能U甲=U乙=110 V,两灯可以正常发光;
对于D电路,若变阻器的有效电阻等于甲、乙的并联电阻,则U甲=U乙=110 V,两灯可以正常发光。
比较C、D两个电路,由于C电路中变阻器功率为(I甲-I乙)×110,而D电路中变阻器功率为(I甲+I乙)×110,所以C电路消耗电功率最小。]
功率求解的技巧
(1)在纯电阻电路中,比较用电器的电功率时,要根据已知条件灵活选用公式,如用电器电流相同时,用P=I2R比较,若电压相同时用P=比较,若电阻相同时,可根据I或U的关系比较。
(2)求解串、并联电路中的功率分配问题,比例法求解会使问题简化,但一定要明确是正比还是反比关系。
(3)当求解用电器的功率时,要明确求解的是什么功率,实际功率与额定功率不一定相等。
1.电阻R1、R2的I?U图象如图所示,则下列说法正确的是( )
A.R1∶R2=3∶1
B.将R1与R2串联后接于电源上,则电压比U1∶U2=1∶3
C.将R1与R2并联后接于电源上,则电流比I1∶I2=1∶3
D.将R1与R2并联后接于电源上,则功率比P1∶P2=1∶3
B [由I?U图象可知R1∶R2=∶=1∶3,选项A错误;将R1与R2串联后接于电源上,则通过两电阻的电流相等,由欧姆定律U=IR可得U1∶U2=R1∶R2=1∶3,选项B正确;将R1与R2并联后接于电源上,则两电阻两端的电压相等,由欧姆定律I=可得I1∶I2=R2∶R1=3∶1,由P=可得P1∶P2=R2∶R1=3∶1,故选项C、D错误。]
电功与电热的比较
用电炉烧水时,炉盘内的电炉丝被烧得通红,产生大量的热,而连接电炉的导线却不怎么热,这是什么原因?
提示:通电导线跟电炉丝是串联在一起的,通过它们的电流相等,而电炉丝的电阻比连接电炉丝的导线电阻要大得多,由焦耳定律Q=I2Rt知在相等的时间内导线产生的热量比电炉丝产生的热量要少得多。
1.纯电阻电路和非纯电阻电路
(1)常用的电灯泡、电炉子等为纯电阻电路;电动机、电解槽等为非纯电阻电路。
(2)纯电阻电路服从欧姆定律,而非纯电阻电路不完全服从欧姆定律。
(3)纯电阻电路电流做功时,电能全部转化为电热;而非纯电阻电路,电流做功将电能一部分转化为电热,一部分转化为机械能或其他形式的能。
2.电功与电热
纯电阻电路 非纯电阻电路
电功 W=UIt=I2Rt=t W=UIt
电热 Q=UIt=I2Rt=t Q=I2Rt
关系 W=Q W>Q
3.电功率与热功率
纯电阻电路 非纯电阻电路
电功率 P电=UI=I2R= P电=UI
热功率 P热=UI=I2R= P热=I2R
关系 P电=P热 P电>P热
【例2】 规格为“220 V 36 W”的排气扇,线圈电阻为40 Ω,求:
(1)接上220 V的电压后,求排气扇转化为机械能的功率和发热的功率;
(2)如果接上220 V的电压后,扇叶被卡住,不能转动,求电动机消耗的功率和发热的功率。
思路点拨:(1)额定电压下,电流可据I=求出。
(2)机械功率可通过P机=P电-P热求出。
(3)电动机不工作时,220 V电压全加在40 Ω电阻上,电动机此时即为“电阻”。
[解析] (1)排气扇在220 V的电压下正常工作时的电流为:
I==A≈0.16 A,
发热功率为:
P热=I2R=(0.16)2×40 W≈1 W。
转化为机械能的功率为:
P机=P-P热=36 W-1 W=35 W。
(2)扇叶被卡住不能转动后,电动机成为纯电阻电路,电流做功全部转化为热能,此时电动机中电流为
I′==A=5.5 A,
电动机消耗的功率即发热功率:
P电′=P热′=UI′=220×5.5 W=1 210 W。
[答案] (1)35 W 1 W (2)1 210 W 1 210 W
电功、电热的计算方法
(1)判断电路中的用电器是纯电阻用电器还是非纯电阻用电器。
(2)分析各用电器之间的连接方式,对纯电阻电路,计算时可以利用串联电路的分压特点或并联电路的分流特点。
(3)由所求问题选取合适的公式,在非纯电阻电路中计算电功只能用W=UIt,计算电热只能用Q=I2Rt,欧姆定律的变形式在纯电阻电路中才能通用。
(4)对于含电动机的电路,电动机转动时是非纯电阻用电器,电动机不转动时是纯电阻用电器。
2.如图所示的电路中,输入电压U恒为12 V,灯泡L标有“6 V,12 W”字样,电动机线圈的电阻RM=0.5 Ω,若灯泡恰能正常发光,则下列说法中正确的是( )
A.电动机的总功率是72 W
B.电动机的热功率是1 W
C.电动机的输出功率是10 W
D.整个电路消耗的电功率是22 W
C [电动机两端的电压为U1=U-UL=(12-6) V=6 V,整个电路中的电流为I==2 A,所以电动机消耗功率为P=U1I=6×2 W=12 W,故A错误;电动机的热功率为P热=I2RM=22×0.5 W=2 W,故B错误;电动机的输出功率为P出=P-P热=(12-2) W=10 W,故C正确;整个电路消耗的功率为P总=UI=12×2 W=24 W,故D错误。]
电源的功率和效率
闭合电路中,电源电动势为E,内、外电路的电阻分别是r和R,电路中的电流为I,t时间内电源把多少其他形式的能转化为电能?外电路产生的热量是多少?内电路产生的热量是多少?三者之间有何关系?
提示:EIt I2Rt I2rt EIt=I2Rt+I2rt
1.电源的输出功率
P出=UI=I2R=R==,由此式可看出,当R=r时,P出有最大值,即Pm==。
2.讨论
如图所示。
(1)当R=r时,输出功率最大,P出=。
(2)当R
(3)除R=r外,图象上总有两点输出功率P出相等,如图中R1与R2,则由()2×R1=()2×R2
整理得:R1R2=r2。
3.电源的效率
(1)定义:输出功率跟电路消耗的总功率的比值,
即η==。
(2)如果外电路为纯电阻电路,则η====,所以外电路电阻越大,电源效率越高。
(3)当电源输出功率最大时,R=r,η=50%。
【例3】 如图所示电路中,电池的电动势E=5 V,内电阻r=10 Ω,固定电阻R=90 Ω,R0是可变电阻,在R0由0增加到400 Ω的过程中,求:
(1)可变电阻R0上消耗功率最大的条件和最大热功率。
(2)电池的内电阻r和固定电阻R上消耗的最小热功率之和。
[解析] (1)可变电阻R0上消耗的热功率
P1=I2R0=()2R0=
=
由上式可得:当R0=100 Ω时,P1有最大值Pmax= W= W。
(2)r和R上消耗的热功率之和P2=I2(R+r)=×100
由上式可知,R0最大时,P2最小,即当R0=400 Ω时,P2有最小值P2min=×100 W=0.01 W。
[答案] (1)R0=100 Ω W (2)0.01 W
有关闭合电路中功率问题的三点提醒
(1)电源输出功率越大,效率不一定越高,如电源输出功率最大时,效率只有50%。
(2)判断可变电阻功率变化时,可将可变电阻以外的其他电阻看成电源的一部分内阻。
(3)当P输出
A.电源最大输出功率可能大于45 W
B.电源的内阻为5 Ω
C.电源的电动势为45 V
D.电阻箱消耗的功率为最大值时,电源的效率大于50%
B [由图可知,电源的输出功率最大为45 W,故A错误;当内外电阻相等时,电源的输出功率最大,由图可知,电源的内阻为5 Ω,故B正确;由Pmax=可知,E=30 V,故C错误;根据效率公式可得η=×100%,最大功率时内外电阻相等,所以效率为50%,故D错误。]
1.电炉通电后,电炉丝热得发红,而跟电炉连接的铜导线却不那么热,这是因为( )
A.通过铜导线的电流小,所以它消耗的电能也较少
B.电炉丝和铜导线消耗的电能相同,但铜导线散热快,所以就不那么热
C.通过电炉丝的电流大,所以它消耗的电能较多
D.铜导线电阻较小,所以它消耗的电能较少
D [电炉丝和铜导线是串联关系,故通过电炉丝的电流与通过铜导线的电流大小相等,电炉丝和铜导线在电学性能上的差别在于:前者的电阻大,后者的电阻很小,根据电流通过电阻发热的公式Q=I2Rt,在电流相同条件下,相同的时间内,电炉丝的发热量比铜导线上的发热量大得多。因此我们看到电炉通电后,电炉丝热得发红而与之相连的铜导线却不那么热,D正确。]
2.把两根电阻相同的电热丝先串联后并联分别接在同一电源上,若要产生相等的热量,则两种方法所需的时间之比t串:t并为( )
A.1∶1 B.2∶1 C.4∶1 D.1∶4
C [设每根电热丝电阻为R,则R串=2R,R并=,由Q=W=t得t串:t并=4∶1。]
3.(多选)如图所示,直线A为电源的U?I图线,直线B、C分别为电阻R1、R2的U?I图线。利用该电源分别与R1、R2组成闭合电路时,电源的输出功率分别为P1、P2,电源的效率分别为η1、η2,则( )
A.P1>P2 B.P1=P2
C.η1>η2 D.η1<η2
BC [两图线的交点表示把电阻接入电源的工作电流和外电压。
有,P1=U1I1=4×2 W=8 W
P2=U2I2=2×4 W=8 W
η1=×100%=×100%≈67%
η2=×100%=×100%≈33%。]
4.如图所示,直线OAC为某一直流电源的总功率随电流I变化的图线,曲线OBC表示同一直流电源内部的热功率随电流I变化的图线。若A、B点的横坐标均为1 A,那么AB线段表示的功率为( )
A.1 W B.6 W
C.2 W D.2.5 W
C [由题图可知,在C点,电源的总功率等于电源内部的热功率,所以电源的电动势为E=3 V,短路电流为I=3 A,所以电源的内阻为r==1 Ω,图象上AB段所表示的功率为PAB=P总-I2r=(1×3-12×1)W=2 W。]
5.小型直流电动机(其线圈内阻为r=1 Ω)与规格为“4 V 4 W”的小灯泡并联,再与阻值为R=5 Ω的电阻串联,然后接至U=12 V的电源上,如图所示,小灯泡恰好正常发光,电动机正常工作,求:
(1)通过电动机的电流。
(2)电动机的输出功率P出。
[解析] (1)流经灯泡的电流IL== A=1 A
流经电阻R的电流IR== A=1.6 A
流经电动机的电流I=IR-IL=0.6 A。
(2)电动机消耗的总功率P=IU=4×0.6 W=2.4 W
电动机的热功率P热=I2r=(0.6)2×1 W=0.36 W
电动机输出功率P出=P-P热=2.4 W-0.36 W=2.04 W。
[答案] (1)0.6 A (2)2.04 W
同课章节目录
- 第一章 静电场的描述
- 第一节 静电现象
- 第二节 库仑定律
- 第三节 电场 电场强度
- 第四节 电势能与电势
- 第五节 电势差及其与电场强度的关系
- 第二章 静电场的应用
- 第一节 电容器与电容
- 第二节 带电粒子在电场中的运动
- 第三节 静电的利用与防护
- 第三章 恒定电流
- 第一节 导体的伏安特性曲线
- 第二节 决定导体电阻大小的因素
- 第三节 测量金属丝的电阻率
- 第四节 电阻的串联和并联
- 第四章 闭合电路
- 第一节 常见的电路元器件
- 第二节 闭合电路的欧姆定律
- 第三节 测量电源的电动势和内阻
- 第四节 练习使用多用电表
- 第五节 家庭电路与安全用电
- 第五章 电能与能源的可持续发展
- 第一节 电路中的能量
- 第二节 能源的利用方式
- 第三节 能量的转化与守恒
- 第四节 能源与环境
- 第六章 电磁现象与电磁波
- 第一节 磁现象与磁场
- 第二节 磁感应强度
- 第三节 电磁感应现象
- 第四节 电磁波及其应用
- 第五节 量子化现象
