2.3二次函数与一元二次方程,不等式(1)(18张PPT)
文档属性
| 名称 | 2.3二次函数与一元二次方程,不等式(1)(18张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-20 21:51:00 | ||
图片预览






文档简介
(共18张PPT)
第二章
一元二次函数、方程和不等式
情境导学
问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24m,围成的矩形区域的面积要大于20m2,则这个矩形的边长为多少米?
情境导学
设这个矩形的一条边长为xm,则另一条边长为(12-x)m.
由题意,得:(12-x)x>20,
其中x∈{x|0<x<12}.
整理得
x2-12x+20<0,x∈{x|0<x<12}.
①
求得不等式①的解集,就得到了问题的答案.
我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.
1.一元二次不等式的定义:
一元二次不等式的一般表达式ax2+bx+c>0
(a≠0)
或ax2+bx+c<0
(a≠0),其中a,b,c均为常数.
概念解析
2.零点的定义
一般地,对于二次函数y=ax2+bx+c(a≠0),把使ax2+bx+c=0
的实数x叫做二次函数y=ax2+bx+c零点。
(3).由图象写出
不等式x2-x-6>0
的解集为
————————
不等式x2-x-6<0
的解集为
————————
(1).图象与x轴交点的坐标为___________,
方程x2-x-6=0的解是______
该坐标与方程的解有什么关系:
______________________
(2).当x取
__________
时,y=0?
当x取
__________
时,y>0?
当x取
__________
时,y<0?
交点的横坐标即为方程的根
1、作二次函数y=x2-x-6的图象。它的对应值表与图像如下:
-2
3
y>0
y>0
y<0
y
x
o
(-2,0)
(3,0)
x=
-2
或3
x<-2
或
x>3
-2﹛x|x<-2或x>3﹜
﹛x|-2x
-3
-2
-1
0
1
2
3
4
y
6
0
-4
-6
-6
-4
0
6
y=x2-x-6
x=-2,x=3
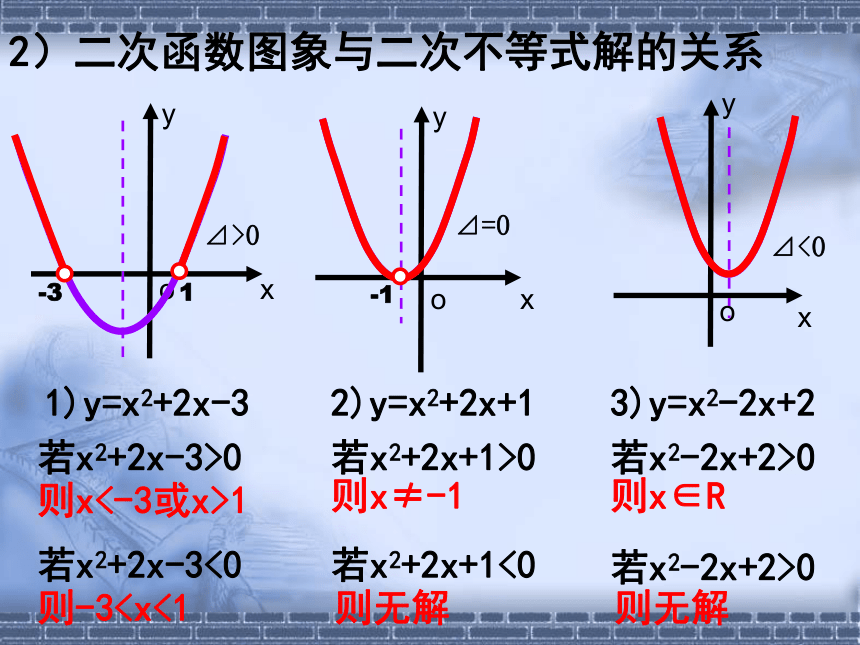
2)二次函数图象与二次不等式解的关系
⊿=0
o
x
y
⊿>0
o
x
y
⊿<0
o
x
y
1)y=x2+2x-3
2)y=x2+2x+1
3)y=x2-2x+2
若x2+2x-3>0
-3
1
-1
若x2+2x-3<0
若x2+2x+1>0
若x2+2x+1<0
则x<-3或x>1
则-3则x≠-1
则无解
若x2-2x+2>0
则x∈R
则无解
若x2-2x+2>0
2、总结结论:“三个二次”的关系
x1
x2
⊿=b2-4ac
二次函数
y=ax2+bx+c(a>0)
的图象
方程ax2+bx+c=0
的根
ax2+bx+c>0(a>0)
的解集
ax2+bx+c<0
(a>0)
的解集
x1(x2)
⊿>0
⊿=0
⊿<0
有两个不等实根
x1,x2(x1﹛x|xx2﹜
﹛x|x1有两个相等实根x1=x2
无实根
﹛x|x≠x1﹜
Φ
Φ
R
例1:解不等式:
x2-2x-15≥0
原不等式变形为(x+3)(x-5)
≥
0
方程(x+3)(x-5)=0的
两根为:
x=-3,或x=5
∴
不等式的解集
为:{x│
x
≤-3
或x
≥5}。
y
-3
5
0
x
。
。
解:
先求方程的根
画函数的图象
写出解集
典例解析
例2:解不等式-
x2
+
2x
–
3
>0
解:整理,得
x2
-
2x
+
3
<
0
因为△=
4
-
12
=
-
8
<
0
方程
2
x2
-
3x
–
2
=
0无实数根
所以原不等式的解集为ф
【点评】
若a<0时,先二次项系数化正!
典例解析
解:
典例解析
结合以上例题总结:
1、求解一元二次不等式的步骤是什么?
2、解一元二次不等式中常见的错误是什么?应如何避免?
归纳总结
(1)化成标准形式
ax2+bx+c>0(a>0)
ax2+bx+c<0
(a>0)
(2)
看能否因式分解,不能分解的计算△,
(3)
求出方程ax2+bx+c=0
的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.
解一元二次不等式ax2+bx+c>0、ax2+bx+c<0
(a>0)的步骤:
归纳总结
解:整理,得6x2+x-2
0
因为⊿=1+48=49>0
方程6x2+x-2=0的解是
x1=
-2/3,x2=1/2
所以原不等式的解集为:
{x|x
-2/3或x
1/2
}
(2)–6x2-x+2
0
课堂练习1.解下列不等式
?
解:因为⊿=49-24=25>0
方程3x2-7x+2=0的解是
x1=1/3,x2=2
所以原不等式的解集为
﹛x|1/3(1)3x2-7x+2<0
?
(3)4x2+4x+1<0
解:因为⊿=42-4
4=0
方程4x2+4x+1=0的根为
x1=x2=-1/2
所以原不等式的
解集为?
(4)x2-3x+5>0
解:因为⊿=9-20<0
方程x2-3x+5=0无解
所以原不等式的
解集为R
2)函数值是正数,即x2-4x+1>0,解得:
,即,当
时,原函数的值是正数。
解:1)函数值等于0,即x2-4x+1=0,解得:
即,当
时,原函数的值等于0。
课堂练习2.
x是什么实数时,函数y=x2-4x+1的值
(1)
等于0?
(2)
是正数?
(3)
是负数?
3)函数值是负数,即x2-4x+1<0,解得:
,即,当
时,原函数的值是负数。
课堂练习3.
是什么实数时,
有意义?
解:要想原式有意义,即要使
,
解这个不等式得:{x|x<-4或x>3}
所以,原式当x<-4或x>3时有意义。
作业
P21
习题1.5
1.
(1)(2)(3)(4)
3.
(1)(2)(3)(4)
再
见
第二章
一元二次函数、方程和不等式
情境导学
问题 园艺师打算在绿地上用栅栏围一个矩形区域种植花卉.若栅栏的长度是24m,围成的矩形区域的面积要大于20m2,则这个矩形的边长为多少米?
情境导学
设这个矩形的一条边长为xm,则另一条边长为(12-x)m.
由题意,得:(12-x)x>20,
其中x∈{x|0<x<12}.
整理得
x2-12x+20<0,x∈{x|0<x<12}.
①
求得不等式①的解集,就得到了问题的答案.
我们把只含有一个未知数,并且未知数的最高次数是2的不等式,称为一元二次不等式.
1.一元二次不等式的定义:
一元二次不等式的一般表达式ax2+bx+c>0
(a≠0)
或ax2+bx+c<0
(a≠0),其中a,b,c均为常数.
概念解析
2.零点的定义
一般地,对于二次函数y=ax2+bx+c(a≠0),把使ax2+bx+c=0
的实数x叫做二次函数y=ax2+bx+c零点。
(3).由图象写出
不等式x2-x-6>0
的解集为
————————
不等式x2-x-6<0
的解集为
————————
(1).图象与x轴交点的坐标为___________,
方程x2-x-6=0的解是______
该坐标与方程的解有什么关系:
______________________
(2).当x取
__________
时,y=0?
当x取
__________
时,y>0?
当x取
__________
时,y<0?
交点的横坐标即为方程的根
1、作二次函数y=x2-x-6的图象。它的对应值表与图像如下:
-2
3
y>0
y>0
y<0
y
x
o
(-2,0)
(3,0)
x=
-2
或3
x<-2
或
x>3
-2
﹛x|-2
-3
-2
-1
0
1
2
3
4
y
6
0
-4
-6
-6
-4
0
6
y=x2-x-6
x=-2,x=3
2)二次函数图象与二次不等式解的关系
⊿=0
o
x
y
⊿>0
o
x
y
⊿<0
o
x
y
1)y=x2+2x-3
2)y=x2+2x+1
3)y=x2-2x+2
若x2+2x-3>0
-3
1
-1
若x2+2x-3<0
若x2+2x+1>0
若x2+2x+1<0
则x<-3或x>1
则-3
则无解
若x2-2x+2>0
则x∈R
则无解
若x2-2x+2>0
2、总结结论:“三个二次”的关系
x1
x2
⊿=b2-4ac
二次函数
y=ax2+bx+c(a>0)
的图象
方程ax2+bx+c=0
的根
ax2+bx+c>0(a>0)
的解集
ax2+bx+c<0
(a>0)
的解集
x1(x2)
⊿>0
⊿=0
⊿<0
有两个不等实根
x1,x2(x1
﹛x|x1
无实根
﹛x|x≠x1﹜
Φ
Φ
R
例1:解不等式:
x2-2x-15≥0
原不等式变形为(x+3)(x-5)
≥
0
方程(x+3)(x-5)=0的
两根为:
x=-3,或x=5
∴
不等式的解集
为:{x│
x
≤-3
或x
≥5}。
y
-3
5
0
x
。
。
解:
先求方程的根
画函数的图象
写出解集
典例解析
例2:解不等式-
x2
+
2x
–
3
>0
解:整理,得
x2
-
2x
+
3
<
0
因为△=
4
-
12
=
-
8
<
0
方程
2
x2
-
3x
–
2
=
0无实数根
所以原不等式的解集为ф
【点评】
若a<0时,先二次项系数化正!
典例解析
解:
典例解析
结合以上例题总结:
1、求解一元二次不等式的步骤是什么?
2、解一元二次不等式中常见的错误是什么?应如何避免?
归纳总结
(1)化成标准形式
ax2+bx+c>0(a>0)
ax2+bx+c<0
(a>0)
(2)
看能否因式分解,不能分解的计算△,
(3)
求出方程ax2+bx+c=0
的实根;(画出函数图像)
(4)(结合函数图象)写出不等式的解集.
解一元二次不等式ax2+bx+c>0、ax2+bx+c<0
(a>0)的步骤:
归纳总结
解:整理,得6x2+x-2
0
因为⊿=1+48=49>0
方程6x2+x-2=0的解是
x1=
-2/3,x2=1/2
所以原不等式的解集为:
{x|x
-2/3或x
1/2
}
(2)–6x2-x+2
0
课堂练习1.解下列不等式
?
解:因为⊿=49-24=25>0
方程3x2-7x+2=0的解是
x1=1/3,x2=2
所以原不等式的解集为
﹛x|1/3
?
(3)4x2+4x+1<0
解:因为⊿=42-4
4=0
方程4x2+4x+1=0的根为
x1=x2=-1/2
所以原不等式的
解集为?
(4)x2-3x+5>0
解:因为⊿=9-20<0
方程x2-3x+5=0无解
所以原不等式的
解集为R
2)函数值是正数,即x2-4x+1>0,解得:
,即,当
时,原函数的值是正数。
解:1)函数值等于0,即x2-4x+1=0,解得:
即,当
时,原函数的值等于0。
课堂练习2.
x是什么实数时,函数y=x2-4x+1的值
(1)
等于0?
(2)
是正数?
(3)
是负数?
3)函数值是负数,即x2-4x+1<0,解得:
,即,当
时,原函数的值是负数。
课堂练习3.
是什么实数时,
有意义?
解:要想原式有意义,即要使
,
解这个不等式得:{x|x<-4或x>3}
所以,原式当x<-4或x>3时有意义。
作业
P21
习题1.5
1.
(1)(2)(3)(4)
3.
(1)(2)(3)(4)
再
见
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
