六年级上册数学教案-3.3 分数除以分数苏教版
文档属性
| 名称 | 六年级上册数学教案-3.3 分数除以分数苏教版 |

|
|
| 格式 | doc | ||
| 文件大小 | 132.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览

文档简介
分数除以分数
教材简介:本课是在学习了分数除以整数和整数除以分数的基础上进行的,学生已经初步感受到一个数除以另一个数时要变除为乘,去乘除数的倒数。本课则是进一步丰富分数除法的内涵,扩展到分数除以分数,并由此统一分数除法的法则。教材意图让学生利用知识的迁移得出分数除以分数的计算方法,并用一些直观的手段来验证此思路是正确的。练习中,还安排了一些旨在探讨分数除法中的规律(当除数大于1、小于1或等于1时,商相应地小于、大于或等于被除数)的内容。
教学目标:
1、理解分数除以分数计算法则的推导过程,掌握分数除以分数的计算方法。
2、在此基础上归纳出分数除法统一的运算法则。
3、教学过程中鼓励学生自觉运用化归的数学思想方法解决新问题。
教学重难点:
重点:理解分数除以分数的计算方法,能正确地进行计算;并能总结、归纳出分数除法的计算法则。
难点:根据除数的特点判断商和被除数之间的关系。
教学设计
一、回忆导入
同学们,最近我们学习了“分数除法”,学了哪些类型?
生1:有分数除以整数的。(贴板书)师:举个例子。
生2:还有整数除以分数的。(贴板书)师:比如说……
会计算吗?谁来说说怎么算?(指名说一说分数除以整数和整数除以分数的计算方法)
师:这两题的计算方法好象有相同的地方,大家看出来了吗?(学生交流)生:都把除号变成乘号,然后把除数变成它的倒数。
师:没错,都把分数除法转化成我们已经学过的分数乘法来算了。(贴板书:分数乘法)“转化”这个方法在数学里经常用到,通常我们都会把一些新问题转化为已经学过的旧知识来解决。
师:你们猜猜,还会有其他类型的分数除法吗?(分数除以分数)我们一起来看。
【设计意图:迅速唤醒学生的旧知,为知识的迁移创造一种条件。】
二、 创设情境,推导算法。
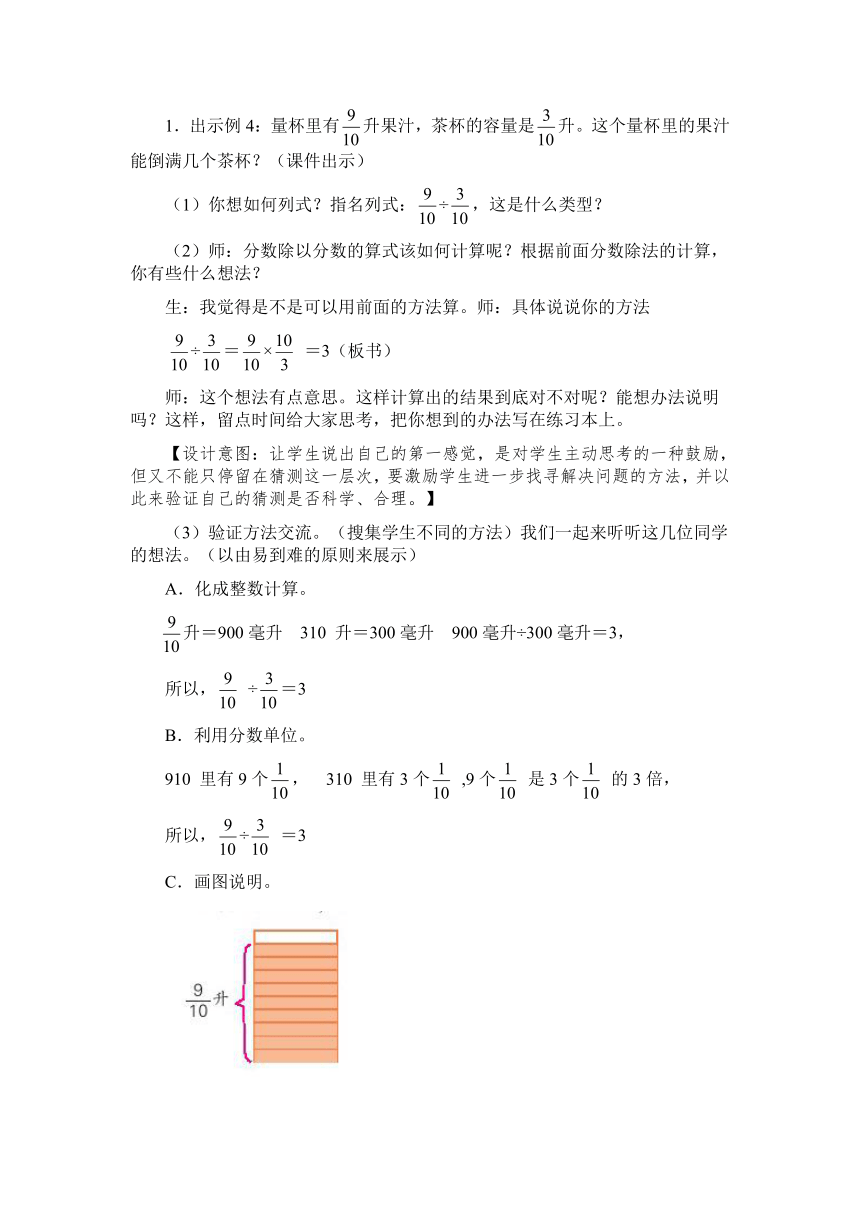
1.出示例4:量杯里有升果汁,茶杯的容量是升。这个量杯里的果汁能倒满几个茶杯?(课件出示)
(1)你想如何列式?指名列式:÷,这是什么类型?
(2)师:分数除以分数的算式该如何计算呢?根据前面分数除法的计算,你有些什么想法?
生:我觉得是不是可以用前面的方法算。师:具体说说你的方法
÷=× =3(板书)
师:这个想法有点意思。这样计算出的结果到底对不对呢?能想办法说明吗?这样,留点时间给大家思考,把你想到的办法写在练习本上。
【设计意图:让学生说出自己的第一感觉,是对学生主动思考的一种鼓励,但又不能只停留在猜测这一层次,要激励学生进一步找寻解决问题的方法,并以此来验证自己的猜测是否科学、合理。】
(3)验证方法交流。(搜集学生不同的方法)我们一起来听听这几位同学的想法。(以由易到难的原则来展示)
A.化成整数计算。
升=900毫升 310 升=300毫升 900毫升÷300毫升=3,
所以, ÷=3
B.利用分数单位。
910 里有9个, 310 里有3个 ,9个 是3个 的3倍,
所以,÷ =3
C.画图说明。
D.化成小数计算。
=0.9,=0.3,0.9÷0.3=3
【设计意图:学生验证自己的猜测,既可以用化归这一数学思想方法,将新问题转化成已经掌握的旧知识来进行,也可以通过直观的图画来得出结论。我们确信学生有这种能力。教师在倾听学生讨论时可以及时地根据他们的讨论情况相机提出一些指导性意见,对学生提出的有创意的见解要给与充分的褒奖。以此来强化学生从事创新活动的动机。经历这样的学习过程,学生的学习信心无疑会得到增强,并乐于在今后的学习中运用“观察比较——提出猜测——探索验证——解决问题”这一学习策略。】
2. 总结计算方法。
师:刚刚大家用不同的方法算出了结果,这个结果和直接用除法计算得出的结果一样吗?这说明了什么?(分数除以分数可以用以前分数除以整数或整数除以分数的方法来计算。)
师:我们一起回顾一下,分数除以分数,是如何直接计算的?(老师引导学生看算式÷=× =3)
现在将我们的视线看向这3种不同类型的分数除法,对比一下计算方法,你有什么发现?
生可能:我发现他们的计算方法都一样。师,能具体说说吗?(多让一些孩子说3-4个)
生可能总结:被除数除以除数,等于被除数乘除数的倒数。
师:说得挺好。这里的被除数和除数,我们也可以换个说法,叫它甲数、乙数。那这个计算方法又可以说成……(甲数除以乙数,等于甲数乘乙数的倒数。) 还可以说成……
师:大家的说法虽各不相同,但其实都是把分数除法转化成分数乘法来算,具体是怎么转化的?
【设计意图:心理学研究证明,当将一个知识寓于完整的系统之中时,更易于学习者去理解记忆、去把握运用。因此,及时地将分数除以整数、整数除以分数和分数除以分数的计算方法归纳成一个有机的整体,更有助于学生的理解和掌握。对于学生而言,这是一种思维上的提升,越是简洁的东西,越是具有普遍适应性。】
三、 练习巩固,掌握算法。
1.基础练习
现在你会计算分数除以分数了吗?
检验一下 ÷ ÷
大家在练习本上计算,你们都是怎么算的?叫几个同学展示方法。
2.这些算式都缺少了一部分,能填完整吗?
÷=( )( )
÷( )=×
÷=( )×
÷( )=×( )
这两空所填的数有什么关系?如果第一空填a,第二空填什么?
想一想 这个a可以表示所有的数吗?为什么?看来,我们刚刚总结的计算方法里,还需强调一下(0除外)这个要求。
3.总结提升,探索规律。
我们再来算几道题。(逐题出示,学生计算后直接报结果)将计算过程写在练习本上。
出示÷3=,÷=,÷2=比一比他们的商与被除数,你有什么发现?生:商都比被除数小。你能再举几个商比被除数小的例子吗?(举例并计算)师:这些算式中,是哪一个数影响着商的大小(除数),什么情况下,商会小于被除数?(当除数大于1时,商小于被除数)什么情况下,商会等于被除数?(当除数等于1时,商等于被除数;)什么情况下,商又会大于被除数呢?(当除数小于1时,商大于被除数。)(举例说明)
需要注意的是这里的被除数和除数都不为0 。
【设计意图:此内容的安排,已经不满足于简单的方法运用这一层次,而是引导学生建立一种宏观视野,在熟练运用计算方法时,还应注意到结果的变化是有缘由的,也就是一种更高的系统化。】
四、 总结全课。
回顾整节课,我们一起学习了不少内容,看,老师在黑板上写下这么多的板书,你最想留下的是什么? 为什么?
板书设计
转化
分数除法——分数乘法
分数除以整数
学生列式
整数除以分数
学生列式
分数除以分数
÷ = × =3
甲数÷ 乙数 = 甲数× 乙数的倒数
(0除外)
教材简介:本课是在学习了分数除以整数和整数除以分数的基础上进行的,学生已经初步感受到一个数除以另一个数时要变除为乘,去乘除数的倒数。本课则是进一步丰富分数除法的内涵,扩展到分数除以分数,并由此统一分数除法的法则。教材意图让学生利用知识的迁移得出分数除以分数的计算方法,并用一些直观的手段来验证此思路是正确的。练习中,还安排了一些旨在探讨分数除法中的规律(当除数大于1、小于1或等于1时,商相应地小于、大于或等于被除数)的内容。
教学目标:
1、理解分数除以分数计算法则的推导过程,掌握分数除以分数的计算方法。
2、在此基础上归纳出分数除法统一的运算法则。
3、教学过程中鼓励学生自觉运用化归的数学思想方法解决新问题。
教学重难点:
重点:理解分数除以分数的计算方法,能正确地进行计算;并能总结、归纳出分数除法的计算法则。
难点:根据除数的特点判断商和被除数之间的关系。
教学设计
一、回忆导入
同学们,最近我们学习了“分数除法”,学了哪些类型?
生1:有分数除以整数的。(贴板书)师:举个例子。
生2:还有整数除以分数的。(贴板书)师:比如说……
会计算吗?谁来说说怎么算?(指名说一说分数除以整数和整数除以分数的计算方法)
师:这两题的计算方法好象有相同的地方,大家看出来了吗?(学生交流)生:都把除号变成乘号,然后把除数变成它的倒数。
师:没错,都把分数除法转化成我们已经学过的分数乘法来算了。(贴板书:分数乘法)“转化”这个方法在数学里经常用到,通常我们都会把一些新问题转化为已经学过的旧知识来解决。
师:你们猜猜,还会有其他类型的分数除法吗?(分数除以分数)我们一起来看。
【设计意图:迅速唤醒学生的旧知,为知识的迁移创造一种条件。】
二、 创设情境,推导算法。
1.出示例4:量杯里有升果汁,茶杯的容量是升。这个量杯里的果汁能倒满几个茶杯?(课件出示)
(1)你想如何列式?指名列式:÷,这是什么类型?
(2)师:分数除以分数的算式该如何计算呢?根据前面分数除法的计算,你有些什么想法?
生:我觉得是不是可以用前面的方法算。师:具体说说你的方法
÷=× =3(板书)
师:这个想法有点意思。这样计算出的结果到底对不对呢?能想办法说明吗?这样,留点时间给大家思考,把你想到的办法写在练习本上。
【设计意图:让学生说出自己的第一感觉,是对学生主动思考的一种鼓励,但又不能只停留在猜测这一层次,要激励学生进一步找寻解决问题的方法,并以此来验证自己的猜测是否科学、合理。】
(3)验证方法交流。(搜集学生不同的方法)我们一起来听听这几位同学的想法。(以由易到难的原则来展示)
A.化成整数计算。
升=900毫升 310 升=300毫升 900毫升÷300毫升=3,
所以, ÷=3
B.利用分数单位。
910 里有9个, 310 里有3个 ,9个 是3个 的3倍,
所以,÷ =3
C.画图说明。
D.化成小数计算。
=0.9,=0.3,0.9÷0.3=3
【设计意图:学生验证自己的猜测,既可以用化归这一数学思想方法,将新问题转化成已经掌握的旧知识来进行,也可以通过直观的图画来得出结论。我们确信学生有这种能力。教师在倾听学生讨论时可以及时地根据他们的讨论情况相机提出一些指导性意见,对学生提出的有创意的见解要给与充分的褒奖。以此来强化学生从事创新活动的动机。经历这样的学习过程,学生的学习信心无疑会得到增强,并乐于在今后的学习中运用“观察比较——提出猜测——探索验证——解决问题”这一学习策略。】
2. 总结计算方法。
师:刚刚大家用不同的方法算出了结果,这个结果和直接用除法计算得出的结果一样吗?这说明了什么?(分数除以分数可以用以前分数除以整数或整数除以分数的方法来计算。)
师:我们一起回顾一下,分数除以分数,是如何直接计算的?(老师引导学生看算式÷=× =3)
现在将我们的视线看向这3种不同类型的分数除法,对比一下计算方法,你有什么发现?
生可能:我发现他们的计算方法都一样。师,能具体说说吗?(多让一些孩子说3-4个)
生可能总结:被除数除以除数,等于被除数乘除数的倒数。
师:说得挺好。这里的被除数和除数,我们也可以换个说法,叫它甲数、乙数。那这个计算方法又可以说成……(甲数除以乙数,等于甲数乘乙数的倒数。) 还可以说成……
师:大家的说法虽各不相同,但其实都是把分数除法转化成分数乘法来算,具体是怎么转化的?
【设计意图:心理学研究证明,当将一个知识寓于完整的系统之中时,更易于学习者去理解记忆、去把握运用。因此,及时地将分数除以整数、整数除以分数和分数除以分数的计算方法归纳成一个有机的整体,更有助于学生的理解和掌握。对于学生而言,这是一种思维上的提升,越是简洁的东西,越是具有普遍适应性。】
三、 练习巩固,掌握算法。
1.基础练习
现在你会计算分数除以分数了吗?
检验一下 ÷ ÷
大家在练习本上计算,你们都是怎么算的?叫几个同学展示方法。
2.这些算式都缺少了一部分,能填完整吗?
÷=( )( )
÷( )=×
÷=( )×
÷( )=×( )
这两空所填的数有什么关系?如果第一空填a,第二空填什么?
想一想 这个a可以表示所有的数吗?为什么?看来,我们刚刚总结的计算方法里,还需强调一下(0除外)这个要求。
3.总结提升,探索规律。
我们再来算几道题。(逐题出示,学生计算后直接报结果)将计算过程写在练习本上。
出示÷3=,÷=,÷2=比一比他们的商与被除数,你有什么发现?生:商都比被除数小。你能再举几个商比被除数小的例子吗?(举例并计算)师:这些算式中,是哪一个数影响着商的大小(除数),什么情况下,商会小于被除数?(当除数大于1时,商小于被除数)什么情况下,商会等于被除数?(当除数等于1时,商等于被除数;)什么情况下,商又会大于被除数呢?(当除数小于1时,商大于被除数。)(举例说明)
需要注意的是这里的被除数和除数都不为0 。
【设计意图:此内容的安排,已经不满足于简单的方法运用这一层次,而是引导学生建立一种宏观视野,在熟练运用计算方法时,还应注意到结果的变化是有缘由的,也就是一种更高的系统化。】
四、 总结全课。
回顾整节课,我们一起学习了不少内容,看,老师在黑板上写下这么多的板书,你最想留下的是什么? 为什么?
板书设计
转化
分数除法——分数乘法
分数除以整数
学生列式
整数除以分数
学生列式
分数除以分数
÷ = × =3
甲数÷ 乙数 = 甲数× 乙数的倒数
(0除外)
