第3章 代数式单元测试重点题型精选(冀教版含解析)
文档属性
| 名称 | 第3章 代数式单元测试重点题型精选(冀教版含解析) |  | |
| 格式 | rar | ||
| 文件大小 | 214.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 21:51:13 | ||
图片预览



文档简介
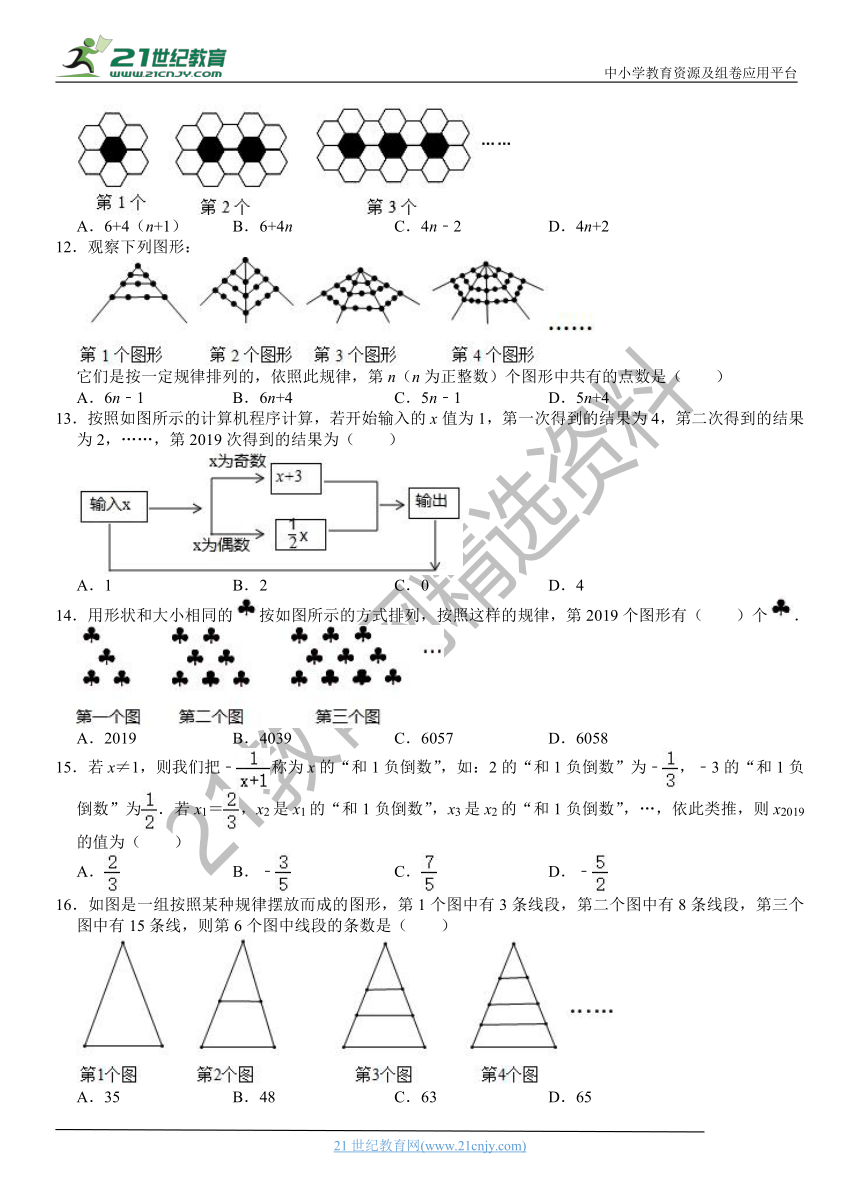
代数式
单元测试重点题型精选
一、选择题(共16小题)
1.下列各式最符合代数式书写规范的是( )
A.3a
B.
C.3x﹣1个
D.a×3
2.引进字母,用适当的代数式表示不正确的是( )
A.“除以7余3的数字”可表示为7a+3
B.奇数可表示为2n﹣1
C.“a与b两数的平方和减去它们积的两倍”可表示为(a+b)2﹣2ab
D.“底面半径为r,高为h的圆锥的体积”可表示为
3.若2019×14=m,则下列代数式表示2019×15的是( )
A.m+1
B.2019m+2019
C.m+15
D.m+2019
4.已知a2+2a=1,则代数式1﹣2(a2+2a)的值为( )
A.0
B.1
C.﹣1
D.﹣2
5.设某数为m,则代数式表示( )
A.某数的3倍的平方减去5除以2
B.某数平方的3倍与5的差的一半
C.某数的3倍减5的一半
D.某数与5的差的3倍除以2
6.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是( )
A.110
B.158
C.168
D.178
7.某企业今年9月份产值为m万元,10月份比9月份减少了5%,11月份比10月份增加了10%,则11月份的产值是( )
A.(m﹣5%)(m+10%)万元
B.(1﹣5%)(1+10%)m
万元
C.(m﹣5%+10%)万元
D.(1﹣5%+10%)m
万元
8.当x=3,y=2时,代数式的值是( )
A.
B.2
C.0
D.3
9.观察下列各数:,它们是按一定规律排列的,则第n个数是( )
A.
B.
C.
D.
10.如图为O、A、B、C四点在数轴上的位置图,其中O为原点,且AC=1,OA=OB,若点C所表示的数为x,则点B所表示的数为( )
A.﹣(x+1)
B.﹣(x﹣1)
C.x+1
D.x﹣1
11.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是由第1个图案经过平移而得,那么第n个图案中有白色六边形地面砖( )块.
A.6+4(n+1)
B.6+4n
C.4n﹣2
D.4n+2
12.观察下列图形:
它们是按一定规律排列的,依照此规律,第n(n为正整数)个图形中共有的点数是( )
A.6n﹣1
B.6n+4
C.5n﹣1
D.5n+4
13.按照如图所示的计算机程序计算,若开始输入的x值为1,第一次得到的结果为4,第二次得到的结果为2,……,第2019次得到的结果为( )
A.1
B.2
C.0
D.4
14.用形状和大小相同的按如图所示的方式排列,按照这样的规律,第2019个图形有( )个.
A.2019
B.4039
C.6057
D.6058
15.若x≠1,则我们把﹣称为x的“和1负倒数”,如:2的“和1负倒数”为﹣,﹣3的“和1负倒数”为.若x1=,x2是x1的“和1负倒数”,x3是x2的“和1负倒数”,…,依此类推,则x2019的值为( )
A.
B.﹣
C.
D.﹣
16.如图是一组按照某种规律摆放而成的图形,第1个图中有3条线段,第二个图中有8条线段,第三个图中有15条线,则第6个图中线段的条数是( )
A.35
B.48
C.63
D.65
二、填空题(共3小题)
17.已知整式x2﹣2x+6的值为,则﹣2x2+4x﹣12的值为
.
18.给定一列按规律排列的数:,1,,,…,根据前4个数的规律,第2020个数是
.
19.如图是由火柴棒搭成的几何图案,则第4个图案中有
根火柴棒;第n个图案中比第n﹣1个图案多
根火柴棒(用含n的代数式表示).
三、解答题(共7小题)
20.如图,是一所住宅的建筑平面图(图中长度单位:m).
(1)用式子表示这所住宅的建筑面积;
(2)若a=4,b=6,求出这所住宅的建筑面积.
21.某地出租车的收费标准如下:3千米以内(包括3千米)为起步价收费10元,3千米以后每千米收费2.4元.
(1)小明乘出租车行驶了2.3千米,他应付车费
元;
(2)小亮乘出租车行驶了7千米,他应付车费
元;
(3)小朋乘出租车去x千米(x>3)外的姥姥家,那么她要准备多少钱才够乘坐出租车?(用含x的代数式表示)
22.用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形1+3+5=9个小正方形;
第(5)个图形
个小正方形(直接写出结果);
…
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n﹣1)=
(用含n的代数式表示);
(2)请根据你的发现计算:①1+3+5+7+…+99=
;
②101+103+105+…+199=
.
23.观察下面三行数
﹣3,9,﹣27,81…①
1,﹣3,9,﹣27…②
﹣2,10,﹣26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③行的2019个数,求x+6y+z的值.
24.观察下列各式:﹣1×=﹣1+,﹣=﹣,﹣=﹣
(1)猜想:﹣×=
(写成和的形式)
(2)你发现的规律是:﹣×=
;(n为正整数)
(3)用规律计算:(﹣1×)+(﹣)+(﹣)+…+(﹣×)+(﹣×).
25.一种蔬菜x千克,不加工直接出售每千克可卖y元;如果经过加工重量减少了15%,价格增加了40%,问:
(1)x千克这种蔬菜加工后可卖多少钱?
(2)如果这种蔬菜1000千克,不加工直接出售每千克可卖1.50元,问加工后原1000千克这种蔬菜可卖多少钱?比加工前多卖多少钱?
26.某服装厂生产一种西装和领带,西装每套定价400元,领带每条定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案:
方案①:买一套西装送一条领带;
方案②:西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)若该客户按方案①购买,需付款
元(用含x的代数式表示);
若该客户按方案②购买,需付款
元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法并计算出此种方案的付款金额.
试题解析
1.解:A、正确的书写格式是,不符合题意;
B、正确,符合题意;
C、正确的书写格式是(3x﹣1)个,不符合题意;
D、正确的书写格式是3a,不符合题意.
故选:B.
2.解:A、“除以7余3的数字”可表示为7a+3,故正确;
B、奇数可表示为2n﹣1,故正确;
C、“a与b两数的平方和减去它们积的两倍”可表示为a2+b2﹣2ab,故错误;
D、底面半径为r,高为h的圆锥的体积”可表示为,故正确;
故选:C.
解:∵2019×14=m,
∴2019×15=2019×(14+1)=2019×14+2019=m+2019.
故选:D.
4.解:因为a2+2a=1,
所以1﹣2(a2+2a)
=1﹣2×1
=1﹣2
=﹣1.
故选:C.
5.解:∵设某数为m,代数式表示:某数平方的3倍与5的差的一半.
故选:B.
6.解:根据排列规律,10下面的数是12,10右面的数是14,
∵8=2×4﹣0,22=4×6﹣2,44=6×8﹣4,
∴m=12×14﹣10=158.
故选:B.
7.解:∵某企业今年9月份产值为m万元,10月份比9月份减少了5%,
∴该企业今年10月份产值为(1﹣5%)m万元,
又∵11月份比10月份增加了10%,
∴该企业今年11月份产值为(1﹣5%)(1+10%)m万元.
故选:B.
8.解:==
9.解:第n个数是.
故选:A.
10.解:∵AC=1,点C所表示的数为x,
∴点A表示的数为x﹣1,
∵O为原点,OA=OB,
∴点B所表示的数为﹣(x﹣1),
故选:B.
11.解:∵第一个图案中,有白色的是6个,后边是依次多4个.
∴第n个图案中,是6+4(n﹣1)=4n+2.
故选:D.
12.解:设第n个图形共有an个点(n为正整数),
观察图形,可知:a1=10=6+4,a2=16=6×2+4,a3=22=6×3+4,a4=28=6×4+4,…,
∴an=6n+4(n为正整数).
故选:B.
13.解:根据计算机程序可知:
开始输入的x值为1,
第一次得到的结果为4,
第二次得到的结果为2,
第三次得到的结果为1,
第四次得到的结果为4,
……,
发现规律:三次一循环结果为4、2、1,
2019÷3=693.
第2019次得到的结果为:1.
故选:A.
14.解:观察图形的变化可知:
第1个图形有(3×1+1=4)个;
第2个图形有(3×2+1=7)个;
第3个图形有(3×3+1=10)个;
…
发现规律:
第n个图形有(3n+1)个.
第2019个图形有(3×2019+1=6058)个.
故选:D.
15.解:∵x1=,
∴x2=﹣=﹣,
x3=﹣=﹣,
x4=﹣=,
……
∴此数列每3个数为一周期循环,
∵2019÷3=673,
∴x2019=x3=﹣,
故选:D.
16.解:由图可得,
第1个图形中有:3条线段,
第2个图形中有:3+3+2=3×2+2×1=8条线段,
第3个图形中有:3+3+3+2+2+2=3×3+2×3=15条线段,
第4个图形中有:3+3+3+3+2+2+2+2+2+2=3×4+2×6=24条线段,
…,
则第n个图形中有:[(n+1)2﹣1]条线段,
∴当n=6时,[(n+1)2﹣1]=[(6+1)2﹣1]=48,
故选:B.
17.解:∵x2﹣2x+6=,
∴x2﹣2x=﹣,
则原式=﹣2(x2﹣2x)﹣12
=﹣2×(﹣)﹣12
=﹣12
=﹣.
故答案为:﹣.
18.解:观察这列数发现,奇数项是负数,偶数项是正数;分子分别为3,5,7,9,…;分子分别为12+1,22+1,32+1,…,
∴该列数的第n项是(﹣1)n,
∴第2020个数是=,
故答案为.
19.解:∵第1个图案中有火柴棒根数为:4=1×2×2;
第2个图案中有火柴棒根数为:12=2×3×2;
第3个图案中有火柴棒根数为:24=3×4×2;
∴第4个图案中有火柴棒根数为4×5×2=40;
…
∴第n﹣1个图案中有火柴棒根数为:2n(n﹣1);
第n个图案中有火柴棒根数为:2n(n+1);
第n个图案中比第n﹣1个图案多4n根火柴棒.
故答案为:40,4n.
20.解:(1)这所宅子的建筑面积是:
S=2a?(3+b)+5×4+5a
=11a+2ab+20
(2)当a=4,b=6时,
S=11×4+2×4×6+20
=112(m2)
∴这所宅子的建筑面积为112m2.
21.解:(1)由题意可得,
小明乘出租车行驶了2.3千米,他应付车费10元,
故答案为:10;
(2)由题意可得,
小亮乘出租车行驶了7千米,他应付车费:10+(7﹣3)×2.4=10+4×2.4=10+9.6=19.6(元),
故答案为:19.6;
(3)由题意可得,
10+(x﹣3)×2.4=2.4x+2.8,
即她要准备(2.4x+2.8)元才够乘坐出租车.
22.解:第(5)个图形1+3+5+7+9=25个小正方形,
故答案为:25;
(1)1+3+5+7+…+(2n﹣1)==n2,
故答案为:n2;
(2)①令2n﹣1=99,得n=50,
则:1+3+5+7+…+99=502,
故答案为:502;
②101+103+105+…+199
=(1+3+5+…+199)﹣(1+3+5+…+99)
=1002﹣502
=(100+50)(100﹣50)
=150×50
=7500,
故答案为:7500.
23.解:(1)①行数后一个数前一个数的﹣3倍;
(2)②的每一个数是第一行对应数的﹣倍;③的每一个数是第①行对应数加1;
(3)由(1)(2)可得x=(﹣3)2019,y=(﹣3)2019×(﹣3)﹣1=(﹣3)2018,z=(﹣3)2019+1,
∴x+6y+z=(﹣3)2019+6×(﹣3)2018+(﹣3)2019+1=1.
24.解:(1)由所给的已知发现乘积的等于和,
∴﹣×=﹣+,
故答案为﹣+;
(2)﹣×=﹣+,
故答案为﹣+;
(3)(﹣1×)+(﹣)+(﹣)+…+(﹣×)+(﹣×)=﹣1+﹣﹣﹣…﹣+=﹣1+=﹣.
25.解:(1)x千克这种蔬菜加工后重量为x(1﹣15%)千克,价格为y(1+40%)元.
x千克这种蔬菜加工后可卖x(1﹣15%)?y(1+40%)=1.19xy元.
(2)加工后可卖1.19×1000×1.5=1785元,1.19×1000×1.5﹣1000×1.5=285(元),比加工前多卖285元.
26.解:(1)按方案①购买,需付款:400×20+(x﹣20)×50
=(7000+50x)元;
按方案②购买,需付款:400×90%×20+50×90%×x
=(45x+7200)元
故答案为:(50x+7000);(45x+7200);
(2)当x=30时
方案①:50×30+7000=8500(元)
方案②:45×30+7200=8550(元)8500元<8550元
答:此时按方案①购买较为合算.
(3)用方案①买20套西装送20条领带,再用方案②买10条领带.
总价钱为20×400+10×50×90%=8450(元)<8500元,
所以可以.
单元测试重点题型精选
一、选择题(共16小题)
1.下列各式最符合代数式书写规范的是( )
A.3a
B.
C.3x﹣1个
D.a×3
2.引进字母,用适当的代数式表示不正确的是( )
A.“除以7余3的数字”可表示为7a+3
B.奇数可表示为2n﹣1
C.“a与b两数的平方和减去它们积的两倍”可表示为(a+b)2﹣2ab
D.“底面半径为r,高为h的圆锥的体积”可表示为
3.若2019×14=m,则下列代数式表示2019×15的是( )
A.m+1
B.2019m+2019
C.m+15
D.m+2019
4.已知a2+2a=1,则代数式1﹣2(a2+2a)的值为( )
A.0
B.1
C.﹣1
D.﹣2
5.设某数为m,则代数式表示( )
A.某数的3倍的平方减去5除以2
B.某数平方的3倍与5的差的一半
C.某数的3倍减5的一半
D.某数与5的差的3倍除以2
6.填在下面各正方形中的四个数之间都有相同的规律,根据这种规律,m的值应是( )
A.110
B.158
C.168
D.178
7.某企业今年9月份产值为m万元,10月份比9月份减少了5%,11月份比10月份增加了10%,则11月份的产值是( )
A.(m﹣5%)(m+10%)万元
B.(1﹣5%)(1+10%)m
万元
C.(m﹣5%+10%)万元
D.(1﹣5%+10%)m
万元
8.当x=3,y=2时,代数式的值是( )
A.
B.2
C.0
D.3
9.观察下列各数:,它们是按一定规律排列的,则第n个数是( )
A.
B.
C.
D.
10.如图为O、A、B、C四点在数轴上的位置图,其中O为原点,且AC=1,OA=OB,若点C所表示的数为x,则点B所表示的数为( )
A.﹣(x+1)
B.﹣(x﹣1)
C.x+1
D.x﹣1
11.如图所示,第1个图案是由黑白两种颜色的六边形地面砖组成的,第2个,第3个图案可以看成是由第1个图案经过平移而得,那么第n个图案中有白色六边形地面砖( )块.
A.6+4(n+1)
B.6+4n
C.4n﹣2
D.4n+2
12.观察下列图形:
它们是按一定规律排列的,依照此规律,第n(n为正整数)个图形中共有的点数是( )
A.6n﹣1
B.6n+4
C.5n﹣1
D.5n+4
13.按照如图所示的计算机程序计算,若开始输入的x值为1,第一次得到的结果为4,第二次得到的结果为2,……,第2019次得到的结果为( )
A.1
B.2
C.0
D.4
14.用形状和大小相同的按如图所示的方式排列,按照这样的规律,第2019个图形有( )个.
A.2019
B.4039
C.6057
D.6058
15.若x≠1,则我们把﹣称为x的“和1负倒数”,如:2的“和1负倒数”为﹣,﹣3的“和1负倒数”为.若x1=,x2是x1的“和1负倒数”,x3是x2的“和1负倒数”,…,依此类推,则x2019的值为( )
A.
B.﹣
C.
D.﹣
16.如图是一组按照某种规律摆放而成的图形,第1个图中有3条线段,第二个图中有8条线段,第三个图中有15条线,则第6个图中线段的条数是( )
A.35
B.48
C.63
D.65
二、填空题(共3小题)
17.已知整式x2﹣2x+6的值为,则﹣2x2+4x﹣12的值为
.
18.给定一列按规律排列的数:,1,,,…,根据前4个数的规律,第2020个数是
.
19.如图是由火柴棒搭成的几何图案,则第4个图案中有
根火柴棒;第n个图案中比第n﹣1个图案多
根火柴棒(用含n的代数式表示).
三、解答题(共7小题)
20.如图,是一所住宅的建筑平面图(图中长度单位:m).
(1)用式子表示这所住宅的建筑面积;
(2)若a=4,b=6,求出这所住宅的建筑面积.
21.某地出租车的收费标准如下:3千米以内(包括3千米)为起步价收费10元,3千米以后每千米收费2.4元.
(1)小明乘出租车行驶了2.3千米,他应付车费
元;
(2)小亮乘出租车行驶了7千米,他应付车费
元;
(3)小朋乘出租车去x千米(x>3)外的姥姥家,那么她要准备多少钱才够乘坐出租车?(用含x的代数式表示)
22.用同样大小的两种不同颜色的正方形纸片,按下图方式拼正方形.
第(1)个图形中有1个正方形;
第(2)个图形有1+3=4个小正方形;
第(3)个图形1+3+5=9个小正方形;
第(5)个图形
个小正方形(直接写出结果);
…
(1)根据上面的发现我们可以猜想:1+3+5+7+…+(2n﹣1)=
(用含n的代数式表示);
(2)请根据你的发现计算:①1+3+5+7+…+99=
;
②101+103+105+…+199=
.
23.观察下面三行数
﹣3,9,﹣27,81…①
1,﹣3,9,﹣27…②
﹣2,10,﹣26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③行的2019个数,求x+6y+z的值.
24.观察下列各式:﹣1×=﹣1+,﹣=﹣,﹣=﹣
(1)猜想:﹣×=
(写成和的形式)
(2)你发现的规律是:﹣×=
;(n为正整数)
(3)用规律计算:(﹣1×)+(﹣)+(﹣)+…+(﹣×)+(﹣×).
25.一种蔬菜x千克,不加工直接出售每千克可卖y元;如果经过加工重量减少了15%,价格增加了40%,问:
(1)x千克这种蔬菜加工后可卖多少钱?
(2)如果这种蔬菜1000千克,不加工直接出售每千克可卖1.50元,问加工后原1000千克这种蔬菜可卖多少钱?比加工前多卖多少钱?
26.某服装厂生产一种西装和领带,西装每套定价400元,领带每条定价50元.厂方在开展促销活动期间,向客户提供两种优惠方案:
方案①:买一套西装送一条领带;
方案②:西装和领带都按定价的90%付款.
现某客户要到该服装厂购买西装20套,领带x条(x>20).
(1)若该客户按方案①购买,需付款
元(用含x的代数式表示);
若该客户按方案②购买,需付款
元(用含x的代数式表示);
(2)若x=30,通过计算说明此时按哪种方案购买较为合算?
(3)若两种优惠方案可同时使用,当x=30时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法并计算出此种方案的付款金额.
试题解析
1.解:A、正确的书写格式是,不符合题意;
B、正确,符合题意;
C、正确的书写格式是(3x﹣1)个,不符合题意;
D、正确的书写格式是3a,不符合题意.
故选:B.
2.解:A、“除以7余3的数字”可表示为7a+3,故正确;
B、奇数可表示为2n﹣1,故正确;
C、“a与b两数的平方和减去它们积的两倍”可表示为a2+b2﹣2ab,故错误;
D、底面半径为r,高为h的圆锥的体积”可表示为,故正确;
故选:C.
解:∵2019×14=m,
∴2019×15=2019×(14+1)=2019×14+2019=m+2019.
故选:D.
4.解:因为a2+2a=1,
所以1﹣2(a2+2a)
=1﹣2×1
=1﹣2
=﹣1.
故选:C.
5.解:∵设某数为m,代数式表示:某数平方的3倍与5的差的一半.
故选:B.
6.解:根据排列规律,10下面的数是12,10右面的数是14,
∵8=2×4﹣0,22=4×6﹣2,44=6×8﹣4,
∴m=12×14﹣10=158.
故选:B.
7.解:∵某企业今年9月份产值为m万元,10月份比9月份减少了5%,
∴该企业今年10月份产值为(1﹣5%)m万元,
又∵11月份比10月份增加了10%,
∴该企业今年11月份产值为(1﹣5%)(1+10%)m万元.
故选:B.
8.解:==
9.解:第n个数是.
故选:A.
10.解:∵AC=1,点C所表示的数为x,
∴点A表示的数为x﹣1,
∵O为原点,OA=OB,
∴点B所表示的数为﹣(x﹣1),
故选:B.
11.解:∵第一个图案中,有白色的是6个,后边是依次多4个.
∴第n个图案中,是6+4(n﹣1)=4n+2.
故选:D.
12.解:设第n个图形共有an个点(n为正整数),
观察图形,可知:a1=10=6+4,a2=16=6×2+4,a3=22=6×3+4,a4=28=6×4+4,…,
∴an=6n+4(n为正整数).
故选:B.
13.解:根据计算机程序可知:
开始输入的x值为1,
第一次得到的结果为4,
第二次得到的结果为2,
第三次得到的结果为1,
第四次得到的结果为4,
……,
发现规律:三次一循环结果为4、2、1,
2019÷3=693.
第2019次得到的结果为:1.
故选:A.
14.解:观察图形的变化可知:
第1个图形有(3×1+1=4)个;
第2个图形有(3×2+1=7)个;
第3个图形有(3×3+1=10)个;
…
发现规律:
第n个图形有(3n+1)个.
第2019个图形有(3×2019+1=6058)个.
故选:D.
15.解:∵x1=,
∴x2=﹣=﹣,
x3=﹣=﹣,
x4=﹣=,
……
∴此数列每3个数为一周期循环,
∵2019÷3=673,
∴x2019=x3=﹣,
故选:D.
16.解:由图可得,
第1个图形中有:3条线段,
第2个图形中有:3+3+2=3×2+2×1=8条线段,
第3个图形中有:3+3+3+2+2+2=3×3+2×3=15条线段,
第4个图形中有:3+3+3+3+2+2+2+2+2+2=3×4+2×6=24条线段,
…,
则第n个图形中有:[(n+1)2﹣1]条线段,
∴当n=6时,[(n+1)2﹣1]=[(6+1)2﹣1]=48,
故选:B.
17.解:∵x2﹣2x+6=,
∴x2﹣2x=﹣,
则原式=﹣2(x2﹣2x)﹣12
=﹣2×(﹣)﹣12
=﹣12
=﹣.
故答案为:﹣.
18.解:观察这列数发现,奇数项是负数,偶数项是正数;分子分别为3,5,7,9,…;分子分别为12+1,22+1,32+1,…,
∴该列数的第n项是(﹣1)n,
∴第2020个数是=,
故答案为.
19.解:∵第1个图案中有火柴棒根数为:4=1×2×2;
第2个图案中有火柴棒根数为:12=2×3×2;
第3个图案中有火柴棒根数为:24=3×4×2;
∴第4个图案中有火柴棒根数为4×5×2=40;
…
∴第n﹣1个图案中有火柴棒根数为:2n(n﹣1);
第n个图案中有火柴棒根数为:2n(n+1);
第n个图案中比第n﹣1个图案多4n根火柴棒.
故答案为:40,4n.
20.解:(1)这所宅子的建筑面积是:
S=2a?(3+b)+5×4+5a
=11a+2ab+20
(2)当a=4,b=6时,
S=11×4+2×4×6+20
=112(m2)
∴这所宅子的建筑面积为112m2.
21.解:(1)由题意可得,
小明乘出租车行驶了2.3千米,他应付车费10元,
故答案为:10;
(2)由题意可得,
小亮乘出租车行驶了7千米,他应付车费:10+(7﹣3)×2.4=10+4×2.4=10+9.6=19.6(元),
故答案为:19.6;
(3)由题意可得,
10+(x﹣3)×2.4=2.4x+2.8,
即她要准备(2.4x+2.8)元才够乘坐出租车.
22.解:第(5)个图形1+3+5+7+9=25个小正方形,
故答案为:25;
(1)1+3+5+7+…+(2n﹣1)==n2,
故答案为:n2;
(2)①令2n﹣1=99,得n=50,
则:1+3+5+7+…+99=502,
故答案为:502;
②101+103+105+…+199
=(1+3+5+…+199)﹣(1+3+5+…+99)
=1002﹣502
=(100+50)(100﹣50)
=150×50
=7500,
故答案为:7500.
23.解:(1)①行数后一个数前一个数的﹣3倍;
(2)②的每一个数是第一行对应数的﹣倍;③的每一个数是第①行对应数加1;
(3)由(1)(2)可得x=(﹣3)2019,y=(﹣3)2019×(﹣3)﹣1=(﹣3)2018,z=(﹣3)2019+1,
∴x+6y+z=(﹣3)2019+6×(﹣3)2018+(﹣3)2019+1=1.
24.解:(1)由所给的已知发现乘积的等于和,
∴﹣×=﹣+,
故答案为﹣+;
(2)﹣×=﹣+,
故答案为﹣+;
(3)(﹣1×)+(﹣)+(﹣)+…+(﹣×)+(﹣×)=﹣1+﹣﹣﹣…﹣+=﹣1+=﹣.
25.解:(1)x千克这种蔬菜加工后重量为x(1﹣15%)千克,价格为y(1+40%)元.
x千克这种蔬菜加工后可卖x(1﹣15%)?y(1+40%)=1.19xy元.
(2)加工后可卖1.19×1000×1.5=1785元,1.19×1000×1.5﹣1000×1.5=285(元),比加工前多卖285元.
26.解:(1)按方案①购买,需付款:400×20+(x﹣20)×50
=(7000+50x)元;
按方案②购买,需付款:400×90%×20+50×90%×x
=(45x+7200)元
故答案为:(50x+7000);(45x+7200);
(2)当x=30时
方案①:50×30+7000=8500(元)
方案②:45×30+7200=8550(元)8500元<8550元
答:此时按方案①购买较为合算.
(3)用方案①买20套西装送20条领带,再用方案②买10条领带.
总价钱为20×400+10×50×90%=8450(元)<8500元,
所以可以.
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
