北师大版九年级上册1.3.1正方形的定义和性质课件(21张ppt)
文档属性
| 名称 | 北师大版九年级上册1.3.1正方形的定义和性质课件(21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
正方形的性质
1
19
(1)回忆并比较菱形与矩形的性质
矩形
边:
角:
对角线:
对边平行且相等.
四个角都是直角.
对角线平分且相等.
菱形
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
对角相等,邻角互补
角:
2
19
正方形
正方形
菱形
想一想:正方形是怎样的菱形?
+一个角是直角
3
19
想一想:正方形是怎样的矩形?
矩形
正方形
矩形
正方形
+邻边相等
折一折:给你一张矩形纸能把它折成一个正方形吗?
4
19
平行四边形
正方形
矩形
菱形
+一组邻边相等
+一组邻边相等
+一个内角是直角
+一个内角是直角
平行四边形
正方形
+一组邻边相等
+一内角是直角
类比归纳
定义:一组邻边相等,且有一个角是直角的平行四边形叫做正方形
5
19
菱形
矩形
平行四边形
正
方
形
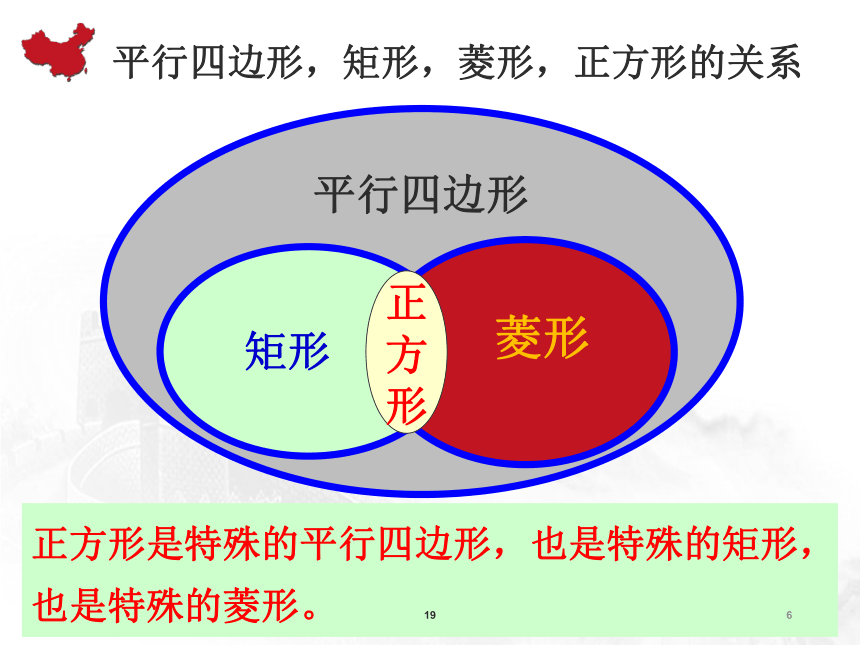
平行四边形,矩形,菱形,正方形的关系
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
6
19
正方形的性质=
菱形性质
矩形性质
知识梳理
7
19
对角线:相等
互相垂直平分
每条对角线平分一组对角
边:
对边平行
四边相等
角
:四个角都是直角
图形的对称性:既是轴对称图形,
又是中心对称图形.
=菱形性质
矩形性质
正方形的性质
8
19
√
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形(
)
快速反应
判断题:
(2)正方形一定是矩形.(
)
(3)正方形一定是菱形.(
)
(4)菱形一定是正方形.(
)
(5)矩形一定是正方形.(
)
(6)正方形、矩形、菱形都是平行四边形.
(
)
√
√
×
×
√
(7)正方形是轴对称图形,一共有2条对称轴(
)
×
9
19
正方形具有而矩形不一定具有的性质是(
)
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.
2.正方形具有而菱形不一定具有的性质(
)
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
选择题:
10
19
1.有一个内角是
的平行四边形是矩形。
2.有一组
相等的平行四边形是菱形。
3.下列性质中:①对角相等;②对边相等;③对角互补;④对角线相等;⑤对角线互相平分;⑥对角线互相垂直;⑦一条对角线平分一组对角,矩形具有而一般的平行四边形不具有的性质是
;菱形具有而一般的平行四边形不具有的性质是
。
4.下列图形中既是中心对称又是轴对称的是
(把序号填在横线上)①等边三角形,②平行四边形,③矩形,④线段,⑤菱形,⑥角。
直角
邻边
③④
⑥⑦
③④⑤
11
19
填空题
挑战自我
1.如图所示,在正方形ABCD中,已知AC=6,则正方形的面积为______
A
B
C
D
18
2.如图所示,在正方形ABCD中,AC
与BD相交于点O,AE=OA,则∠EOD=
_______.
D
A
B
C
E
O
(2)
22.5°
12
19
3.
13
19
4
变式:如右图,已知正方形ABCD,以AB为边向正方形外作等边三角形ABE,连结DE
、
CE,求∠DEC的度数。
14
19
A
B
D
C
F
E
5.如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC.
15
19
变式:正方形ABCD中,∠DAF=25°,AF交对角线BD于E,交CD于F,求∠
BEC的度数.
A
B
C
D
E
F
若∠FEC=30°则∠DAF=
16
19
6.如图所示,在平面直角坐标系中,正方形ABCD边长为1且AD与X轴重合,A点坐标为(1,0)则直线AC的表达式为_________
O
X
Y
A
D
C
B
(3)
y
=
x-1
17
19
对边平行且相等
每条对角线平分一组对角
对角线相等
对角线互相垂直
对角线互相平分
四个角都是直角
对角相等
四条边都相等
性质
正方形
菱形
矩形
平行四边形
图形
拓展延伸
对比归纳
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
18
19
通过本节课的学习,你有什么收获?
正方形
名称
特征
性
质
定
义
边
角
对角线
对称性
有一组邻边相等且有一个内角是直角的平行四边形叫做正方形
对边平行且相等,四条边相等
对角线相等且互相垂直平分
轴对称、中心对称图形,有4条对称轴
四个角都是直角
19
19
7.如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.
BE与DF之间有
怎样的关系?请说明理由.
拓展探究
D
F
C
E
A
B
F
F
F
F
F’
D’
(2)当线段DF平移到点F与点C重合时,DF是否仍与BE垂直相等?
M
20
19
(3)在正方形ABCD内部,若存在两条线段互相垂直(其端点均在正方形对边上),则这两条线段有何数量关系?
B
A
C
E
F
M
N
D
(4)在(3)基础上,若两条线段均过正方形ABCD的对称中心点O,此时,这两条线段有何关系?正方形被分成的四个区域有何关系?
D
A
B
C
O
F
E
N
M
21
19
正方形的性质
1
19
(1)回忆并比较菱形与矩形的性质
矩形
边:
角:
对角线:
对边平行且相等.
四个角都是直角.
对角线平分且相等.
菱形
边:
四条边相等
对角线:
互相垂直平分
分别平分两组对角
对角相等,邻角互补
角:
2
19
正方形
正方形
菱形
想一想:正方形是怎样的菱形?
+一个角是直角
3
19
想一想:正方形是怎样的矩形?
矩形
正方形
矩形
正方形
+邻边相等
折一折:给你一张矩形纸能把它折成一个正方形吗?
4
19
平行四边形
正方形
矩形
菱形
+一组邻边相等
+一组邻边相等
+一个内角是直角
+一个内角是直角
平行四边形
正方形
+一组邻边相等
+一内角是直角
类比归纳
定义:一组邻边相等,且有一个角是直角的平行四边形叫做正方形
5
19
菱形
矩形
平行四边形
正
方
形
平行四边形,矩形,菱形,正方形的关系
正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形。
6
19
正方形的性质=
菱形性质
矩形性质
知识梳理
7
19
对角线:相等
互相垂直平分
每条对角线平分一组对角
边:
对边平行
四边相等
角
:四个角都是直角
图形的对称性:既是轴对称图形,
又是中心对称图形.
=菱形性质
矩形性质
正方形的性质
8
19
√
(1)正方形的一条对角线把正方形分成两个全等的
等腰直角三角形(
)
快速反应
判断题:
(2)正方形一定是矩形.(
)
(3)正方形一定是菱形.(
)
(4)菱形一定是正方形.(
)
(5)矩形一定是正方形.(
)
(6)正方形、矩形、菱形都是平行四边形.
(
)
√
√
×
×
√
(7)正方形是轴对称图形,一共有2条对称轴(
)
×
9
19
正方形具有而矩形不一定具有的性质是(
)
A、四个角相等.
B、对角线互相垂直平分.
C、对角互补.
D、对角线相等.
2.正方形具有而菱形不一定具有的性质(
)
A、四条边相等.
B、对角线互相垂直平分.
C、对角线平分一组对角.
D、对角线相等.
B
D
选择题:
10
19
1.有一个内角是
的平行四边形是矩形。
2.有一组
相等的平行四边形是菱形。
3.下列性质中:①对角相等;②对边相等;③对角互补;④对角线相等;⑤对角线互相平分;⑥对角线互相垂直;⑦一条对角线平分一组对角,矩形具有而一般的平行四边形不具有的性质是
;菱形具有而一般的平行四边形不具有的性质是
。
4.下列图形中既是中心对称又是轴对称的是
(把序号填在横线上)①等边三角形,②平行四边形,③矩形,④线段,⑤菱形,⑥角。
直角
邻边
③④
⑥⑦
③④⑤
11
19
填空题
挑战自我
1.如图所示,在正方形ABCD中,已知AC=6,则正方形的面积为______
A
B
C
D
18
2.如图所示,在正方形ABCD中,AC
与BD相交于点O,AE=OA,则∠EOD=
_______.
D
A
B
C
E
O
(2)
22.5°
12
19
3.
13
19
4
变式:如右图,已知正方形ABCD,以AB为边向正方形外作等边三角形ABE,连结DE
、
CE,求∠DEC的度数。
14
19
A
B
D
C
F
E
5.如图,在正方形ABCD中,E在BC的延长线上,且CE=AC,AE交CD于F,则求∠AFC.
15
19
变式:正方形ABCD中,∠DAF=25°,AF交对角线BD于E,交CD于F,求∠
BEC的度数.
A
B
C
D
E
F
若∠FEC=30°则∠DAF=
16
19
6.如图所示,在平面直角坐标系中,正方形ABCD边长为1且AD与X轴重合,A点坐标为(1,0)则直线AC的表达式为_________
O
X
Y
A
D
C
B
(3)
y
=
x-1
17
19
对边平行且相等
每条对角线平分一组对角
对角线相等
对角线互相垂直
对角线互相平分
四个角都是直角
对角相等
四条边都相等
性质
正方形
菱形
矩形
平行四边形
图形
拓展延伸
对比归纳
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
√
18
19
通过本节课的学习,你有什么收获?
正方形
名称
特征
性
质
定
义
边
角
对角线
对称性
有一组邻边相等且有一个内角是直角的平行四边形叫做正方形
对边平行且相等,四条边相等
对角线相等且互相垂直平分
轴对称、中心对称图形,有4条对称轴
四个角都是直角
19
19
7.如图,在正方形ABCD中,E为CD上一点,F为BC边延长线上一点,且CE=CF.
BE与DF之间有
怎样的关系?请说明理由.
拓展探究
D
F
C
E
A
B
F
F
F
F
F’
D’
(2)当线段DF平移到点F与点C重合时,DF是否仍与BE垂直相等?
M
20
19
(3)在正方形ABCD内部,若存在两条线段互相垂直(其端点均在正方形对边上),则这两条线段有何数量关系?
B
A
C
E
F
M
N
D
(4)在(3)基础上,若两条线段均过正方形ABCD的对称中心点O,此时,这两条线段有何关系?正方形被分成的四个区域有何关系?
D
A
B
C
O
F
E
N
M
21
19
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
