沪科版九年级上册22.2.4相似三角形的判定课件(16张ppt)
文档属性
| 名称 | 沪科版九年级上册22.2.4相似三角形的判定课件(16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 635.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 10:26:52 | ||
图片预览






文档简介
(共16张PPT)
22.2.4相似三角形的判定(四)
学习目标
【学习目标】
1.经历三角形相似的判定定理3的探索及证明过程.
2.能应用定理3判定两个三角形相似,解决相关问题.
【学习重点】
三角形相似的判定定理3及应用.
【学习难点】
三角形相似的判定定理3的证明.
情景导入
旧知回顾:
1.简述全等三角形的判定定理“SSS”内容.
三边对应相等的两个三角形全等.
2.我们已经学过相似三角形的哪些判定方法?
(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
(2)两边对应成比例且夹角相等,两三角形相似.
(3)两角对应相等,两三角形相似.
知识模块一
三角形相似的判定定理3的证明
三角形相似的判定定理3是什么?如何证明?
判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.(简称:三边成比例的两个三角形相似)
自学互研
探究:已知:如图,△A′B′C′和△ABC中,
=
=
.
求证:△ABC∽△A′B′C′.
证明:在A′B′上截A′D=AB,
过D作DE∥B′C′交A′C′于E.∵DE∥B′C′,
∴△A′DE∽△A′B′C′,
∴
=
=
.
又∵
=
=
,
∴A′D=AB,AC=A′E,DE=BC,
∴△ABC≌△A′DE(SSS),∵△A′DE∽△A′B′C′,∴△ABC∽△A′B′C′.
范例
已知ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2cm,3cm B.4cm,5cm
C.5cm,6cm D.6cm,7cm
C
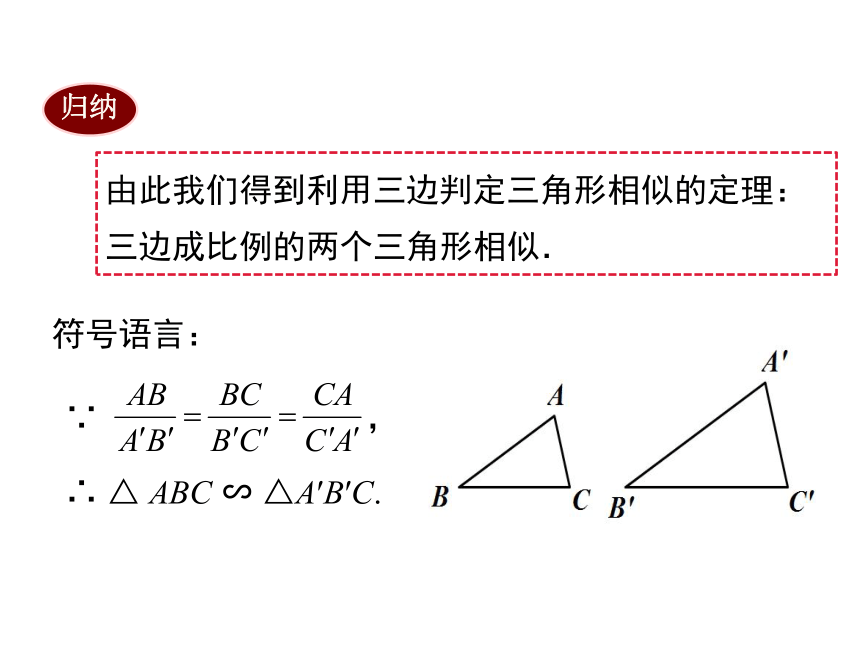
由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
∵
,
∴
△
ABC
∽
△A′B′C.
符号语言:
归纳
知识模块二
三角形相似的判定定理3的应用
例:如图,
方格网的小方格是边长为1的正方形,
△ABC与△
A′B′C′的顶点都在格点上,△
ABC与
△A′B′C′相似吗?为什么?
C
B
A
A′
B′
C′
解:△
ABC与△
A′B′C′的顶点都在格点上,根据勾股定理,得
∴
△
ABC与△
A′B′C′相似.
范例
1:如图,已知
=
=
,证明:∠BAD=∠CAE.
【分析】欲证∠BAD=∠CAE,可先证明△ABC∽△ADE,推出∠BAC=∠DAE,进而得出结论,而由已知条件中三边对应成比例,知必有两三角形相似.
证明:∵
=
=
.
∴△ABC∽△ADE,∴∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
2:如图,点D、E分别是等边三角形ABC的BC、AC边上的点,且BD=CE,AD与BE相交于点F.
(1)证明:△ABD≌△BCE;
(2)BD2=AD·DF吗?为什么?
证明:(1)△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
又∵BD=CE,∴△ABD≌△BCE(SAS).
(2)∵△ABD≌△BCE,∴∠BAD=∠CBE,
又∵∠ADB=∠BDF,∴△ABD∽△BFD,
∴
=
,∴BD2=DF·AD.
检测反馈
1.如图,在?ABCD中,AB=10,AD=6,E是AD的中点,在边AB上取点F,当BF=_______时,△CBF与△CDE相似.
1.8
2.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
,A
,B
,C
,D
B
3.如图,等腰直角三角形ABC中,顶点为C,∠MCN=45°,试说明△BCM∽△ANC.
解:∵∠A=∠B=45°,
又∵∠ANC=∠NCB+45°,
∠BCM=∠NCB+45°,
∴∠ANC=∠BCM,∴△BCM∽△ANC.
4.已知,如图,D为△ABC内一点,连接BD、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD.求证:△DBE∽△ABC.
证明:∵∠CBE=∠ABD,∠BCE=∠BAD,∴△ABD∽△CBE,∴
=
.
∵∠ABD+∠DBC=∠CBE+∠DBC,
即∠ABC=∠DBE,∴△ABC∽△DBE.
5.
如图,△ABC中,点
D,E,F
分别是
AB,BC,CA
的中点,求证:△ABC∽△EFD.
∴
△ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,
CA的中点,
∴
∴
三边成比例的两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
课堂小结
22.2.4相似三角形的判定(四)
学习目标
【学习目标】
1.经历三角形相似的判定定理3的探索及证明过程.
2.能应用定理3判定两个三角形相似,解决相关问题.
【学习重点】
三角形相似的判定定理3及应用.
【学习难点】
三角形相似的判定定理3的证明.
情景导入
旧知回顾:
1.简述全等三角形的判定定理“SSS”内容.
三边对应相等的两个三角形全等.
2.我们已经学过相似三角形的哪些判定方法?
(1)平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似.
(2)两边对应成比例且夹角相等,两三角形相似.
(3)两角对应相等,两三角形相似.
知识模块一
三角形相似的判定定理3的证明
三角形相似的判定定理3是什么?如何证明?
判定定理3:如果一个三角形的三条边与另一个三角形的三条边对应成比例,那么这两个三角形相似.(简称:三边成比例的两个三角形相似)
自学互研
探究:已知:如图,△A′B′C′和△ABC中,
=
=
.
求证:△ABC∽△A′B′C′.
证明:在A′B′上截A′D=AB,
过D作DE∥B′C′交A′C′于E.∵DE∥B′C′,
∴△A′DE∽△A′B′C′,
∴
=
=
.
又∵
=
=
,
∴A′D=AB,AC=A′E,DE=BC,
∴△ABC≌△A′DE(SSS),∵△A′DE∽△A′B′C′,∴△ABC∽△A′B′C′.
范例
已知ABC的三边长分别为6cm,7.5cm,9cm,△DEF的一边长为4cm,当△DEF的另两边长是下列哪一组时,这两个三角形相似( )
A.2cm,3cm B.4cm,5cm
C.5cm,6cm D.6cm,7cm
C
由此我们得到利用三边判定三角形相似的定理:
三边成比例的两个三角形相似.
∵
,
∴
△
ABC
∽
△A′B′C.
符号语言:
归纳
知识模块二
三角形相似的判定定理3的应用
例:如图,
方格网的小方格是边长为1的正方形,
△ABC与△
A′B′C′的顶点都在格点上,△
ABC与
△A′B′C′相似吗?为什么?
C
B
A
A′
B′
C′
解:△
ABC与△
A′B′C′的顶点都在格点上,根据勾股定理,得
∴
△
ABC与△
A′B′C′相似.
范例
1:如图,已知
=
=
,证明:∠BAD=∠CAE.
【分析】欲证∠BAD=∠CAE,可先证明△ABC∽△ADE,推出∠BAC=∠DAE,进而得出结论,而由已知条件中三边对应成比例,知必有两三角形相似.
证明:∵
=
=
.
∴△ABC∽△ADE,∴∠BAC=∠DAE,∴∠BAC-∠DAC=∠DAE-∠DAC,即∠BAD=∠CAE.
2:如图,点D、E分别是等边三角形ABC的BC、AC边上的点,且BD=CE,AD与BE相交于点F.
(1)证明:△ABD≌△BCE;
(2)BD2=AD·DF吗?为什么?
证明:(1)△ABC是等边三角形,
∴AB=BC,∠ABD=∠C=60°,
又∵BD=CE,∴△ABD≌△BCE(SAS).
(2)∵△ABD≌△BCE,∴∠BAD=∠CBE,
又∵∠ADB=∠BDF,∴△ABD∽△BFD,
∴
=
,∴BD2=DF·AD.
检测反馈
1.如图,在?ABCD中,AB=10,AD=6,E是AD的中点,在边AB上取点F,当BF=_______时,△CBF与△CDE相似.
1.8
2.如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( )
,A
,B
,C
,D
B
3.如图,等腰直角三角形ABC中,顶点为C,∠MCN=45°,试说明△BCM∽△ANC.
解:∵∠A=∠B=45°,
又∵∠ANC=∠NCB+45°,
∠BCM=∠NCB+45°,
∴∠ANC=∠BCM,∴△BCM∽△ANC.
4.已知,如图,D为△ABC内一点,连接BD、AD,以BC为边在△ABC外作∠CBE=∠ABD,∠BCE=∠BAD.求证:△DBE∽△ABC.
证明:∵∠CBE=∠ABD,∠BCE=∠BAD,∴△ABD∽△CBE,∴
=
.
∵∠ABD+∠DBC=∠CBE+∠DBC,
即∠ABC=∠DBE,∴△ABC∽△DBE.
5.
如图,△ABC中,点
D,E,F
分别是
AB,BC,CA
的中点,求证:△ABC∽△EFD.
∴
△ABC∽△EFD.
证明:∵△ABC中,点D,E,F分别是AB,BC,
CA的中点,
∴
∴
三边成比例的两个三角形相似
利用三边判定两个三角形相似
相似三角形的判定定理的运用
课堂小结
