鲁教版 (五四版)七年级上册《第5章 位置与坐标》 单元测试卷 word解析版
文档属性
| 名称 | 鲁教版 (五四版)七年级上册《第5章 位置与坐标》 单元测试卷 word解析版 |  | |
| 格式 | zip | ||
| 文件大小 | 178.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 20:58:19 | ||
图片预览


文档简介
第5章
位置与坐标
一、选择题(每小题3分,共24分)
1.已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )
A.(4,0)
B.(0,4)
C.(﹣4,0)
D.(0,﹣4)
2.在平面直角坐标系中,将点A(3,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(1,1)
B.(3,1)
C.(1,2)
D.(1,﹣5)
3.在平面直角坐标系中,已知点A(﹣4,3)与点B关于原点对称,则点B的坐标为( )
A.(﹣4,﹣3)
B.(4,3)
C.(4,﹣3)
D.(﹣4,3)
4.在平面直角坐标系中,点P(m,2m﹣2),则点P不可能在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.如图,若在象棋盘上建立平面直角坐标系xOy,使“帅”的坐标为(﹣1,﹣2)“马”的坐标为(2,﹣2),则“兵”的坐标为( )
A.(﹣3,1)
B.(﹣2,1)
C.(﹣3,0)
D.(﹣2,3)
6.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°)
B.Q(3,﹣120°)
C.Q(3,600°)
D.Q(3,﹣500°)
7.已知点P(a﹣3,2﹣a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
8.在平面直角坐标系中,若点P(m﹣2,m+1)在第二象限,则m的取值范围是( )
A.m<﹣1
B.m>2
C.﹣1<m<2
D.m>﹣1
二、填空题(每小题4分,共24分)
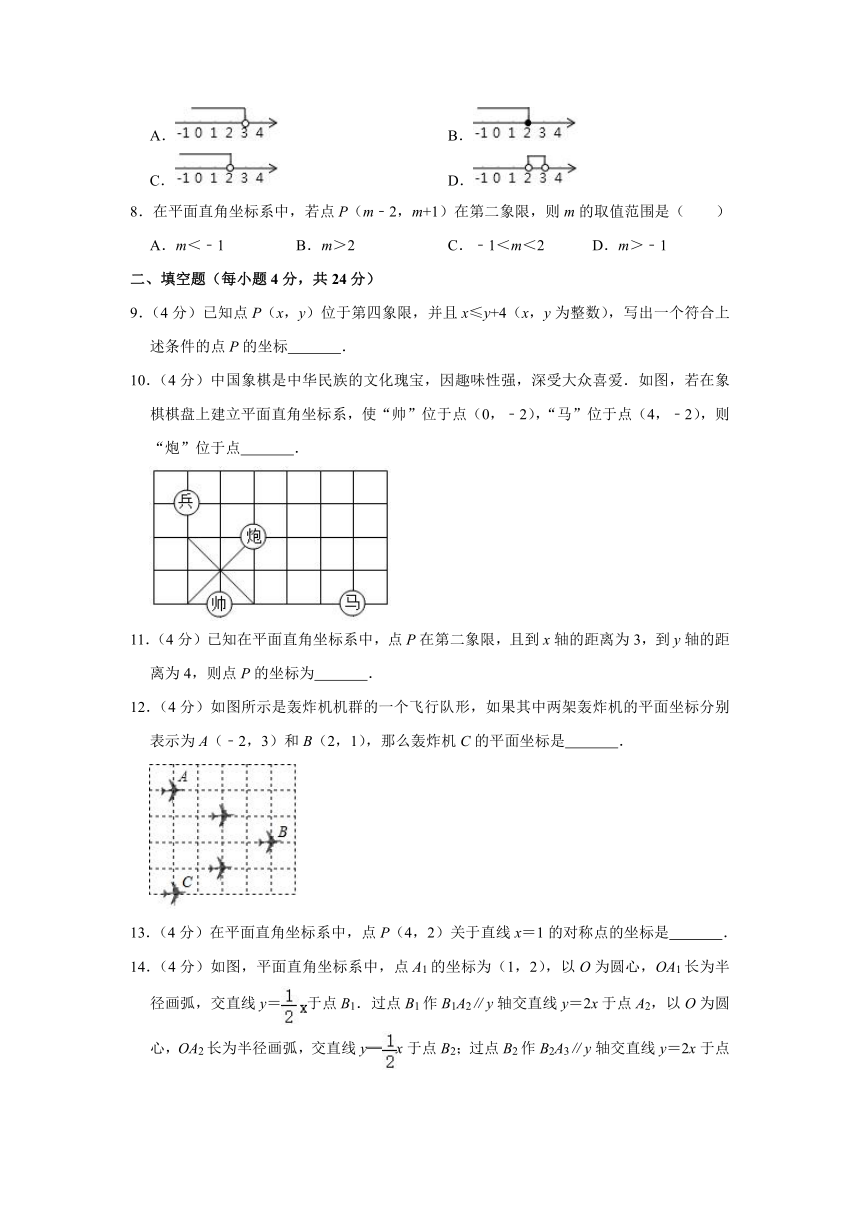
9.(4分)已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标
.
10.(4分)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,﹣2),“马”位于点(4,﹣2),则“炮”位于点
.
11.(4分)已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为
.
12.(4分)如图所示是轰炸机机群的一个飞行队形,如果其中两架轰炸机的平面坐标分别表示为A(﹣2,3)和B(2,1),那么轰炸机C的平面坐标是
.
13.(4分)在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是
.
14.(4分)如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y=于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=x于点B3;……按如此规律进行下去,点B2020的坐标为
.
三、解答题(15-18每题10分,19题12分,共52分)
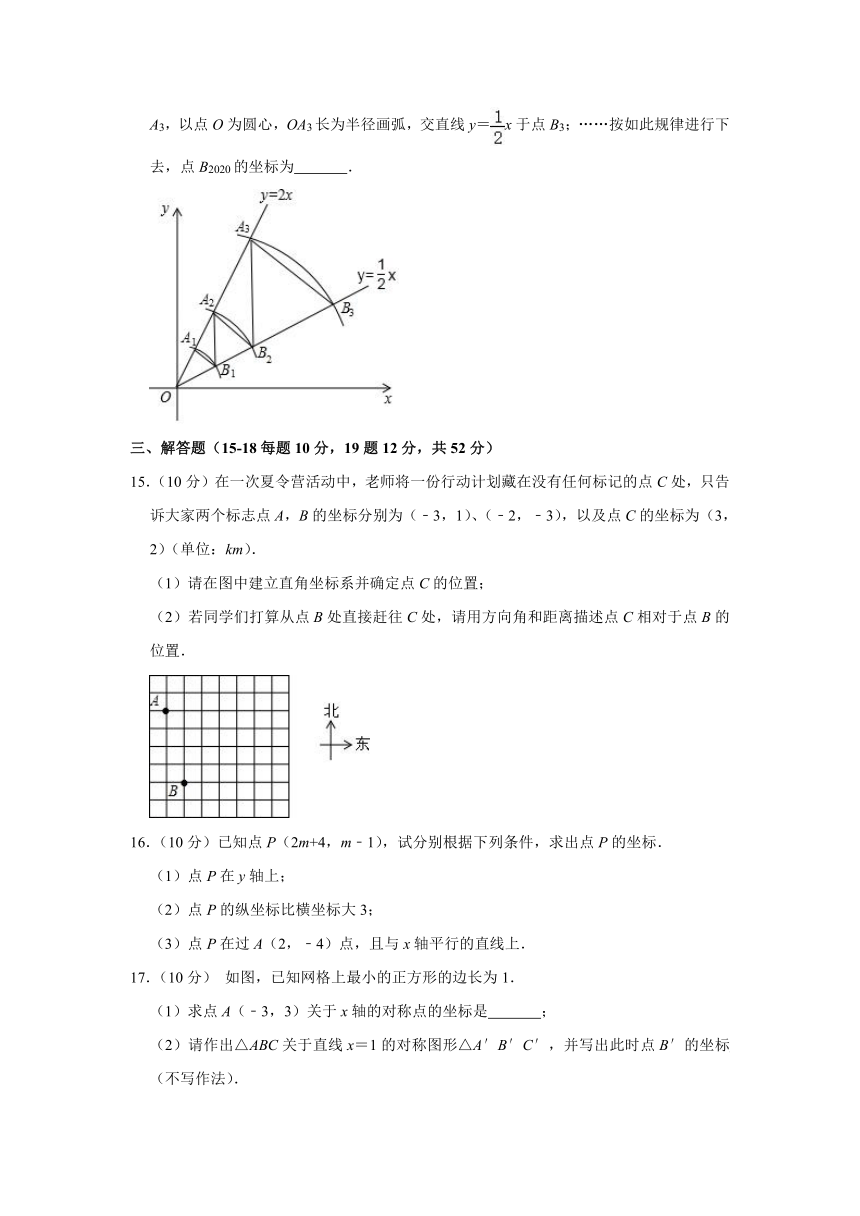
15.(10分)在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(﹣3,1)、(﹣2,﹣3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立直角坐标系并确定点C的位置;
(2)若同学们打算从点B处直接赶往C处,请用方向角和距离描述点C相对于点B的位置.
16.(10分)已知点P(2m+4,m﹣1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过A(2,﹣4)点,且与x轴平行的直线上.
17.(10分)
如图,已知网格上最小的正方形的边长为1.
(1)求点A(﹣3,3)关于x轴的对称点的坐标是
;
(2)请作出△ABC关于直线x=1的对称图形△A′B′C′,并写出此时点B′的坐标
(不写作法).
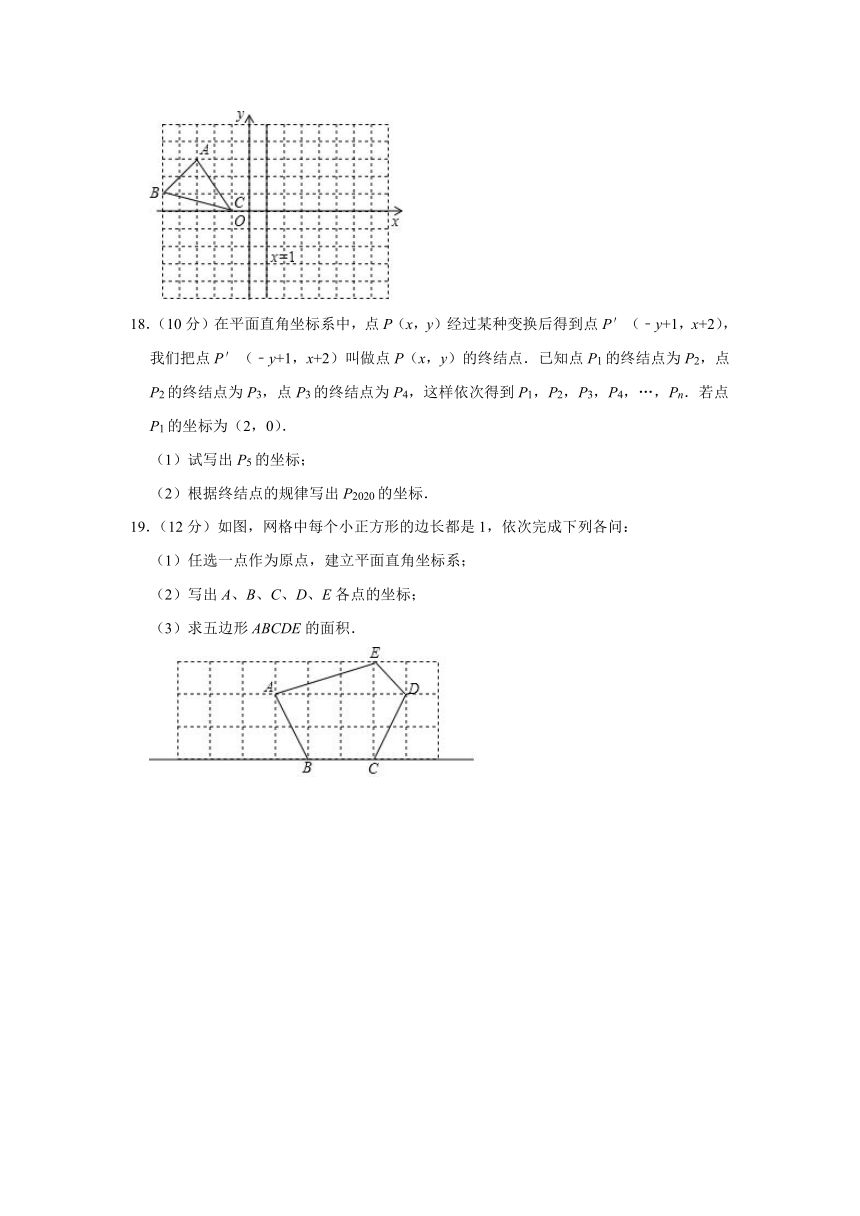
18.(10分)在平面直角坐标系中,点P(x,y)经过某种变换后得到点P′(﹣y+1,x+2),我们把点P′(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1,P2,P3,P4,…,Pn.若点P1的坐标为(2,0).
(1)试写出P5的坐标;
(2)根据终结点的规律写出P2020的坐标.
19.(12分)如图,网格中每个小正方形的边长都是1,依次完成下列各问:
(1)任选一点作为原点,建立平面直角坐标系;
(2)写出A、B、C、D、E各点的坐标;
(3)求五边形ABCDE的面积.
参考答案与试题解析
一、选择题(每小题3分,共24分)
1.已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )
A.(4,0)
B.(0,4)
C.(﹣4,0)
D.(0,﹣4)
【分析】直接利用关于x轴上点的坐标特点得出m的值,进而得出答案.
【解答】解:∵点P(m+2,2m﹣4)在x轴上,
∴2m﹣4=0,
解得:m=2,
∴m+2=4,
则点P的坐标是:(4,0).
故选:A.
2.在平面直角坐标系中,将点A(3,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(1,1)
B.(3,1)
C.(1,2)
D.(1,﹣5)
【分析】根据向左平移横坐标减,向上平移纵坐标加求解即可.
【解答】解:将点A(3,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A'的坐标为(3﹣2,﹣2+3),即(1,1),
故选:A.
3.在平面直角坐标系中,已知点A(﹣4,3)与点B关于原点对称,则点B的坐标为( )
A.(﹣4,﹣3)
B.(4,3)
C.(4,﹣3)
D.(﹣4,3)
【分析】根据关于原点的对称点,横、纵坐标都变成相反数解答.
【解答】解:∵点A(﹣4,3),点A与点B关于原点对称,
∴点B(4,﹣3).
故选:C.
4.在平面直角坐标系中,点P(m,2m﹣2),则点P不可能在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【分析】依据不同象限内点的坐标的符号特征分四种情况讨论,即可得到点P可能的位置.
【解答】解:当m>1时,2m﹣2>0,故点P可能在第一象限;
当m<0时,2m﹣2<0,故点P不可能在第二象限;
当m<0时,2m﹣2<0,故点P可能在第三象限;
当0<m<1时,2m﹣2<0,故点P可能在第四象限;
故选:B.
5.如图,若在象棋盘上建立平面直角坐标系xOy,使“帅”的坐标为(﹣1,﹣2)“马”的坐标为(2,﹣2),则“兵”的坐标为( )
A.(﹣3,1)
B.(﹣2,1)
C.(﹣3,0)
D.(﹣2,3)
【分析】直接利用“帅”位于点(﹣1,﹣2),可得原点的位置,进而得出“兵”的坐标.
【解答】解:如图所示:可得“炮”是原点,
则“兵”位于点:(﹣3,1).
故选:A.
6.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°)
B.Q(3,﹣120°)
C.Q(3,600°)
D.Q(3,﹣500°)
【分析】根据中心对称的性质解答即可.
【解答】解:∵P(3,60°)或P(3,﹣300°)或P(3,420°),
由点P关于点O成中心对称的点Q可得:点Q的极坐标为(3,240°),(3,﹣120°),(3,600°),
故选:D.
7.已知点P(a﹣3,2﹣a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
【分析】直接利用关于原点对称点的性质得出关于a的不等式组进而求出答案.
【解答】解:∵点P(a﹣3,2﹣a)关于原点对称的点在第四象限,
∴点P(a﹣3,2﹣a)在第二象限,
∴,
解得:a<2.
则a的取值范围在数轴上表示正确的是:.
故选:C.
8.在平面直角坐标系中,若点P(m﹣2,m+1)在第二象限,则m的取值范围是( )
A.m<﹣1
B.m>2
C.﹣1<m<2
D.m>﹣1
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组求解即可.
【解答】解:∵点P(m﹣2,m+1)在第二象限,
∴,
解得﹣1<m<2.
故选:C.
二、填空题(每小题4分,共24分)
9.(4分)已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标 (1,﹣2)(答案不唯一) .
【分析】直接利用第四象限内点的坐标特点得出x,y的取值范围,进而得出答案.
【解答】解:∵点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),
∴x>0,y<0,
∴当x=1时,1≤y+4,
解得:0>y≥﹣3,
∴y可以为:﹣2,
故写一个符合上述条件的点P的坐标可以为:(1,﹣2)(答案不唯一).
故答案为:(1,﹣2)(答案不唯一).
10.(4分)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,﹣2),“马”位于点(4,﹣2),则“炮”位于点 (1,0) .
【分析】直接利用已知点坐标建立平面直角坐标系,进而得出点的坐标.
【解答】解:如图所示:“炮”位于点(1,0).
故答案为:(1,0).
11.(4分)已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为 (﹣4,3) .
【分析】根据第二象限点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
【解答】解:∵点P在第二象限,且到x轴的距离为3,到y轴的距离为4,
∴点P的横坐标为﹣4,纵坐标为3,
∴点P的坐标为(﹣4,3).
故答案为:(﹣4,3).
12.(4分)如图所示是轰炸机机群的一个飞行队形,如果其中两架轰炸机的平面坐标分别表示为A(﹣2,3)和B(2,1),那么轰炸机C的平面坐标是 (﹣2,﹣1) .
【分析】根据A(﹣2,3)和B(2,1)的坐标以及与C的关系进行解答即可.
【解答】解:因为A(﹣2,3)和B(2,1),所以可建立如下图所示平面直角坐标系:
所以可得点C的坐标为(﹣2,﹣1),
故答案为:(﹣2,﹣1).
13.(4分)在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是 (﹣2,2) .
【分析】先求出点P到直线x=1的距离,再根据对称性求出对称点P′到直线x=1的距离,从而得到点P′的横坐标,即可得解.
【解答】解:∵点P(4,2),
∴点P到直线x=1的距离为4﹣1=3,∴点P关于直线x=1的对称点P′到直线x=1的距离为3,
∴点P′的横坐标为1﹣3=﹣2,
∴对称点P′的坐标为(﹣2,2).
故答案为:(﹣2,2).
14.(4分)如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y=于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=x于点B3;……按如此规律进行下去,点B2020的坐标为 (22020,22019) .
【分析】根据题意可以求得点B1的坐标,点A2的坐标,点B2的坐标,然后即可发现坐标变化的规律,从而可以求得点B2020的坐标.
【解答】解:由题意可得,点A1的坐标为(1,2),
设点B1的坐标为(a,a),
=,解得,a=2,
∴点B1的坐标为(2,1),
同理可得,点A2的坐标为(2,4),点B2的坐标为(4,2),
点A3的坐标为(4,8),点B3的坐标为(8,4),
……
∴点B2020的坐标为(22020,22019),
故答案为:(22020,22019).
三、解答题(15-18每题10分,19题12分,共52分)
15.(10分)在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(﹣3,1)、(﹣2,﹣3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立直角坐标系并确定点C的位置;
(2)若同学们打算从点B处直接赶往C处,请用方向角和距离描述点C相对于点B的位置.
【分析】(1)利用A,B点坐标得出原点位置,建立坐标系,进而得出C点位置;
(2)利用所画图形,进而结合勾股定理得出答案.
【解答】解:(1)根据A(﹣3,1),B(﹣2,﹣3)画出直角坐标系,
描出点C(3,2),如图所示;
(2)BC=5,所以点C在点B北偏东45°方向上,距离点B的5
km处.
16.(10分)已知点P(2m+4,m﹣1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过A(2,﹣4)点,且与x轴平行的直线上.
【分析】(1)让横坐标为0求得m的值,代入点P的坐标即可求解;
(2)让纵坐标﹣横坐标=3得m的值,代入点P的坐标即可求解;
(3)让纵坐标为﹣4求得m的值,代入点P的坐标即可求解.
【解答】解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3);
(2)令m﹣1﹣(2m+4)=3,解得m=﹣8,所以P点的坐标为(﹣12,﹣9);
(3)令m﹣1=﹣4,解得m=﹣3.所以P点的坐标为(﹣2,﹣4).
17.(10分)
如图,已知网格上最小的正方形的边长为1.
(1)求点A(﹣3,3)关于x轴的对称点的坐标是 (﹣3,﹣3) ;
(2)请作出△ABC关于直线x=1的对称图形△A′B′C′,并写出此时点B′的坐标 (7,1) (不写作法).
【分析】(1)根据关于x轴对称的点的坐标横坐标相同,纵坐标互为相反数解答即可;
(2)根据网格结构找出点A、B、C关于直线x=1的对称点A′、B′、C′的位置,然后顺次连接即可,再根据平面直角坐标系写出点B′的坐标.
【解答】解:(1)点A(﹣3,3)关于x轴的对称点的坐标是(﹣3,﹣3);
(2)如图所示,△A′B′C′即为所求作的三角形,
点B′(7,1).
故答案为:(﹣3,﹣3);(7,1).
18.(10分)在平面直角坐标系中,点P(x,y)经过某种变换后得到点P′(﹣y+1,x+2),我们把点P′(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1,P2,P3,P4,…,Pn.若点P1的坐标为(2,0).
(1)试写出P5的坐标;
(2)根据终结点的规律写出P2020的坐标.
【分析】利用点P(x,y)的终结点的定义分别写出点P2的坐标为(1,4),点P3的坐标为(﹣3,3),点P4的坐标为(﹣2,﹣1),点P5的坐标为(2,0),…,从而得到每4次变换一个循环,然后利用2020=4×505可判断点P2020的坐标与点P4的坐标相同.
【解答】解:(1)根据题意得点P1的坐标为(2,0),则点P2的坐标为(1,4),点P3的坐标为(﹣3,3),点P4的坐标为(﹣2,﹣1),点P5的坐标为(2,0),…,
(2)因为2020=4×505,
所以点P2020的坐标与点P4的坐标相同,为(﹣2,﹣1).
19.(12分)如图,网格中每个小正方形的边长都是1,依次完成下列各问:
(1)任选一点作为原点,建立平面直角坐标系;
(2)写出A、B、C、D、E各点的坐标;
(3)求五边形ABCDE的面积.
【分析】(1)根据坐标系的概念建立坐标系即可;
(2)由坐标系可得点的坐标;
(3)割补法求解即可.
【解答】解:(1)如图所示:
(2)A(0,2)、B(1,0)、C(3,0)、D(4,2)、E(3,3);
(3)S五边形ABCDE=3×4﹣×1×2﹣×1×2﹣×1×3﹣×1×1
=12﹣1﹣1﹣1.5﹣0.5
=8
位置与坐标
一、选择题(每小题3分,共24分)
1.已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )
A.(4,0)
B.(0,4)
C.(﹣4,0)
D.(0,﹣4)
2.在平面直角坐标系中,将点A(3,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(1,1)
B.(3,1)
C.(1,2)
D.(1,﹣5)
3.在平面直角坐标系中,已知点A(﹣4,3)与点B关于原点对称,则点B的坐标为( )
A.(﹣4,﹣3)
B.(4,3)
C.(4,﹣3)
D.(﹣4,3)
4.在平面直角坐标系中,点P(m,2m﹣2),则点P不可能在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
5.如图,若在象棋盘上建立平面直角坐标系xOy,使“帅”的坐标为(﹣1,﹣2)“马”的坐标为(2,﹣2),则“兵”的坐标为( )
A.(﹣3,1)
B.(﹣2,1)
C.(﹣3,0)
D.(﹣2,3)
6.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°)
B.Q(3,﹣120°)
C.Q(3,600°)
D.Q(3,﹣500°)
7.已知点P(a﹣3,2﹣a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
8.在平面直角坐标系中,若点P(m﹣2,m+1)在第二象限,则m的取值范围是( )
A.m<﹣1
B.m>2
C.﹣1<m<2
D.m>﹣1
二、填空题(每小题4分,共24分)
9.(4分)已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标
.
10.(4分)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,﹣2),“马”位于点(4,﹣2),则“炮”位于点
.
11.(4分)已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为
.
12.(4分)如图所示是轰炸机机群的一个飞行队形,如果其中两架轰炸机的平面坐标分别表示为A(﹣2,3)和B(2,1),那么轰炸机C的平面坐标是
.
13.(4分)在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是
.
14.(4分)如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y=于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=x于点B3;……按如此规律进行下去,点B2020的坐标为
.
三、解答题(15-18每题10分,19题12分,共52分)
15.(10分)在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(﹣3,1)、(﹣2,﹣3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立直角坐标系并确定点C的位置;
(2)若同学们打算从点B处直接赶往C处,请用方向角和距离描述点C相对于点B的位置.
16.(10分)已知点P(2m+4,m﹣1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过A(2,﹣4)点,且与x轴平行的直线上.
17.(10分)
如图,已知网格上最小的正方形的边长为1.
(1)求点A(﹣3,3)关于x轴的对称点的坐标是
;
(2)请作出△ABC关于直线x=1的对称图形△A′B′C′,并写出此时点B′的坐标
(不写作法).
18.(10分)在平面直角坐标系中,点P(x,y)经过某种变换后得到点P′(﹣y+1,x+2),我们把点P′(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1,P2,P3,P4,…,Pn.若点P1的坐标为(2,0).
(1)试写出P5的坐标;
(2)根据终结点的规律写出P2020的坐标.
19.(12分)如图,网格中每个小正方形的边长都是1,依次完成下列各问:
(1)任选一点作为原点,建立平面直角坐标系;
(2)写出A、B、C、D、E各点的坐标;
(3)求五边形ABCDE的面积.
参考答案与试题解析
一、选择题(每小题3分,共24分)
1.已知点P(m+2,2m﹣4)在x轴上,则点P的坐标是( )
A.(4,0)
B.(0,4)
C.(﹣4,0)
D.(0,﹣4)
【分析】直接利用关于x轴上点的坐标特点得出m的值,进而得出答案.
【解答】解:∵点P(m+2,2m﹣4)在x轴上,
∴2m﹣4=0,
解得:m=2,
∴m+2=4,
则点P的坐标是:(4,0).
故选:A.
2.在平面直角坐标系中,将点A(3,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A′,则点A′的坐标是( )
A.(1,1)
B.(3,1)
C.(1,2)
D.(1,﹣5)
【分析】根据向左平移横坐标减,向上平移纵坐标加求解即可.
【解答】解:将点A(3,﹣2)向上平移3个单位长度,再向左平移2个单位长度,得到点A'的坐标为(3﹣2,﹣2+3),即(1,1),
故选:A.
3.在平面直角坐标系中,已知点A(﹣4,3)与点B关于原点对称,则点B的坐标为( )
A.(﹣4,﹣3)
B.(4,3)
C.(4,﹣3)
D.(﹣4,3)
【分析】根据关于原点的对称点,横、纵坐标都变成相反数解答.
【解答】解:∵点A(﹣4,3),点A与点B关于原点对称,
∴点B(4,﹣3).
故选:C.
4.在平面直角坐标系中,点P(m,2m﹣2),则点P不可能在( )
A.第一象限
B.第二象限
C.第三象限
D.第四象限
【分析】依据不同象限内点的坐标的符号特征分四种情况讨论,即可得到点P可能的位置.
【解答】解:当m>1时,2m﹣2>0,故点P可能在第一象限;
当m<0时,2m﹣2<0,故点P不可能在第二象限;
当m<0时,2m﹣2<0,故点P可能在第三象限;
当0<m<1时,2m﹣2<0,故点P可能在第四象限;
故选:B.
5.如图,若在象棋盘上建立平面直角坐标系xOy,使“帅”的坐标为(﹣1,﹣2)“马”的坐标为(2,﹣2),则“兵”的坐标为( )
A.(﹣3,1)
B.(﹣2,1)
C.(﹣3,0)
D.(﹣2,3)
【分析】直接利用“帅”位于点(﹣1,﹣2),可得原点的位置,进而得出“兵”的坐标.
【解答】解:如图所示:可得“炮”是原点,
则“兵”位于点:(﹣3,1).
故选:A.
6.在平面内由极点、极轴和极径组成的坐标系叫做极坐标系.如图,在平面上取定一点O称为极点;从点O出发引一条射线Ox称为极轴;线段OP的长度称为极径.点P的极坐标就可以用线段OP的长度以及从Ox转动到OP的角度(规定逆时针方向转动角度为正)来确定,即P(3,60°)或P(3,﹣300°)或P(3,420°)等,则点P关于点O成中心对称的点Q的极坐标表示不正确的是( )
A.Q(3,240°)
B.Q(3,﹣120°)
C.Q(3,600°)
D.Q(3,﹣500°)
【分析】根据中心对称的性质解答即可.
【解答】解:∵P(3,60°)或P(3,﹣300°)或P(3,420°),
由点P关于点O成中心对称的点Q可得:点Q的极坐标为(3,240°),(3,﹣120°),(3,600°),
故选:D.
7.已知点P(a﹣3,2﹣a)关于原点对称的点在第四象限,则a的取值范围在数轴上表示正确的是( )
A.
B.
C.
D.
【分析】直接利用关于原点对称点的性质得出关于a的不等式组进而求出答案.
【解答】解:∵点P(a﹣3,2﹣a)关于原点对称的点在第四象限,
∴点P(a﹣3,2﹣a)在第二象限,
∴,
解得:a<2.
则a的取值范围在数轴上表示正确的是:.
故选:C.
8.在平面直角坐标系中,若点P(m﹣2,m+1)在第二象限,则m的取值范围是( )
A.m<﹣1
B.m>2
C.﹣1<m<2
D.m>﹣1
【分析】根据第二象限内点的横坐标是负数,纵坐标是正数列出不等式组求解即可.
【解答】解:∵点P(m﹣2,m+1)在第二象限,
∴,
解得﹣1<m<2.
故选:C.
二、填空题(每小题4分,共24分)
9.(4分)已知点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),写出一个符合上述条件的点P的坐标 (1,﹣2)(答案不唯一) .
【分析】直接利用第四象限内点的坐标特点得出x,y的取值范围,进而得出答案.
【解答】解:∵点P(x,y)位于第四象限,并且x≤y+4(x,y为整数),
∴x>0,y<0,
∴当x=1时,1≤y+4,
解得:0>y≥﹣3,
∴y可以为:﹣2,
故写一个符合上述条件的点P的坐标可以为:(1,﹣2)(答案不唯一).
故答案为:(1,﹣2)(答案不唯一).
10.(4分)中国象棋是中华民族的文化瑰宝,因趣味性强,深受大众喜爱.如图,若在象棋棋盘上建立平面直角坐标系,使“帅”位于点(0,﹣2),“马”位于点(4,﹣2),则“炮”位于点 (1,0) .
【分析】直接利用已知点坐标建立平面直角坐标系,进而得出点的坐标.
【解答】解:如图所示:“炮”位于点(1,0).
故答案为:(1,0).
11.(4分)已知在平面直角坐标系中,点P在第二象限,且到x轴的距离为3,到y轴的距离为4,则点P的坐标为 (﹣4,3) .
【分析】根据第二象限点的横坐标是负数,纵坐标是正数,点到x轴的距离等于纵坐标的长度,到y轴的距离等于横坐标的长度解答.
【解答】解:∵点P在第二象限,且到x轴的距离为3,到y轴的距离为4,
∴点P的横坐标为﹣4,纵坐标为3,
∴点P的坐标为(﹣4,3).
故答案为:(﹣4,3).
12.(4分)如图所示是轰炸机机群的一个飞行队形,如果其中两架轰炸机的平面坐标分别表示为A(﹣2,3)和B(2,1),那么轰炸机C的平面坐标是 (﹣2,﹣1) .
【分析】根据A(﹣2,3)和B(2,1)的坐标以及与C的关系进行解答即可.
【解答】解:因为A(﹣2,3)和B(2,1),所以可建立如下图所示平面直角坐标系:
所以可得点C的坐标为(﹣2,﹣1),
故答案为:(﹣2,﹣1).
13.(4分)在平面直角坐标系中,点P(4,2)关于直线x=1的对称点的坐标是 (﹣2,2) .
【分析】先求出点P到直线x=1的距离,再根据对称性求出对称点P′到直线x=1的距离,从而得到点P′的横坐标,即可得解.
【解答】解:∵点P(4,2),
∴点P到直线x=1的距离为4﹣1=3,∴点P关于直线x=1的对称点P′到直线x=1的距离为3,
∴点P′的横坐标为1﹣3=﹣2,
∴对称点P′的坐标为(﹣2,2).
故答案为:(﹣2,2).
14.(4分)如图,平面直角坐标系中,点A1的坐标为(1,2),以O为圆心,OA1长为半径画弧,交直线y=于点B1.过点B1作B1A2∥y轴交直线y=2x于点A2,以O为圆心,OA2长为半径画弧,交直线y═x于点B2;过点B2作B2A3∥y轴交直线y=2x于点A3,以点O为圆心,OA3长为半径画弧,交直线y=x于点B3;……按如此规律进行下去,点B2020的坐标为 (22020,22019) .
【分析】根据题意可以求得点B1的坐标,点A2的坐标,点B2的坐标,然后即可发现坐标变化的规律,从而可以求得点B2020的坐标.
【解答】解:由题意可得,点A1的坐标为(1,2),
设点B1的坐标为(a,a),
=,解得,a=2,
∴点B1的坐标为(2,1),
同理可得,点A2的坐标为(2,4),点B2的坐标为(4,2),
点A3的坐标为(4,8),点B3的坐标为(8,4),
……
∴点B2020的坐标为(22020,22019),
故答案为:(22020,22019).
三、解答题(15-18每题10分,19题12分,共52分)
15.(10分)在一次夏令营活动中,老师将一份行动计划藏在没有任何标记的点C处,只告诉大家两个标志点A,B的坐标分别为(﹣3,1)、(﹣2,﹣3),以及点C的坐标为(3,2)(单位:km).
(1)请在图中建立直角坐标系并确定点C的位置;
(2)若同学们打算从点B处直接赶往C处,请用方向角和距离描述点C相对于点B的位置.
【分析】(1)利用A,B点坐标得出原点位置,建立坐标系,进而得出C点位置;
(2)利用所画图形,进而结合勾股定理得出答案.
【解答】解:(1)根据A(﹣3,1),B(﹣2,﹣3)画出直角坐标系,
描出点C(3,2),如图所示;
(2)BC=5,所以点C在点B北偏东45°方向上,距离点B的5
km处.
16.(10分)已知点P(2m+4,m﹣1),试分别根据下列条件,求出点P的坐标.
(1)点P在y轴上;
(2)点P的纵坐标比横坐标大3;
(3)点P在过A(2,﹣4)点,且与x轴平行的直线上.
【分析】(1)让横坐标为0求得m的值,代入点P的坐标即可求解;
(2)让纵坐标﹣横坐标=3得m的值,代入点P的坐标即可求解;
(3)让纵坐标为﹣4求得m的值,代入点P的坐标即可求解.
【解答】解:(1)令2m+4=0,解得m=﹣2,所以P点的坐标为(0,﹣3);
(2)令m﹣1﹣(2m+4)=3,解得m=﹣8,所以P点的坐标为(﹣12,﹣9);
(3)令m﹣1=﹣4,解得m=﹣3.所以P点的坐标为(﹣2,﹣4).
17.(10分)
如图,已知网格上最小的正方形的边长为1.
(1)求点A(﹣3,3)关于x轴的对称点的坐标是 (﹣3,﹣3) ;
(2)请作出△ABC关于直线x=1的对称图形△A′B′C′,并写出此时点B′的坐标 (7,1) (不写作法).
【分析】(1)根据关于x轴对称的点的坐标横坐标相同,纵坐标互为相反数解答即可;
(2)根据网格结构找出点A、B、C关于直线x=1的对称点A′、B′、C′的位置,然后顺次连接即可,再根据平面直角坐标系写出点B′的坐标.
【解答】解:(1)点A(﹣3,3)关于x轴的对称点的坐标是(﹣3,﹣3);
(2)如图所示,△A′B′C′即为所求作的三角形,
点B′(7,1).
故答案为:(﹣3,﹣3);(7,1).
18.(10分)在平面直角坐标系中,点P(x,y)经过某种变换后得到点P′(﹣y+1,x+2),我们把点P′(﹣y+1,x+2)叫做点P(x,y)的终结点.已知点P1的终结点为P2,点P2的终结点为P3,点P3的终结点为P4,这样依次得到P1,P2,P3,P4,…,Pn.若点P1的坐标为(2,0).
(1)试写出P5的坐标;
(2)根据终结点的规律写出P2020的坐标.
【分析】利用点P(x,y)的终结点的定义分别写出点P2的坐标为(1,4),点P3的坐标为(﹣3,3),点P4的坐标为(﹣2,﹣1),点P5的坐标为(2,0),…,从而得到每4次变换一个循环,然后利用2020=4×505可判断点P2020的坐标与点P4的坐标相同.
【解答】解:(1)根据题意得点P1的坐标为(2,0),则点P2的坐标为(1,4),点P3的坐标为(﹣3,3),点P4的坐标为(﹣2,﹣1),点P5的坐标为(2,0),…,
(2)因为2020=4×505,
所以点P2020的坐标与点P4的坐标相同,为(﹣2,﹣1).
19.(12分)如图,网格中每个小正方形的边长都是1,依次完成下列各问:
(1)任选一点作为原点,建立平面直角坐标系;
(2)写出A、B、C、D、E各点的坐标;
(3)求五边形ABCDE的面积.
【分析】(1)根据坐标系的概念建立坐标系即可;
(2)由坐标系可得点的坐标;
(3)割补法求解即可.
【解答】解:(1)如图所示:
(2)A(0,2)、B(1,0)、C(3,0)、D(4,2)、E(3,3);
(3)S五边形ABCDE=3×4﹣×1×2﹣×1×2﹣×1×3﹣×1×1
=12﹣1﹣1﹣1.5﹣0.5
=8
