苏科版七年级上册数学4.1从问题到方程课件 (共21张)
文档属性
| 名称 | 苏科版七年级上册数学4.1从问题到方程课件 (共21张) |

|
|
| 格式 | zip | ||
| 文件大小 | 476.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
§4.1
从问题到方程
学习目标:
1.探索实际问题中的数量关系,并用方程描述,初步感受方程是刻画现实世界的有效模型;
2.通过观察,归纳方程、一元一次方程的概念。
问题情境
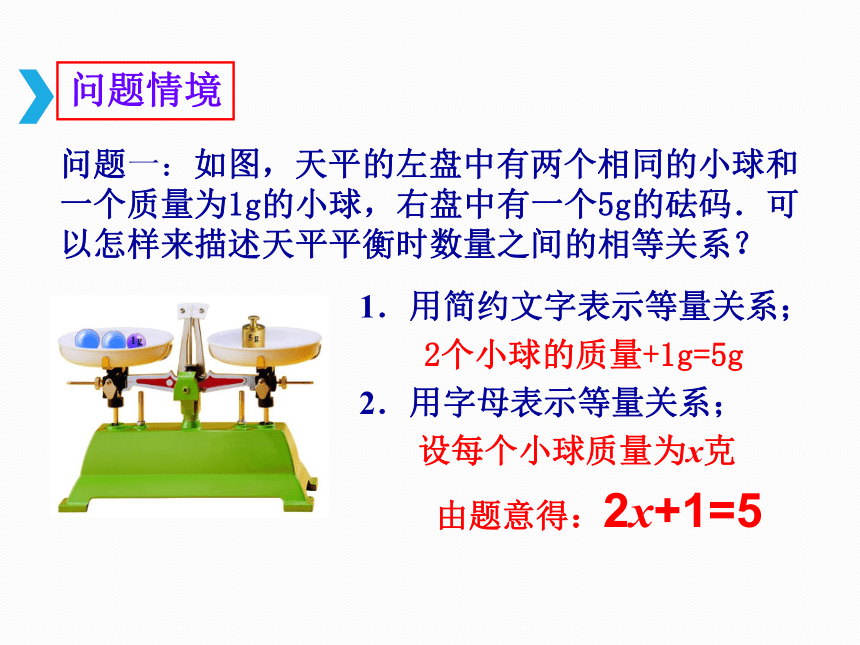
问题一:如图,天平的左盘中有两个相同的小球和一个质量为1g的小球,右盘中有一个5g的砝码.可以怎样来描述天平平衡时数量之间的相等关系?
1.用简约文字表示等量关系;
2个小球的质量+1g=5g
2.用字母表示等量关系;
设每个小球质量为x克
由题意得:2x+1=5
问题二:篮球联赛规则规定:胜一场得2分,负一场得1分.某篮球队赛了12场,共得20分.怎样描述其中数量之间的相等关系?
问题情境
1.用简约文字表示等量关系;
胜场得分+负场得分=20分
2.用字母表示等量关系;
设该篮球队胜了x场,
则该篮球队负了
场
由题意得:
2x+(12-x)=20
2x+1=5
2x+(12-x)=20
以上两个含x的等式你在小学见过吗?
他们有什么特征?
含有未知数
等式
的
叫做方程。
方程的概念:
归纳
通过比较可以看出,用
描述问题中的相等关系最简明。
比较上述两个问题,表示问题中的相等关系,哪一种最简明?
问题
方程
相等关系
方程
探究学习(一)
活动一
我国古代问题:以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
这段话的意思是:
用绳子量井深,把绳三折来量,井外余绳有四尺;把绳四折来量,井外余绳有一尺.绳长、井深各几尺?
以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
思考一:
若设绳长为x尺,则井深有哪几种不同的表示方法?
依据是
以绳三折测之,绳多四尺
依据是
将绳四折测之,绳多一尺
由此可列方程:
思考二:
若设井深为y尺,则绳长有哪几种不同的表示方法?
由此可列出什么方程?
以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
以绳三折测之,绳多四尺;若将绳四折测之,
绳多一尺.绳长、井深各几何?
设井深为y尺
设绳长为x尺
观察与思考
探究学习(二)
活动二
用火柴棒按如下方式搭小鱼
8+6(n-1)
(1)用代数式表示搭n条小鱼需要火柴棒根数
(2)若搭n条小鱼用了140根火柴棒,怎样用方程描述其中数量之间的相等关系?
8+6(n-1)=140
观察前面所得的方程,它们有什么共同特点?
探究新知
1、只含有一个未知数;
2、未知数的次数都是1次。
2x+1=5
2x+(12-x)=20
8+6(n-1)=140
概念学习
只含有一个未知数,并且未知数的次数都是1的方程,叫一元一次方程.
如果方程
是关于x的一元一次方程,那么m=
。
变式1.如果方程
是关于x的一元一次方程,那么m=
。
变式2.如果方程
是关于x的一元一次方程,那么m=
。
2
-1
-1
未知数前系数不为0
例题
通过本节课,
我学到了……
全课小结
1.方程的概念
含有未知数的等式叫做方程。
全课小结
2.从问题到方程
①审题
找数量关系
②设未知数
③列方程
3.一元一次方程的概念
只含有一个未知数,并且未知数的次数都
是1的方程,叫做一元一次方程。
√
×
√
×
×
×
×
判断依据
1.判断下列各式是否为一元一次方程,若不是,请说明理由。
练一练
1.判断下列各式是否为一元一次方程,若不是,请说明理由。
√
×
√
×
×
×
×
判断依据
①方程中只含一个未知数;
②未知数的次数为1;
②方程两边为整式;
④一元一次方程为等式
练一练
2.
今年小红5岁,爸爸32岁。
(1)x年后,小红
岁,爸爸
岁;
(2)如果x年后小红的年龄是爸爸年龄的
,怎样列方程?
3.把50㎏大米分装在3个同样大小的袋子里,装满后还剩余5㎏。设每个袋子可以装大米x㎏,可得方程
。
练一练
练一练
4.甲乙两城市间的铁路经过技术改造,列车运行速度从100
km/h提高到120km/h,运行时间缩短了2
h.
①设原运行时间为xh,可得方程
;
②设甲乙两城市间的路程为ykm
,可得方程
。
5.甲、乙两人分别用面值为20元和10元的人民币购买一本同样的书,甲找回的钱是乙找回钱的6倍,设这本书的价格为x元,可得方程
。
谢
谢
!
§4.1
从问题到方程
学习目标:
1.探索实际问题中的数量关系,并用方程描述,初步感受方程是刻画现实世界的有效模型;
2.通过观察,归纳方程、一元一次方程的概念。
问题情境
问题一:如图,天平的左盘中有两个相同的小球和一个质量为1g的小球,右盘中有一个5g的砝码.可以怎样来描述天平平衡时数量之间的相等关系?
1.用简约文字表示等量关系;
2个小球的质量+1g=5g
2.用字母表示等量关系;
设每个小球质量为x克
由题意得:2x+1=5
问题二:篮球联赛规则规定:胜一场得2分,负一场得1分.某篮球队赛了12场,共得20分.怎样描述其中数量之间的相等关系?
问题情境
1.用简约文字表示等量关系;
胜场得分+负场得分=20分
2.用字母表示等量关系;
设该篮球队胜了x场,
则该篮球队负了
场
由题意得:
2x+(12-x)=20
2x+1=5
2x+(12-x)=20
以上两个含x的等式你在小学见过吗?
他们有什么特征?
含有未知数
等式
的
叫做方程。
方程的概念:
归纳
通过比较可以看出,用
描述问题中的相等关系最简明。
比较上述两个问题,表示问题中的相等关系,哪一种最简明?
问题
方程
相等关系
方程
探究学习(一)
活动一
我国古代问题:以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
这段话的意思是:
用绳子量井深,把绳三折来量,井外余绳有四尺;把绳四折来量,井外余绳有一尺.绳长、井深各几尺?
以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
思考一:
若设绳长为x尺,则井深有哪几种不同的表示方法?
依据是
以绳三折测之,绳多四尺
依据是
将绳四折测之,绳多一尺
由此可列方程:
思考二:
若设井深为y尺,则绳长有哪几种不同的表示方法?
由此可列出什么方程?
以绳三折测之,绳多四尺;若将绳四折测之,绳多一尺.绳长、井深各几何?
以绳三折测之,绳多四尺;若将绳四折测之,
绳多一尺.绳长、井深各几何?
设井深为y尺
设绳长为x尺
观察与思考
探究学习(二)
活动二
用火柴棒按如下方式搭小鱼
8+6(n-1)
(1)用代数式表示搭n条小鱼需要火柴棒根数
(2)若搭n条小鱼用了140根火柴棒,怎样用方程描述其中数量之间的相等关系?
8+6(n-1)=140
观察前面所得的方程,它们有什么共同特点?
探究新知
1、只含有一个未知数;
2、未知数的次数都是1次。
2x+1=5
2x+(12-x)=20
8+6(n-1)=140
概念学习
只含有一个未知数,并且未知数的次数都是1的方程,叫一元一次方程.
如果方程
是关于x的一元一次方程,那么m=
。
变式1.如果方程
是关于x的一元一次方程,那么m=
。
变式2.如果方程
是关于x的一元一次方程,那么m=
。
2
-1
-1
未知数前系数不为0
例题
通过本节课,
我学到了……
全课小结
1.方程的概念
含有未知数的等式叫做方程。
全课小结
2.从问题到方程
①审题
找数量关系
②设未知数
③列方程
3.一元一次方程的概念
只含有一个未知数,并且未知数的次数都
是1的方程,叫做一元一次方程。
√
×
√
×
×
×
×
判断依据
1.判断下列各式是否为一元一次方程,若不是,请说明理由。
练一练
1.判断下列各式是否为一元一次方程,若不是,请说明理由。
√
×
√
×
×
×
×
判断依据
①方程中只含一个未知数;
②未知数的次数为1;
②方程两边为整式;
④一元一次方程为等式
练一练
2.
今年小红5岁,爸爸32岁。
(1)x年后,小红
岁,爸爸
岁;
(2)如果x年后小红的年龄是爸爸年龄的
,怎样列方程?
3.把50㎏大米分装在3个同样大小的袋子里,装满后还剩余5㎏。设每个袋子可以装大米x㎏,可得方程
。
练一练
练一练
4.甲乙两城市间的铁路经过技术改造,列车运行速度从100
km/h提高到120km/h,运行时间缩短了2
h.
①设原运行时间为xh,可得方程
;
②设甲乙两城市间的路程为ykm
,可得方程
。
5.甲、乙两人分别用面值为20元和10元的人民币购买一本同样的书,甲找回的钱是乙找回钱的6倍,设这本书的价格为x元,可得方程
。
谢
谢
!
同课章节目录
- 第1章 我们与数学同行
- 1.1 生活 数学
- 1.2 活动 思考
- 第2章 有理数
- 2.1 正数与负数
- 2.2 有理数与无理数
- 2.3 数轴
- 2.4 绝对值与相反数
- 2.5 有理数的加法与减法
- 2.6 有理数的乘法与除法
- 2.7 有理数的乘方
- 2.8 有理数的混合运算
- 第3章 代数式
- 3.1 字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 3.4 合并同类项
- 3.5 去括号
- 3.6 整式的加减
- 第4章 一元一次方程
- 4.1 从问题到方程
- 4.2 解一元一次方程
- 4.3 用一元一次方程解决问题
- 第5章 走进图形世界
- 5.1 丰富的图形世界
- 5.2 图形的运动
- 5.3 展开与折叠
- 5.4 主视图、左视图、俯视图
- 第6章 平面图形的认识(一)
- 6.1 线段 射线 直线
- 6.2 角
- 6.3 余角 补角 对顶角
- 6.4 平行
- 6.5 垂直
