人教版八年级上册数学课件:13.3.1等腰三角形(第一课时 25张)
文档属性
| 名称 | 人教版八年级上册数学课件:13.3.1等腰三角形(第一课时 25张) |

|
|
| 格式 | zip | ||
| 文件大小 | 834.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
学习目标:
1.探索并掌握等腰三角形的两个性质.
2.会运用等腰三角形的概念和性质解决有关问题。
重点:等腰三角形性质及其简单应用.
难点:等腰三角形的“三线合一”的性质的理解及其应用。
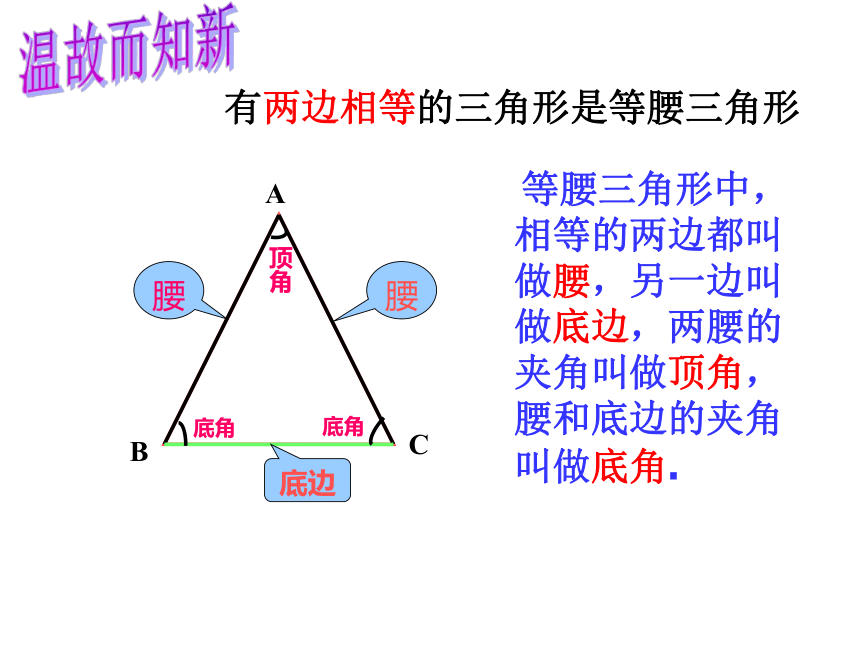
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
有两边相等的三角形是等腰三角形
1、等腰三角形一腰为3cm,底为4cm,则它的周长是
;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是
;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是
。
比一比,看谁做的快又准!
10cm
10cm或11cm
19cm
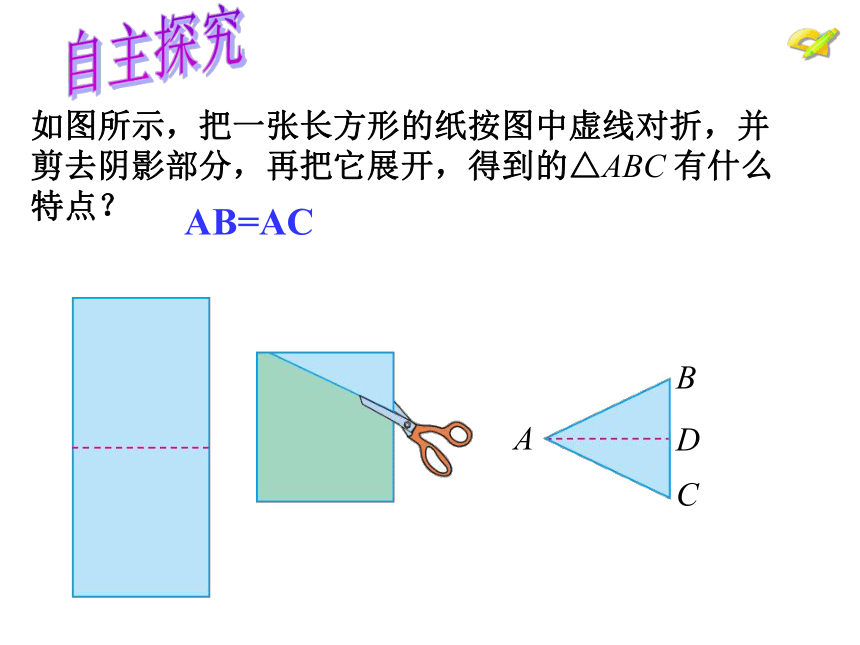
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC
有什么特点?
A
B
C
D
AB=AC
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B
=
∠C.
∠BAD
=
∠CAD
∠ADB
=
∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗?
大胆猜想
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
等腰三角形的两个底角相等
猜想与论证
A
B
C
则∠ADB=∠ADC
=90?
D
在Rt△ABD和Rt△ACD中
证明:
作BC边上
的高AD
AB=AC
AD=AD
(公共边)
∴
Rt△ABD≌Rt△ACD
(HL)
∴
∠B=∠C
(全等三角形对应角相等)
A
B
C
则有
BD=CD
D
在△ABD和△ACD中
证明:
作△ABC
的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SSS)
∴
∠B=∠C
(全等三角形对应角相等)
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明:
作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SAS)
∴
∠B=∠C
(全等三角形对应角相等)
D
如图,作△ABC的中线AD
D
┌
如图,
作△ABC
的高AD
D
如图,作顶角
的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
想一想:
由刚才证明的△ABD≌
△ACD,除了能得到∠B=∠C
你还能发现什么?
重合的线段
重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B
=
∠C.
∠BAD
=
∠CAD
∠ADB
=∠ADC
=90°
等腰三角形的性质
性质
1
等腰三角形的两个底角相等
(简写成等边对等角)
性质
2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
(简写成三线合一)
性质
1
在△ABC中,
∵
AB=AC
∴
________=
________
性质
2
(
1
)
∵
AB=AC,AD是角平分线,
∴______⊥______,________=________
;
(
2
)
∵
AB=AC
,AD是中线,
∴
⊥
,∠
=
∠____;
(
3
)
∵
AB=AC
,AD⊥BC,
∴∠_____=∠______,_____=______
几何语言:
∠B
∠C
AD
BC
BD
CD
AD
BC
BAD
CAD
BAD
CAD
BD
CD
⒈等腰三角形一个底角为75°,它的另外两个
角为_____
__;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个
角为______
__。
75°,
30°
70°,40°或55°,55°
35°,35°
尝试运用
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
例题:如图,在△ABC中
,AB=AC,点D在AC
上,且BD=BC=AD.
求△ABC各内角的度数?
当堂检测
(1)如图,△ABC
中,
AB
=AC,
∠A
=36°,
则∠B
=
;
(2)如图,△ABC
中,
AB
=AC,
∠A
=3
∠B,
则∠A
=
;
(3)等腰三角形一个角为40°,它的另外两个角为___________________
A
B
C
A
B
C
70°,70°或40°,100°
108°
72°
第一题图
第二题图
如图,AB=AC,∠A=40°,AB的垂直平分线交AC于D,则∠DBC的度数为
。
当堂检测
30°
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合一”
2.
能根据等腰三角形的概念与性质求等腰三角形的周长或知道一角求其它两角或证线段、角相等。
习题13.3
第1、4题
等腰三角形底边中点到两腰
的距离相等吗?
A
B
C
D
E
F
课后思考:
学习目标:
1.探索并掌握等腰三角形的两个性质.
2.会运用等腰三角形的概念和性质解决有关问题。
重点:等腰三角形性质及其简单应用.
难点:等腰三角形的“三线合一”的性质的理解及其应用。
等腰三角形中,相等的两边都叫做腰,另一边叫做底边,两腰的夹角叫做顶角,腰和底边的夹角叫做底角.
A
C
B
腰
腰
底边
顶角
底角
底角
有两边相等的三角形是等腰三角形
1、等腰三角形一腰为3cm,底为4cm,则它的周长是
;
2、等腰三角形的一边长为3cm,另一边长为4cm,则它的周长是
;
3、等腰三角形的一边长为3cm,另一边长为8cm,则它的周长是
。
比一比,看谁做的快又准!
10cm
10cm或11cm
19cm
如图所示,把一张长方形的纸按图中虚线对折,并剪去阴影部分,再把它展开,得到的△ABC
有什么特点?
A
B
C
D
AB=AC
把剪出的等腰三角形ABC沿折痕对折,找出其中重合的线段和角.
等腰三角形是轴对称图形吗?
重合的线段
重合的角
A
C
B
D
AB=AC
BD=CD
AD=AD
∠B
=
∠C.
∠BAD
=
∠CAD
∠ADB
=
∠ADC
等腰三角形除了两腰相等以外,
你还能发现它的其他性质吗?
大胆猜想
已知:△ABC中,AB=AC
求证:∠B=?C
分析:1.如何证明两个角相等?
2.如何构造两个全等的三角形?
A
B
C
D
等腰三角形的两个底角相等
猜想与论证
A
B
C
则∠ADB=∠ADC
=90?
D
在Rt△ABD和Rt△ACD中
证明:
作BC边上
的高AD
AB=AC
AD=AD
(公共边)
∴
Rt△ABD≌Rt△ACD
(HL)
∴
∠B=∠C
(全等三角形对应角相等)
A
B
C
则有
BD=CD
D
在△ABD和△ACD中
证明:
作△ABC
的中线AD
AB=AC
BD=CD
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SSS)
∴
∠B=∠C
(全等三角形对应角相等)
A
B
C
则有∠1=∠2
D
1
2
在△ABD和△ACD中
证明:
作顶角的平分线AD,
AB=AC
∠1=∠2
AD=AD
(公共边)
∴
△ABD≌
△ACD
(SAS)
∴
∠B=∠C
(全等三角形对应角相等)
D
如图,作△ABC的中线AD
D
┌
如图,
作△ABC
的高AD
D
如图,作顶角
的平分线AD.
A
B
C
A
B
C
A
B
C
等腰三角形常见辅助线
想一想:
由刚才证明的△ABD≌
△ACD,除了能得到∠B=∠C
你还能发现什么?
重合的线段
重合的角
A
B
D
C
AB=AC
BD=CD
AD=AD
∠B
=
∠C.
∠BAD
=
∠CAD
∠ADB
=∠ADC
=90°
等腰三角形的性质
性质
1
等腰三角形的两个底角相等
(简写成等边对等角)
性质
2
等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合
(简写成三线合一)
性质
1
在△ABC中,
∵
AB=AC
∴
________=
________
性质
2
(
1
)
∵
AB=AC,AD是角平分线,
∴______⊥______,________=________
;
(
2
)
∵
AB=AC
,AD是中线,
∴
⊥
,∠
=
∠____;
(
3
)
∵
AB=AC
,AD⊥BC,
∴∠_____=∠______,_____=______
几何语言:
∠B
∠C
AD
BC
BD
CD
AD
BC
BAD
CAD
BAD
CAD
BD
CD
⒈等腰三角形一个底角为75°,它的另外两个
角为_____
__;
⒉等腰三角形一个角为70°,它的另外两个角
为___________________;
⒊等腰三角形一个角为110°,它的另外两个
角为______
__。
75°,
30°
70°,40°或55°,55°
35°,35°
尝试运用
A
B
C
D
x
⌒
2x
⌒
2x
⌒
⌒
2x
例题:如图,在△ABC中
,AB=AC,点D在AC
上,且BD=BC=AD.
求△ABC各内角的度数?
当堂检测
(1)如图,△ABC
中,
AB
=AC,
∠A
=36°,
则∠B
=
;
(2)如图,△ABC
中,
AB
=AC,
∠A
=3
∠B,
则∠A
=
;
(3)等腰三角形一个角为40°,它的另外两个角为___________________
A
B
C
A
B
C
70°,70°或40°,100°
108°
72°
第一题图
第二题图
如图,AB=AC,∠A=40°,AB的垂直平分线交AC于D,则∠DBC的度数为
。
当堂检测
30°
轴对称图形
两个底角相等,简称“等边对等角”
顶角平分线、底边上的中线、和底边上的高互相重合,简称“三线合一”
2.
能根据等腰三角形的概念与性质求等腰三角形的周长或知道一角求其它两角或证线段、角相等。
习题13.3
第1、4题
等腰三角形底边中点到两腰
的距离相等吗?
A
B
C
D
E
F
课后思考:
