高二物理人教版选修3-1学案 第2章 实验:测定金属的电阻率 Word版含解析
文档属性
| 名称 | 高二物理人教版选修3-1学案 第2章 实验:测定金属的电阻率 Word版含解析 |

|
|
| 格式 | doc | ||
| 文件大小 | 584.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览



文档简介
实验:测定金属的电阻率
实验步骤
1.直径测定
用螺旋测微器在被测金属导线上的三个不同位置各测一次直径,求出其平均值d,计算出导线的横截面积S=。
2.电路连接
按如图所示的原理电路图连接好用伏安法测电阻的实验电路。
3.长度测量
用毫米刻度尺测量接入电路中的被测金属导线的有效长度,反复测量3次,求出其平均值l。
4.U、I测量
把滑动变阻器的滑动片调节到使接入电路中的电阻值最大的位置,电路经检查确认无误后,闭合开关S,改变滑动变阻器滑动片的位置,读出几组相应的电流表、电压表的示数I和U的值,记入表格内,断开开关S。
5.拆去实验线路,整理好实验器材。
五、数据处理
1.在求Rx的平均值时可用两种方法
(1)用Rx=分别算出各次的数值,再取平均值。
(2)用U?I图线的斜率求出。
2.计算电阻率
将记录的数据Rx、l、d的值代入电阻率计算式ρ=Rx=。
六、误差分析
1.金属丝的横截面积是利用直径计算而得,直径的测量是产生误差的主要来源之一。
2.采用伏安法测量金属丝的电阻时,由于采用的是电流表外接法,测量值小于真实值,使电阻率的测量值偏小。
3.金属丝的长度测量、电流表和电压表的读数等会带来偶然误差。
4.由于金属丝通电后发热升温,会使金属丝的电阻率变大,造成测量误差。
七、注意事项
1.本实验中被测金属导线的电阻值较小,因此实验电路一般采用电流表外接法。
2.实验连线时,应先从电源的正极出发,依次将电源、开关、电流表、待测金属导线、滑动变阻器连成主干线路,然后再把电压表并联在待测金属导线的两端。
3.测量被测金属导线的有效长度,是指测量待测导线接入电路的两个端点之间的长度,亦即电压表两端点间的待测导线长度,测量时应将导线拉直,反复测量三次,求其平均值。
4.测金属导线直径一定要选三个不同部位进行测量,求其平均值。
5.闭合开关S之前,一定要使滑动变阻器的滑片处在有效电阻值最大的位置。
6.在用伏安法测电阻时,通过待测导线的电流强度I不宜过大(电流表用0~0.6 A量程),通电时间不宜过长,以免金属导线的温度明显升高,造成其电阻率在实验过程中逐渐增大。
7.求Rx的平均值时可用两种方法:第一种是用Rx=算出各次的测量值,再取平均值;第二种是用图象(U?I图线)来求出。若采用图象法,在描点时,要尽量使各点间的距离拉大一些,连线时要尽可能地让各点均匀分布在直线的两侧,个别明显偏离较远的点可以不予考虑。
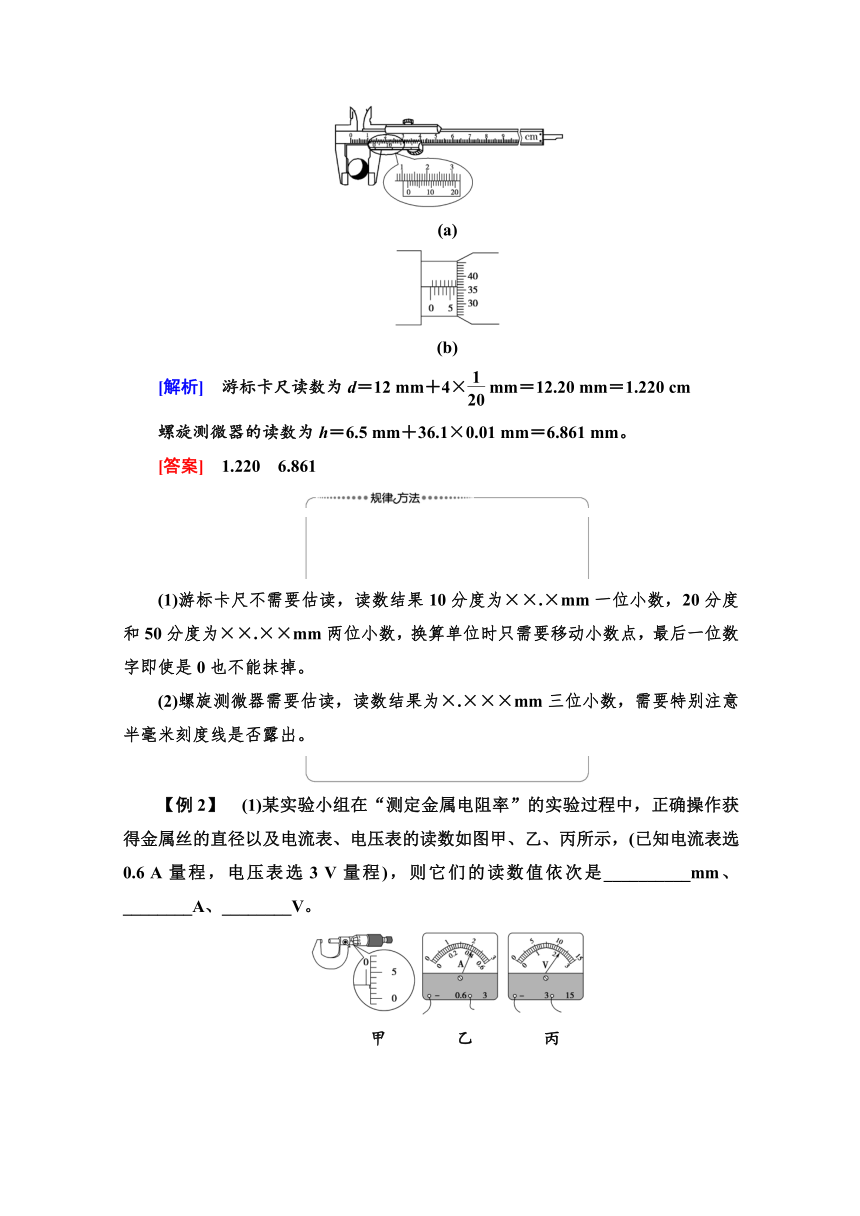
【例1】 某同学利用游标卡尺和螺旋测微器分别测量一圆柱体工件的直径和高度,测量结果如图(a)和(b)所示。该工件的直径为________cm,高度为________mm。
(a)
(b)
[解析] 游标卡尺读数为d=12 mm+4× mm=12.20 mm=1.220 cm
螺旋测微器的读数为h=6.5 mm+36.1×0.01 mm=6.861 mm。
[答案] 1.220 6.861
(1)游标卡尺不需要估读,读数结果10分度为××.×mm一位小数,20分度和50分度为××.××mm两位小数,换算单位时只需要移动小数点,最后一位数字即使是0也不能抹掉。
(2)螺旋测微器需要估读,读数结果为×.×××mm三位小数,需要特别注意半毫米刻度线是否露出。
【例2】 (1)某实验小组在“测定金属电阻率”的实验过程中,正确操作获得金属丝的直径以及电流表、电压表的读数如图甲、乙、丙所示,(已知电流表选0.6 A量程,电压表选3 V量程),则它们的读数值依次是__________mm、________A、________V。
甲 乙 丙
丁
(2)已知实验中所用的电流表内阻约几欧,电压表内阻约20 kΩ,则本实验电路应当采用图丁中的________(选填“A”或“B”),用此电路测量的金属丝电阻比真实值偏________(选填“大”或“小”)。
(3)若测得电流为I、电压为U,金属丝的长度为L,直径为d,则该金属丝的电阻率ρ=________(用题中字母代号表示)。
[解析] (1)螺旋测微器的读数为d=0.5 mm+2.6×0.01 mm=0.526 mm;
电流表的读数为I=0.42 A;
电压表的读数为U=2.25 V;
(2)根据题意,待测电阻阻值远小于电压表内阻,故电流表应用外接法,故电路图A为应当采用的最佳电路。此电路中,由于电压表的分流作用,故测量的金属丝电阻比真实值偏小;
(3)根据欧姆定律R=和金属丝电阻R=ρ解得:ρ=。
[答案] (1)0.526 0.42 2.25 (2)A 小
(3)
【例3】 某同学用伏安法测量导体的电阻,现有量程为3 V、内阻约为3 kΩ的电压表和量程为0.6 A、内阻约为0.1 Ω的电流表。采用分压电路接线,图甲是实物的部分连线图,待测电阻为图乙中的R1,其阻值约为5 Ω。
甲 乙
(1)测R1阻值的最优连接方式为导线①连接________(选填a或b)、导线②连接________(选填c或d)。
(2)正确接线测得实验数据如表,用作图法求得R1的阻值为________Ω。
U/V 0.40 0.80 1.20 1.60 2.00 2.40
I/A 0.09 0.19 0.27 0.35 0.44 0.53
(3)已知图乙中R2与R1是材料相同、厚度相等、表面为正方形的两导体,R2的边长是R1的,若测R2的阻值,则最优的连线应选________(填选项)。
A.①连接a,②连接c
B.①连接a,②连接d
C.①连接b,②连接c
D.①连接b,②连接d
[解析] (1)由于实验测量的是一个小电阻,故电流表应外接,因此导线①接a,由于采用分压电路,故导线②应接d。
(2)根据实验数据作出R1的U?I曲线如图所示,图线的斜率即为电阻R1的大小,由图象可知,R1=4.6 Ω。
(3)设R1的边长为l,厚度为h,电阻率为ρ,根据电阻定律,得R1=ρ=,R2的阻值R2=ρ==R1,故测量R2的电路同测量R1的电路,故选项B正确。
[答案] (1)a d (2)作图见解析,4.6(4.4~4.7均可) (3)B
(1)作图象时,应使大多数的点在直线或平滑的曲线上,不在线上的点尽量均匀分布在它们的两侧,误差较大的点舍去不用。
(2)偶然误差与系统误差的关系
①偶然误差:由于各种偶然因素对实验者、测量仪器、被测物理量的影响而产生的。通过多次测量求平均值(或采用图象法处理数据)可减小偶然误差。
②系统误差:由于仪器本身不精密,实验方法粗略或实验原理不完善而产生的。通过校准仪器或改进实验方法和实验设计原理可减小误差。
1.(多选)在“测定金属的电阻率”的实验中,以下操作中错误的是( )
A.用米尺测量金属丝的全长,且测量三次,算出其平均值,然后再将金属丝接入电路中
B.用螺旋测微器在金属丝三个不同部位各测量一次直径,算出其平均值
C.用伏安法测电阻时,采用电流表内接法,多次测量后算出平均值
D.实验中应保持金属丝的温度不变
AC [实验中应测量出金属丝接入电路中的有效长度,而不是全长;金属丝的电阻很小,与电压表内阻相差很大,使金属丝与电压表并联,电压表对它分流作用很小,应采用电流表外接法。故A、C操作错误。]
2.某同学测定一金属杆的长度和直径,示数如图甲、乙所示,则该金属杆的长度和直径分别为________cm和________mm。
甲
乙
[解析] 金属杆长度由刻度尺示数可得,由题图甲得L=60.10 cm。由题图乙知,此游标尺为50分度,游标尺上第10刻线与主尺上一刻线对齐,则金属杆直径为d=4 mm+×10 mm=4.20 mm。
[答案] 60.10 4.20
3.(1)如图甲、乙所示的两把游标卡尺,它们的游标尺分别为9 mm长10等分、19 mm长20等分,则读数依次为________mm、________mm。
甲 乙
(2)使用螺旋测微器测量金属丝的直径,示数如图所示,则金属丝的直径是________mm。
[解析] (1)题图甲读数:整毫米是17,不足1毫米数是5×0.1 mm=0.5 mm,最后结果是17 mm+0.5 mm=17.5 mm。
题图乙读数:整毫米是23,不足1毫米数是7×0.05 mm=0.35 mm,最后结果是23 mm+0.35 mm=23.35 mm。
(2)固定刻度示数为2.0 mm,不足半毫米的从可动刻度上读,其示数为14.0,最后的读数:2.0 mm+14.0×0.01 mm=2.140 mm。
[答案] (1)17.5 23.35 (2)2.140
4.在“测定金属丝的电阻率”的实验中,某同学进行了如下测量:
(1)用毫米刻度尺测量接入电路中的被测金属丝的有效长度。测量3次,求出其平均值l。其中一次测量结果如图甲所示,金属丝的另一端与刻度尺的零刻线对齐,图中读数为________cm。用螺旋测微器测量金属丝的直径,选不同的位置测量3次,求出其平均值D。其中一次测量结果如图乙所示,图中读数为________mm。
甲 乙
(2)采用如图所示的电路测量金属丝的电阻。电阻的测量值比真实值________(选填“偏大”或“偏小”)。最后由公式ρ=________计算出金属丝的电阻率(用直接测量的物理量表示)。
(3)请你根据电路图在实物图中进行实物连线。(电流表选0.6 A量程,电压表选3 V量程)
[解析] (1)金属丝的长度为24.12~24.14 cm
直径读数为0.515~0.518 mm。
(2)采用安培表外接法,由于电压表的内阻不是无穷大,电压表有分流,从而电流表的测量值大于真实值,由R=可知,电阻的测量值小于真实值。
由R=ρ,R=,S=πd2,可得ρ=。
(3)实物连接如图所示。
[答案] (1)24.12 ~24.14 0.515~0.518 (2)偏小 (3)见解析图
5.某同学测量一金属导体的电阻率,如图甲所示,该导体横截面为空心的正方形。外正方形的边长是内正方形边长的2倍且内正方形中空。经粗略测量该金属导体电阻为5 Ω左右。为了精确测量它的阻值R,以便进一步测出该材料的电阻率ρ,实验室备有下列器材。
A.电源E(电动势为3 V,内阻不计)
B.电流表A1(量程为0~1 A,内阻r1约为0.1 Ω)
C.电流表A2(量程为0~0.6 A,内阻r2=5 Ω)
D.滑动变阻器R0(阻值范围0~3 Ω)
E.开关S,导线若干
甲 乙
(1)请在图乙虚线框内补充画出完整、合理的测量电路图。
(2)做实验时,先把滑动变阻器滑片P滑动到A端,闭合开关S,滑动P到合适位置,记录电流表A1的读数I1,记录电流表A2的读数I2,可以求出金属导体电阻R=________(用题中所给字母表示),然后滑动滑片,多次测量求平均值,可得到更精确阻值。
(3)该同学测得外正方形的边长为a,金属导体的长度为L。用已经测得的物理量I1、I2、L、a及题中所给物理量可得到该金属材料电阻率的表达式为ρ=________。
[解析] (1)电路图如图所示。
(2)由并联知识和电阻定义式可知R=。
(3)该导体横截面积为S=a2-=a2
由电阻定律R=ρ
可得ρ=。
[答案] (1)见解析 (2) (3)
实验步骤
1.直径测定
用螺旋测微器在被测金属导线上的三个不同位置各测一次直径,求出其平均值d,计算出导线的横截面积S=。
2.电路连接
按如图所示的原理电路图连接好用伏安法测电阻的实验电路。
3.长度测量
用毫米刻度尺测量接入电路中的被测金属导线的有效长度,反复测量3次,求出其平均值l。
4.U、I测量
把滑动变阻器的滑动片调节到使接入电路中的电阻值最大的位置,电路经检查确认无误后,闭合开关S,改变滑动变阻器滑动片的位置,读出几组相应的电流表、电压表的示数I和U的值,记入表格内,断开开关S。
5.拆去实验线路,整理好实验器材。
五、数据处理
1.在求Rx的平均值时可用两种方法
(1)用Rx=分别算出各次的数值,再取平均值。
(2)用U?I图线的斜率求出。
2.计算电阻率
将记录的数据Rx、l、d的值代入电阻率计算式ρ=Rx=。
六、误差分析
1.金属丝的横截面积是利用直径计算而得,直径的测量是产生误差的主要来源之一。
2.采用伏安法测量金属丝的电阻时,由于采用的是电流表外接法,测量值小于真实值,使电阻率的测量值偏小。
3.金属丝的长度测量、电流表和电压表的读数等会带来偶然误差。
4.由于金属丝通电后发热升温,会使金属丝的电阻率变大,造成测量误差。
七、注意事项
1.本实验中被测金属导线的电阻值较小,因此实验电路一般采用电流表外接法。
2.实验连线时,应先从电源的正极出发,依次将电源、开关、电流表、待测金属导线、滑动变阻器连成主干线路,然后再把电压表并联在待测金属导线的两端。
3.测量被测金属导线的有效长度,是指测量待测导线接入电路的两个端点之间的长度,亦即电压表两端点间的待测导线长度,测量时应将导线拉直,反复测量三次,求其平均值。
4.测金属导线直径一定要选三个不同部位进行测量,求其平均值。
5.闭合开关S之前,一定要使滑动变阻器的滑片处在有效电阻值最大的位置。
6.在用伏安法测电阻时,通过待测导线的电流强度I不宜过大(电流表用0~0.6 A量程),通电时间不宜过长,以免金属导线的温度明显升高,造成其电阻率在实验过程中逐渐增大。
7.求Rx的平均值时可用两种方法:第一种是用Rx=算出各次的测量值,再取平均值;第二种是用图象(U?I图线)来求出。若采用图象法,在描点时,要尽量使各点间的距离拉大一些,连线时要尽可能地让各点均匀分布在直线的两侧,个别明显偏离较远的点可以不予考虑。
【例1】 某同学利用游标卡尺和螺旋测微器分别测量一圆柱体工件的直径和高度,测量结果如图(a)和(b)所示。该工件的直径为________cm,高度为________mm。
(a)
(b)
[解析] 游标卡尺读数为d=12 mm+4× mm=12.20 mm=1.220 cm
螺旋测微器的读数为h=6.5 mm+36.1×0.01 mm=6.861 mm。
[答案] 1.220 6.861
(1)游标卡尺不需要估读,读数结果10分度为××.×mm一位小数,20分度和50分度为××.××mm两位小数,换算单位时只需要移动小数点,最后一位数字即使是0也不能抹掉。
(2)螺旋测微器需要估读,读数结果为×.×××mm三位小数,需要特别注意半毫米刻度线是否露出。
【例2】 (1)某实验小组在“测定金属电阻率”的实验过程中,正确操作获得金属丝的直径以及电流表、电压表的读数如图甲、乙、丙所示,(已知电流表选0.6 A量程,电压表选3 V量程),则它们的读数值依次是__________mm、________A、________V。
甲 乙 丙
丁
(2)已知实验中所用的电流表内阻约几欧,电压表内阻约20 kΩ,则本实验电路应当采用图丁中的________(选填“A”或“B”),用此电路测量的金属丝电阻比真实值偏________(选填“大”或“小”)。
(3)若测得电流为I、电压为U,金属丝的长度为L,直径为d,则该金属丝的电阻率ρ=________(用题中字母代号表示)。
[解析] (1)螺旋测微器的读数为d=0.5 mm+2.6×0.01 mm=0.526 mm;
电流表的读数为I=0.42 A;
电压表的读数为U=2.25 V;
(2)根据题意,待测电阻阻值远小于电压表内阻,故电流表应用外接法,故电路图A为应当采用的最佳电路。此电路中,由于电压表的分流作用,故测量的金属丝电阻比真实值偏小;
(3)根据欧姆定律R=和金属丝电阻R=ρ解得:ρ=。
[答案] (1)0.526 0.42 2.25 (2)A 小
(3)
【例3】 某同学用伏安法测量导体的电阻,现有量程为3 V、内阻约为3 kΩ的电压表和量程为0.6 A、内阻约为0.1 Ω的电流表。采用分压电路接线,图甲是实物的部分连线图,待测电阻为图乙中的R1,其阻值约为5 Ω。
甲 乙
(1)测R1阻值的最优连接方式为导线①连接________(选填a或b)、导线②连接________(选填c或d)。
(2)正确接线测得实验数据如表,用作图法求得R1的阻值为________Ω。
U/V 0.40 0.80 1.20 1.60 2.00 2.40
I/A 0.09 0.19 0.27 0.35 0.44 0.53
(3)已知图乙中R2与R1是材料相同、厚度相等、表面为正方形的两导体,R2的边长是R1的,若测R2的阻值,则最优的连线应选________(填选项)。
A.①连接a,②连接c
B.①连接a,②连接d
C.①连接b,②连接c
D.①连接b,②连接d
[解析] (1)由于实验测量的是一个小电阻,故电流表应外接,因此导线①接a,由于采用分压电路,故导线②应接d。
(2)根据实验数据作出R1的U?I曲线如图所示,图线的斜率即为电阻R1的大小,由图象可知,R1=4.6 Ω。
(3)设R1的边长为l,厚度为h,电阻率为ρ,根据电阻定律,得R1=ρ=,R2的阻值R2=ρ==R1,故测量R2的电路同测量R1的电路,故选项B正确。
[答案] (1)a d (2)作图见解析,4.6(4.4~4.7均可) (3)B
(1)作图象时,应使大多数的点在直线或平滑的曲线上,不在线上的点尽量均匀分布在它们的两侧,误差较大的点舍去不用。
(2)偶然误差与系统误差的关系
①偶然误差:由于各种偶然因素对实验者、测量仪器、被测物理量的影响而产生的。通过多次测量求平均值(或采用图象法处理数据)可减小偶然误差。
②系统误差:由于仪器本身不精密,实验方法粗略或实验原理不完善而产生的。通过校准仪器或改进实验方法和实验设计原理可减小误差。
1.(多选)在“测定金属的电阻率”的实验中,以下操作中错误的是( )
A.用米尺测量金属丝的全长,且测量三次,算出其平均值,然后再将金属丝接入电路中
B.用螺旋测微器在金属丝三个不同部位各测量一次直径,算出其平均值
C.用伏安法测电阻时,采用电流表内接法,多次测量后算出平均值
D.实验中应保持金属丝的温度不变
AC [实验中应测量出金属丝接入电路中的有效长度,而不是全长;金属丝的电阻很小,与电压表内阻相差很大,使金属丝与电压表并联,电压表对它分流作用很小,应采用电流表外接法。故A、C操作错误。]
2.某同学测定一金属杆的长度和直径,示数如图甲、乙所示,则该金属杆的长度和直径分别为________cm和________mm。
甲
乙
[解析] 金属杆长度由刻度尺示数可得,由题图甲得L=60.10 cm。由题图乙知,此游标尺为50分度,游标尺上第10刻线与主尺上一刻线对齐,则金属杆直径为d=4 mm+×10 mm=4.20 mm。
[答案] 60.10 4.20
3.(1)如图甲、乙所示的两把游标卡尺,它们的游标尺分别为9 mm长10等分、19 mm长20等分,则读数依次为________mm、________mm。
甲 乙
(2)使用螺旋测微器测量金属丝的直径,示数如图所示,则金属丝的直径是________mm。
[解析] (1)题图甲读数:整毫米是17,不足1毫米数是5×0.1 mm=0.5 mm,最后结果是17 mm+0.5 mm=17.5 mm。
题图乙读数:整毫米是23,不足1毫米数是7×0.05 mm=0.35 mm,最后结果是23 mm+0.35 mm=23.35 mm。
(2)固定刻度示数为2.0 mm,不足半毫米的从可动刻度上读,其示数为14.0,最后的读数:2.0 mm+14.0×0.01 mm=2.140 mm。
[答案] (1)17.5 23.35 (2)2.140
4.在“测定金属丝的电阻率”的实验中,某同学进行了如下测量:
(1)用毫米刻度尺测量接入电路中的被测金属丝的有效长度。测量3次,求出其平均值l。其中一次测量结果如图甲所示,金属丝的另一端与刻度尺的零刻线对齐,图中读数为________cm。用螺旋测微器测量金属丝的直径,选不同的位置测量3次,求出其平均值D。其中一次测量结果如图乙所示,图中读数为________mm。
甲 乙
(2)采用如图所示的电路测量金属丝的电阻。电阻的测量值比真实值________(选填“偏大”或“偏小”)。最后由公式ρ=________计算出金属丝的电阻率(用直接测量的物理量表示)。
(3)请你根据电路图在实物图中进行实物连线。(电流表选0.6 A量程,电压表选3 V量程)
[解析] (1)金属丝的长度为24.12~24.14 cm
直径读数为0.515~0.518 mm。
(2)采用安培表外接法,由于电压表的内阻不是无穷大,电压表有分流,从而电流表的测量值大于真实值,由R=可知,电阻的测量值小于真实值。
由R=ρ,R=,S=πd2,可得ρ=。
(3)实物连接如图所示。
[答案] (1)24.12 ~24.14 0.515~0.518 (2)偏小 (3)见解析图
5.某同学测量一金属导体的电阻率,如图甲所示,该导体横截面为空心的正方形。外正方形的边长是内正方形边长的2倍且内正方形中空。经粗略测量该金属导体电阻为5 Ω左右。为了精确测量它的阻值R,以便进一步测出该材料的电阻率ρ,实验室备有下列器材。
A.电源E(电动势为3 V,内阻不计)
B.电流表A1(量程为0~1 A,内阻r1约为0.1 Ω)
C.电流表A2(量程为0~0.6 A,内阻r2=5 Ω)
D.滑动变阻器R0(阻值范围0~3 Ω)
E.开关S,导线若干
甲 乙
(1)请在图乙虚线框内补充画出完整、合理的测量电路图。
(2)做实验时,先把滑动变阻器滑片P滑动到A端,闭合开关S,滑动P到合适位置,记录电流表A1的读数I1,记录电流表A2的读数I2,可以求出金属导体电阻R=________(用题中所给字母表示),然后滑动滑片,多次测量求平均值,可得到更精确阻值。
(3)该同学测得外正方形的边长为a,金属导体的长度为L。用已经测得的物理量I1、I2、L、a及题中所给物理量可得到该金属材料电阻率的表达式为ρ=________。
[解析] (1)电路图如图所示。
(2)由并联知识和电阻定义式可知R=。
(3)该导体横截面积为S=a2-=a2
由电阻定律R=ρ
可得ρ=。
[答案] (1)见解析 (2) (3)
