湘教版八年级上册 数学 课件 :2.4 线段的垂直平分线1(18张)
文档属性
| 名称 | 湘教版八年级上册 数学 课件 :2.4 线段的垂直平分线1(18张) |

|
|
| 格式 | zip | ||
| 文件大小 | 503.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览





文档简介
(共18张PPT)
2.4
线段的垂直平分线
A
B
L
实际问题
在107国道的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得该医院到两个工厂的距离相等,问医院的院址应选在何处?
107
国道
C
动手操作
A
B
直线l
垂直且平分一条线段的直线叫做这条线段的
垂直平分线
C
l⊥AB,AC=BC
新知引入
A
B
P1
P
l
C
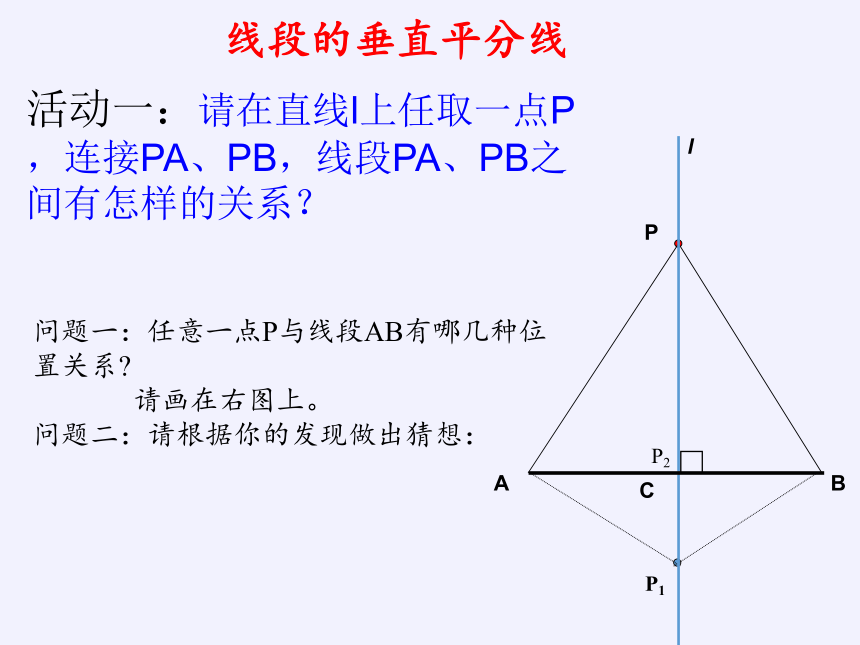
活动一:请在直线l上任取一点P,连接PA、PB,线段PA、PB之间有怎样的关系?
P2
问题一:任意一点P与线段AB有哪几种位置关系?
请画在右图上。
问题二:请根据你的发现做出猜想:
线段的垂直平分线
性质定理:线段垂直平分线上的点到线段两端的距离相等。
线段的垂直平分线
A
B
P
l
C
点P到线段AB两端的距离相等
点P在线段AB的垂直平分线上
性质定理
几何语言
∵点P在线段AB的垂直平分线l上
∴PA=PB
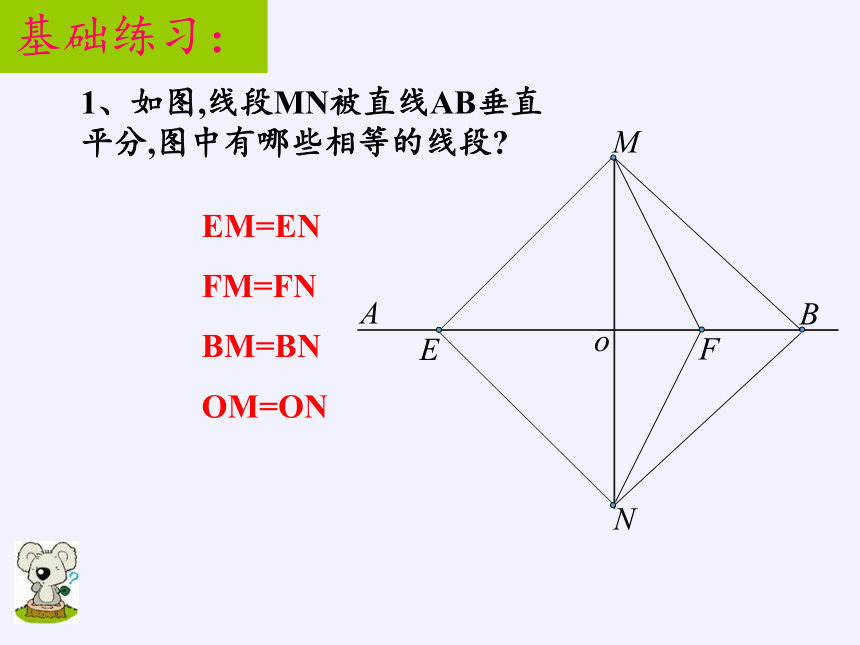
1、如图,线段MN被直线AB垂直平分,图中有哪些相等的线段?
基础练习:
EM=EN
FM=FN
BM=BN
OM=ON
2、如图所示,在ΔABC中,边BC的垂直平分线MN分别交AB于点M,交BC于点N,
ΔBMC的周长为23,且BM=7,求BC的长。
C
B
M
N
A
解:∵
MN是线段BC的垂直平分线
BM=7
∴
CM=BM=7
∵
CΔBMC
=23
∴BM+CM+BC=23
∴BC=23-CM-BM
=23-7-7
=9
基础练习:
107国道
A
B
生活中的数学
线段的垂直平分线
A
B
P
性质定理:线段垂直平分线上的点到线段两端的距离相等。
点P到线段AB两端的距离相等
点P在线段AB的垂直平分线上
到线段两端距离相等的点在线段的垂直平分线上。
性质定理
?
逆命题:
P1
到线段两端距离相等的点在线段的垂直平分线上。
逆命题
证明
已知:如图,PA=PB
求证:点P在线段AB的垂直平分线上
证明:
∵PA=PB
∴△PAB是等腰三角形
又∵PC⊥AB
∴PC是底边AB上的高,也是底边AB上的中线
∴PC⊥AB且AC=BC
∴PC是线段AB的垂直平分线
∴点P在线段AB的垂直平分线上
定理
A
B
P
l
C
过点P作直线l垂直于线段AB并交于点C
逆定理:到线段两端距离相等的点在线段的垂直平分线上。
线段的垂直平分线
性质定理:线段垂直平分线上的点到线段两端的距离相等。
点P到线段AB两端的距离相等
点P在线段AB的垂直平分线上
逆定理
性质定理
结论:三角形三边的垂直平分线交于一点,这一点到三角形三个顶点的距离相等。
用心想一想,马到功成
例1已知:在△ABC中,设AB、BC的垂直平分线交于点P
求证:P点在AC的垂直平分线上.
证明:
∵点P在线段AB的垂直平分线上,
∴PA=PB.
同理PB=PC.∴PA=PC.
∴P点在AC的垂直平分线上.
http://www.bnup.com.cn
A
P
C
B
连接AP,BP,CP.
∴AB、BC、AC的垂直平分线相交于点P
·
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
思考:生活中的数学
本节课学习了什么内容?
逆定理:到线段两端距离相等的点在线段的垂直平分线上。
线段的垂直平分线
性质定理:线段垂直平分线上的点到线段两端的距离相等。
点P到线段AB两端的距离相等
点P在线段AB的垂直平分线上
逆定理
性质定理
作业
1、必做作业:
(1)课本:P
70练习1、2题
2、选做作业:借助直尺、三角板画出直角三角形,锐角三角形,钝角三角形三边的垂直平分线,并观察垂直平分线交点的位置。
谢
谢
2.4
线段的垂直平分线
A
B
L
实际问题
在107国道的同侧,有两个化工厂A、B,为了便于两厂的工人看病,市政府计划在公路边上修建一所医院,使得该医院到两个工厂的距离相等,问医院的院址应选在何处?
107
国道
C
动手操作
A
B
直线l
垂直且平分一条线段的直线叫做这条线段的
垂直平分线
C
l⊥AB,AC=BC
新知引入
A
B
P1
P
l
C
活动一:请在直线l上任取一点P,连接PA、PB,线段PA、PB之间有怎样的关系?
P2
问题一:任意一点P与线段AB有哪几种位置关系?
请画在右图上。
问题二:请根据你的发现做出猜想:
线段的垂直平分线
性质定理:线段垂直平分线上的点到线段两端的距离相等。
线段的垂直平分线
A
B
P
l
C
点P到线段AB两端的距离相等
点P在线段AB的垂直平分线上
性质定理
几何语言
∵点P在线段AB的垂直平分线l上
∴PA=PB
1、如图,线段MN被直线AB垂直平分,图中有哪些相等的线段?
基础练习:
EM=EN
FM=FN
BM=BN
OM=ON
2、如图所示,在ΔABC中,边BC的垂直平分线MN分别交AB于点M,交BC于点N,
ΔBMC的周长为23,且BM=7,求BC的长。
C
B
M
N
A
解:∵
MN是线段BC的垂直平分线
BM=7
∴
CM=BM=7
∵
CΔBMC
=23
∴BM+CM+BC=23
∴BC=23-CM-BM
=23-7-7
=9
基础练习:
107国道
A
B
生活中的数学
线段的垂直平分线
A
B
P
性质定理:线段垂直平分线上的点到线段两端的距离相等。
点P到线段AB两端的距离相等
点P在线段AB的垂直平分线上
到线段两端距离相等的点在线段的垂直平分线上。
性质定理
?
逆命题:
P1
到线段两端距离相等的点在线段的垂直平分线上。
逆命题
证明
已知:如图,PA=PB
求证:点P在线段AB的垂直平分线上
证明:
∵PA=PB
∴△PAB是等腰三角形
又∵PC⊥AB
∴PC是底边AB上的高,也是底边AB上的中线
∴PC⊥AB且AC=BC
∴PC是线段AB的垂直平分线
∴点P在线段AB的垂直平分线上
定理
A
B
P
l
C
过点P作直线l垂直于线段AB并交于点C
逆定理:到线段两端距离相等的点在线段的垂直平分线上。
线段的垂直平分线
性质定理:线段垂直平分线上的点到线段两端的距离相等。
点P到线段AB两端的距离相等
点P在线段AB的垂直平分线上
逆定理
性质定理
结论:三角形三边的垂直平分线交于一点,这一点到三角形三个顶点的距离相等。
用心想一想,马到功成
例1已知:在△ABC中,设AB、BC的垂直平分线交于点P
求证:P点在AC的垂直平分线上.
证明:
∵点P在线段AB的垂直平分线上,
∴PA=PB.
同理PB=PC.∴PA=PC.
∴P点在AC的垂直平分线上.
http://www.bnup.com.cn
A
P
C
B
连接AP,BP,CP.
∴AB、BC、AC的垂直平分线相交于点P
·
某区政府为了方便居民的生活,计划在三个住宅小区A、B、C之间修建一个购物中心,试问,该购物中心应建于何处,才能使得它到三个小区的距离相等。
A
B
C
思考:生活中的数学
本节课学习了什么内容?
逆定理:到线段两端距离相等的点在线段的垂直平分线上。
线段的垂直平分线
性质定理:线段垂直平分线上的点到线段两端的距离相等。
点P到线段AB两端的距离相等
点P在线段AB的垂直平分线上
逆定理
性质定理
作业
1、必做作业:
(1)课本:P
70练习1、2题
2、选做作业:借助直尺、三角板画出直角三角形,锐角三角形,钝角三角形三边的垂直平分线,并观察垂直平分线交点的位置。
谢
谢
同课章节目录
