人教版七年级数学上册第二章 整式的加减 复习小结课件(32张)
文档属性
| 名称 | 人教版七年级数学上册第二章 整式的加减 复习小结课件(32张) |

|
|
| 格式 | zip | ||
| 文件大小 | 489.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
第二章整式的加减复习小结
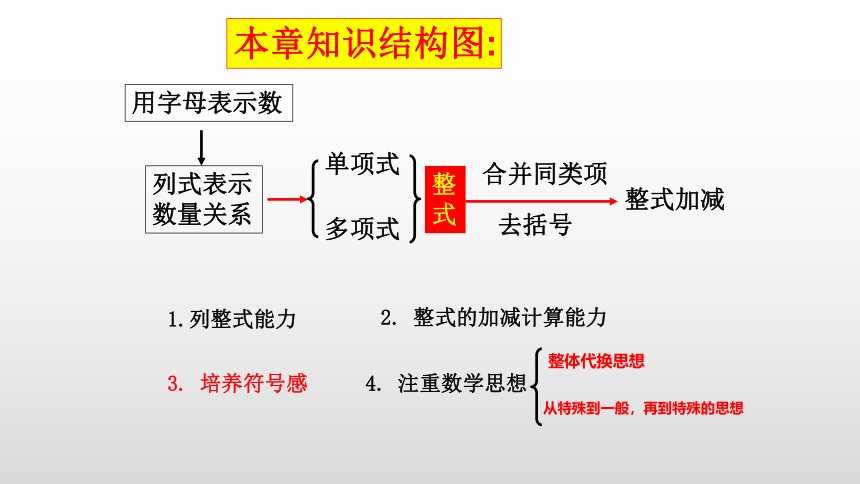
用字母表示数
列式表示数量关系
单项式
多项式
整式
整式加减
合并同类项
去括号
本章知识结构图:
1.列整式能力
2.
整式的加减计算能力
3.
培养符号感
4.
注重数学思想
整体代换思想
从特殊到一般,再到特殊的思想
次数:
所有字母的指数的和。
系数:单项式中的数字因数。
项:式中的每个单项式叫多项式的项。
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数。
整式
注意:
1、多项式的次数为最高次项的次数.
2、多项式的每一项都包括它前面的符号.
知识点1:
单独的一个数字或字母也是单项式.
1
用字母表示数
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
(1)某种商品每袋4.8元,在一个月内的销售量是m
袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是
r,h,用式子表示圆柱体的体积.
(3)有两片棉田,一片有m
hm2
(公顷,1
hm2
=104
m2
),平均每公顷产棉花a
kg;另一片有n
hm2
,平均每公顷产棉花b
kg,用式子表示两片棉田上棉花的总产量.
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a
mm,小正方形的边长是b
mm,用式子表示剩余部分的面积.
练一练
(1)5箱苹果重m
kg,每箱重
kg
;
(2)一个数比a的2倍小5,则这个数为
;
(3)全校学生总数是x,其中女生占总数52%,则女生人数是
,男生人数是
;
(4)某班有a名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共
本;
2
用式子表示下列数量
数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示字母与数字、字母与字母的积).
这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
例如:像-2,a,-b,
等是单项式.
注意:像
,
,
等不是单项式.
2
单项式
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法
注意
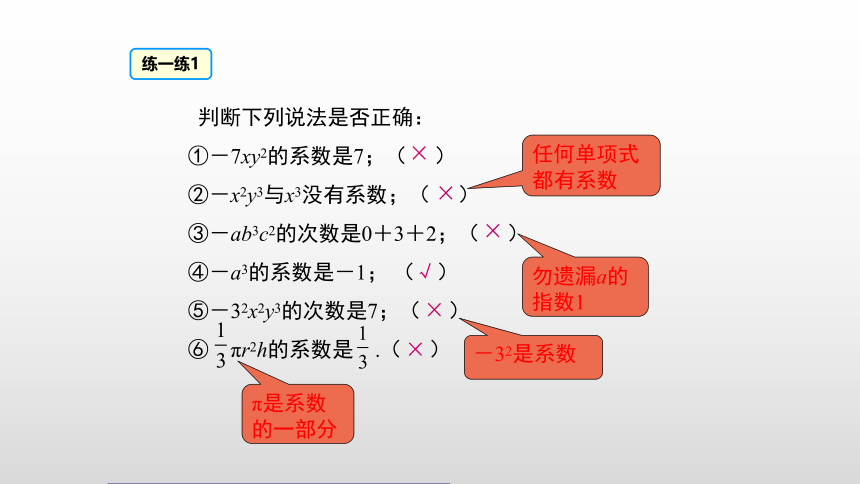
练一练1
判断下列说法是否正确:
①-7xy2的系数是7;(
)
②-x2y3与x3没有系数;(
)
③-ab3c2的次数是0+3+2;(
)
④-a3的系数是-1;
(
)
⑤-32x2y3的次数是7;(
)
⑥
πr2h的系数是
.(
)
×
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
任何单项式都有系数
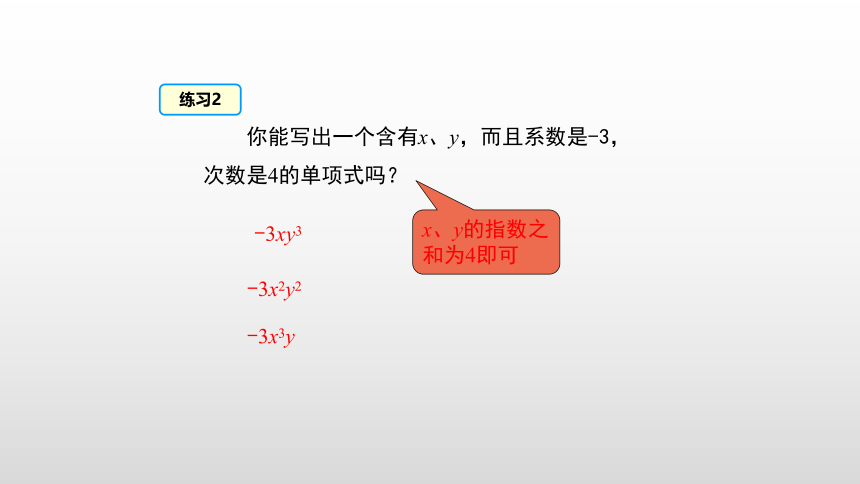
你能写出一个含有x、y,而且系数是-3,次数是4的单项式吗?
-3xy3
-3x2y2
-3x3y
练习2
x、y的指数之和为4即可
3
若
是关于
x,y
的一个四次单项式,m,n应满足的条件?
单项式次数是2+n
所以m≠
2,n=2.
2+n=4,
m-2
≠
0,
为什么?
解:m,n要满足
几个单项式的和叫做多项式
单项式
单项式
+
判断.
下列代数式哪些是多项式?
单项式和多项式通称整式
3
多项式
X+Y
a2+b-3c
ab-
r2
X4+2x2Y3+18
1
2
练习1
下列多项式的项分别是什么
项
X、Y
a2、b、-3c
X4、2X2Y3、18
多项式的次数。
次数
1次
2次
2次
5次
(一次二项式)
(二次三项式)
(二次二项式)
(五次三项式)
找多项式的项时要注意什么
ab、-
r2
1
2
几次
几项式
一般地,多项式里次数最高的项的次数,
就是这个
2.下列说法中,正确的是(
)
D
4、(1)买单价为a元的笔记本m本,付出20元,应找回_______元.
(20-am)
(2)用字母表示图形中的黑色部分面积是________
a
3
m
m
3a-m2
3、判断题:
(1)-5ab2的系数是5(
)
(2)xy2的系数是0(
)
(3)
的系数是
(
)
(4)-ab2c的次数是2(
)
×
×
×
×
提高探究
已知n是自然数,多项式
y
n+1+3x3-2x
是三次三项式,那么n可以是哪些数?
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
注意:几个常数项也是同类项.
4
合并同类项
两相同:①所含字母相同;
②相同字母的指数相同.
两无关:①与系数无关;
②与字母的顺序无关.
学以致用
(1).若
与
是同类项,m=___,n=___.
(2).若
与
是同类项,m=___,n=___.
(3).若
与
是同类项,m=___,n=___.
(4).若
与
是同类项,m=__,n=___.
学以致用
用下划线的方式找出各多项式中的同类项.
若把(x+y)、(x-y)分别看作一个整体,指出下面式子中的同类项.
2(x+y)+3(x-y)2-5(x+y)-8(x-y)2+(x+y)
合并同类项法则
同类项的系数相加,所得结果作为
系数,字母和字母的指数不变.
一变
二不变
解:
一找
同类项
二结合
三合并
技巧方法
合并同类项
学以致用
求下列各式的值.
拓展提高
合并下面多项式中的同类项.
学以致用
求下列各式的值.
去括号法则
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
典例精析
例1
化简下列各式:
(1)8a+2b+(5a-b);
(2)(5a-3b)-3(a2-2b).
解:(1)8a+2b+(5a-b)
=8a+2b+5a-b
=13a+b;
(2)(5a-3b)-3(a2-2b)
=(5a-3b)-(3a2-6b)
=5a-3b-3a2+6b
=-3a2+5a+3b
(2)5a2
-[a2+(5
a2
-2a)
-2(a2
-3a)]
1、计算:
(1)3(
xy2-x2y)
-2(xy+xy2)+3x2y;
解:1、(1)原式=3
xy2-3x2y-
2xy
-
2xy2
+3x2y
=(3-2)
xy2
+(-3+3)
+3x2y-2xy
=
xy2-
2xy
(2)原式=5a2
-(a2+5
a2
-2a
-2a2+6a)
=
5a2
-
(4a2
+4a)
=
5a2
-
4a2-
4a
=a2
-
4a
2、化简求值:(-4
x2
+2x
-8)
-
(x-2)其中x=
3
计算与求值:
a
0
b
已知数a,b在数轴上的位置如图所示
化简下列式子:
整式与绝对值
第二章整式的加减复习小结
用字母表示数
列式表示数量关系
单项式
多项式
整式
整式加减
合并同类项
去括号
本章知识结构图:
1.列整式能力
2.
整式的加减计算能力
3.
培养符号感
4.
注重数学思想
整体代换思想
从特殊到一般,再到特殊的思想
次数:
所有字母的指数的和。
系数:单项式中的数字因数。
项:式中的每个单项式叫多项式的项。
(其中不含字母的项叫做常数项)
次数:多项式中次数最高的项的次数。
整式
注意:
1、多项式的次数为最高次项的次数.
2、多项式的每一项都包括它前面的符号.
知识点1:
单独的一个数字或字母也是单项式.
1
用字母表示数
列式时:
①数与字母、字母与字母相乘省略乘号;
②数与字母相乘时数字在前;
③式子中出现除法运算时,一般按分数形式来写;
④带分数与字母相乘时,把带分数化成假分数;
⑤带单位时,适当加括号.
(1)某种商品每袋4.8元,在一个月内的销售量是m
袋,用式子表示在这个月内销售这种商品的收入.
(2)圆柱体的底面半径、高分别是
r,h,用式子表示圆柱体的体积.
(3)有两片棉田,一片有m
hm2
(公顷,1
hm2
=104
m2
),平均每公顷产棉花a
kg;另一片有n
hm2
,平均每公顷产棉花b
kg,用式子表示两片棉田上棉花的总产量.
(4)在一个大正方形铁片中挖去一个小正方形铁片,大正方形的边长是a
mm,小正方形的边长是b
mm,用式子表示剩余部分的面积.
练一练
(1)5箱苹果重m
kg,每箱重
kg
;
(2)一个数比a的2倍小5,则这个数为
;
(3)全校学生总数是x,其中女生占总数52%,则女生人数是
,男生人数是
;
(4)某班有a名学生,现把一批图书分给全班学生阅读,如果每人分4本,还缺25本,则这批图书共
本;
2
用式子表示下列数量
数字和字母之间,字母与字母之间的运算都是乘法运算(都是表示字母与数字、字母与字母的积).
这样的式子叫做单项式,单独的一个数或一个字母也是单项式.
例如:像-2,a,-b,
等是单项式.
注意:像
,
,
等不是单项式.
2
单项式
1.单独一个数或一个字母也是单项式.
2.不含加减运算,单项式只含有乘积运算.
3.单项式数字因数与字母可能一个或多个.
4.可以含有除以数的运算,不能含有除以字母的运算.
判断单项式的方法
注意
练一练1
判断下列说法是否正确:
①-7xy2的系数是7;(
)
②-x2y3与x3没有系数;(
)
③-ab3c2的次数是0+3+2;(
)
④-a3的系数是-1;
(
)
⑤-32x2y3的次数是7;(
)
⑥
πr2h的系数是
.(
)
×
×
×
×
×
√
π是系数的一部分
-32是系数
勿遗漏a的指数1
任何单项式都有系数
你能写出一个含有x、y,而且系数是-3,次数是4的单项式吗?
-3xy3
-3x2y2
-3x3y
练习2
x、y的指数之和为4即可
3
若
是关于
x,y
的一个四次单项式,m,n应满足的条件?
单项式次数是2+n
所以m≠
2,n=2.
2+n=4,
m-2
≠
0,
为什么?
解:m,n要满足
几个单项式的和叫做多项式
单项式
单项式
+
判断.
下列代数式哪些是多项式?
单项式和多项式通称整式
3
多项式
X+Y
a2+b-3c
ab-
r2
X4+2x2Y3+18
1
2
练习1
下列多项式的项分别是什么
项
X、Y
a2、b、-3c
X4、2X2Y3、18
多项式的次数。
次数
1次
2次
2次
5次
(一次二项式)
(二次三项式)
(二次二项式)
(五次三项式)
找多项式的项时要注意什么
ab、-
r2
1
2
几次
几项式
一般地,多项式里次数最高的项的次数,
就是这个
2.下列说法中,正确的是(
)
D
4、(1)买单价为a元的笔记本m本,付出20元,应找回_______元.
(20-am)
(2)用字母表示图形中的黑色部分面积是________
a
3
m
m
3a-m2
3、判断题:
(1)-5ab2的系数是5(
)
(2)xy2的系数是0(
)
(3)
的系数是
(
)
(4)-ab2c的次数是2(
)
×
×
×
×
提高探究
已知n是自然数,多项式
y
n+1+3x3-2x
是三次三项式,那么n可以是哪些数?
所含字母相同,并且相同字母的指数也相同的项叫做同类项.
注意:几个常数项也是同类项.
4
合并同类项
两相同:①所含字母相同;
②相同字母的指数相同.
两无关:①与系数无关;
②与字母的顺序无关.
学以致用
(1).若
与
是同类项,m=___,n=___.
(2).若
与
是同类项,m=___,n=___.
(3).若
与
是同类项,m=___,n=___.
(4).若
与
是同类项,m=__,n=___.
学以致用
用下划线的方式找出各多项式中的同类项.
若把(x+y)、(x-y)分别看作一个整体,指出下面式子中的同类项.
2(x+y)+3(x-y)2-5(x+y)-8(x-y)2+(x+y)
合并同类项法则
同类项的系数相加,所得结果作为
系数,字母和字母的指数不变.
一变
二不变
解:
一找
同类项
二结合
三合并
技巧方法
合并同类项
学以致用
求下列各式的值.
拓展提高
合并下面多项式中的同类项.
学以致用
求下列各式的值.
去括号法则
1.如果括号外的因数是正数,去括号后原括号内各项的符号与原来的符号相同;
2.如果括号外的因数是负数,去括号后原括号内各项的符号与原来的符号相反.
典例精析
例1
化简下列各式:
(1)8a+2b+(5a-b);
(2)(5a-3b)-3(a2-2b).
解:(1)8a+2b+(5a-b)
=8a+2b+5a-b
=13a+b;
(2)(5a-3b)-3(a2-2b)
=(5a-3b)-(3a2-6b)
=5a-3b-3a2+6b
=-3a2+5a+3b
(2)5a2
-[a2+(5
a2
-2a)
-2(a2
-3a)]
1、计算:
(1)3(
xy2-x2y)
-2(xy+xy2)+3x2y;
解:1、(1)原式=3
xy2-3x2y-
2xy
-
2xy2
+3x2y
=(3-2)
xy2
+(-3+3)
+3x2y-2xy
=
xy2-
2xy
(2)原式=5a2
-(a2+5
a2
-2a
-2a2+6a)
=
5a2
-
(4a2
+4a)
=
5a2
-
4a2-
4a
=a2
-
4a
2、化简求值:(-4
x2
+2x
-8)
-
(x-2)其中x=
3
计算与求值:
a
0
b
已知数a,b在数轴上的位置如图所示
化简下列式子:
整式与绝对值
