北师大版九年级上册数学《相似三角形判定定理的证明》当堂达标试题((Word版 含答案)
文档属性
| 名称 | 北师大版九年级上册数学《相似三角形判定定理的证明》当堂达标试题((Word版 含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 307.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 00:00:00 | ||
图片预览



文档简介
北师大版九年级上册数学《相似三角形判定定理的证明》当堂达标试题
知识点回顾:
相似三角形判定定理的证明
相似三角形判定定理的证明的依据:
①
的定义;
②平行线分线段成比例定理.?
2.相似三角形判定定理的证明的思路:添加
线,证明三角形相似.?
达标检测:
1.如图,下列条件不能判定△ADB∽△ABC的是
(
)
A.∠ABD=∠ACB
B.∠ADB=∠ABC
C.AB2=AD·AC
D.=
2.
如图,在△ABC中,点D,E分别是AB,AC边上的点,DE∥BC,AD=2,AB=3,DE=4,则BC等于(
)
A.5
B.6
C.7
D.8
3.
如图,在?ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是
(
)
A.=
B.=
C.=
D.=
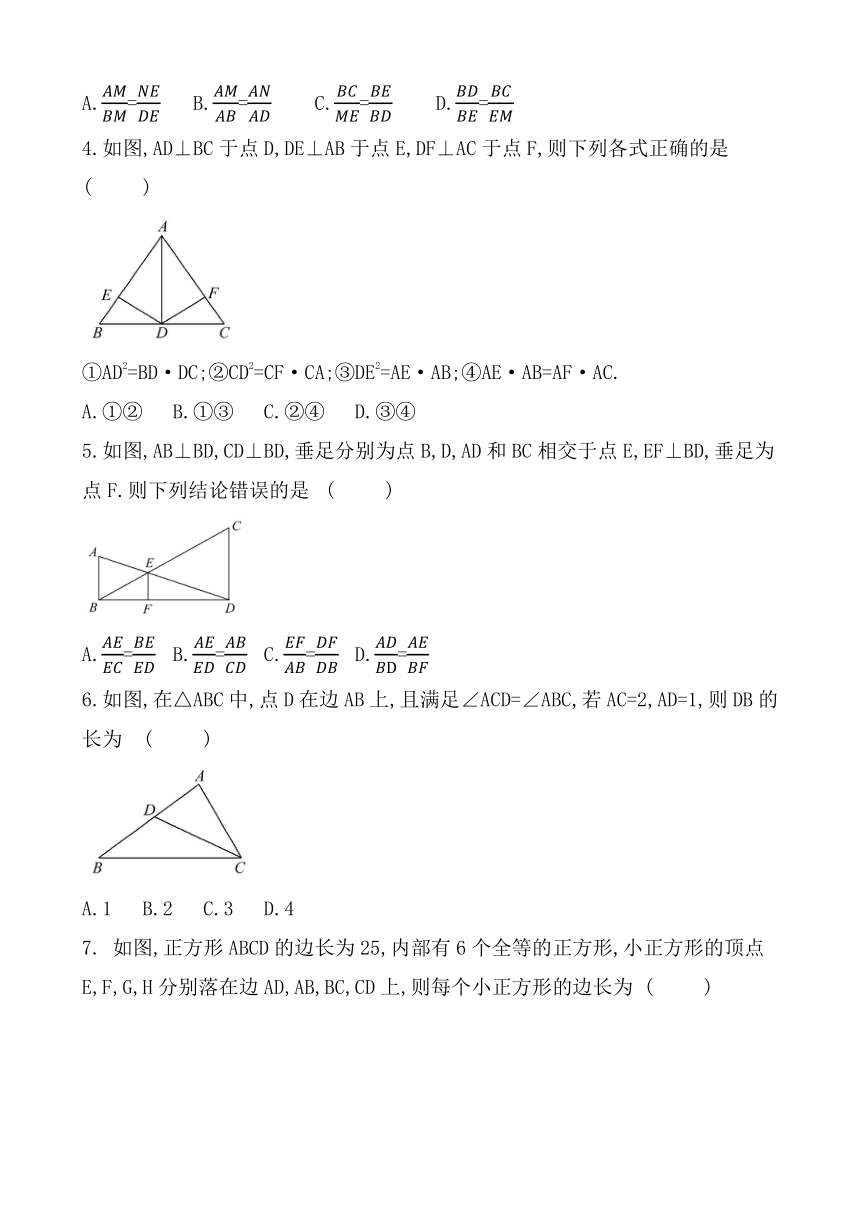
4.如图,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,则下列各式正确的是(
)
①AD2=BD·DC;②CD2=CF·CA;③DE2=AE·AB;④AE·AB=AF·AC.
A.①②
B.①③
C.②④
D.③④
5.如图,AB⊥BD,CD⊥BD,垂足分别为点B,D,AD和BC相交于点E,EF⊥BD,垂足为点F.则下列结论错误的是
(
)
A.=
B.=
C.=
D.=
6.如图,在△ABC中,点D在边AB上,且满足∠ACD=∠ABC,若AC=2,AD=1,则DB的长为
(
)
A.1
B.2
C.3
D.4
7.
如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E,F,G,H分别落在边AD,AB,BC,CD上,则每个小正方形的边长为
(
)
A.6
B.5
C.2
D.
8.如图,在菱形ABCD中,点E是BC的中点,DE与AC交于点F,若AB=6,∠B=60°,则AF的长为
(
)
A.3
B.3.5
C.3
D.4
9.如图,在菱形ABCD中,E是BC边上的点,连接AE交BD于点F,若EC=2BE,则=?
.?
10.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE=?
.?
11.
如图,在△ABC中,∠B=25°,AD是BC边上的高,且AD2=BD·DC,则∠BCA的度数为
.?
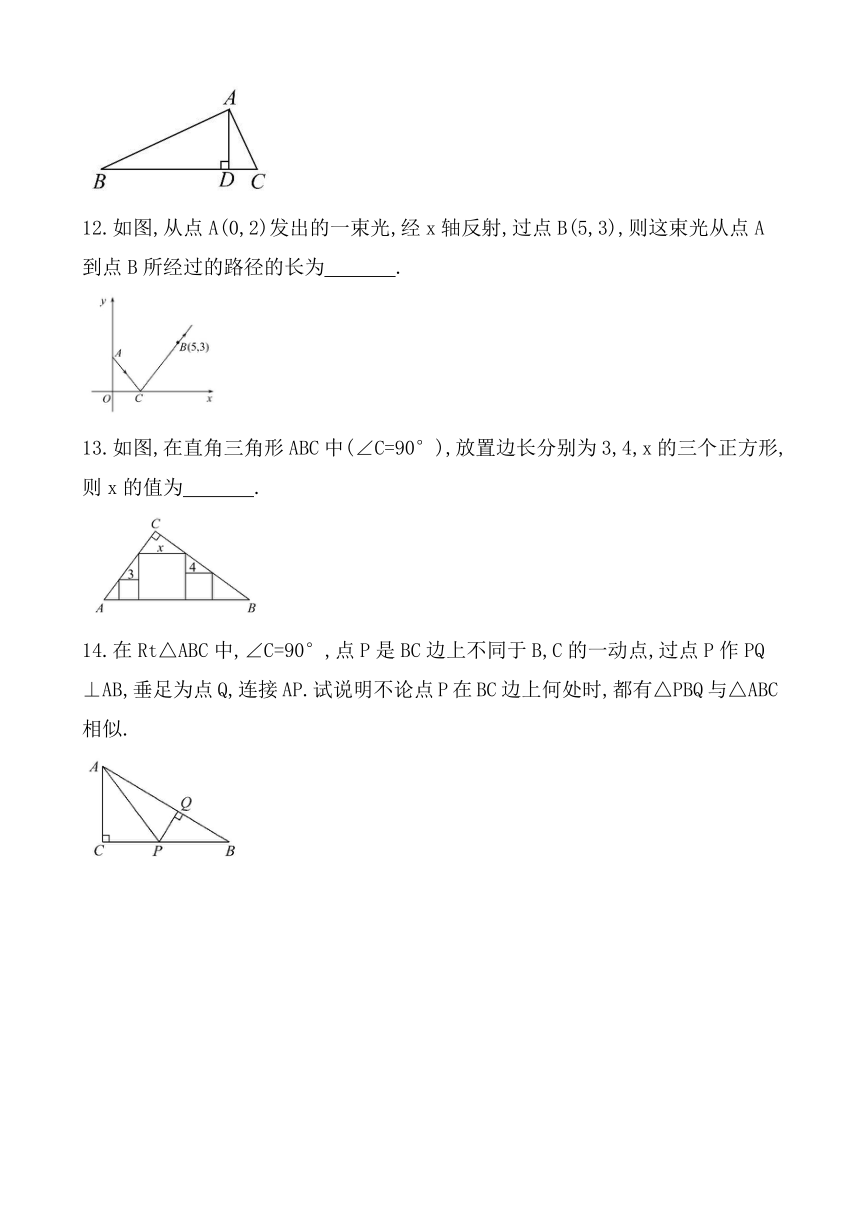
12.如图,从点A(0,2)发出的一束光,经x轴反射,过点B(5,3),则这束光从点A到点B所经过的路径的长为
.?
13.如图,在直角三角形ABC中(∠C=90°),放置边长分别为3,4,x的三个正方形,则x的值为
.
14.在Rt△ABC中,∠C=90°,点P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为点Q,连接AP.试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似.
15.如图所示,已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系式时,△ABC与△CDB相似?
16.如图,EC∥AB,∠EDA=∠ABF.
(1)求证:=,=.
(2)若OF=2,AE=3,求AF的长度.
北师大版九年级上册数学《相似三角形判定定理的证明》当堂达标试题
(解析版)
知识点回顾:
相似三角形判定定理的证明
相似三角形判定定理的证明的依据:
① 相似三角形 的定义;
②平行线分线段成比例定理.?
2.相似三角形判定定理的证明的思路:添加 平行 线,证明三角形相似.?
达标检测:
1.如图,下列条件不能判定△ADB∽△ABC的是
( D )
A.∠ABD=∠ACB
B.∠ADB=∠ABC
C.AB2=AD·AC
D.=
2.
如图,在△ABC中,点D,E分别是AB,AC边上的点,DE∥BC,AD=2,AB=3,DE=4,则BC等于( B )
A.5
B.6
C.7
D.8
3.
如图,在?ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是
( D )
A.=
B.=
C.=
D.=
4.如图,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,则下列各式正确的是( C )
①AD2=BD·DC;②CD2=CF·CA;③DE2=AE·AB;④AE·AB=AF·AC.
A.①②
B.①③
C.②④
D.③④
5.如图,AB⊥BD,CD⊥BD,垂足分别为点B,D,AD和BC相交于点E,EF⊥BD,垂足为点F.则下列结论错误的是
( A )
A.=
B.=
C.=
D.=
6.如图,在△ABC中,点D在边AB上,且满足∠ACD=∠ABC,若AC=2,AD=1,则DB的长为
( C )
A.1
B.2
C.3
D.4
7.
如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E,F,G,H分别落在边AD,AB,BC,CD上,则每个小正方形的边长为
( D )
A.6
B.5
C.2
D.
8.如图,在菱形ABCD中,点E是BC的中点,DE与AC交于点F,若AB=6,∠B=60°,则AF的长为
( D )
A.3
B.3.5
C.3
D.4
9.如图,在菱形ABCD中,E是BC边上的点,连接AE交BD于点F,若EC=2BE,则=? .?
10.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,
∠ABC的平分线BD交AC于点E,DE=? .?
11.
如图,在△ABC中,∠B=25°,AD是BC边上的高,且AD2=BD·DC,则∠BCA的度数为 65° .?
12.如图,从点A(0,2)发出的一束光,经x轴反射,过点B(5,3),则这束光从点A到点B所经过的路径的长为 5 .?
13.如图,在直角三角形ABC中(∠C=90°),放置边长分别为3,4,x的三个正方形,则x的值为 7 .
14.在Rt△ABC中,∠C=90°,点P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为点Q,连接AP.试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似.
【解析】不论点P在BC边上何处时,都有∠PQB=∠C=90°,∠B=∠B,
∴△PBQ∽△ABC.
15.如图所示,已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系式时,△ABC与△CDB相似?
【解析】①当BD与BC是对应边时,要使△ABC∽△CDB,则=,
∴=,∴BD=,即当BD=时,△ABC∽△CDB.
②当BD与AB为对应边时,在Rt△ABC中,AB==,
要使△ABC∽△BDC,则=,∴=.
∴BD=,即当BD=时,△ABC∽△BDC.
16.如图,EC∥AB,∠EDA=∠ABF.
(1)求证:=,=.
(2)若OF=2,AE=3,求AF的长度.
【解析】(1)∵EC∥AB,∴△OAB∽△OED,∴=.
∵△OAB∽△OED,∴∠OBA=∠ODE.∵∠EDA=∠ABF,∴∠OBF=∠ODA.
∵∠BOF=∠DOA,∴△OBF∽△ODA,∴=.
(2)∵=,=,∴=,即=,
∴AF=-1或AF=--1(不合题意,舍去),经检验,AF=-1是分式方程的解,
∴AF=-1.
-
4
-
知识点回顾:
相似三角形判定定理的证明
相似三角形判定定理的证明的依据:
①
的定义;
②平行线分线段成比例定理.?
2.相似三角形判定定理的证明的思路:添加
线,证明三角形相似.?
达标检测:
1.如图,下列条件不能判定△ADB∽△ABC的是
(
)
A.∠ABD=∠ACB
B.∠ADB=∠ABC
C.AB2=AD·AC
D.=
2.
如图,在△ABC中,点D,E分别是AB,AC边上的点,DE∥BC,AD=2,AB=3,DE=4,则BC等于(
)
A.5
B.6
C.7
D.8
3.
如图,在?ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是
(
)
A.=
B.=
C.=
D.=
4.如图,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,则下列各式正确的是(
)
①AD2=BD·DC;②CD2=CF·CA;③DE2=AE·AB;④AE·AB=AF·AC.
A.①②
B.①③
C.②④
D.③④
5.如图,AB⊥BD,CD⊥BD,垂足分别为点B,D,AD和BC相交于点E,EF⊥BD,垂足为点F.则下列结论错误的是
(
)
A.=
B.=
C.=
D.=
6.如图,在△ABC中,点D在边AB上,且满足∠ACD=∠ABC,若AC=2,AD=1,则DB的长为
(
)
A.1
B.2
C.3
D.4
7.
如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E,F,G,H分别落在边AD,AB,BC,CD上,则每个小正方形的边长为
(
)
A.6
B.5
C.2
D.
8.如图,在菱形ABCD中,点E是BC的中点,DE与AC交于点F,若AB=6,∠B=60°,则AF的长为
(
)
A.3
B.3.5
C.3
D.4
9.如图,在菱形ABCD中,E是BC边上的点,连接AE交BD于点F,若EC=2BE,则=?
.?
10.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,∠ABC的平分线BD交AC于点E,DE=?
.?
11.
如图,在△ABC中,∠B=25°,AD是BC边上的高,且AD2=BD·DC,则∠BCA的度数为
.?
12.如图,从点A(0,2)发出的一束光,经x轴反射,过点B(5,3),则这束光从点A到点B所经过的路径的长为
.?
13.如图,在直角三角形ABC中(∠C=90°),放置边长分别为3,4,x的三个正方形,则x的值为
.
14.在Rt△ABC中,∠C=90°,点P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为点Q,连接AP.试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似.
15.如图所示,已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系式时,△ABC与△CDB相似?
16.如图,EC∥AB,∠EDA=∠ABF.
(1)求证:=,=.
(2)若OF=2,AE=3,求AF的长度.
北师大版九年级上册数学《相似三角形判定定理的证明》当堂达标试题
(解析版)
知识点回顾:
相似三角形判定定理的证明
相似三角形判定定理的证明的依据:
① 相似三角形 的定义;
②平行线分线段成比例定理.?
2.相似三角形判定定理的证明的思路:添加 平行 线,证明三角形相似.?
达标检测:
1.如图,下列条件不能判定△ADB∽△ABC的是
( D )
A.∠ABD=∠ACB
B.∠ADB=∠ABC
C.AB2=AD·AC
D.=
2.
如图,在△ABC中,点D,E分别是AB,AC边上的点,DE∥BC,AD=2,AB=3,DE=4,则BC等于( B )
A.5
B.6
C.7
D.8
3.
如图,在?ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是
( D )
A.=
B.=
C.=
D.=
4.如图,AD⊥BC于点D,DE⊥AB于点E,DF⊥AC于点F,则下列各式正确的是( C )
①AD2=BD·DC;②CD2=CF·CA;③DE2=AE·AB;④AE·AB=AF·AC.
A.①②
B.①③
C.②④
D.③④
5.如图,AB⊥BD,CD⊥BD,垂足分别为点B,D,AD和BC相交于点E,EF⊥BD,垂足为点F.则下列结论错误的是
( A )
A.=
B.=
C.=
D.=
6.如图,在△ABC中,点D在边AB上,且满足∠ACD=∠ABC,若AC=2,AD=1,则DB的长为
( C )
A.1
B.2
C.3
D.4
7.
如图,正方形ABCD的边长为25,内部有6个全等的正方形,小正方形的顶点E,F,G,H分别落在边AD,AB,BC,CD上,则每个小正方形的边长为
( D )
A.6
B.5
C.2
D.
8.如图,在菱形ABCD中,点E是BC的中点,DE与AC交于点F,若AB=6,∠B=60°,则AF的长为
( D )
A.3
B.3.5
C.3
D.4
9.如图,在菱形ABCD中,E是BC边上的点,连接AE交BD于点F,若EC=2BE,则=? .?
10.如图,在Rt△ABC中,∠ACB=90°,AB=10,BC=6,CD∥AB,
∠ABC的平分线BD交AC于点E,DE=? .?
11.
如图,在△ABC中,∠B=25°,AD是BC边上的高,且AD2=BD·DC,则∠BCA的度数为 65° .?
12.如图,从点A(0,2)发出的一束光,经x轴反射,过点B(5,3),则这束光从点A到点B所经过的路径的长为 5 .?
13.如图,在直角三角形ABC中(∠C=90°),放置边长分别为3,4,x的三个正方形,则x的值为 7 .
14.在Rt△ABC中,∠C=90°,点P是BC边上不同于B,C的一动点,过点P作PQ⊥AB,垂足为点Q,连接AP.试说明不论点P在BC边上何处时,都有△PBQ与△ABC相似.
【解析】不论点P在BC边上何处时,都有∠PQB=∠C=90°,∠B=∠B,
∴△PBQ∽△ABC.
15.如图所示,已知∠ABC=∠CDB=90°,AC=a,BC=b,当BD与a,b之间满足怎样的关系式时,△ABC与△CDB相似?
【解析】①当BD与BC是对应边时,要使△ABC∽△CDB,则=,
∴=,∴BD=,即当BD=时,△ABC∽△CDB.
②当BD与AB为对应边时,在Rt△ABC中,AB==,
要使△ABC∽△BDC,则=,∴=.
∴BD=,即当BD=时,△ABC∽△BDC.
16.如图,EC∥AB,∠EDA=∠ABF.
(1)求证:=,=.
(2)若OF=2,AE=3,求AF的长度.
【解析】(1)∵EC∥AB,∴△OAB∽△OED,∴=.
∵△OAB∽△OED,∴∠OBA=∠ODE.∵∠EDA=∠ABF,∴∠OBF=∠ODA.
∵∠BOF=∠DOA,∴△OBF∽△ODA,∴=.
(2)∵=,=,∴=,即=,
∴AF=-1或AF=--1(不合题意,舍去),经检验,AF=-1是分式方程的解,
∴AF=-1.
-
4
-
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
