北师大版八年级上册数学 4.4 一次函数的应用 同步练习(Word版 含解析)
文档属性
| 名称 | 北师大版八年级上册数学 4.4 一次函数的应用 同步练习(Word版 含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 156.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-21 00:00:00 | ||
图片预览


文档简介
4.4
一次函数的应用
同步练习
一.选择题
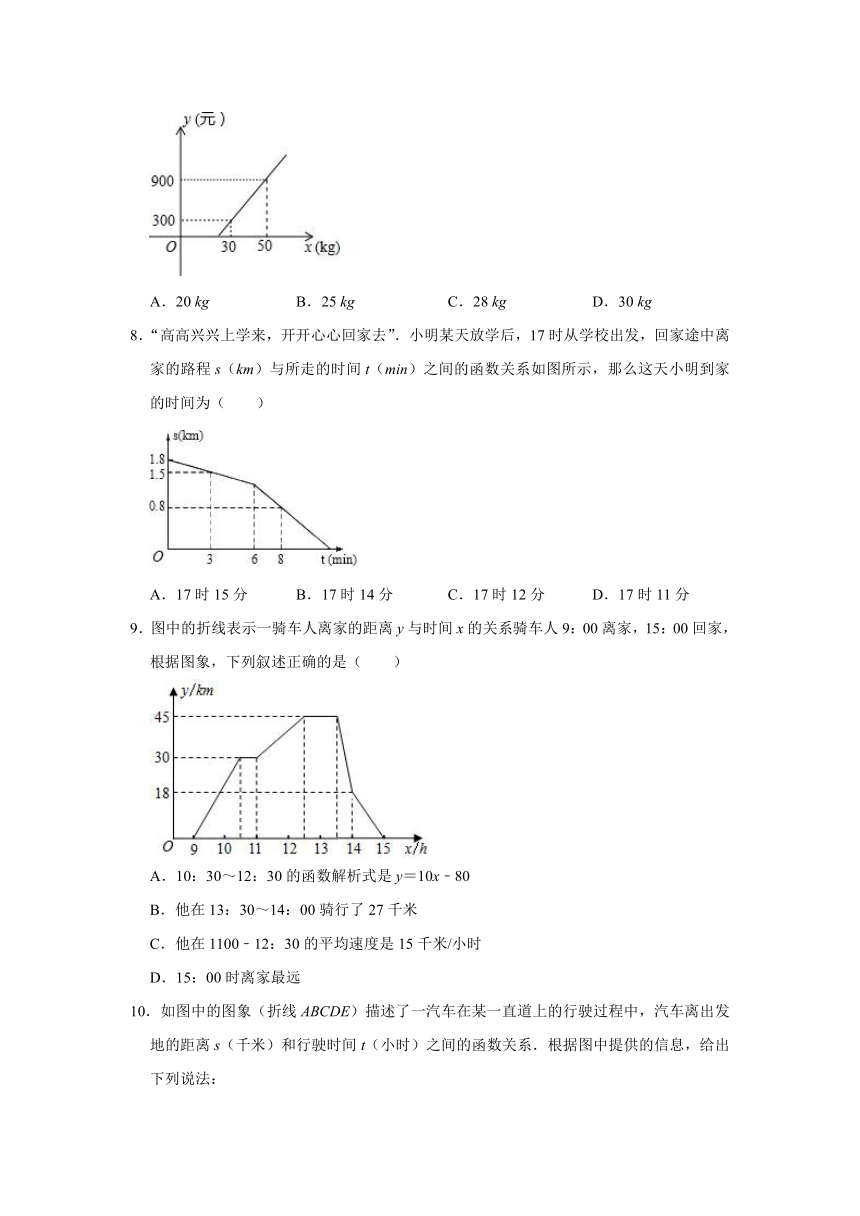
1.一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图象可以表示为图中的( )
A.
B.
C.
D.
2.如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是( )
A.(4,2)
B.(2,4)
C.(,3)
D.(2+2,2)
3.甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等
D.从出发到13.7秒的时间段内,乙队的速度慢
4.甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( )
A.甲车的平均速度为60km/h
B.乙车的平均速度为100km/h
C.乙车比甲车先到B城
D.乙车比甲车先出发1h
5.某复印的收费y(元)与复印页数x(页)的关系如下表:
x(页)
100
200
400
1000
……
y(元)
40
80
160
400
……
若某客户复印1200页,则该客户应付复印费( )
A.3000元
B.1200元
C.560元
D.480元
6.如图,弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数,则弹簧不挂物体时的长度为( )cm.
A.9
B.10
C.11
D.12
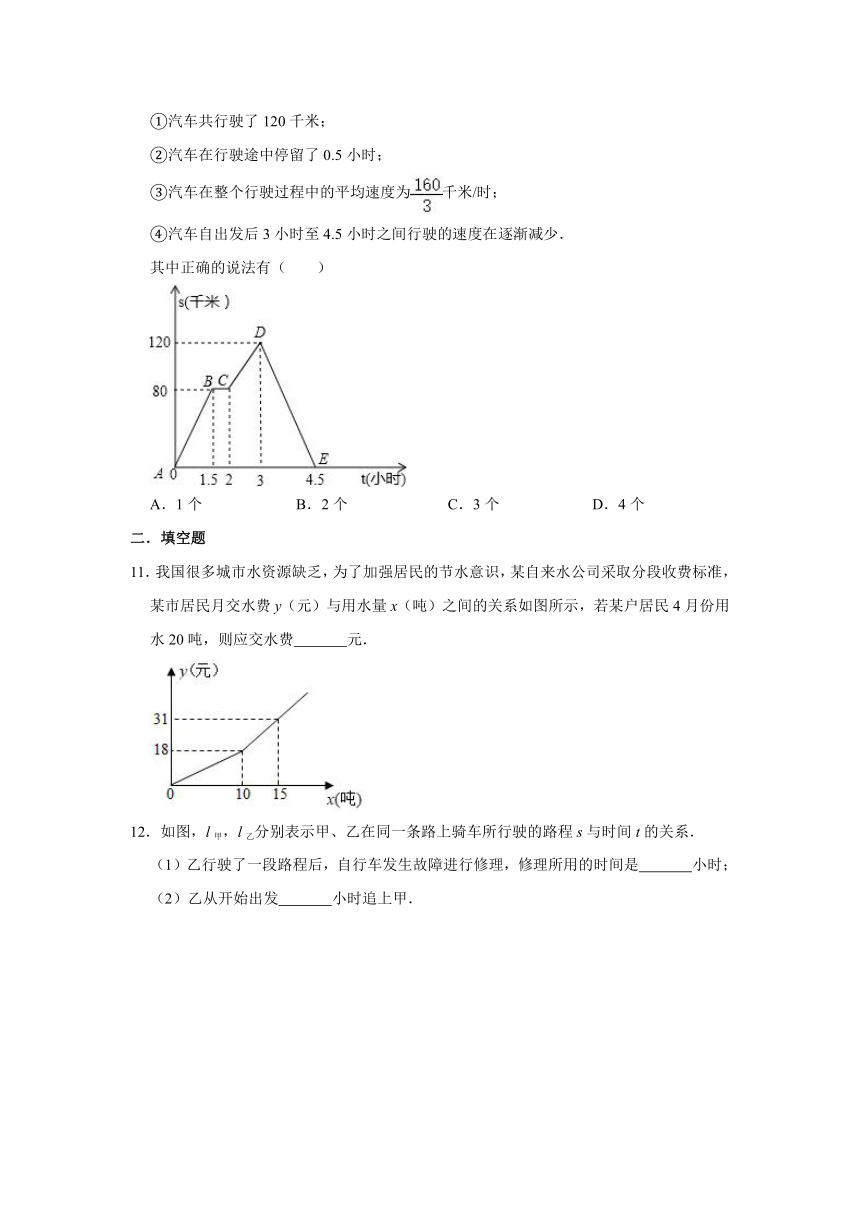
7.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20
kg
B.25
kg
C.28
kg
D.30
kg
8.“高高兴兴上学来,开开心心回家去”.小明某天放学后,17时从学校出发,回家途中离家的路程s(km)与所走的时间t(min)之间的函数关系如图所示,那么这天小明到家的时间为( )
A.17时15分
B.17时14分
C.17时12分
D.17时11分
9.图中的折线表示一骑车人离家的距离y与时间x的关系骑车人9:00离家,15:00回家,根据图象,下列叙述正确的是( )
A.10:30~12:30的函数解析式是y=10x﹣80
B.他在13:30~14:00骑行了27千米
C.他在1100﹣12:30的平均速度是15千米/小时
D.15:00时离家最远
10.如图中的图象(折线ABCDE)描述了一汽车在某一直道上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法有( )
A.1个
B.2个
C.3个
D.4个
二.填空题
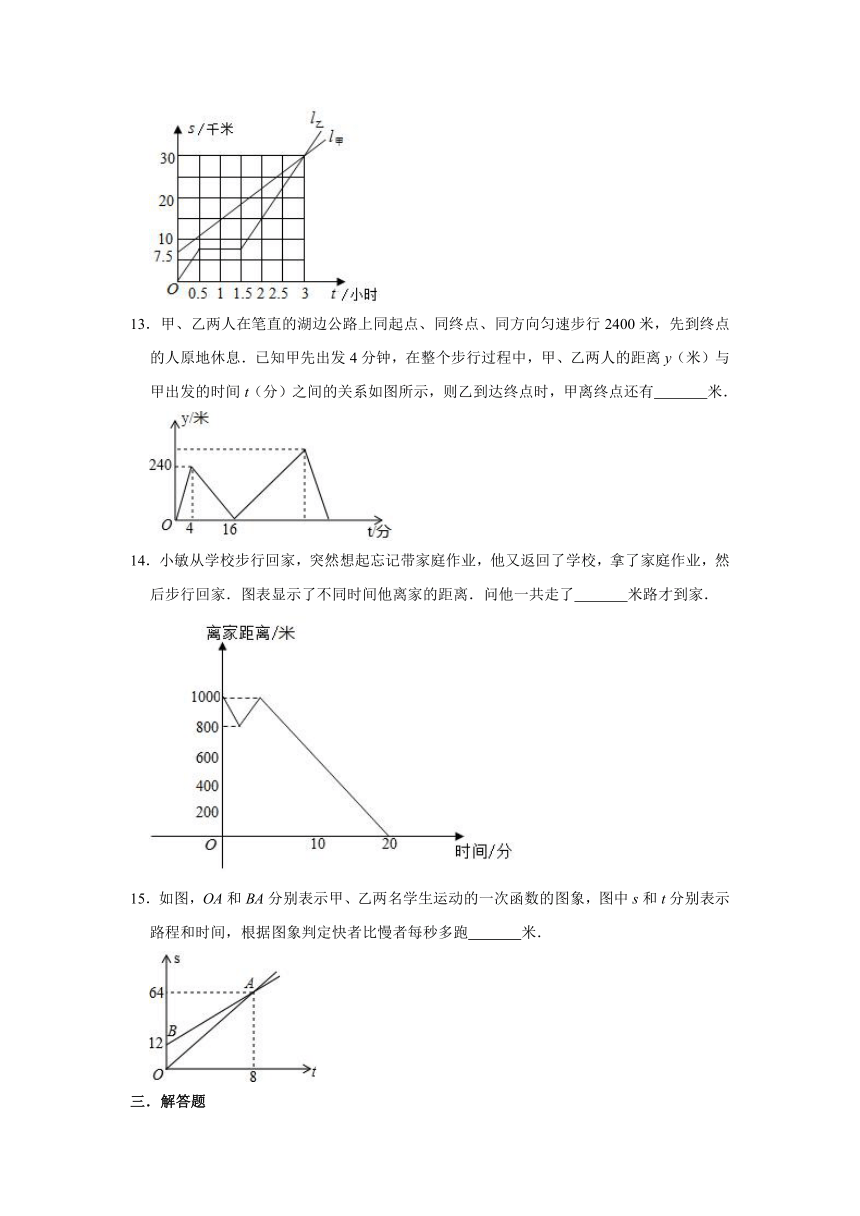
11.我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水20吨,则应交水费
元.
12.如图,l甲,l乙分别表示甲、乙在同一条路上骑车所行驶的路程s与时间t的关系.
(1)乙行驶了一段路程后,自行车发生故障进行修理,修理所用的时间是
小时;
(2)乙从开始出发
小时追上甲.
13.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则乙到达终点时,甲离终点还有
米.
14.小敏从学校步行回家,突然想起忘记带家庭作业,他又返回了学校,拿了家庭作业,然后步行回家.图表显示了不同时间他离家的距离.问他一共走了
米路才到家.
15.如图,OA和BA分别表示甲、乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定快者比慢者每秒多跑
米.
三.解答题
16.某种动物的身高y(dm)是其腿长x(dm)的一次函数.当动物的腿长为6dm时,身高为45.5dm;当动物的腿长为14dm时,身高为105.5dm.
(1)写出y与x之间的关系式;
(2)当该动物腿长10dm时,其身高为多少?
17.某天,一蔬菜经营户从蔬菜批发市场批发了黄瓜和茄子共60千克,到菜市场去卖,黄瓜和茄子当天的批发价和零售价如表表示:
品名
黄瓜
茄子
批发价/(元/千克)
2.4
2.2
零售价/(元/千克)
3.6
3
(1)若他当天批发两种蔬菜共花去140元,则卖完这些黄瓜和茄子可赚多少元?
(2)设全部售出60千克蔬菜的总利润为y(元),黄瓜的批发量a(千克),请写出y与a的函数关系式,并求最大利润为多少?
18.甲、乙两人开车匀速从同一地点到距离出发地480千米处的景点旅游,甲出发半小时后,乙以每小时80千米的速度沿同一路线行驶,两车分别到达目的地后停止.甲、乙两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示.
(1)甲行驶的速度是
千米/小时.
(2)求乙车追上甲车后,y与x之间的函数关系式,并写出自变量x的取值范围.
(3)求甲车出发多长时间两车相距75千米.
参考答案
1.解:由题意,得
y=30﹣5t,
∵y≥0,t≥0,
∴30﹣5t≥0,
∴t≤6,
∴0≤t≤6,
∴y=30﹣5t是降函数且图象是一条线段.
故选:B.
2.解:在y=﹣x+2中令x=0,解得:y=2;
令y=0,解得:x=2.
则OA=2,OB=2.
∴在直角△ABO中,AB==4,∠BAO=30°,
又∵∠BAB′=60°,
∴∠OAB′=90°,
∴B′的坐标是(2,4).
故选:B.
3.解:A、由函数图象可知,甲走完全程需要82.3秒,乙走完全程需要90.2秒,甲队率先到达终点,本选项错误;
B、由函数图象可知,甲、乙两队都走了300米,路程相同,本选项错误;
C、由函数图象可知,在47.8秒时,两队所走路程相等,均为174米,本选项正确;
D、由函数图象可知,从出发到13.7秒的时间段内,甲队的速度慢,本选项错误;
故选:C.
4.解:由图象知:
A.甲车的平均速度为=60km/h,故A选项不合题意;
B.乙车的平均速度为=100km/h,故B选项不合题意;
C.甲10时到达B城,乙9时到达B城,所以乙比甲先到B城,故C选项不合题意;
D.甲5时出发,乙6时出发,所以乙比甲晚出发1h,故此选项错误,
故选:D.
5.解:由表中数据变化关系可知:在y随x变化而变化的过程中,变量y与x的商一定,则y是x的正比例函数,
不妨设y=kx(k≠0),
把x=100,y=40代入得,40=100k,
解得,k=0.4,
∴y=0.4x,
当x=1200时,y=0.4×1200=480,
故选:D.
6.解:设直线的函数表达式为y=kx+b,
∵x=6时,y=15;x=20时,y=22;
∴
∴①﹣②得:14k=7,
∴k=,
把k=代入到①得:b=12,
当x=0时,y=.
故选:D.
7.解:设y与x的函数关系式为y=kx+b,
由题意可知,
解得,
所以函数关系式为y=30x﹣600,
当y=0时,即30x﹣600=0,所以x=20.
故选:A.
8.解:前段的速度为(1.8﹣1.5)÷3=0.1,所以6分钟走了0.6km.
后段有1.8﹣0.6=1.2km,速度为(1.2﹣0.8)÷(8﹣6)=0.2,所需时间1.2÷0.2=6.
所以途中共用时6+6=12分钟,到家时间是17时12分.
故选:C.
9.解:从图象可知:10:30~12:30的函数是分段函数,因此不正确;他在13:30~14:00之间路程由45千米减小到18千米,因此骑行了27千米是正确的;他在
11:00﹣12:30的平均速度是10千米/小时不是15千米/小时,因此是不正确的;15:00时回到家,不是离家最远,
故选:B.
10.解:①由图可知,汽车共行驶了120×2=240千米,故本小题错误;
②汽车在行驶途中停留了2﹣1.5=0.5小时,故本小题正确;
③汽车在整个行驶过程中的平均速度为=千米/时,故本小题正确;
④汽车自出发后3小时至4.5小时之间行驶离出发地越来越近,是匀速运动,故本小题错误;
综上所述,正确的说法有②③共2个.
故选:B.
11.解:由图象可知,
超出10吨的部分,每吨水的价格是(31﹣18)÷(15﹣10)=2.6(元),
当用水20吨时,应交水费:18+(20﹣10)×2.6=44(元),
故答案为:44.
12.解:(1)1.5﹣0.5=1(小时),
即修理所用的时间是1小时;
(2)由题意可知,乙从开始出发3小时追上甲.
故答案为:(1)1;(2)3.
13.解:设甲的速度为v1米/分钟,乙的速度为v2米/分钟,
∴v1==60米/分钟,
由图象可知:乙追上甲需要12分钟,
∴12v2=240+12×60,
∴v2=80米/分钟,
∴此时乙共走了12×80=960米,
∴乙离终点还有2400﹣960=1440米,
∴乙到达终点时需要的时间为:=18分钟,
∴甲离终点还有1440﹣18×60=360米,
故答案为:360.
14.解:小敏一共走了:(1000﹣800)×2+1000=1400(米).
故答案为:1400.
15.解:如图所示:快者的速度为:64÷8=8(m/s),
慢者的速度为:(64﹣12)÷8=6.5(m/s),
8﹣6.5=1.5(米),
所以快者比慢者每秒多跑1.5米.
故答案为:1.5
16.解:(1)设y与x之间的关系式为y=kx+b,
,得,
即y与x之间的关系式是y=7.5x+0.5;
(2)当x=10时,y=7.5×10+0.5=75.5,
答:当该动物腿长10dm时,其身高为75.5dm.
17.解:(1)设一蔬菜经营户从蔬菜批发市场批发了黄瓜xkg,
2.4x+2.2(60﹣x)=140
解得,x=40
60﹣x=20,
则卖完这些黄瓜和茄子可赚:(3.6﹣2.4)×40+(3﹣2.2)×20=64(元),
即卖完这些黄瓜和茄子可赚64元;
(2)由题意可得,
y=(3.6﹣2.4)×a+(3﹣2.2)×(60﹣a)=0.4a+48
∵0≤a≤60,
∴当a=60时,y=0.4a+48取得最大值,此时y=72,
即y与a的函数关系式是y=0.4a+48,最大利润为72元.
18.解:(1)甲行驶的速度为:30÷0.5=60(千米/小时),
故答案为:60.
(2)如图所示:
设甲出发x小时后被乙追上,根据题意得:
60x=80(x﹣0.5),
解得x=2,
即甲出发2小时后被乙追上,
∴点A的坐标为(2,0),
480÷80+0.5=6.5(时),
即点B的坐标为(6.5,90),
设AB的解析式为y=kx+b,由点A,B的坐标可得:
,解得,
所以AB的解析式为y=20x﹣40(2≤x≤6.5);
(3)根据题意得20x﹣40=75或60x=480﹣75,
解得x=或
答:甲车出发小时或小时两车相距75千米.
一次函数的应用
同步练习
一.选择题
1.一根蜡烛长30cm,点燃后每小时燃烧5cm,燃烧时蜡烛剩余的长度h(cm)和燃烧时间t(小时)之间的函数关系用图象可以表示为图中的( )
A.
B.
C.
D.
2.如图,直线y=﹣x+2与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△AO′B′,则点B′的坐标是( )
A.(4,2)
B.(2,4)
C.(,3)
D.(2+2,2)
3.甲、乙两队参加了“端午情,龙舟韵”赛龙舟比赛,两队在比赛时的路程s(米)与时间t(秒)之间的函数图象如图所示,请你根据图象判断,下列说法正确的是( )
A.乙队率先到达终点
B.甲队比乙队多走了126米
C.在47.8秒时,两队所走路程相等
D.从出发到13.7秒的时间段内,乙队的速度慢
4.甲乙两车从A城出发前往B城,在整个行程中,汽车离开A城的距离y与时刻t的对应关系如图所示,则下列结论错误的是( )
A.甲车的平均速度为60km/h
B.乙车的平均速度为100km/h
C.乙车比甲车先到B城
D.乙车比甲车先出发1h
5.某复印的收费y(元)与复印页数x(页)的关系如下表:
x(页)
100
200
400
1000
……
y(元)
40
80
160
400
……
若某客户复印1200页,则该客户应付复印费( )
A.3000元
B.1200元
C.560元
D.480元
6.如图,弹簧的长度y(cm)与所挂物体的质量x(kg)之间的关系是一次函数,则弹簧不挂物体时的长度为( )cm.
A.9
B.10
C.11
D.12
7.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,那么旅客可携带的免费行李的最大质量为( )
A.20
kg
B.25
kg
C.28
kg
D.30
kg
8.“高高兴兴上学来,开开心心回家去”.小明某天放学后,17时从学校出发,回家途中离家的路程s(km)与所走的时间t(min)之间的函数关系如图所示,那么这天小明到家的时间为( )
A.17时15分
B.17时14分
C.17时12分
D.17时11分
9.图中的折线表示一骑车人离家的距离y与时间x的关系骑车人9:00离家,15:00回家,根据图象,下列叙述正确的是( )
A.10:30~12:30的函数解析式是y=10x﹣80
B.他在13:30~14:00骑行了27千米
C.他在1100﹣12:30的平均速度是15千米/小时
D.15:00时离家最远
10.如图中的图象(折线ABCDE)描述了一汽车在某一直道上的行驶过程中,汽车离出发地的距离s(千米)和行驶时间t(小时)之间的函数关系.根据图中提供的信息,给出下列说法:
①汽车共行驶了120千米;
②汽车在行驶途中停留了0.5小时;
③汽车在整个行驶过程中的平均速度为千米/时;
④汽车自出发后3小时至4.5小时之间行驶的速度在逐渐减少.
其中正确的说法有( )
A.1个
B.2个
C.3个
D.4个
二.填空题
11.我国很多城市水资源缺乏,为了加强居民的节水意识,某自来水公司采取分段收费标准,某市居民月交水费y(元)与用水量x(吨)之间的关系如图所示,若某户居民4月份用水20吨,则应交水费
元.
12.如图,l甲,l乙分别表示甲、乙在同一条路上骑车所行驶的路程s与时间t的关系.
(1)乙行驶了一段路程后,自行车发生故障进行修理,修理所用的时间是
小时;
(2)乙从开始出发
小时追上甲.
13.甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,则乙到达终点时,甲离终点还有
米.
14.小敏从学校步行回家,突然想起忘记带家庭作业,他又返回了学校,拿了家庭作业,然后步行回家.图表显示了不同时间他离家的距离.问他一共走了
米路才到家.
15.如图,OA和BA分别表示甲、乙两名学生运动的一次函数的图象,图中s和t分别表示路程和时间,根据图象判定快者比慢者每秒多跑
米.
三.解答题
16.某种动物的身高y(dm)是其腿长x(dm)的一次函数.当动物的腿长为6dm时,身高为45.5dm;当动物的腿长为14dm时,身高为105.5dm.
(1)写出y与x之间的关系式;
(2)当该动物腿长10dm时,其身高为多少?
17.某天,一蔬菜经营户从蔬菜批发市场批发了黄瓜和茄子共60千克,到菜市场去卖,黄瓜和茄子当天的批发价和零售价如表表示:
品名
黄瓜
茄子
批发价/(元/千克)
2.4
2.2
零售价/(元/千克)
3.6
3
(1)若他当天批发两种蔬菜共花去140元,则卖完这些黄瓜和茄子可赚多少元?
(2)设全部售出60千克蔬菜的总利润为y(元),黄瓜的批发量a(千克),请写出y与a的函数关系式,并求最大利润为多少?
18.甲、乙两人开车匀速从同一地点到距离出发地480千米处的景点旅游,甲出发半小时后,乙以每小时80千米的速度沿同一路线行驶,两车分别到达目的地后停止.甲、乙两车之间的距离y(千米)与甲车行驶的时间x(小时)之间的函数关系如图所示.
(1)甲行驶的速度是
千米/小时.
(2)求乙车追上甲车后,y与x之间的函数关系式,并写出自变量x的取值范围.
(3)求甲车出发多长时间两车相距75千米.
参考答案
1.解:由题意,得
y=30﹣5t,
∵y≥0,t≥0,
∴30﹣5t≥0,
∴t≤6,
∴0≤t≤6,
∴y=30﹣5t是降函数且图象是一条线段.
故选:B.
2.解:在y=﹣x+2中令x=0,解得:y=2;
令y=0,解得:x=2.
则OA=2,OB=2.
∴在直角△ABO中,AB==4,∠BAO=30°,
又∵∠BAB′=60°,
∴∠OAB′=90°,
∴B′的坐标是(2,4).
故选:B.
3.解:A、由函数图象可知,甲走完全程需要82.3秒,乙走完全程需要90.2秒,甲队率先到达终点,本选项错误;
B、由函数图象可知,甲、乙两队都走了300米,路程相同,本选项错误;
C、由函数图象可知,在47.8秒时,两队所走路程相等,均为174米,本选项正确;
D、由函数图象可知,从出发到13.7秒的时间段内,甲队的速度慢,本选项错误;
故选:C.
4.解:由图象知:
A.甲车的平均速度为=60km/h,故A选项不合题意;
B.乙车的平均速度为=100km/h,故B选项不合题意;
C.甲10时到达B城,乙9时到达B城,所以乙比甲先到B城,故C选项不合题意;
D.甲5时出发,乙6时出发,所以乙比甲晚出发1h,故此选项错误,
故选:D.
5.解:由表中数据变化关系可知:在y随x变化而变化的过程中,变量y与x的商一定,则y是x的正比例函数,
不妨设y=kx(k≠0),
把x=100,y=40代入得,40=100k,
解得,k=0.4,
∴y=0.4x,
当x=1200时,y=0.4×1200=480,
故选:D.
6.解:设直线的函数表达式为y=kx+b,
∵x=6时,y=15;x=20时,y=22;
∴
∴①﹣②得:14k=7,
∴k=,
把k=代入到①得:b=12,
当x=0时,y=.
故选:D.
7.解:设y与x的函数关系式为y=kx+b,
由题意可知,
解得,
所以函数关系式为y=30x﹣600,
当y=0时,即30x﹣600=0,所以x=20.
故选:A.
8.解:前段的速度为(1.8﹣1.5)÷3=0.1,所以6分钟走了0.6km.
后段有1.8﹣0.6=1.2km,速度为(1.2﹣0.8)÷(8﹣6)=0.2,所需时间1.2÷0.2=6.
所以途中共用时6+6=12分钟,到家时间是17时12分.
故选:C.
9.解:从图象可知:10:30~12:30的函数是分段函数,因此不正确;他在13:30~14:00之间路程由45千米减小到18千米,因此骑行了27千米是正确的;他在
11:00﹣12:30的平均速度是10千米/小时不是15千米/小时,因此是不正确的;15:00时回到家,不是离家最远,
故选:B.
10.解:①由图可知,汽车共行驶了120×2=240千米,故本小题错误;
②汽车在行驶途中停留了2﹣1.5=0.5小时,故本小题正确;
③汽车在整个行驶过程中的平均速度为=千米/时,故本小题正确;
④汽车自出发后3小时至4.5小时之间行驶离出发地越来越近,是匀速运动,故本小题错误;
综上所述,正确的说法有②③共2个.
故选:B.
11.解:由图象可知,
超出10吨的部分,每吨水的价格是(31﹣18)÷(15﹣10)=2.6(元),
当用水20吨时,应交水费:18+(20﹣10)×2.6=44(元),
故答案为:44.
12.解:(1)1.5﹣0.5=1(小时),
即修理所用的时间是1小时;
(2)由题意可知,乙从开始出发3小时追上甲.
故答案为:(1)1;(2)3.
13.解:设甲的速度为v1米/分钟,乙的速度为v2米/分钟,
∴v1==60米/分钟,
由图象可知:乙追上甲需要12分钟,
∴12v2=240+12×60,
∴v2=80米/分钟,
∴此时乙共走了12×80=960米,
∴乙离终点还有2400﹣960=1440米,
∴乙到达终点时需要的时间为:=18分钟,
∴甲离终点还有1440﹣18×60=360米,
故答案为:360.
14.解:小敏一共走了:(1000﹣800)×2+1000=1400(米).
故答案为:1400.
15.解:如图所示:快者的速度为:64÷8=8(m/s),
慢者的速度为:(64﹣12)÷8=6.5(m/s),
8﹣6.5=1.5(米),
所以快者比慢者每秒多跑1.5米.
故答案为:1.5
16.解:(1)设y与x之间的关系式为y=kx+b,
,得,
即y与x之间的关系式是y=7.5x+0.5;
(2)当x=10时,y=7.5×10+0.5=75.5,
答:当该动物腿长10dm时,其身高为75.5dm.
17.解:(1)设一蔬菜经营户从蔬菜批发市场批发了黄瓜xkg,
2.4x+2.2(60﹣x)=140
解得,x=40
60﹣x=20,
则卖完这些黄瓜和茄子可赚:(3.6﹣2.4)×40+(3﹣2.2)×20=64(元),
即卖完这些黄瓜和茄子可赚64元;
(2)由题意可得,
y=(3.6﹣2.4)×a+(3﹣2.2)×(60﹣a)=0.4a+48
∵0≤a≤60,
∴当a=60时,y=0.4a+48取得最大值,此时y=72,
即y与a的函数关系式是y=0.4a+48,最大利润为72元.
18.解:(1)甲行驶的速度为:30÷0.5=60(千米/小时),
故答案为:60.
(2)如图所示:
设甲出发x小时后被乙追上,根据题意得:
60x=80(x﹣0.5),
解得x=2,
即甲出发2小时后被乙追上,
∴点A的坐标为(2,0),
480÷80+0.5=6.5(时),
即点B的坐标为(6.5,90),
设AB的解析式为y=kx+b,由点A,B的坐标可得:
,解得,
所以AB的解析式为y=20x﹣40(2≤x≤6.5);
(3)根据题意得20x﹣40=75或60x=480﹣75,
解得x=或
答:甲车出发小时或小时两车相距75千米.
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
