人教版九年级上册数学 第二十四章 圆 24.2.2 直线和圆的位置关系 同步测试(Word版 含解析)
文档属性
| 名称 | 人教版九年级上册数学 第二十四章 圆 24.2.2 直线和圆的位置关系 同步测试(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 101.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 05:48:47 | ||
图片预览


文档简介
24.2.2
直线和圆的位置关系
同步测试
一.选择题
1.如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=20°,则∠AOB的度数为( )
A.40°
B.50°
C.60°
D.70°
2.如图,△ABC内接于圆,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62°
B.31°
C.28°
D.56°
3.已知⊙O的半径为7,直线l与⊙O相交,点O到直线l的距离为4,则⊙O上到直线l的距离为3的点共有( )
A.1个
B.2个
C.3个
D.4个
4.已知⊙O的半径为6cm,圆心O到直线a的距离为6cm,则直线a与⊙O的位置关系为( )
A.相交
B.相切
C.相离
D.无法确定
5.圆的直径是10cm,若圆心与直线的距离是5cm,则该直线和圆的位置关系是( )
A.相离
B.相切
C.相交
D.相交或相切
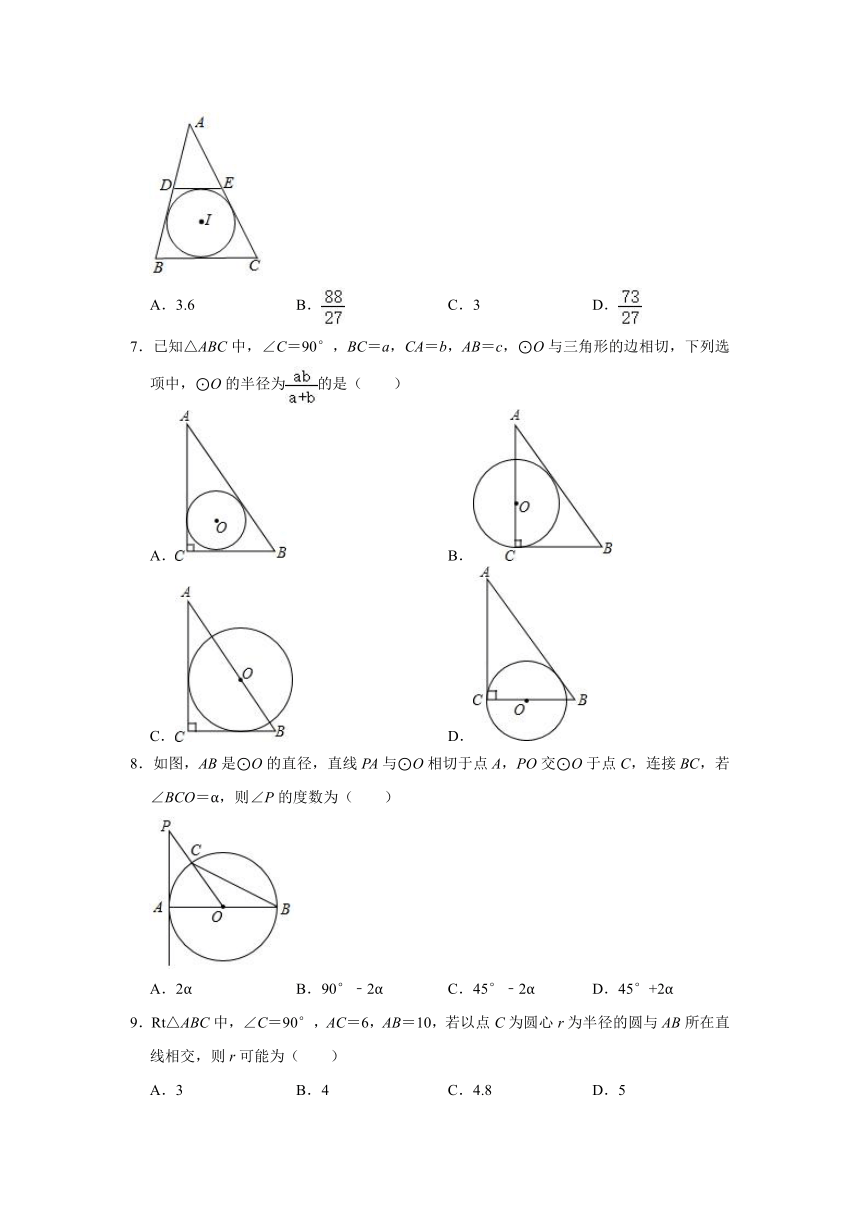
6.如图,⊙I为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE与⊙I相切,DE∥BC,则DE的长( )
A.3.6
B.
C.3
D.
7.已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为的是( )
A.
B.
C.
D.
8.如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC,若∠BCO=α,则∠P的度数为( )
A.2α
B.90°﹣2α
C.45°﹣2α
D.45°+2α
9.Rt△ABC中,∠C=90°,AC=6,AB=10,若以点C为圆心r为半径的圆与AB所在直线相交,则r可能为( )
A.3
B.4
C.4.8
D.5
10.如图,射线BM与⊙O相切于点B,若∠MBA=140°,则∠ACB的度数为( )
A.40°
B.50°
C.60°
D.70
二.填空题
11.已知△ABC的三边a、b、c满足b+|c﹣3|+a2﹣8a=4﹣19,则△ABC的内切圆半径=
.
12.如图,已知AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD.若∠C=40°,则∠B的度数是
°.
13.直线l经过点A
(4,0),B(0,2),若⊙M的半径为1,圆心M在x轴上,当⊙M与直线l相切时,则点M的坐标
.
14.如图,BC是⊙O的直径,AB、AD是⊙O的切线,若∠C=40°,则∠A的度数为
.
15.如图,BC是⊙O的切线,D是切点.连接BO并延长,交⊙O于点E、A,过A作AC⊥BC,垂足为C.若BD=8,BE=4,则AC=
.
三.解答题
16.如图,在Rt△ABC中,∠ACB=90°,BO平分∠ABC,交AC于点O,以O为圆心,OC为半径作圆,交OB于点E.
(1)求证:AB与⊙O相切;
(2)连接CE并延长,交AB于点F,若CF⊥AB,且CF=3,求⊙O的半径.
17.如图,△ABC外切于⊙O,切点分别为D、E、F,BC=7,⊙O的半径为,
(1)∠A=60°,求△ABC的周长.
(2)若∠A=70°,点M为⊙O上异于F、E的动点,则∠FME的度数为
°.
参考答案
1.D
2.B
3.C
4.B
5.B
6.B
7.C
8.B
9.D
10.A
11.1
12.25
13.M(4﹣,0)或(4+,0),
14.100°
15.9.6
16.(1)证明:作OD⊥AB于D,如图,
∵BO平分∠ABC,OC⊥BC,OD⊥AB,
∴OD=OC,
而OC为⊙O的半径,
∴AB与⊙O相切;
(2)作OH⊥CE于H,如图,设⊙O的半径为r,
易得四边形OHFD为矩形,
∴HF=OD=r,
∵OC=OE,OH⊥CE,
∴∠OCH=∠EOH,
∵OH∥BF,
∴∠CBO=∠BOH,
∵∠COH+∠BOH+∠CBO=90°,
∴∠COH=30°,
在Rt△OCH中,CH=CF﹣HF=3﹣r,
∵CH=OC,
∴3﹣r=r,解得r=2,
即⊙O的半径为2.
17.解:(1)连接OE、OF、OA,如图,
∵△ABC外切于⊙O,切点分别为D、E、F,
∴BD=BF,CD=CE,OE⊥AC,OF⊥AB,OA平分∠BAC,
∴∠OAE=×60°=30°,
∴AE=OE=×=3,
∴△ABC的周长=BC+BF+AF+AE+CE=BC+BD+CD+2AE=2BC+2AE=2×7+2×3=1=20;
(2)∵OE⊥AC,OF⊥AB,
∴∠OEA=∠OFA=90°,
∴∠EOF=180°﹣∠BAC=180°﹣70°=110°,
当点M在上时,如图,∠FME=∠EOF=55°;
当点M在上时,如图,∠FM′E=180°﹣55°=125°,
综上所述,∠FME的度数为55°或125°.
故答案为55或125.
直线和圆的位置关系
同步测试
一.选择题
1.如图,AB是⊙O的切线,A为切点,连接OA,OB,若∠B=20°,则∠AOB的度数为( )
A.40°
B.50°
C.60°
D.70°
2.如图,△ABC内接于圆,∠ACB=90°,过点C的切线交AB的延长线于点P,∠P=28°.则∠CAB=( )
A.62°
B.31°
C.28°
D.56°
3.已知⊙O的半径为7,直线l与⊙O相交,点O到直线l的距离为4,则⊙O上到直线l的距离为3的点共有( )
A.1个
B.2个
C.3个
D.4个
4.已知⊙O的半径为6cm,圆心O到直线a的距离为6cm,则直线a与⊙O的位置关系为( )
A.相交
B.相切
C.相离
D.无法确定
5.圆的直径是10cm,若圆心与直线的距离是5cm,则该直线和圆的位置关系是( )
A.相离
B.相切
C.相交
D.相交或相切
6.如图,⊙I为△ABC的内切圆,AB=9,BC=8,CA=10,点D,E分别为AB,AC上的点,且DE与⊙I相切,DE∥BC,则DE的长( )
A.3.6
B.
C.3
D.
7.已知△ABC中,∠C=90°,BC=a,CA=b,AB=c,⊙O与三角形的边相切,下列选项中,⊙O的半径为的是( )
A.
B.
C.
D.
8.如图,AB是⊙O的直径,直线PA与⊙O相切于点A,PO交⊙O于点C,连接BC,若∠BCO=α,则∠P的度数为( )
A.2α
B.90°﹣2α
C.45°﹣2α
D.45°+2α
9.Rt△ABC中,∠C=90°,AC=6,AB=10,若以点C为圆心r为半径的圆与AB所在直线相交,则r可能为( )
A.3
B.4
C.4.8
D.5
10.如图,射线BM与⊙O相切于点B,若∠MBA=140°,则∠ACB的度数为( )
A.40°
B.50°
C.60°
D.70
二.填空题
11.已知△ABC的三边a、b、c满足b+|c﹣3|+a2﹣8a=4﹣19,则△ABC的内切圆半径=
.
12.如图,已知AB是⊙O的直径,AC是⊙O的切线,连接OC交⊙O于点D,连接BD.若∠C=40°,则∠B的度数是
°.
13.直线l经过点A
(4,0),B(0,2),若⊙M的半径为1,圆心M在x轴上,当⊙M与直线l相切时,则点M的坐标
.
14.如图,BC是⊙O的直径,AB、AD是⊙O的切线,若∠C=40°,则∠A的度数为
.
15.如图,BC是⊙O的切线,D是切点.连接BO并延长,交⊙O于点E、A,过A作AC⊥BC,垂足为C.若BD=8,BE=4,则AC=
.
三.解答题
16.如图,在Rt△ABC中,∠ACB=90°,BO平分∠ABC,交AC于点O,以O为圆心,OC为半径作圆,交OB于点E.
(1)求证:AB与⊙O相切;
(2)连接CE并延长,交AB于点F,若CF⊥AB,且CF=3,求⊙O的半径.
17.如图,△ABC外切于⊙O,切点分别为D、E、F,BC=7,⊙O的半径为,
(1)∠A=60°,求△ABC的周长.
(2)若∠A=70°,点M为⊙O上异于F、E的动点,则∠FME的度数为
°.
参考答案
1.D
2.B
3.C
4.B
5.B
6.B
7.C
8.B
9.D
10.A
11.1
12.25
13.M(4﹣,0)或(4+,0),
14.100°
15.9.6
16.(1)证明:作OD⊥AB于D,如图,
∵BO平分∠ABC,OC⊥BC,OD⊥AB,
∴OD=OC,
而OC为⊙O的半径,
∴AB与⊙O相切;
(2)作OH⊥CE于H,如图,设⊙O的半径为r,
易得四边形OHFD为矩形,
∴HF=OD=r,
∵OC=OE,OH⊥CE,
∴∠OCH=∠EOH,
∵OH∥BF,
∴∠CBO=∠BOH,
∵∠COH+∠BOH+∠CBO=90°,
∴∠COH=30°,
在Rt△OCH中,CH=CF﹣HF=3﹣r,
∵CH=OC,
∴3﹣r=r,解得r=2,
即⊙O的半径为2.
17.解:(1)连接OE、OF、OA,如图,
∵△ABC外切于⊙O,切点分别为D、E、F,
∴BD=BF,CD=CE,OE⊥AC,OF⊥AB,OA平分∠BAC,
∴∠OAE=×60°=30°,
∴AE=OE=×=3,
∴△ABC的周长=BC+BF+AF+AE+CE=BC+BD+CD+2AE=2BC+2AE=2×7+2×3=1=20;
(2)∵OE⊥AC,OF⊥AB,
∴∠OEA=∠OFA=90°,
∴∠EOF=180°﹣∠BAC=180°﹣70°=110°,
当点M在上时,如图,∠FME=∠EOF=55°;
当点M在上时,如图,∠FM′E=180°﹣55°=125°,
综上所述,∠FME的度数为55°或125°.
故答案为55或125.
同课章节目录
