华东师大版九年级数学上册 23.3.2相似三角形的判定 同步练习(Word版 含解析)
文档属性
| 名称 | 华东师大版九年级数学上册 23.3.2相似三角形的判定 同步练习(Word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 11:03:12 | ||
图片预览


文档简介
23.3.2相似三角形的判定
同步练习
一.选择题
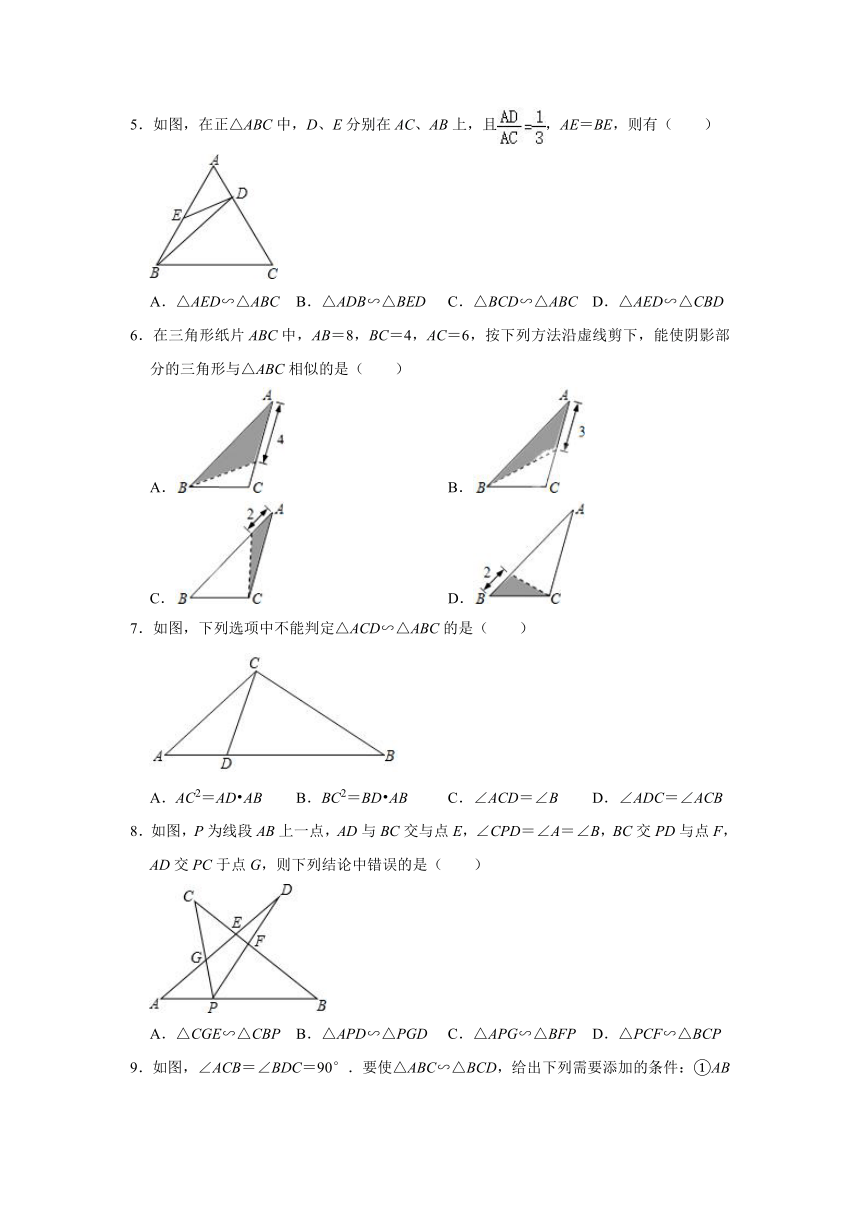
1.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB
B.△ANC∽△AMB
C.△ANC∽△ACM
D.△CMN∽△BCA
2.如图,网格中每个小正方形的边长均为1,则图中与阴影三角形相似的三角形是( )
A.A
B.B
C.C
D.D
3.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B
B.∠APC=∠ACB
C.AP:AC=AC:AB
D.AP:AB=PC:BC
4.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
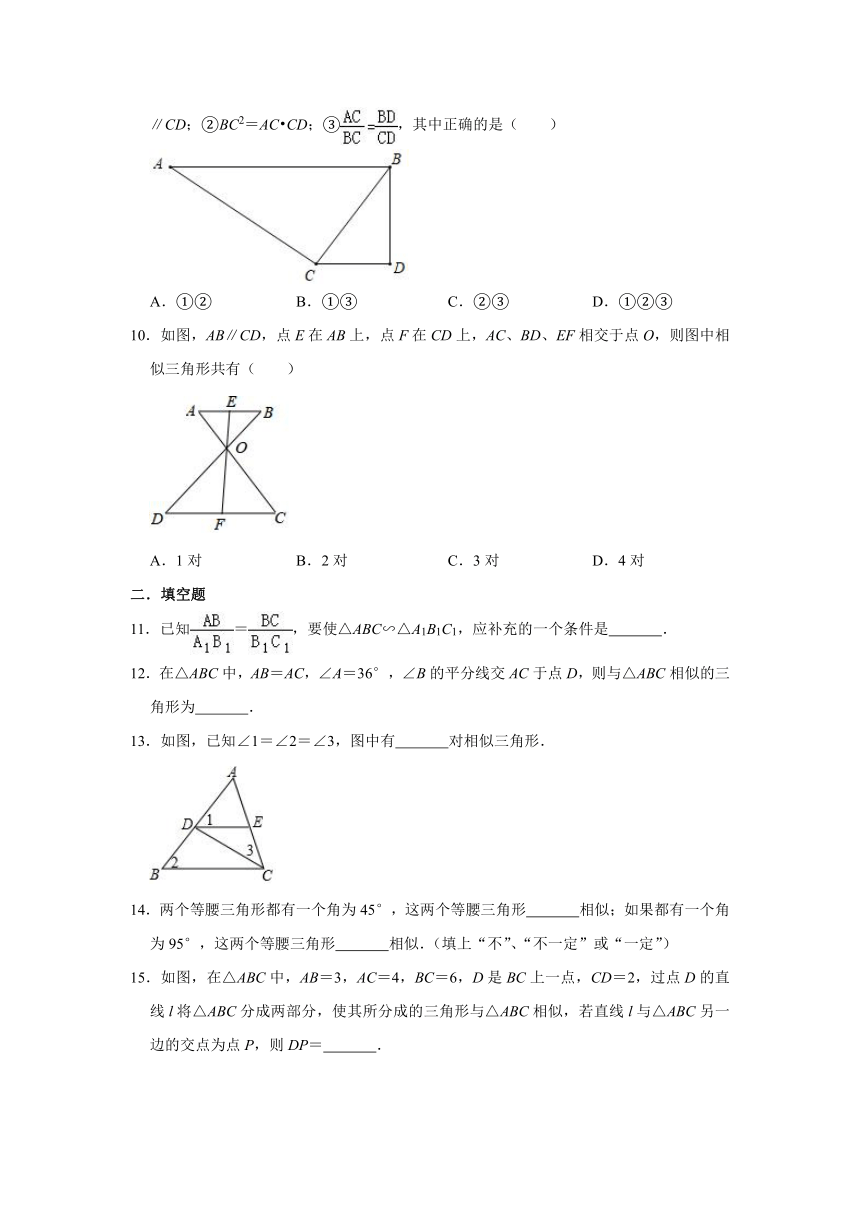
5.如图,在正△ABC中,D、E分别在AC、AB上,且,AE=BE,则有( )
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
6.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
A.
B.
C.
D.
7.如图,下列选项中不能判定△ACD∽△ABC的是( )
A.AC2=AD?AB
B.BC2=BD?AB
C.∠ACD=∠B
D.∠ADC=∠ACB
8.如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP
B.△APD∽△PGD
C.△APG∽△BFP
D.△PCF∽△BCP
9.如图,∠ACB=∠BDC=90°.要使△ABC∽△BCD,给出下列需要添加的条件:①AB∥CD;②BC2=AC?CD;③,其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
10.如图,AB∥CD,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有( )
A.1对
B.2对
C.3对
D.4对
二.填空题
11.已知=,要使△ABC∽△A1B1C1,应补充的一个条件是
.
12.在△ABC中,AB=AC,∠A=36°,∠B的平分线交AC于点D,则与△ABC相似的三角形为
.
13.如图,已知∠1=∠2=∠3,图中有
对相似三角形.
14.两个等腰三角形都有一个角为45°,这两个等腰三角形
相似;如果都有一个角为95°,这两个等腰三角形
相似.(填上“不”、“不一定”或“一定”)
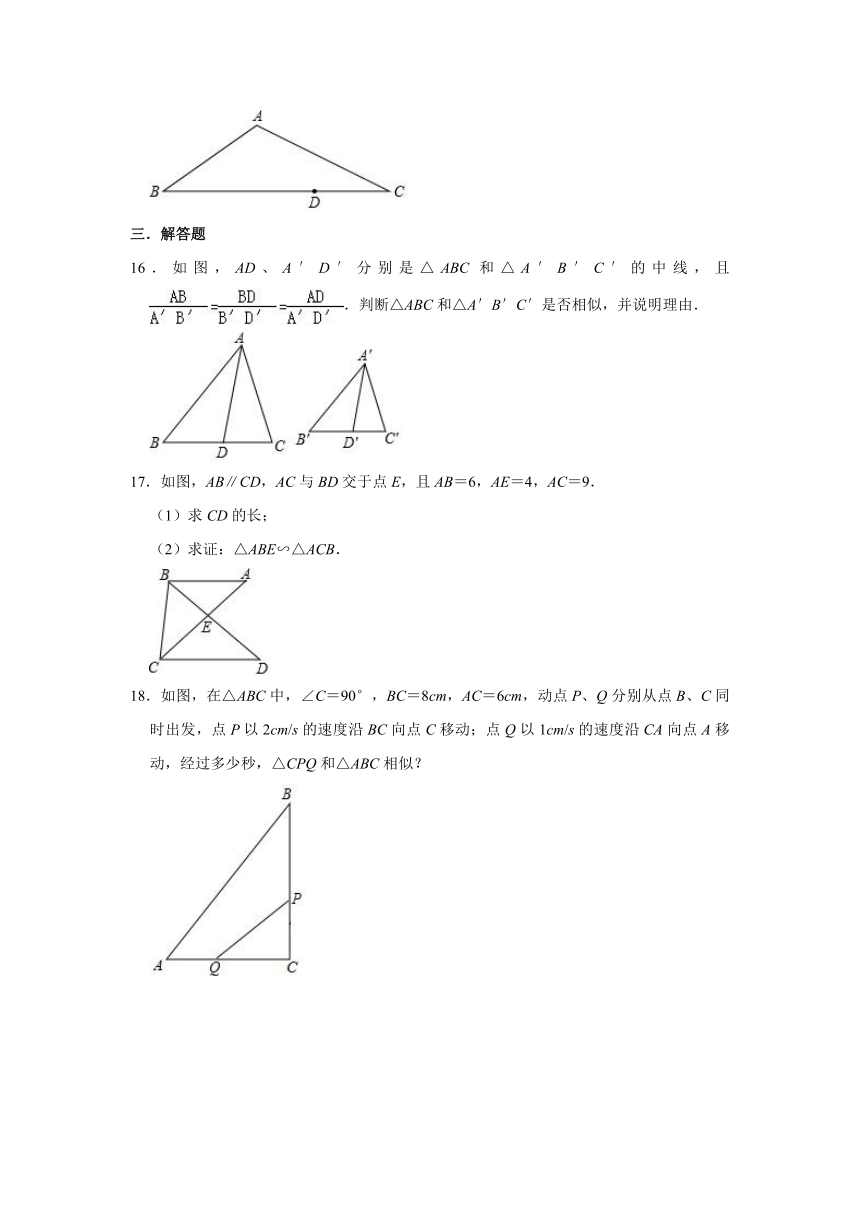
15.如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为点P,则DP=
.
三.解答题
16.如图,AD、A′D′分别是△ABC和△A′B′C′的中线,且.判断△ABC和△A′B′C′是否相似,并说明理由.
17.如图,AB∥CD,AC与BD交于点E,且AB=6,AE=4,AC=9.
(1)求CD的长;
(2)求证:△ABE∽△ACB.
18.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,动点P、Q分别从点B、C同时出发,点P以2cm/s的速度沿BC向点C移动;点Q以1cm/s的速度沿CA向点A移动,经过多少秒,△CPQ和△ABC相似?
参考答案
1.解:∵CM=CN
∴∠CNM=∠CMN
∵∠CNA=∠CMN+∠MCN,∠AMB=∠CNM+∠MCN
∴∠CNA=∠AMB
∵AM:AN=BM:CM
∴AM:AN=BM:CN
∴△ANC∽△AMB
故选:B.
2.解:黑色三角形两直角边长分别为2和3,
(A)该直角三角形的两直角边长分别为3和4,且≠,故不能与阴影三角形相似.
(B)该直角三角形的两直角边长分别为4和5,且,故不能与阴影三角形相似.
(C)该直角三角形的两直角边长分别为4和6,且=,故能与阴影三角形相似.
(D)该三角形的三边长分别为和、、,不是直角三角形,故不能与阴影三角形相似.
故选:C.
3.解:A、当∠ACP=∠B,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
C、当AP:AC=AC:AB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
D、当AP:AB=PC:BC,∠A=∠A,无法证明△APC∽△ACB,故该选项符合题意;
故选:D.
4.解:A、相似:∵∠A=55°∴∠B=90°﹣55°=35°∵∠D=35°∴∠B=∠D∵∠C=∠F∴△ABC∽△DEF;
B、相似:∵AC=9,BC=12,DF=6,EF=8,∴,∵∠C=∠F∴△ABC∽△DEF;
C、有一组角相等两边对应成比例,但该组角不是这两边的夹角,故不相似;
D、相似:由题意AB=10,AC=8,可得BC=6,∵DE=15,EF=9,∴,∵∠B=∠E,∴△ABC∽△DEF;
故选:C.
5.解:∵△ABC是等边三角形,=,
∴AB=BC=AC,∠A=∠C,
设AD=x,AC=3x,
则BC=3x,CD=2x,
∵AE=BE=x,
∴,,
∴,
∴△AED∽△CBD;
故选:D.
6.解:三角形纸片ABC中,AB=8,BC=4,AC=6.
A、==,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B、=,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
C、==,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、==,对应边===,则沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
故选:D.
7.解:A、∵AC2=AD?AB,
∴=,
∵∠A=∠A,
∴△ACD∽△ABC,故本选项不符合题意;
B、∵BC2=BD?AB,
∴=,
添加∠A=∠A,不能推出△ACD∽△ABC,故本选项符合题意;
C、∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC,故本选项不符合题意;
D、∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC,故本选项不符合题意;
故选:B.
8.解:∵∠CPD=∠A=∠B,且∠APD=∠B+∠PFB=∠APC+∠CPD,
∴∠APC=∠BFP,且∠A=∠B,
∴△APG∽△BFP,故选项C不合题意,
∵∠A=∠CPD,∠D=∠D,
∴△APD∽△PGD,故选项B不合题意,
∵∠B=∠CPD,∠C=∠C,
∴△PCF∽△BCP,故选项D不合题意,
由条件无法证明△CGE∽△CBP,
故选项A符合题意,
故选:A.
9.解:①若AB∥CD,
∴∠ABC=∠BCD,且∠ACB=∠BDC=90°,
∴△ABC∽△BCD,故①符合题意;
②若BC2=AC?CD,
∴,且∠ACB=∠BDC=90°,
无法判定△ABC∽△BCD,故②不符合题意;
③若,且∠ACB=∠BDC=90°,
∴△ABC∽△BCD,故③符合题意;
故选:B.
10.解:∵AB∥CD,
∴△AEO∽△CFO,△BEO∽△DFO,△ABO∽△CDO,
故选:C.
11.解:已知=,要使△ABC∽△A1B1C1,应补充的一个条件是∠B=∠B1.
故答案为:∠B=∠B1.
12.解:如图,∵AB=AC,
∴∠ABC=∠C,
∵∠A=36°,
∴∠ABC=∠C=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABC=36°,
∴∠CBD=∠A,
而∠BCD=∠ACB,
∴△BCD∽△ABC.
故答案为△BCD.
13.解:∵∠A=∠A,∠1=∠2,
∴∠ADE∽△ABC,
∵∠A=∠A,
∠1=∠3,
∴△ADE∽△ACD,
∴△ABC∽△ACD,
∵∠1=∠2,
∴DE∥BC,
∴∠EDC=∠DCB,
∴DE∥CB,
∴∠DCB=∠CDE,
∵∠2=∠3,
∴△BDC∽△CED,
故答案为4
14.解:由于45°是锐角,可以作等腰三角形的顶角或底角,故不一定相似;
根据三角形的内角和定理:等于95°的角只能是顶角,
即△ABC和△DEF的顶角∠A=∠D=95°,
∵AB=AC,DE=DF,
∴∠B=∠C=(180°﹣∠A)=42.5°,∠E=∠F=(180°﹣∠D)=42.5°,
∴∠B=∠E,
∵∠A=∠D,
∴△ABC∽△DEF.
故答案是:不一定;一定.
15.解:如图1,若DP∥AB,
∴△CDP∽△CBA,
∴,
∴
∴DP=1;
如图2,若DP∥AC,
∴△BDP∽△BCA,
∴,
∴
∴PD=;
如图3,若∠CPD=∠B,且∠C=∠C,
∴△CDP∽△CAB,
∴,
∴,
∴PD=,
故答案为:1或或.
16.解:△ABC∽△A'B'C',
理由:∵
∴△ABD∽△A'B'D',
∴∠B=∠B',
∵AD、A'D'分别是△ABC和△A'B'C'的中线
∴,,
∴,
在△ABC和△A'B'C'中
∵,且∠B=∠B'
∴△ABC∽△A'B'C'.
17.(1)解:∵AE=4,AC=9
∴CE=AC﹣AE=9﹣4=5;
∵AB∥CD,
∴△CDE∽△ABE;
∴=,
∴CD===,
(2)证明:∵==,==
∴=,
∵∠A=∠A,
∴△ABE∽△ACB;
18.解:设经过t秒,则BP=2t,CQ=t,
∴PC=8﹣2t,
∵∠QCP=∠ACB,
∴当△CPQ∽△CBA时,
有,
即,
解得t=2.4.
当△CPQ∽△CAB,
∴,
即,
解得t=.
综上,经过2.4或秒.
同步练习
一.选择题
1.如图,点M在BC上,点N在AM上,CM=CN,,下列结论正确的是( )
A.△ABM∽△ACB
B.△ANC∽△AMB
C.△ANC∽△ACM
D.△CMN∽△BCA
2.如图,网格中每个小正方形的边长均为1,则图中与阴影三角形相似的三角形是( )
A.A
B.B
C.C
D.D
3.如图,在△ABC中,点P为AB上一点连接CP.若再添加一个条件使△APC与△ACB相似,则下列选项中不能作为添加条件的是( )
A.∠ACP=∠B
B.∠APC=∠ACB
C.AP:AC=AC:AB
D.AP:AB=PC:BC
4.在Rt△ABC和Rt△DEF中,∠C=∠F=90°,下列条件中不能判定这两个三角形相似的是( )
A.∠A=55°,∠D=35°
B.AC=9,BC=12,DF=6,EF=8
C.AC=3,BC=4,DF=6,DE=8
D.AB=10,AC=8,DE=15,EF=9
5.如图,在正△ABC中,D、E分别在AC、AB上,且,AE=BE,则有( )
A.△AED∽△ABC
B.△ADB∽△BED
C.△BCD∽△ABC
D.△AED∽△CBD
6.在三角形纸片ABC中,AB=8,BC=4,AC=6,按下列方法沿虚线剪下,能使阴影部分的三角形与△ABC相似的是( )
A.
B.
C.
D.
7.如图,下列选项中不能判定△ACD∽△ABC的是( )
A.AC2=AD?AB
B.BC2=BD?AB
C.∠ACD=∠B
D.∠ADC=∠ACB
8.如图,P为线段AB上一点,AD与BC交与点E,∠CPD=∠A=∠B,BC交PD与点F,AD交PC于点G,则下列结论中错误的是( )
A.△CGE∽△CBP
B.△APD∽△PGD
C.△APG∽△BFP
D.△PCF∽△BCP
9.如图,∠ACB=∠BDC=90°.要使△ABC∽△BCD,给出下列需要添加的条件:①AB∥CD;②BC2=AC?CD;③,其中正确的是( )
A.①②
B.①③
C.②③
D.①②③
10.如图,AB∥CD,点E在AB上,点F在CD上,AC、BD、EF相交于点O,则图中相似三角形共有( )
A.1对
B.2对
C.3对
D.4对
二.填空题
11.已知=,要使△ABC∽△A1B1C1,应补充的一个条件是
.
12.在△ABC中,AB=AC,∠A=36°,∠B的平分线交AC于点D,则与△ABC相似的三角形为
.
13.如图,已知∠1=∠2=∠3,图中有
对相似三角形.
14.两个等腰三角形都有一个角为45°,这两个等腰三角形
相似;如果都有一个角为95°,这两个等腰三角形
相似.(填上“不”、“不一定”或“一定”)
15.如图,在△ABC中,AB=3,AC=4,BC=6,D是BC上一点,CD=2,过点D的直线l将△ABC分成两部分,使其所分成的三角形与△ABC相似,若直线l与△ABC另一边的交点为点P,则DP=
.
三.解答题
16.如图,AD、A′D′分别是△ABC和△A′B′C′的中线,且.判断△ABC和△A′B′C′是否相似,并说明理由.
17.如图,AB∥CD,AC与BD交于点E,且AB=6,AE=4,AC=9.
(1)求CD的长;
(2)求证:△ABE∽△ACB.
18.如图,在△ABC中,∠C=90°,BC=8cm,AC=6cm,动点P、Q分别从点B、C同时出发,点P以2cm/s的速度沿BC向点C移动;点Q以1cm/s的速度沿CA向点A移动,经过多少秒,△CPQ和△ABC相似?
参考答案
1.解:∵CM=CN
∴∠CNM=∠CMN
∵∠CNA=∠CMN+∠MCN,∠AMB=∠CNM+∠MCN
∴∠CNA=∠AMB
∵AM:AN=BM:CM
∴AM:AN=BM:CN
∴△ANC∽△AMB
故选:B.
2.解:黑色三角形两直角边长分别为2和3,
(A)该直角三角形的两直角边长分别为3和4,且≠,故不能与阴影三角形相似.
(B)该直角三角形的两直角边长分别为4和5,且,故不能与阴影三角形相似.
(C)该直角三角形的两直角边长分别为4和6,且=,故能与阴影三角形相似.
(D)该三角形的三边长分别为和、、,不是直角三角形,故不能与阴影三角形相似.
故选:C.
3.解:A、当∠ACP=∠B,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
B、当∠APC=∠ACB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
C、当AP:AC=AC:AB,∠A=∠A,可得△APC∽△ACB,故该选项不符合题意;
D、当AP:AB=PC:BC,∠A=∠A,无法证明△APC∽△ACB,故该选项符合题意;
故选:D.
4.解:A、相似:∵∠A=55°∴∠B=90°﹣55°=35°∵∠D=35°∴∠B=∠D∵∠C=∠F∴△ABC∽△DEF;
B、相似:∵AC=9,BC=12,DF=6,EF=8,∴,∵∠C=∠F∴△ABC∽△DEF;
C、有一组角相等两边对应成比例,但该组角不是这两边的夹角,故不相似;
D、相似:由题意AB=10,AC=8,可得BC=6,∵DE=15,EF=9,∴,∵∠B=∠E,∴△ABC∽△DEF;
故选:C.
5.解:∵△ABC是等边三角形,=,
∴AB=BC=AC,∠A=∠C,
设AD=x,AC=3x,
则BC=3x,CD=2x,
∵AE=BE=x,
∴,,
∴,
∴△AED∽△CBD;
故选:D.
6.解:三角形纸片ABC中,AB=8,BC=4,AC=6.
A、==,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B、=,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
C、==,对应边==≠,则沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
D、==,对应边===,则沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
故选:D.
7.解:A、∵AC2=AD?AB,
∴=,
∵∠A=∠A,
∴△ACD∽△ABC,故本选项不符合题意;
B、∵BC2=BD?AB,
∴=,
添加∠A=∠A,不能推出△ACD∽△ABC,故本选项符合题意;
C、∵∠A=∠A,∠ACD=∠B,
∴△ACD∽△ABC,故本选项不符合题意;
D、∵∠A=∠A,∠ADC=∠ACB,
∴△ACD∽△ABC,故本选项不符合题意;
故选:B.
8.解:∵∠CPD=∠A=∠B,且∠APD=∠B+∠PFB=∠APC+∠CPD,
∴∠APC=∠BFP,且∠A=∠B,
∴△APG∽△BFP,故选项C不合题意,
∵∠A=∠CPD,∠D=∠D,
∴△APD∽△PGD,故选项B不合题意,
∵∠B=∠CPD,∠C=∠C,
∴△PCF∽△BCP,故选项D不合题意,
由条件无法证明△CGE∽△CBP,
故选项A符合题意,
故选:A.
9.解:①若AB∥CD,
∴∠ABC=∠BCD,且∠ACB=∠BDC=90°,
∴△ABC∽△BCD,故①符合题意;
②若BC2=AC?CD,
∴,且∠ACB=∠BDC=90°,
无法判定△ABC∽△BCD,故②不符合题意;
③若,且∠ACB=∠BDC=90°,
∴△ABC∽△BCD,故③符合题意;
故选:B.
10.解:∵AB∥CD,
∴△AEO∽△CFO,△BEO∽△DFO,△ABO∽△CDO,
故选:C.
11.解:已知=,要使△ABC∽△A1B1C1,应补充的一个条件是∠B=∠B1.
故答案为:∠B=∠B1.
12.解:如图,∵AB=AC,
∴∠ABC=∠C,
∵∠A=36°,
∴∠ABC=∠C=(180°﹣36°)=72°,
∵BD平分∠ABC,
∴∠CBD=∠ABC=36°,
∴∠CBD=∠A,
而∠BCD=∠ACB,
∴△BCD∽△ABC.
故答案为△BCD.
13.解:∵∠A=∠A,∠1=∠2,
∴∠ADE∽△ABC,
∵∠A=∠A,
∠1=∠3,
∴△ADE∽△ACD,
∴△ABC∽△ACD,
∵∠1=∠2,
∴DE∥BC,
∴∠EDC=∠DCB,
∴DE∥CB,
∴∠DCB=∠CDE,
∵∠2=∠3,
∴△BDC∽△CED,
故答案为4
14.解:由于45°是锐角,可以作等腰三角形的顶角或底角,故不一定相似;
根据三角形的内角和定理:等于95°的角只能是顶角,
即△ABC和△DEF的顶角∠A=∠D=95°,
∵AB=AC,DE=DF,
∴∠B=∠C=(180°﹣∠A)=42.5°,∠E=∠F=(180°﹣∠D)=42.5°,
∴∠B=∠E,
∵∠A=∠D,
∴△ABC∽△DEF.
故答案是:不一定;一定.
15.解:如图1,若DP∥AB,
∴△CDP∽△CBA,
∴,
∴
∴DP=1;
如图2,若DP∥AC,
∴△BDP∽△BCA,
∴,
∴
∴PD=;
如图3,若∠CPD=∠B,且∠C=∠C,
∴△CDP∽△CAB,
∴,
∴,
∴PD=,
故答案为:1或或.
16.解:△ABC∽△A'B'C',
理由:∵
∴△ABD∽△A'B'D',
∴∠B=∠B',
∵AD、A'D'分别是△ABC和△A'B'C'的中线
∴,,
∴,
在△ABC和△A'B'C'中
∵,且∠B=∠B'
∴△ABC∽△A'B'C'.
17.(1)解:∵AE=4,AC=9
∴CE=AC﹣AE=9﹣4=5;
∵AB∥CD,
∴△CDE∽△ABE;
∴=,
∴CD===,
(2)证明:∵==,==
∴=,
∵∠A=∠A,
∴△ABE∽△ACB;
18.解:设经过t秒,则BP=2t,CQ=t,
∴PC=8﹣2t,
∵∠QCP=∠ACB,
∴当△CPQ∽△CBA时,
有,
即,
解得t=2.4.
当△CPQ∽△CAB,
∴,
即,
解得t=.
综上,经过2.4或秒.
