人教版八年级数学上册 13.2 画轴对称图形 同步课时练习(word版 含答案)
文档属性
| 名称 | 人教版八年级数学上册 13.2 画轴对称图形 同步课时练习(word版 含答案) | 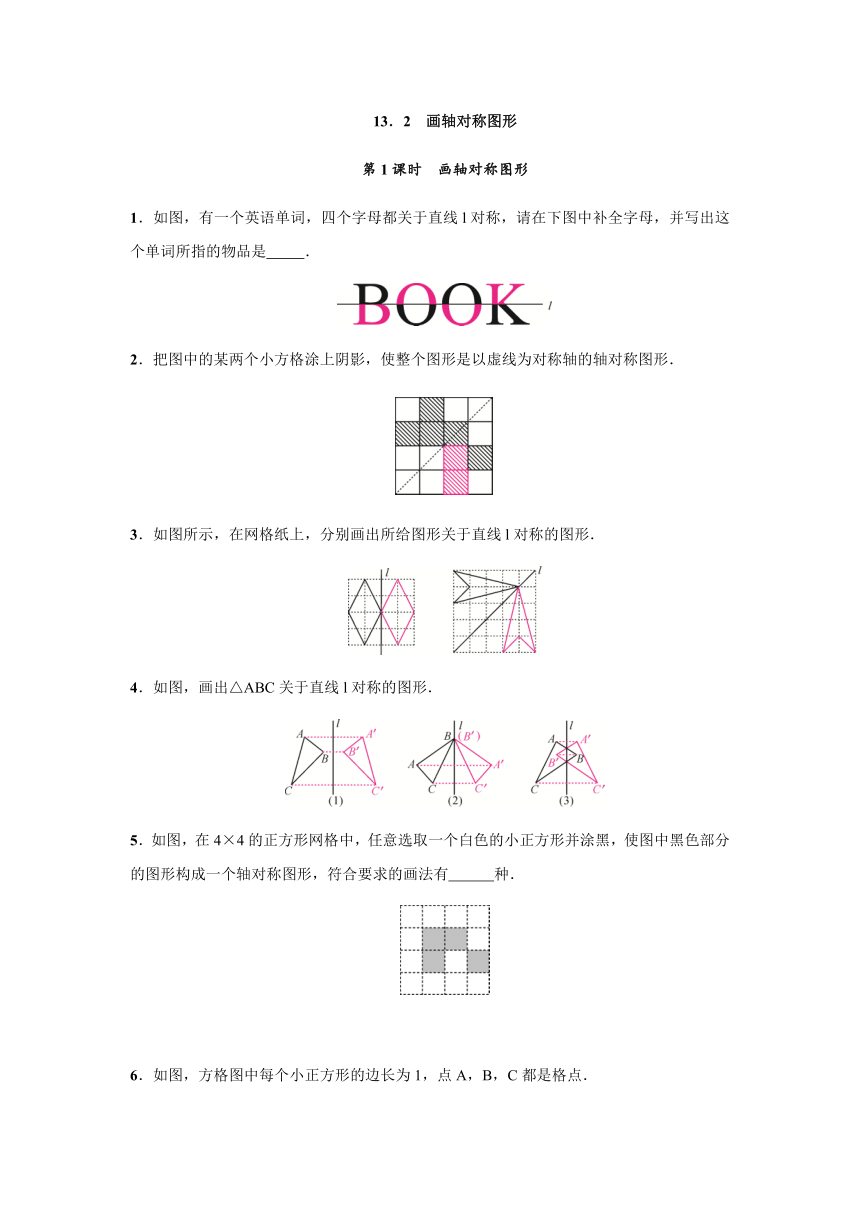 | |
| 格式 | zip | ||
| 文件大小 | 625.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 15:15:22 | ||
图片预览




文档简介
13.2 画轴对称图形
第1课时 画轴对称图形
1.如图,有一个英语单词,四个字母都关于直线l对称,请在下图中补全字母,并写出这个单词所指的物品是
.
2.把图中的某两个小方格涂上阴影,使整个图形是以虚线为对称轴的轴对称图形.
3.如图所示,在网格纸上,分别画出所给图形关于直线l对称的图形.
4.如图,画出△ABC关于直线l对称的图形.
5.如图,在4×4的正方形网格中,任意选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形,符合要求的画法有
种.
6.如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
7.如图,在10×10的正方形的网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
第2课时 用坐标表示轴对称
1.在平面直角坐标系中,点P(3,-2)关于y轴的对称点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.在平面直角坐标系中,点B的坐标是(4,-1),点A与点B关于x轴对称,则点A的坐标是(
)
A.(4,1)
B.(-1,4)
C.(-4,-1)
D.(-1,-4)
3.在平面直角坐标系中,点A(2,3)与点B关于y轴对称,则点B的坐标为(
)
A.(-2,3)
B.(-2,-3)
C.(2,-3)
D.(-3,-2)
4.点E(a,-5)与点F(-2,b)关于y轴对称,则a=
,b=
.
5.点M(-2,1)关于x轴对称的点N的坐标是
,直线MN与x轴的位置关系是
.
6.分别写出下列各点关于x轴和y轴对称的点的坐标:(2,3),(-2,4),(-3,-3),(2,0),(0,-3).
7.已知点A(a+2b,1),B(-2,2a-b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求a+b的值.
8.如图,△ABO关于x轴对称,点A的坐标为(1,-2),则点B的坐标为(
)
A.(-1,2)
B.(-1,-2)
C.(1,2)
D.(-2,1)
第8题图
第9题图
9.已知正方形ABCD在坐标轴上的位置如图所示,x轴、y轴分别是正方形的两条对称轴,若A(2,2),则点B的坐标为
,点C的坐标为
,点D的坐标为
.
10.如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1.
11.点P(1,2)关于直线y=1对称的点的坐标是
;关于直线x=2对称的点的坐标是
.
12.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为(
)
A.(-3,-2)
B.(2,2)
C.(-2,2)
D.(2,-2)
13.在平面直角坐标系中,已知点A(-2,4)关于x轴对称的点为B,点B关于y轴对称的点为C,则点C的坐标是(
)
A.(2,-4)
B.(-4,
2)
C.(2,4)
D.(-2,4)
14.在平面直角坐标系内,点A(x-6,2y+1)与点B(2x,y-1)关于y轴对称,则x+y的值为(
)
A.0
B.-1
C.2
D.-3
15.点P(3a+6,3-a)关于x轴的对称点在第四象限内,则a的取值范围为
.
16.如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,写出△ABC关于x轴对称的△A2B2C2的各点坐标.
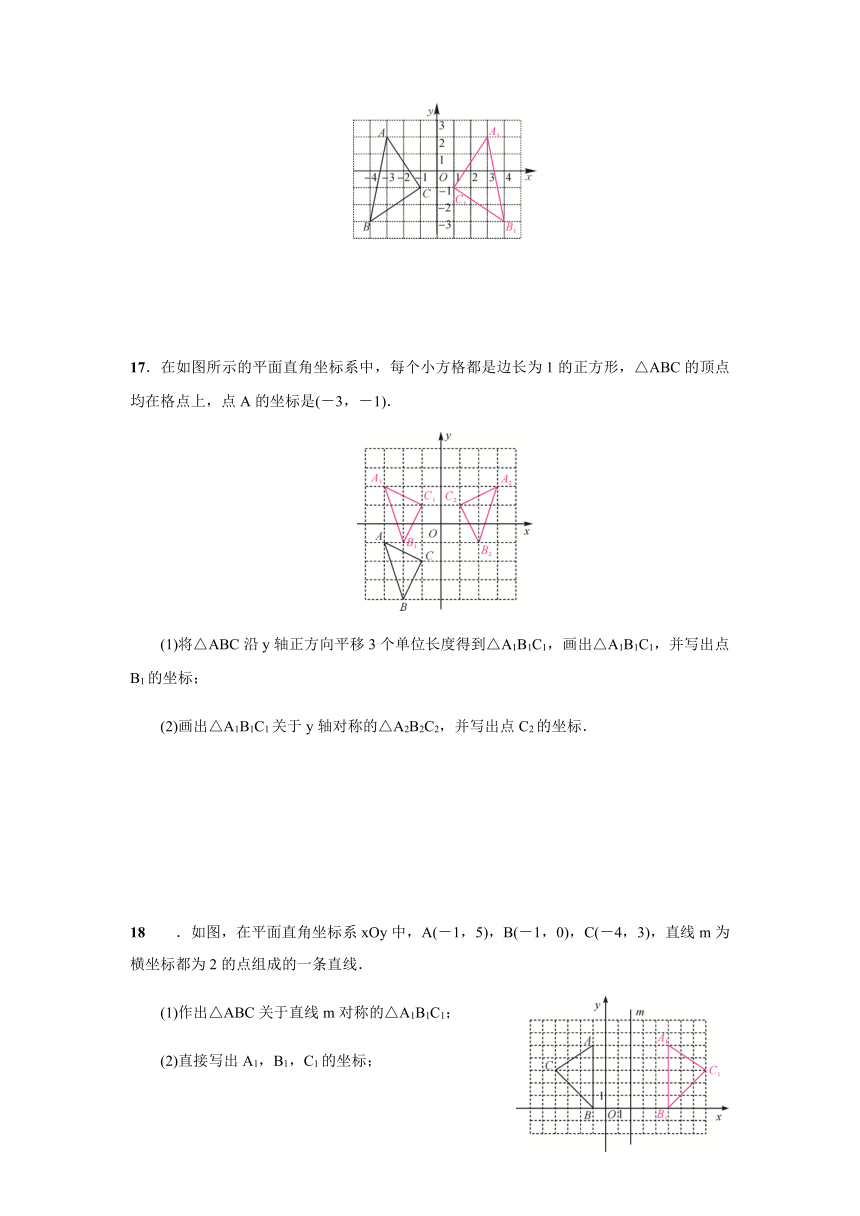
17.在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).
(1)将△ABC沿y轴正方向平移3个单位长度得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
18.如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),直线m为横坐标都为2的点组成的一条直线.
(1)作出△ABC关于直线m对称的△A1B1C1;
(2)直接写出A1,B1,C1的坐标;
(3)求出△A1B1C1的面积.
参考答案:
13.2 画轴对称图形
第1课时 画轴对称图形
1.书.
2.
解:如图.
3.
解:如图.
4.
解:如图所示.
5.2.
6.
解:(1)如图所示,△A1B1C1即为所求.
(2)由图可得,AA1=10.
7.
解:(1)如图所示.
(2)S四边形BB1C1C=×(2+4)×4
=12.
第2课时 用坐标表示轴对称
1.C
2.A
3.A
4.
2,
-5.
5.
(-2,-1),
垂直.
6.
解:各点关于x轴的对称的点的坐标分别是(2,-3),(-2,-4),(-3,3),(2,0),(0,3);
关于y轴的对称的点的坐标分别是(-2,3),(2,4),(3,-3),(-2,0),(0,-3).
7.解:(1)由题意,得
解得
(2)由题意,得
解得
∴a+b=.
C
(2,-2),
(-2,-2),
(-2,2).
10.
解:
(1)AB=5,AB边上的高是3,则S△ABC=×5×3=.
(2)如图.
11.
(1,0);
(3,2).
12.B
13.A
14.A
15.
-2<a<3.
16.
解:△ABC的各顶点的坐标分别为:A(-3,2),B(-4,-3),C(-1,-1),△A1B1C1如图所示.
△A2B2C2的各点坐标分别为:A2(-3,-2),B2(-4,3),C2(-1,1).
17.
解:(1)如图所示,△A1B1C1即为所求,点B1的坐标为(-2,-1).
(2)如图所示,△A2B2C2即为所求,点C2的坐标为(1,1).
18.
解:(1)如图所示.
(2)A1(5,5),B1(5,0),C1(8,3).
(3)△A1B1C1的面积为7.5.
第1课时 画轴对称图形
1.如图,有一个英语单词,四个字母都关于直线l对称,请在下图中补全字母,并写出这个单词所指的物品是
.
2.把图中的某两个小方格涂上阴影,使整个图形是以虚线为对称轴的轴对称图形.
3.如图所示,在网格纸上,分别画出所给图形关于直线l对称的图形.
4.如图,画出△ABC关于直线l对称的图形.
5.如图,在4×4的正方形网格中,任意选取一个白色的小正方形并涂黑,使图中黑色部分的图形构成一个轴对称图形,符合要求的画法有
种.
6.如图,方格图中每个小正方形的边长为1,点A,B,C都是格点.
(1)画出△ABC关于直线BM对称的△A1B1C1;
(2)写出AA1的长度.
7.如图,在10×10的正方形的网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
(1)在图中作出△ABC关于直线l对称的△A1B1C1;
(2)在(1)问的结果下,连接BB1,CC1,求四边形BB1C1C的面积.
第2课时 用坐标表示轴对称
1.在平面直角坐标系中,点P(3,-2)关于y轴的对称点在(
)
A.第一象限
B.第二象限
C.第三象限
D.第四象限
2.在平面直角坐标系中,点B的坐标是(4,-1),点A与点B关于x轴对称,则点A的坐标是(
)
A.(4,1)
B.(-1,4)
C.(-4,-1)
D.(-1,-4)
3.在平面直角坐标系中,点A(2,3)与点B关于y轴对称,则点B的坐标为(
)
A.(-2,3)
B.(-2,-3)
C.(2,-3)
D.(-3,-2)
4.点E(a,-5)与点F(-2,b)关于y轴对称,则a=
,b=
.
5.点M(-2,1)关于x轴对称的点N的坐标是
,直线MN与x轴的位置关系是
.
6.分别写出下列各点关于x轴和y轴对称的点的坐标:(2,3),(-2,4),(-3,-3),(2,0),(0,-3).
7.已知点A(a+2b,1),B(-2,2a-b).
(1)若点A,B关于x轴对称,求a,b的值;
(2)若点A,B关于y轴对称,求a+b的值.
8.如图,△ABO关于x轴对称,点A的坐标为(1,-2),则点B的坐标为(
)
A.(-1,2)
B.(-1,-2)
C.(1,2)
D.(-2,1)
第8题图
第9题图
9.已知正方形ABCD在坐标轴上的位置如图所示,x轴、y轴分别是正方形的两条对称轴,若A(2,2),则点B的坐标为
,点C的坐标为
,点D的坐标为
.
10.如图,在平面直角坐标系中,A(-1,5),B(-1,0),C(-4,3).
(1)求出△ABC的面积;
(2)在图中作出△ABC关于y轴的对称图形△A1B1C1.
11.点P(1,2)关于直线y=1对称的点的坐标是
;关于直线x=2对称的点的坐标是
.
12.在平面直角坐标系中,将点A(-1,-2)向右平移3个单位长度得到点B,则点B关于x轴的对称点B′的坐标为(
)
A.(-3,-2)
B.(2,2)
C.(-2,2)
D.(2,-2)
13.在平面直角坐标系中,已知点A(-2,4)关于x轴对称的点为B,点B关于y轴对称的点为C,则点C的坐标是(
)
A.(2,-4)
B.(-4,
2)
C.(2,4)
D.(-2,4)
14.在平面直角坐标系内,点A(x-6,2y+1)与点B(2x,y-1)关于y轴对称,则x+y的值为(
)
A.0
B.-1
C.2
D.-3
15.点P(3a+6,3-a)关于x轴的对称点在第四象限内,则a的取值范围为
.
16.如图,写出△ABC的各顶点坐标,并画出△ABC关于y轴对称的△A1B1C1,写出△ABC关于x轴对称的△A2B2C2的各点坐标.
17.在如图所示的平面直角坐标系中,每个小方格都是边长为1的正方形,△ABC的顶点均在格点上,点A的坐标是(-3,-1).
(1)将△ABC沿y轴正方向平移3个单位长度得到△A1B1C1,画出△A1B1C1,并写出点B1的坐标;
(2)画出△A1B1C1关于y轴对称的△A2B2C2,并写出点C2的坐标.
18.如图,在平面直角坐标系xOy中,A(-1,5),B(-1,0),C(-4,3),直线m为横坐标都为2的点组成的一条直线.
(1)作出△ABC关于直线m对称的△A1B1C1;
(2)直接写出A1,B1,C1的坐标;
(3)求出△A1B1C1的面积.
参考答案:
13.2 画轴对称图形
第1课时 画轴对称图形
1.书.
2.
解:如图.
3.
解:如图.
4.
解:如图所示.
5.2.
6.
解:(1)如图所示,△A1B1C1即为所求.
(2)由图可得,AA1=10.
7.
解:(1)如图所示.
(2)S四边形BB1C1C=×(2+4)×4
=12.
第2课时 用坐标表示轴对称
1.C
2.A
3.A
4.
2,
-5.
5.
(-2,-1),
垂直.
6.
解:各点关于x轴的对称的点的坐标分别是(2,-3),(-2,-4),(-3,3),(2,0),(0,3);
关于y轴的对称的点的坐标分别是(-2,3),(2,4),(3,-3),(-2,0),(0,-3).
7.解:(1)由题意,得
解得
(2)由题意,得
解得
∴a+b=.
C
(2,-2),
(-2,-2),
(-2,2).
10.
解:
(1)AB=5,AB边上的高是3,则S△ABC=×5×3=.
(2)如图.
11.
(1,0);
(3,2).
12.B
13.A
14.A
15.
-2<a<3.
16.
解:△ABC的各顶点的坐标分别为:A(-3,2),B(-4,-3),C(-1,-1),△A1B1C1如图所示.
△A2B2C2的各点坐标分别为:A2(-3,-2),B2(-4,3),C2(-1,1).
17.
解:(1)如图所示,△A1B1C1即为所求,点B1的坐标为(-2,-1).
(2)如图所示,△A2B2C2即为所求,点C2的坐标为(1,1).
18.
解:(1)如图所示.
(2)A1(5,5),B1(5,0),C1(8,3).
(3)△A1B1C1的面积为7.5.
