六年级上册数学一课一练-1.5圆的面积(一) 北师大版(2014秋)(含答案)
文档属性
| 名称 | 六年级上册数学一课一练-1.5圆的面积(一) 北师大版(2014秋)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 119.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 08:37:43 | ||
图片预览



文档简介
六年级上册数学一课一练-1.5圆的面积(一)
一、单选题
1.钟面上,分针和时针尖走过的轨迹都是一个圆,以下说法,正确的是(??? )
A.?这两个圆的圆心相同???????????????????????????????????????????B.?这两个圆的半径相同
C.?这两个圆的直径相同???????????????????????????????????????????D.?这两个圆的面积相同
2.甲、乙、丙三个小朋友用相同的正方形手工纸剪圆,甲剪了九个最大的圆,乙剪了四个最大的圆,丙剪了一个最大的圆,三个人剩下的手工纸相比,(???? )
A.?甲最多??????????????????????????????????????B.?乙最多??????????????????????????????????????C.?一样多
3.下面图形中阴影部分的面积与左图相等的有(??? )个。
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
二、判断题
4.半径是4厘米的圆,它的周长和面积相等。
5.直径为6厘米的圆,它的周长和面积相同.(?? )
6.圆越大圆周率越大,圆越小圆周率越小.( ??)
7.面积相等的两个圆,它们的周长也一定相等。(?? )
三、填空题
8.一个圆形桌面的直径是?2米,它的面积是________平方米。
9.一个半径是4厘米的半圆,周长是________厘米,面积是________平方厘米。
10.圆规两脚间的距离是4厘米,用它画成的圆的周长是________,面积是________.
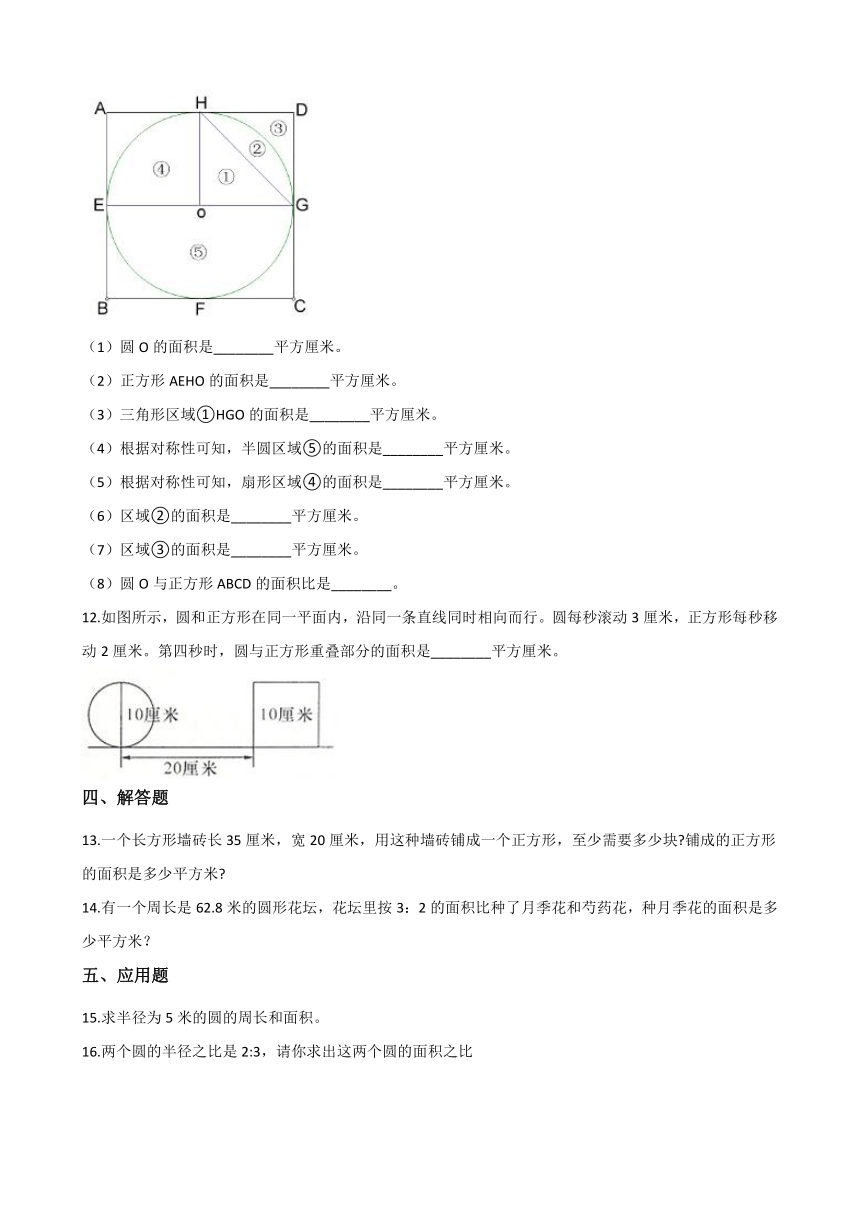
11.如图所示,已知正方形ABCD的边长为8厘米。π=3.14。
(1)圆O的面积是________平方厘米。
(2)正方形AEHO的面积是________平方厘米。
(3)三角形区域①HGO的面积是________平方厘米。
(4)根据对称性可知,半圆区域⑤的面积是________平方厘米。
(5)根据对称性可知,扇形区域④的面积是________平方厘米。
(6)区域②的面积是________平方厘米。
(7)区域③的面积是________平方厘米。
(8)圆O与正方形ABCD的面积比是________。
12.如图所示,圆和正方形在同一平面内,沿同一条直线同时相向而行。圆每秒滚动3厘米,正方形每秒移动2厘米。第四秒时,圆与正方形重叠部分的面积是________平方厘米。
四、解答题
13.一个长方形墙砖长35厘米,宽20厘米,用这种墙砖铺成一个正方形,至少需要多少块?铺成的正方形的面积是多少平方米?
14.有一个周长是62.8米的圆形花坛,花坛里按3:2的面积比种了月季花和芍药花,种月季花的面积是多少平方米?
五、应用题
15.求半径为5米的圆的周长和面积。
16.两个圆的半径之比是2:3,请你求出这两个圆的面积之比
参考答案
一、单选题
1.【答案】 A
【解析】【解答】 钟面上,分针和时针尖走过的轨迹都是一个圆,以下说法,正确的是:这两个圆的圆心相同。
故答案为:A。
【分析】钟面上,分针和时针尖走过的轨迹都是一个圆,这两个圆是同心圆,但是两根针的长短不相等,所以半径、直径和走过的面积都不相等,据此解答。
2.【答案】 C
【解析】【解答】设正方形的边长为a,
甲图中剩下部分的面积:
a×a-π()2×9
=a2-π××9
=a2-πa2
乙图中剩下部分的面积:
a×a-π()2×4
=a2-π××4
=a2-πa2
丙图中剩下部分的面积:
a×a-π()2
=a×a-π×
=a2-πa2
三个人剩下的手工纸同样多。
故答案为:C。
【分析】此题主要考查了圆和正方形面积的计算,观察图可知,设正方形的边长为a,正方形的面积=边长×边长,圆的面积:S=πr2 , 分别求出各图中剩下部分的面积,然后对比即可。
?
3.【答案】 D
【解析】【解答】 下面图形中阴影部分的面积与左图相等的有5个,
。
故答案为:D。
【分析】观察左图可知,阴影部分的面积=正方形的面积-空白圆的面积,后面几个图形的空白部分都可以转化成一个与左图大空白圆相等的面积,所以它们的阴影部分的面积都与左图相等。
二、判断题
4.【答案】 错误
【解析】【解答】解:周长和面积的意义不同,是不可能相等的。原题说法错误。
故答案为:错误。
【分析】半径为4厘米的圆的周长和面积的数字都是12.56,但是周长的单位是厘米,面积的单位是平方厘米,表示的意义是不同的。
5.【答案】 错误
【解析】【解答】解:周长与面积不能比较大小。
故答案为:错误。
【分析】周长与面积单位不同,不能进行大小比较。
6.【答案】 错误
【解析】【解答】圆周率π为定值,故错误.
故答案为:错误.
【分析】圆周率与圆的大小无关,圆周率为定值,即可做出判断.
7.【答案】 正确
【解析】【解答】解:面积相等的两个圆,它们的周长也一定相等。
故答案为:正确。
【分析】圆的面积=πr2 , 所以当圆的面积相等时,那么它们的半径相等,圆的周长=2πr,所以它们的周长也一定相等。
三、填空题
8.【答案】3.14
【解析】【解答】2÷2=1(米);
3.14×12
=3.14×1
=3.14(平方米).
故答案为:3.14 .
【分析】已知圆的直径,要求圆的面积,先求出圆的半径,圆的半径=直径÷2,然后用公式:S=πr2 , 据此求出圆的面积即可.
9.【答案】 20.56;25.12
【解析】【解答】半圆的周长:
3.14×4+2×4
=12.56+8
=20.56(厘米)
半圆的面积:
3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(平方厘米)
故答案为:20.56;25.12。
【分析】已知一个半圆的半径r,要求半圆的周长C半圆 , 用公式:C半圆=πr+2r,要求半圆的面积S半圆 , 用公式:S半圆=πr2÷2,据此列式解答。
10.【答案】 25.12厘米;50.24平方厘米
【解析】【解答】解:周长:3.14×4×2=25.12(厘米),面积:3.14×42=50.24(平方厘米)。
故答案为:25.12厘米;50.24平方厘米。
【分析】圆规两脚间的距离是所画圆的半径;圆的周长=2πr;圆的面积=πr2。据此代入数据作答即可。
11.【答案】 (1)50.24
(2)16
(3)8
(4)25.12
(5)12.56
(6)4.56
(7)3.44
(8)157:200
【解析】【解答】(1)8÷2=4(厘米);
3.14×42
=3.14×16
=50.24(平方厘米);
(2)8÷2=4(厘米);
正方形AEHO的面积是:4×4=16(平方厘米);
(3)三角形区域①HGO的面积是:4×4÷2=8(平方厘米);
(4)半圆区域⑤的面积是;50.24÷2=25.12(平方厘米);
(5)扇形区域④的面积是:3.14×42×
=3.14×16×
=50.24×
=12.56(平方厘米);
(6)区域②的面积是:12.56-8=4.56(平方厘米);
(7)区域③的面积是:16-12.56=3.44(平方厘米);
(8)圆O与正方形ABCD的面积比是:50.24:(8×8)=50.24:64=0.785:1.
故答案为:(1)50.24;(2)16;(3)8;(4)25.12;(5)12.56;(6)4.56;(7)3.44;(8)157:200.
【分析】(1)观察图形可知,正方形的边长是圆的直径,先求出圆的半径,用直径÷2=半径,然后用公式:S=πr2 , 据此求出圆的面积;
(2)要求正方形AEHO的面积,先求出它的边长,观察图可知,它的边长是圆的半径,根据正方形的面积=边长×边长,据此列式解答;
(3)三角形区域①HGO是一个等腰直角三角形,底和高都是圆的半径,依据三角形的面积公式:底×高÷2=三角形面积 ,据此列式解答;
(4)半圆区域⑤的面积等于圆O的面积的一半,用圆O的面积÷2=半圆区域⑤的面积,据此列式解答;
(5)要求扇形区域④的面积,用扇形的面积公式:S=, 据此列式解答;
(6)要求区域②的面积,根据对称性可知,区域①和②的面积和等于区域④的面积,所以用区域④的面积-区域①的面积=区域②的面积,据此列式解答;
(7)要求区域③的面积,根据对称性,用正方形AEHO的面积-区域④的面积=区域③的面积,据此列式解答;
(8)要求圆O与正方形ABCD的面积比是多少,用圆O的面积:正方形的面积,然后化简成最简整数比即可.
12.【答案】 39.25
【解析】【解答】解:第四秒时,圆与正方形重叠部分是半圆,所以面积为3.14×52÷2=39.25(平方厘米)。
故答案为:39.25。
【分析】从图中可以看出,第四秒时,两个图形一共走的距离=(3+2)×4=20厘米,此时圆心恰好与正方形的左边的边重合,所以重叠部分是半圆,面积为3.14×52÷2=39.25(平方厘米)。
四、解答题
13.【答案】 解:35=5×7
20=2×2×5
所以20和35的最小公倍数是:2×2×5×7=140
即正方形的边长最小是140厘米
140×140=19600(平方厘米)
19600平方厘米=1.96平方米
则地砖的块数为:140×140÷(35×20)
=19600÷700
=28(块)
答:至少要28块砖,铺成的正方形的面积是1.96平方米。
【解析】【分析】用长方形的墙砖铺成正方形,则这个正方形的边长是这个长方形长和宽的最小公倍数,先用短除法或分解质因数法求出35和20的最小公倍数,这个最小公倍数就是正方形的边长。再根据正方形面积公式:S=a×a,求出正方形的面积,并转换单位为平方米;最后,用“正方形面积÷长方形墙砖的面积=所需墙砖数量”,求出需要多少块墙砖。
14.【答案】 解:3.14×(62.8÷3.14÷2)2×
=3.14×102×
=314×
=188.4(平方米)
答:种月季花的面积是188.4平方米。
【解析】【分析】种月季花的面积占总面积的。先根据圆周长公式用周长除以3.14再除以2求出半径,然后根据圆面积公式计算花坛面积,再根据分数乘法的意义用圆面积乘种月季花占总面积的f分率即可求出种月季花的面积。
五、应用题
15.【答案】周长: (米);
面积: (平方米).
答:圆的周长是31.4米,面积是78.5平方米。
【解析】【分析】已知圆的半径,求圆的周长,用公式:C=2πr,求圆的面积,用公式:S=πr2 , 据此列式解答.
16.【答案】 圆的面积=半径的平方×π , 所以面积之比和半径的平方成正比,两个圆的面积之比为4:9。
【解析】【解答】圆的面积=半径的平方×π , 所以面积之比和半径的平方成正比
【分析】考察了学生认识和辨别正比例和反比例的能力
一、单选题
1.钟面上,分针和时针尖走过的轨迹都是一个圆,以下说法,正确的是(??? )
A.?这两个圆的圆心相同???????????????????????????????????????????B.?这两个圆的半径相同
C.?这两个圆的直径相同???????????????????????????????????????????D.?这两个圆的面积相同
2.甲、乙、丙三个小朋友用相同的正方形手工纸剪圆,甲剪了九个最大的圆,乙剪了四个最大的圆,丙剪了一个最大的圆,三个人剩下的手工纸相比,(???? )
A.?甲最多??????????????????????????????????????B.?乙最多??????????????????????????????????????C.?一样多
3.下面图形中阴影部分的面积与左图相等的有(??? )个。
A.?2???????????????????????????????????????????B.?3???????????????????????????????????????????C.?4???????????????????????????????????????????D.?5
二、判断题
4.半径是4厘米的圆,它的周长和面积相等。
5.直径为6厘米的圆,它的周长和面积相同.(?? )
6.圆越大圆周率越大,圆越小圆周率越小.( ??)
7.面积相等的两个圆,它们的周长也一定相等。(?? )
三、填空题
8.一个圆形桌面的直径是?2米,它的面积是________平方米。
9.一个半径是4厘米的半圆,周长是________厘米,面积是________平方厘米。
10.圆规两脚间的距离是4厘米,用它画成的圆的周长是________,面积是________.
11.如图所示,已知正方形ABCD的边长为8厘米。π=3.14。
(1)圆O的面积是________平方厘米。
(2)正方形AEHO的面积是________平方厘米。
(3)三角形区域①HGO的面积是________平方厘米。
(4)根据对称性可知,半圆区域⑤的面积是________平方厘米。
(5)根据对称性可知,扇形区域④的面积是________平方厘米。
(6)区域②的面积是________平方厘米。
(7)区域③的面积是________平方厘米。
(8)圆O与正方形ABCD的面积比是________。
12.如图所示,圆和正方形在同一平面内,沿同一条直线同时相向而行。圆每秒滚动3厘米,正方形每秒移动2厘米。第四秒时,圆与正方形重叠部分的面积是________平方厘米。
四、解答题
13.一个长方形墙砖长35厘米,宽20厘米,用这种墙砖铺成一个正方形,至少需要多少块?铺成的正方形的面积是多少平方米?
14.有一个周长是62.8米的圆形花坛,花坛里按3:2的面积比种了月季花和芍药花,种月季花的面积是多少平方米?
五、应用题
15.求半径为5米的圆的周长和面积。
16.两个圆的半径之比是2:3,请你求出这两个圆的面积之比
参考答案
一、单选题
1.【答案】 A
【解析】【解答】 钟面上,分针和时针尖走过的轨迹都是一个圆,以下说法,正确的是:这两个圆的圆心相同。
故答案为:A。
【分析】钟面上,分针和时针尖走过的轨迹都是一个圆,这两个圆是同心圆,但是两根针的长短不相等,所以半径、直径和走过的面积都不相等,据此解答。
2.【答案】 C
【解析】【解答】设正方形的边长为a,
甲图中剩下部分的面积:
a×a-π()2×9
=a2-π××9
=a2-πa2
乙图中剩下部分的面积:
a×a-π()2×4
=a2-π××4
=a2-πa2
丙图中剩下部分的面积:
a×a-π()2
=a×a-π×
=a2-πa2
三个人剩下的手工纸同样多。
故答案为:C。
【分析】此题主要考查了圆和正方形面积的计算,观察图可知,设正方形的边长为a,正方形的面积=边长×边长,圆的面积:S=πr2 , 分别求出各图中剩下部分的面积,然后对比即可。
?
3.【答案】 D
【解析】【解答】 下面图形中阴影部分的面积与左图相等的有5个,
。
故答案为:D。
【分析】观察左图可知,阴影部分的面积=正方形的面积-空白圆的面积,后面几个图形的空白部分都可以转化成一个与左图大空白圆相等的面积,所以它们的阴影部分的面积都与左图相等。
二、判断题
4.【答案】 错误
【解析】【解答】解:周长和面积的意义不同,是不可能相等的。原题说法错误。
故答案为:错误。
【分析】半径为4厘米的圆的周长和面积的数字都是12.56,但是周长的单位是厘米,面积的单位是平方厘米,表示的意义是不同的。
5.【答案】 错误
【解析】【解答】解:周长与面积不能比较大小。
故答案为:错误。
【分析】周长与面积单位不同,不能进行大小比较。
6.【答案】 错误
【解析】【解答】圆周率π为定值,故错误.
故答案为:错误.
【分析】圆周率与圆的大小无关,圆周率为定值,即可做出判断.
7.【答案】 正确
【解析】【解答】解:面积相等的两个圆,它们的周长也一定相等。
故答案为:正确。
【分析】圆的面积=πr2 , 所以当圆的面积相等时,那么它们的半径相等,圆的周长=2πr,所以它们的周长也一定相等。
三、填空题
8.【答案】3.14
【解析】【解答】2÷2=1(米);
3.14×12
=3.14×1
=3.14(平方米).
故答案为:3.14 .
【分析】已知圆的直径,要求圆的面积,先求出圆的半径,圆的半径=直径÷2,然后用公式:S=πr2 , 据此求出圆的面积即可.
9.【答案】 20.56;25.12
【解析】【解答】半圆的周长:
3.14×4+2×4
=12.56+8
=20.56(厘米)
半圆的面积:
3.14×42÷2
=3.14×16÷2
=50.24÷2
=25.12(平方厘米)
故答案为:20.56;25.12。
【分析】已知一个半圆的半径r,要求半圆的周长C半圆 , 用公式:C半圆=πr+2r,要求半圆的面积S半圆 , 用公式:S半圆=πr2÷2,据此列式解答。
10.【答案】 25.12厘米;50.24平方厘米
【解析】【解答】解:周长:3.14×4×2=25.12(厘米),面积:3.14×42=50.24(平方厘米)。
故答案为:25.12厘米;50.24平方厘米。
【分析】圆规两脚间的距离是所画圆的半径;圆的周长=2πr;圆的面积=πr2。据此代入数据作答即可。
11.【答案】 (1)50.24
(2)16
(3)8
(4)25.12
(5)12.56
(6)4.56
(7)3.44
(8)157:200
【解析】【解答】(1)8÷2=4(厘米);
3.14×42
=3.14×16
=50.24(平方厘米);
(2)8÷2=4(厘米);
正方形AEHO的面积是:4×4=16(平方厘米);
(3)三角形区域①HGO的面积是:4×4÷2=8(平方厘米);
(4)半圆区域⑤的面积是;50.24÷2=25.12(平方厘米);
(5)扇形区域④的面积是:3.14×42×
=3.14×16×
=50.24×
=12.56(平方厘米);
(6)区域②的面积是:12.56-8=4.56(平方厘米);
(7)区域③的面积是:16-12.56=3.44(平方厘米);
(8)圆O与正方形ABCD的面积比是:50.24:(8×8)=50.24:64=0.785:1.
故答案为:(1)50.24;(2)16;(3)8;(4)25.12;(5)12.56;(6)4.56;(7)3.44;(8)157:200.
【分析】(1)观察图形可知,正方形的边长是圆的直径,先求出圆的半径,用直径÷2=半径,然后用公式:S=πr2 , 据此求出圆的面积;
(2)要求正方形AEHO的面积,先求出它的边长,观察图可知,它的边长是圆的半径,根据正方形的面积=边长×边长,据此列式解答;
(3)三角形区域①HGO是一个等腰直角三角形,底和高都是圆的半径,依据三角形的面积公式:底×高÷2=三角形面积 ,据此列式解答;
(4)半圆区域⑤的面积等于圆O的面积的一半,用圆O的面积÷2=半圆区域⑤的面积,据此列式解答;
(5)要求扇形区域④的面积,用扇形的面积公式:S=, 据此列式解答;
(6)要求区域②的面积,根据对称性可知,区域①和②的面积和等于区域④的面积,所以用区域④的面积-区域①的面积=区域②的面积,据此列式解答;
(7)要求区域③的面积,根据对称性,用正方形AEHO的面积-区域④的面积=区域③的面积,据此列式解答;
(8)要求圆O与正方形ABCD的面积比是多少,用圆O的面积:正方形的面积,然后化简成最简整数比即可.
12.【答案】 39.25
【解析】【解答】解:第四秒时,圆与正方形重叠部分是半圆,所以面积为3.14×52÷2=39.25(平方厘米)。
故答案为:39.25。
【分析】从图中可以看出,第四秒时,两个图形一共走的距离=(3+2)×4=20厘米,此时圆心恰好与正方形的左边的边重合,所以重叠部分是半圆,面积为3.14×52÷2=39.25(平方厘米)。
四、解答题
13.【答案】 解:35=5×7
20=2×2×5
所以20和35的最小公倍数是:2×2×5×7=140
即正方形的边长最小是140厘米
140×140=19600(平方厘米)
19600平方厘米=1.96平方米
则地砖的块数为:140×140÷(35×20)
=19600÷700
=28(块)
答:至少要28块砖,铺成的正方形的面积是1.96平方米。
【解析】【分析】用长方形的墙砖铺成正方形,则这个正方形的边长是这个长方形长和宽的最小公倍数,先用短除法或分解质因数法求出35和20的最小公倍数,这个最小公倍数就是正方形的边长。再根据正方形面积公式:S=a×a,求出正方形的面积,并转换单位为平方米;最后,用“正方形面积÷长方形墙砖的面积=所需墙砖数量”,求出需要多少块墙砖。
14.【答案】 解:3.14×(62.8÷3.14÷2)2×
=3.14×102×
=314×
=188.4(平方米)
答:种月季花的面积是188.4平方米。
【解析】【分析】种月季花的面积占总面积的。先根据圆周长公式用周长除以3.14再除以2求出半径,然后根据圆面积公式计算花坛面积,再根据分数乘法的意义用圆面积乘种月季花占总面积的f分率即可求出种月季花的面积。
五、应用题
15.【答案】周长: (米);
面积: (平方米).
答:圆的周长是31.4米,面积是78.5平方米。
【解析】【分析】已知圆的半径,求圆的周长,用公式:C=2πr,求圆的面积,用公式:S=πr2 , 据此列式解答.
16.【答案】 圆的面积=半径的平方×π , 所以面积之比和半径的平方成正比,两个圆的面积之比为4:9。
【解析】【解答】圆的面积=半径的平方×π , 所以面积之比和半径的平方成正比
【分析】考察了学生认识和辨别正比例和反比例的能力
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
