六年级上册数学一课一练-5.4身高的变化 北师大版(2014秋)(含答案)
文档属性
| 名称 | 六年级上册数学一课一练-5.4身高的变化 北师大版(2014秋)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 309.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 08:38:43 | ||
图片预览


文档简介
六年级上册数学一课一练-5.4身高的变化
一、单选题
1.折线统计图主要用来反映(??? )
A.?数量?????????????????????????????????????????B.?数量变化趋势
2.观察下边的折线统计图,哪一年实际产量超出计划产量最多( )。
A.?1999年????????????????????????????????????B.?2001年????????????????????????????????????C.?2002年
3.单式折线统计图和复式折线统计图的区别是(???? )
A.?单式折线统计图表示出数量的多少,复式折线统计图能反映出数据的变化情况。
B.?单式折线统计图比较简单,复式折线统计图不容易看懂。
C.?单式折线统计图只能表示出一组数据的增减变化情况,复式折线统计图能表示两组或两组以上的数据的增减变化情况。
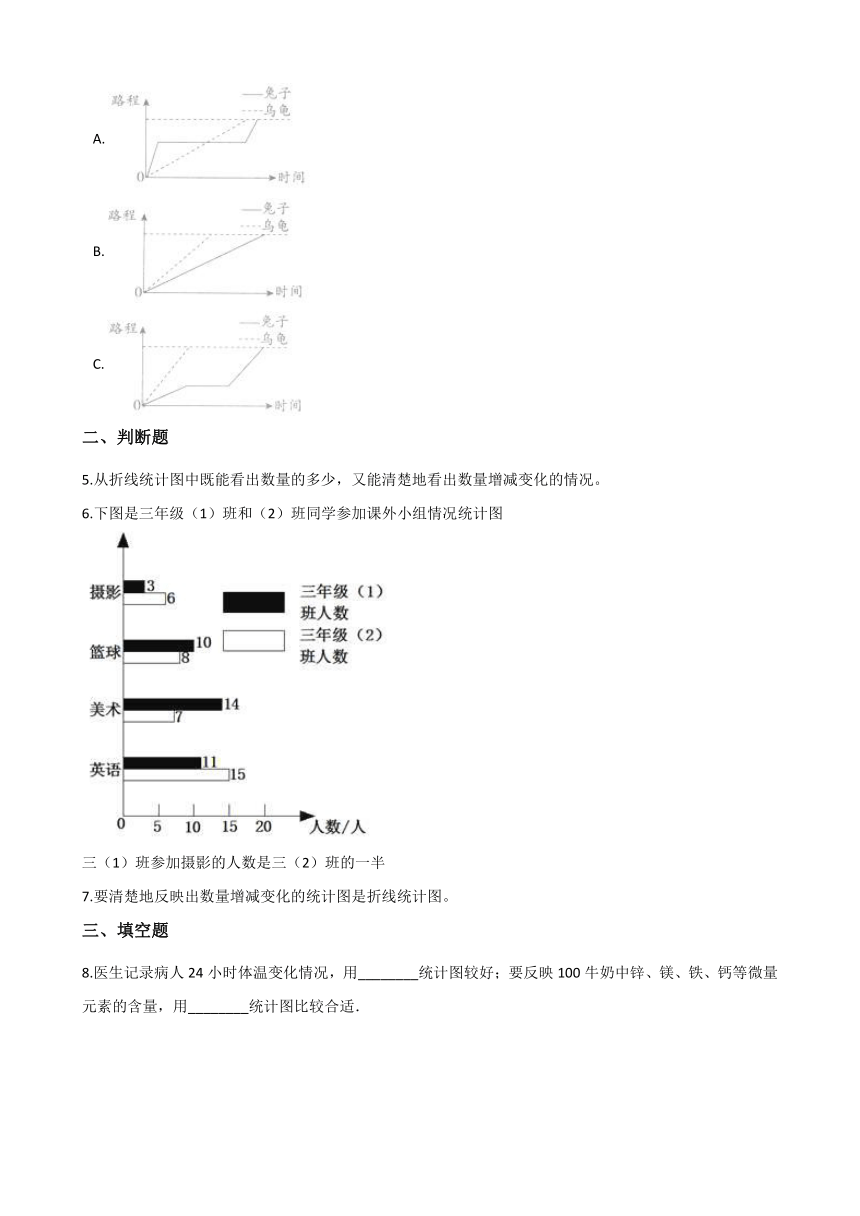
4.“龟兔赛跑”:领先的兔子看看慢慢爬行的乌龟,骄傲起来,睡了一觉。当它醒来时发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点。在下面三幅图所示的时间与路程关系中,最符合龟兔赛跑这则故事的是(??? )。
A.?
B.?
C.?
二、判断题
5.从折线统计图中既能看出数量的多少,又能清楚地看出数量增减变化的情况。
6.下图是三年级(1)班和(2)班同学参加课外小组情况统计图
三(1)班参加摄影的人数是三(2)班的一半
7.要清楚地反映出数量增减变化的统计图是折线统计图。
三、填空题
8.医生记录病人24小时体温变化情况,用________统计图较好;要反映100牛奶中锌、镁、铁、钙等微量元素的含量,用________统计图比较合适.
9.小李的年龄与身高的关系如下图。有一段时间,小李在2年内长高了15厘米,这两年小李的年龄最有可能在________岁至________岁之间。
10.根据统计图回答问题.已知六年级有男生110人,女生90人,平均每人捐款________元,六(3)班比六(4)班多捐款________%.
11.甲乙两公司近三年的利润如图所示,则________公司的效益较好。(填“甲”或“乙”)
四、解答题
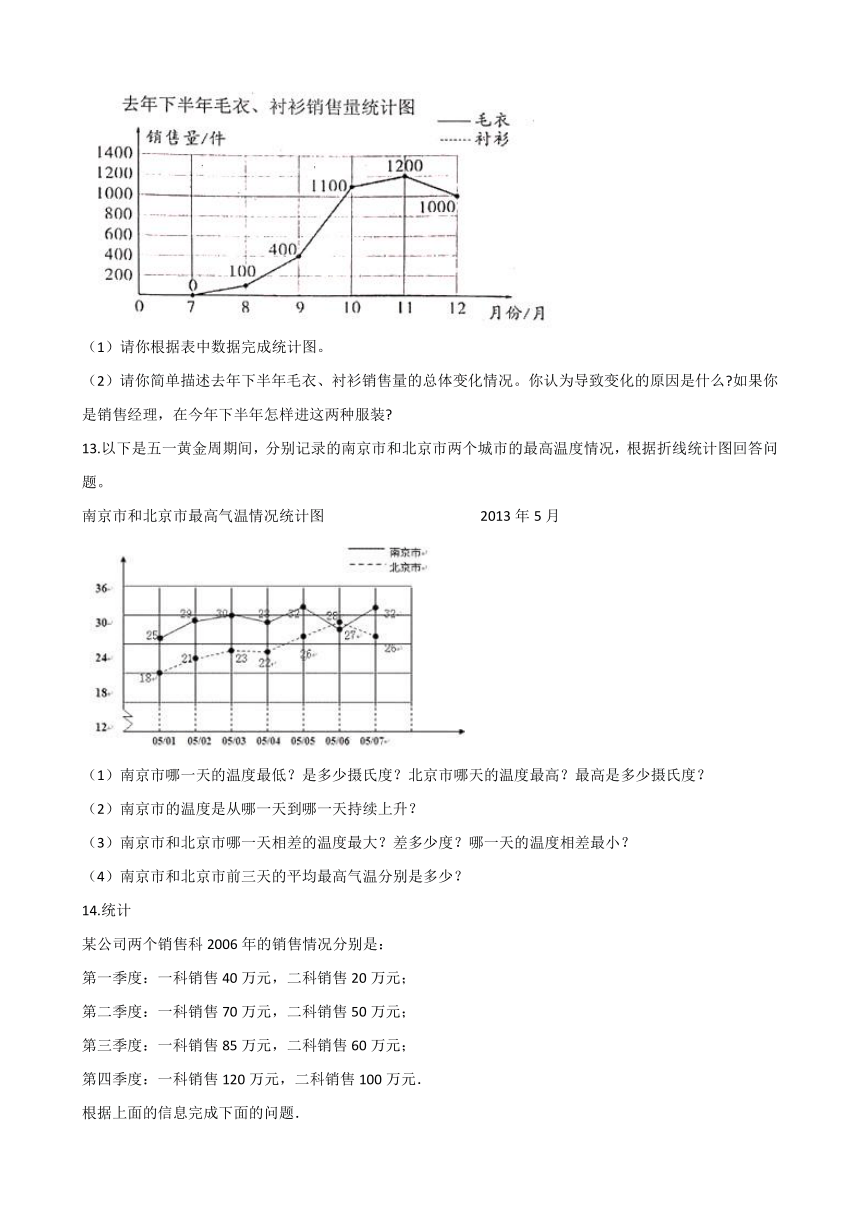
12.下面是去年下半年某商场毛衣和衬衫销售情况统计表和统计图。
(1)请你根据表中数据完成统计图。
(2)请你简单描述去年下半年毛衣、衬衫销售量的总体变化情况。你认为导致变化的原因是什么?如果你是销售经理,在今年下半年怎样进这两种服装?
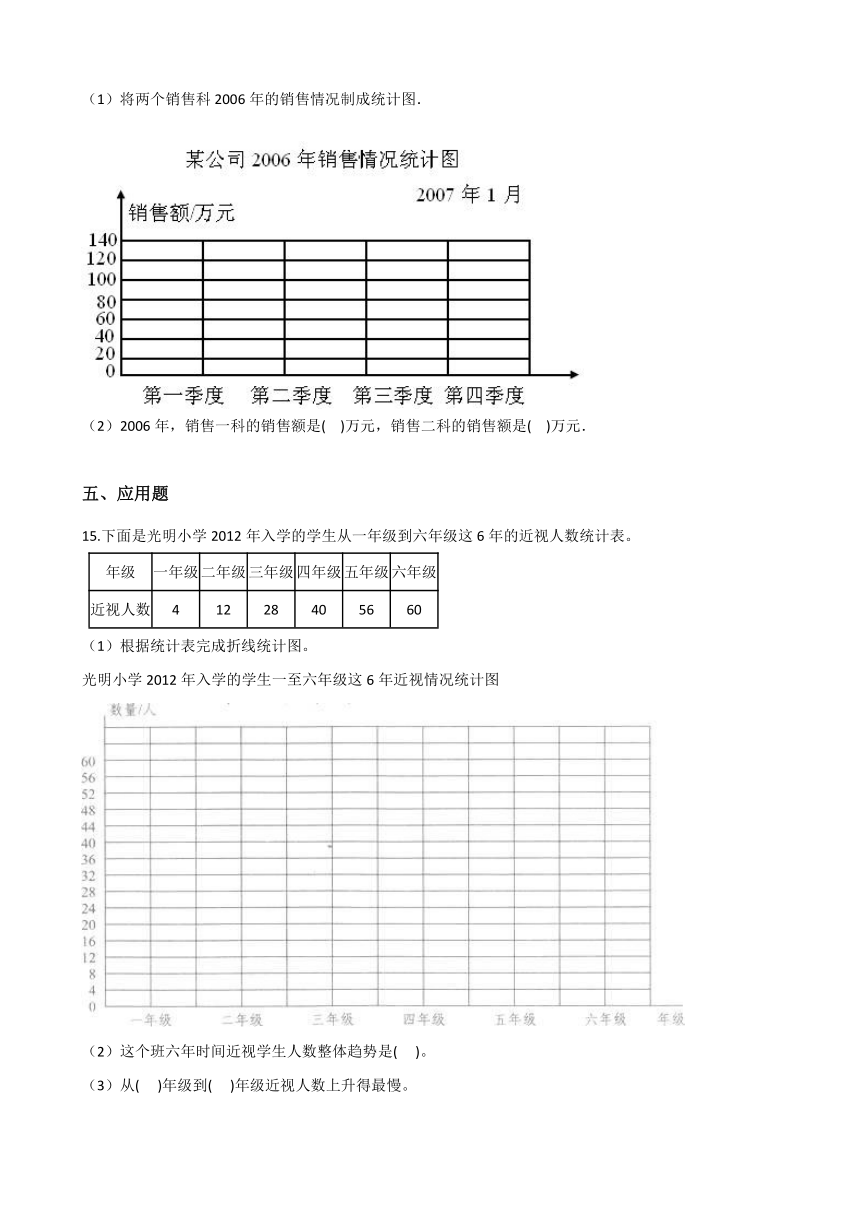
13.以下是五一黄金周期间,分别记录的南京市和北京市两个城市的最高温度情况,根据折线统计图回答问题。
南京市和北京市最高气温情况统计图 ????????????????????????????????????????? 2013年5月
(1)南京市哪一天的温度最低?是多少摄氏度?北京市哪天的温度最高?最高是多少摄氏度?
(2)南京市的温度是从哪一天到哪一天持续上升?
(3)南京市和北京市哪一天相差的温度最大?差多少度?哪一天的温度相差最小?
(4)南京市和北京市前三天的平均最高气温分别是多少?
14.统计
某公司两个销售科2006年的销售情况分别是:
第一季度:一科销售40万元,二科销售20万元;
第二季度:一科销售70万元,二科销售50万元;
第三季度:一科销售85万元,二科销售60万元;
第四季度:一科销售120万元,二科销售100万元.
根据上面的信息完成下面的问题.
(1)将两个销售科2006年的销售情况制成统计图.
(2)2006年,销售一科的销售额是( ??)万元,销售二科的销售额是( ??)万元.
五、应用题
15.下面是光明小学2012年入学的学生从一年级到六年级这6年的近视人数统计表。
年级
一年级
二年级
三年级
四年级
五年级
六年级
近视人数
4
12
28
40
56
60
(1)根据统计表完成折线统计图。
光明小学2012年入学的学生一至六年级这6年近视情况统计图
(2)这个班六年时间近视学生人数整体趋势是(??? )。
(3)从(??? )年级到(??? )年级近视人数上升得最慢。
参考答案
一、单选题
1.【答案】 B
【解析】【解答】折线统计图的主要作用是反映数量的变化趋势 【分析】考查了复式折线统计图的解决能力
2.【答案】 B
【解析】【解答】从图中可以看出,2001年对应的实际产量和计划产量相差最多,故选B
【分析】本题要求能读懂和会分析复式折线统计图中的数据
3.【答案】 C
【解析】【解答】解:根据折线统计图的特点可知:单式折线统计图只能表示出一组数据的增减变化情况,复式折线统计图能表示两组或两组以上的数据的增减变化情况.
故答案为:C
【分析】折线统计图是用折线表示数据的多少和数据的增减变化情况,由此根据折线统计图的特征判断单式和复式的区别即可.
4.【答案】 A
【解析】【解答】对于乌龟,其运动过程可分为两段:
从起点到终点乌龟没有停歇,其路程不断增加;
到终点后等待兔子这段时间路程不变,此时图象为水平线段.
对于兔子,其运动过程可分为三段:
开始跑得快,所以路程增加快;
中间睡觉时路程不变;
醒来时追赶乌龟路程增加快.
分析图象可知,选项A正确。
故选:A。
【分析】因为领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达终点,所以兔子的路程随时间的变化分为3个阶段,由此即可求出答案。
二、判断题
5.【答案】 正确
【解析】【解答】解:从折线统计图中既能看出数量的多少,又能清楚地看出数量增减变化情况。原题说法正确。
故答案为:正确。
【分析】折线统计图中各点的数据可以看出数量的多少,用折线的走势判断数量的增减变化情况。
6.【答案】 正确
【解析】【解答】一班摄影的长度是二班的一半
【分析】考察了复式条形统计图的解决能力
7.【答案】 正确
【解析】【解答】要反映数量的增减变化情况,可以选用折线统计图。
【分析】对折线统计图的理解
三、填空题
8.【答案】折线;扇形
【解析】【解答】解:医生记录病人24小时体温变化情况,用折线统计图较好;要反映100牛奶中锌、镁、铁、钙等微量元素的含量,用扇形统计图比较合适。
故答案为:折线,扇形。
【分析】本题直接根据各种统计图的特征进行解答即可。
9.【答案】0;5
【解析】【解答】解:根据统计图中的数据可知,这两年小李的年龄最有可能在0岁至5岁之间.
故答案为:0;5
【分析】0~5岁的身高差是61厘米,另外的身高差分别是23厘米,33厘米,5厘米,3厘米;这些数据都是5年长的高度,2年内长高了15厘米,生长速度比较快,因此应该是在0至5岁之间.
10.【答案】4.25;40
【解析】【解答】解:(150+100+350+250)÷(110+90)
=850÷200
=4.25(元)
(350-250)÷250
=100÷250
=40%
故答案为:4.25;40
【分析】根据统计图中的数据,把每班捐款的钱数相加,再除以六年级的总人数即可求出平均每人捐款的钱数;用3班与4班的钱数差除以4班的钱数即可求出多捐的百分率.
11.【答案】乙
【解析】【解答】甲公司2006年的利润是40,2008年是60,乙公司2006年的利润是30,2008年达到70多,通过比较发现乙公司的效益更好。
【分析】考查根据这线统计图提供的信息,解决有关的实际问题,关键是把两幅统计图进行比较,正确分析。
四、解答题
12.【答案】 (1)
(2)毛衣销售量从7月到11月呈逐渐上升趋势,12月份略有下降;衬衫销售量从7月到12月呈逐渐下降趋势;原因是天气情况,天气越冷,毛衣销售量越大,衬衫销售量越小,天气越热,毛衣销售量越小,衬衫销售量越大;如果我是销售经理,在今年下半年,我少进一些衬衫,多进一些毛衣。
【解析】【分析】(1)观察统计图可知,纵轴每格代表销售200件衣服,横格代表销售月份,根据统计表中的数据绘制复式折线统计图即可;
(2)观察复式折线统计图可知,毛衣销售量从7月到11月呈逐渐上升趋势,12月份略有下降;衬衫销售量从7月到12月呈逐渐下降趋势;原因是天气情况,天气越冷,毛衣销售量越大,衬衫销售量越小,天气越热,毛衣销售量越小,衬衫销售量越大;如果我是销售经理,在今年下半年,我少进一些衬衫,多进一些毛衣。
13.【答案】 (1)解:5月5日南京市温度最高,是32摄氏度;北京市5月6日温度最高,是28摄氏度.
(2)解:从5月1日到5月3日南京市的最高温度持续上升.
(3)解:30-23=7℃,5月2日两城市温度相差最大,差7摄氏度;5月6日相差最小.
(4)解:南京市:
(25+29+30)÷3
=84÷3
=28(摄氏度)
北京市:(18+21+23)÷3
=62÷3
≈20.7(摄氏度)
答:南京市前三天的平均气温是28摄氏度,北京市前三天的平均气温是20.7摄氏度.
【解析】【分析】(1)根据各点对应的温度判断最高温度和最低温度即可;(2)根据折线的走势判断南京市温度持续上升的天数;(3)根据对应点的数据判断温差最大和最小的天数;(4)用前三天的温度和除以3,分别计算两个城市前三天的平均温度即可.
14.【答案】 (1)解:制作折线统计图如下:
(2)解:40+70+85+120=315(万元);20+50+60+100=230(万元)
所以,2006年,销售一科的销售额是315万元,销售二科的销售额是230万元.
【解析】【分析】(1)一科用实线表示,二科用虚线表示,根据统计数据先描出各点,再依次连线即可;(2)把每科的销售额相加即可.
五、应用题
15.【答案】 (1)解:如图:
(2)解:这个班六年时间近视学生人数整体趋势是上升。
(3)解:从五年级到六年级近视人数上升得最慢。
【解析】【分析】(1)横轴表示年级,竖轴表示人数,一格表示4人,根据统计表中的数据先找出对应的点,然后把这些点顺次连接绘制成折线统计图;
(2)根据折线的走势判断近视人数的趋势;
(3)根据折线上升的程度结合数据判断上升最慢的阶段即可。
一、单选题
1.折线统计图主要用来反映(??? )
A.?数量?????????????????????????????????????????B.?数量变化趋势
2.观察下边的折线统计图,哪一年实际产量超出计划产量最多( )。
A.?1999年????????????????????????????????????B.?2001年????????????????????????????????????C.?2002年
3.单式折线统计图和复式折线统计图的区别是(???? )
A.?单式折线统计图表示出数量的多少,复式折线统计图能反映出数据的变化情况。
B.?单式折线统计图比较简单,复式折线统计图不容易看懂。
C.?单式折线统计图只能表示出一组数据的增减变化情况,复式折线统计图能表示两组或两组以上的数据的增减变化情况。
4.“龟兔赛跑”:领先的兔子看看慢慢爬行的乌龟,骄傲起来,睡了一觉。当它醒来时发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达了终点。在下面三幅图所示的时间与路程关系中,最符合龟兔赛跑这则故事的是(??? )。
A.?
B.?
C.?
二、判断题
5.从折线统计图中既能看出数量的多少,又能清楚地看出数量增减变化的情况。
6.下图是三年级(1)班和(2)班同学参加课外小组情况统计图
三(1)班参加摄影的人数是三(2)班的一半
7.要清楚地反映出数量增减变化的统计图是折线统计图。
三、填空题
8.医生记录病人24小时体温变化情况,用________统计图较好;要反映100牛奶中锌、镁、铁、钙等微量元素的含量,用________统计图比较合适.
9.小李的年龄与身高的关系如下图。有一段时间,小李在2年内长高了15厘米,这两年小李的年龄最有可能在________岁至________岁之间。
10.根据统计图回答问题.已知六年级有男生110人,女生90人,平均每人捐款________元,六(3)班比六(4)班多捐款________%.
11.甲乙两公司近三年的利润如图所示,则________公司的效益较好。(填“甲”或“乙”)
四、解答题
12.下面是去年下半年某商场毛衣和衬衫销售情况统计表和统计图。
(1)请你根据表中数据完成统计图。
(2)请你简单描述去年下半年毛衣、衬衫销售量的总体变化情况。你认为导致变化的原因是什么?如果你是销售经理,在今年下半年怎样进这两种服装?
13.以下是五一黄金周期间,分别记录的南京市和北京市两个城市的最高温度情况,根据折线统计图回答问题。
南京市和北京市最高气温情况统计图 ????????????????????????????????????????? 2013年5月
(1)南京市哪一天的温度最低?是多少摄氏度?北京市哪天的温度最高?最高是多少摄氏度?
(2)南京市的温度是从哪一天到哪一天持续上升?
(3)南京市和北京市哪一天相差的温度最大?差多少度?哪一天的温度相差最小?
(4)南京市和北京市前三天的平均最高气温分别是多少?
14.统计
某公司两个销售科2006年的销售情况分别是:
第一季度:一科销售40万元,二科销售20万元;
第二季度:一科销售70万元,二科销售50万元;
第三季度:一科销售85万元,二科销售60万元;
第四季度:一科销售120万元,二科销售100万元.
根据上面的信息完成下面的问题.
(1)将两个销售科2006年的销售情况制成统计图.
(2)2006年,销售一科的销售额是( ??)万元,销售二科的销售额是( ??)万元.
五、应用题
15.下面是光明小学2012年入学的学生从一年级到六年级这6年的近视人数统计表。
年级
一年级
二年级
三年级
四年级
五年级
六年级
近视人数
4
12
28
40
56
60
(1)根据统计表完成折线统计图。
光明小学2012年入学的学生一至六年级这6年近视情况统计图
(2)这个班六年时间近视学生人数整体趋势是(??? )。
(3)从(??? )年级到(??? )年级近视人数上升得最慢。
参考答案
一、单选题
1.【答案】 B
【解析】【解答】折线统计图的主要作用是反映数量的变化趋势 【分析】考查了复式折线统计图的解决能力
2.【答案】 B
【解析】【解答】从图中可以看出,2001年对应的实际产量和计划产量相差最多,故选B
【分析】本题要求能读懂和会分析复式折线统计图中的数据
3.【答案】 C
【解析】【解答】解:根据折线统计图的特点可知:单式折线统计图只能表示出一组数据的增减变化情况,复式折线统计图能表示两组或两组以上的数据的增减变化情况.
故答案为:C
【分析】折线统计图是用折线表示数据的多少和数据的增减变化情况,由此根据折线统计图的特征判断单式和复式的区别即可.
4.【答案】 A
【解析】【解答】对于乌龟,其运动过程可分为两段:
从起点到终点乌龟没有停歇,其路程不断增加;
到终点后等待兔子这段时间路程不变,此时图象为水平线段.
对于兔子,其运动过程可分为三段:
开始跑得快,所以路程增加快;
中间睡觉时路程不变;
醒来时追赶乌龟路程增加快.
分析图象可知,选项A正确。
故选:A。
【分析】因为领先的兔子看着缓慢爬行的乌龟,骄傲起来,睡了一觉,当它醒来时,发现乌龟快到终点了,于是急忙追赶,但为时已晚,乌龟还是先到达终点,所以兔子的路程随时间的变化分为3个阶段,由此即可求出答案。
二、判断题
5.【答案】 正确
【解析】【解答】解:从折线统计图中既能看出数量的多少,又能清楚地看出数量增减变化情况。原题说法正确。
故答案为:正确。
【分析】折线统计图中各点的数据可以看出数量的多少,用折线的走势判断数量的增减变化情况。
6.【答案】 正确
【解析】【解答】一班摄影的长度是二班的一半
【分析】考察了复式条形统计图的解决能力
7.【答案】 正确
【解析】【解答】要反映数量的增减变化情况,可以选用折线统计图。
【分析】对折线统计图的理解
三、填空题
8.【答案】折线;扇形
【解析】【解答】解:医生记录病人24小时体温变化情况,用折线统计图较好;要反映100牛奶中锌、镁、铁、钙等微量元素的含量,用扇形统计图比较合适。
故答案为:折线,扇形。
【分析】本题直接根据各种统计图的特征进行解答即可。
9.【答案】0;5
【解析】【解答】解:根据统计图中的数据可知,这两年小李的年龄最有可能在0岁至5岁之间.
故答案为:0;5
【分析】0~5岁的身高差是61厘米,另外的身高差分别是23厘米,33厘米,5厘米,3厘米;这些数据都是5年长的高度,2年内长高了15厘米,生长速度比较快,因此应该是在0至5岁之间.
10.【答案】4.25;40
【解析】【解答】解:(150+100+350+250)÷(110+90)
=850÷200
=4.25(元)
(350-250)÷250
=100÷250
=40%
故答案为:4.25;40
【分析】根据统计图中的数据,把每班捐款的钱数相加,再除以六年级的总人数即可求出平均每人捐款的钱数;用3班与4班的钱数差除以4班的钱数即可求出多捐的百分率.
11.【答案】乙
【解析】【解答】甲公司2006年的利润是40,2008年是60,乙公司2006年的利润是30,2008年达到70多,通过比较发现乙公司的效益更好。
【分析】考查根据这线统计图提供的信息,解决有关的实际问题,关键是把两幅统计图进行比较,正确分析。
四、解答题
12.【答案】 (1)
(2)毛衣销售量从7月到11月呈逐渐上升趋势,12月份略有下降;衬衫销售量从7月到12月呈逐渐下降趋势;原因是天气情况,天气越冷,毛衣销售量越大,衬衫销售量越小,天气越热,毛衣销售量越小,衬衫销售量越大;如果我是销售经理,在今年下半年,我少进一些衬衫,多进一些毛衣。
【解析】【分析】(1)观察统计图可知,纵轴每格代表销售200件衣服,横格代表销售月份,根据统计表中的数据绘制复式折线统计图即可;
(2)观察复式折线统计图可知,毛衣销售量从7月到11月呈逐渐上升趋势,12月份略有下降;衬衫销售量从7月到12月呈逐渐下降趋势;原因是天气情况,天气越冷,毛衣销售量越大,衬衫销售量越小,天气越热,毛衣销售量越小,衬衫销售量越大;如果我是销售经理,在今年下半年,我少进一些衬衫,多进一些毛衣。
13.【答案】 (1)解:5月5日南京市温度最高,是32摄氏度;北京市5月6日温度最高,是28摄氏度.
(2)解:从5月1日到5月3日南京市的最高温度持续上升.
(3)解:30-23=7℃,5月2日两城市温度相差最大,差7摄氏度;5月6日相差最小.
(4)解:南京市:
(25+29+30)÷3
=84÷3
=28(摄氏度)
北京市:(18+21+23)÷3
=62÷3
≈20.7(摄氏度)
答:南京市前三天的平均气温是28摄氏度,北京市前三天的平均气温是20.7摄氏度.
【解析】【分析】(1)根据各点对应的温度判断最高温度和最低温度即可;(2)根据折线的走势判断南京市温度持续上升的天数;(3)根据对应点的数据判断温差最大和最小的天数;(4)用前三天的温度和除以3,分别计算两个城市前三天的平均温度即可.
14.【答案】 (1)解:制作折线统计图如下:
(2)解:40+70+85+120=315(万元);20+50+60+100=230(万元)
所以,2006年,销售一科的销售额是315万元,销售二科的销售额是230万元.
【解析】【分析】(1)一科用实线表示,二科用虚线表示,根据统计数据先描出各点,再依次连线即可;(2)把每科的销售额相加即可.
五、应用题
15.【答案】 (1)解:如图:
(2)解:这个班六年时间近视学生人数整体趋势是上升。
(3)解:从五年级到六年级近视人数上升得最慢。
【解析】【分析】(1)横轴表示年级,竖轴表示人数,一格表示4人,根据统计表中的数据先找出对应的点,然后把这些点顺次连接绘制成折线统计图;
(2)根据折线的走势判断近视人数的趋势;
(3)根据折线上升的程度结合数据判断上升最慢的阶段即可。
同课章节目录
- 一 圆
- 1 圆的认识(一)
- 2 圆的认识(二)
- 3 欣赏与设计
- 4 圆的周长
- 5 圆的面积(一)
- 6 圆的面积(二)
- 二 分数的混合运算
- 1 分数的混合运算(一)
- 2 分数的混合运算(二)
- 3 分数的混合运算(三)
- 三 观察物体
- 1 搭积木比赛
- 2 观察的范围
- 3 天安门广场
- 四 百分数
- 1 百分数的认识
- 2 合格率
- 3 营养含量
- 4 这月我当家
- 五 数据处理
- 1 扇形统计图
- 2 统计图的选择
- 3 身高的情况
- 4 身高的变化
- 六 比的认识
- 1 生活中的比
- 2 比的化简
- 3 比的应用
- 数学好玩
- 1 反弹高度
- 2 看图找关系
- 3 比赛场次
- 七 百分数的应用
- 1 百分数的应用(一)
- 2 百分数的应用(二)
- 3 百分数的应用(三)
- 4 百分数的应用(四)
