人教版九年级数学下册 27.2 相似三角形的性质及应用学案(Word版 无答案)
文档属性
| 名称 | 人教版九年级数学下册 27.2 相似三角形的性质及应用学案(Word版 无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 361.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 08:47:54 | ||
图片预览




文档简介
相似三角形的性质及应用
要点一:
①相似三角形的周长之比等于相似比
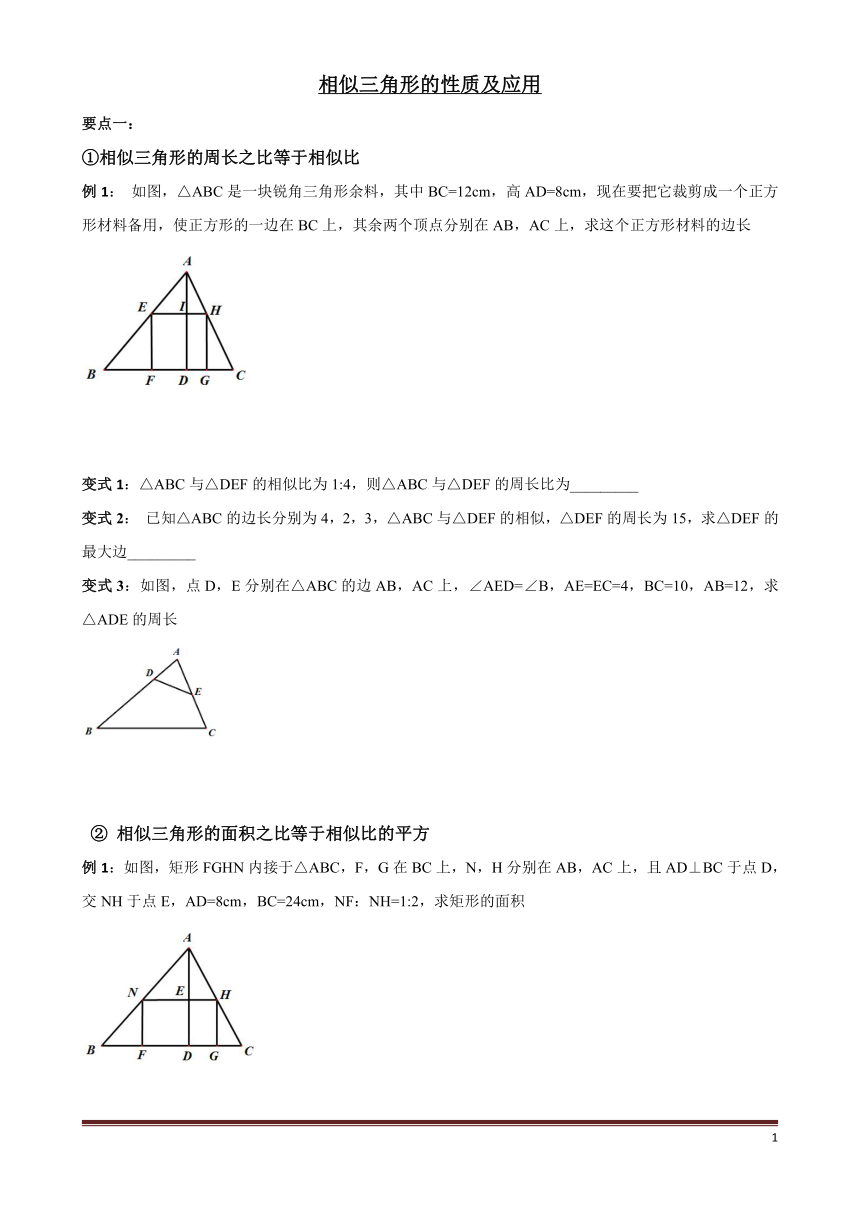
例1:
如图,△ABC是一块锐角三角形余料,其中BC=12cm,高AD=8cm,现在要把它裁剪成一个正方形材料备用,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,求这个正方形材料的边长
变式1:△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为_________
变式2:
已知△ABC的边长分别为4,2,3,△ABC与△DEF的相似,△DEF的周长为15,求△DEF的最大边_________
变式3:如图,点D,E分别在△ABC的边AB,AC上,∠AED=∠B,AE=EC=4,BC=10,AB=12,求△ADE的周长
②
相似三角形的面积之比等于相似比的平方
例1:如图,矩形FGHN内接于△ABC,F,G在BC上,N,H分别在AB,AC上,且AD⊥BC于点D,交NH于点E,AD=8cm,BC=24cm,NF:NH=1:2,求矩形的面积
例2:如图,DE//BC,
=1,
=1
求:SABC
变式1:在△ABC中,D,E,F分别是边AB,BC,AC的中点,求△ABC与△DEF的面积比
变式2:
已知△ABC与△DEF的相似比为3:4,且两个三角形的面积之差为28,求△ABC的面积_________
变式3:已知△ABC与△DEF的相似比为2:1,且两个三角形的面积之和为60,求△ABC的面积_________
变式4:如图.在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为6,求△ABD的面积.
变式6:如图,BD是平行四边形ABCD的对角线,BE=EF=FD,则S△AMH:SABCD的值
变式7:如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,
CD=AB,点E、F分别为AB、AD的中点,求△AEF与多边形BCDFE的面积之比
变式8:如图,已知DE是△ABC的中位线,点M是DE的中点,CM的延长线交AB于点N,求S△DMN:SANME的值
③三角形对应边上的中线,高线,角平分线之比等于相似比
例1:如图,已知△ADE∽△ACB,AG是角平分线交DE于点F,交BC于点G,AF∶FG=3∶2,求DE∶BC.
变式1:如果△ABC∽△DEF,且AB=1
cm,它的对应边DE=3
cm,那么△ABC与△DEF的对应高的比是___________.
变式:2:如图,在△ABC中,D,E分别是AB,AC的中点,AM平分∠BAC交BC于点M,交DE于点N,则的值为( )
变式3:如图,已知△ABC∽△A′B′C′,AD,A′D′分别是角平分线,AE,A′E′分别是两三角形的高,求证:AD·A′E′=AE·A′D′.
④
三角形三条中线的交点叫三角形的重心,三角形的重心分每条中线成1:2的两条线段
例1:如图,在△ABC中,D是△ABC的重心,S△DEF=2,求△AEC的面积
变式1:已知在△ABC中,G是△ABC的重心,AG⊥CG,AG=3,CG=4,求BG的长
变式2:如图,点G是等边△ABC的重心,过点G作BC的平行线,分别交AB、AC于点D、E,点M在BC边上.如果以点B、D、M为顶点的三角形与以点C、E、M为顶点的三角形相似(但不全等),那么S△BDM:S△CEM的值
要点二:等积式或比例式的证明
例1、如图,△ABC中,AB=AC,射线BF交高AD于G,交AC于E,作CF//AB交BF于F.求证:.
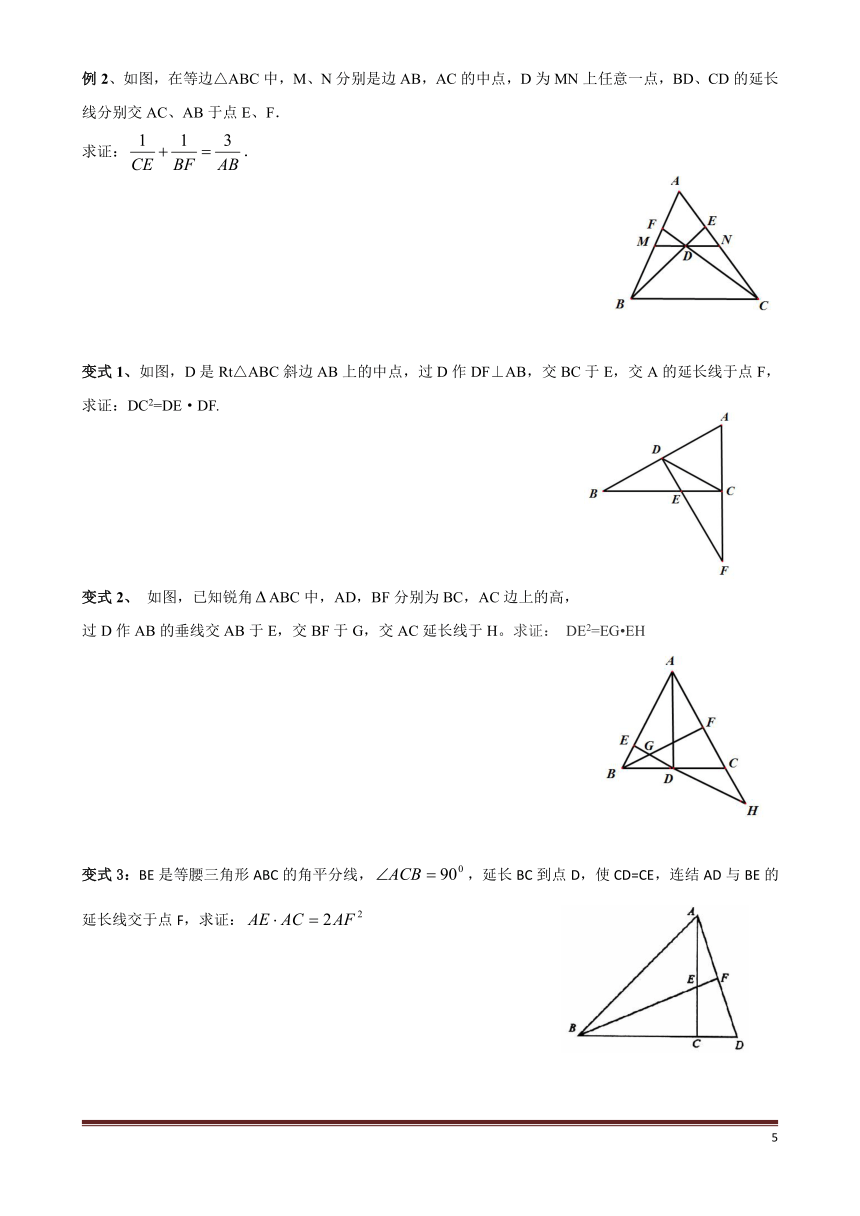
例2、如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点E、F.
求证:.
变式1、如图,D是Rt△ABC斜边AB上的中点,过D作DF⊥AB,交BC于E,交A的延长线于点F,求证:DC2=DE·DF.
变式2、
如图,已知锐角ABC中,AD,BF分别为BC,AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC延长线于H。求证:
DE2=EG?EH
变式3:BE是等腰三角形ABC的角平分线,,延长BC到点D,使CD=CE,连结AD与BE的延长线交于点F,求证:
变式4、已知:如图,梯形ABCD中,AB//DC,对角线AC、BD交于O,过O作EF//AB分别交AD、BC于E、F。
求证:
要点三:相似三角形应用
例1:如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(
)
例2:晚上,小亮走在大街上,他发现:当他站在大街两边的两盏相同高度的路灯之间,并且自己被两边的路灯罩在地上的影子成一直线时,自己右边的影子长3米,左边影子长为1.5米,如图所示,已知自己身高为1.80米,两盏路灯之间相距12米,求路灯的高度。
例3:在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在
坡面上.已知铁塔底座宽CD=12m,塔影长DE=18m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为(
)
A.24m
B.22m
C.20m
D.18m=12m
例题4:
某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图,在
Rt△ABC中,∠C=90°,AC=30cm,AB=50cm,依次裁下宽为1cm的矩形纸条,若
使裁得的矩形纸条的长都不小于5cm,则每张彩纸能裁成的矩形纸条的总数
A.24
B.25
C.26
D.27
变式1:
如图,路灯距地面8m,身高1.6米的小明从距离路灯的底部(点O)20m的点A处,沿OA所在的直线行走14m到点B时,则人影的长度____________(填增加或减少多少)
变式2:如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是_________
米
变式3:如图,小明同学用自制三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=0.4m,EF=0.2cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
:变式4:
如图,在RtΔABC内有边长分别为]的三个正方形,则满足的关系式
A.
A.
A.
A.
变式5:
如图,一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm.现沿底边依次从下向上裁剪宽度均为3cm的矩形纸条.已知剪得的纸条中有一张是正方形,则这张纸条是第________张
变式6:
要点四:相似三角形综合题
例1:
点A,B分别在反比例函数,的图像上,且OA⊥OB,求的值
例2:、如图,已知四边形ABCD内接于直径为3的圆O,对角线AC是直径,对角线AC和BD的交点为P,AB=BD,且PC=0.6,求四边形ABCD的周长。
例题3:如图,已知A,B的坐标分别为(8,0:),(0,),C是AB的中点,过点C作轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为___.
变式1:如图,已知A在反比例函数在第一象限分支上的一点动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线,求的值
变式2:、如图,已知AD是△ABC外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.
(1)求证:FB=FC;
(2)求证:FB2=FA·FD;
(3)若AB是△ABC的外接圆的直径,∠EAC=120°,BC=6cm,求AD的长。
变式3:如图,已知P是⊙O直径AB延长线上的一点,直线PCD交⊙O于C、D两点,弦DF⊥AB于点H,CF交AB于点E;
(1)求证:PA·PB=PO·PE;
(2)若DE⊥CF,∠P=15°,⊙O的半径为2,求弦CF的长。
变式4:已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),
,
(1)求过点A、B的直线的函数表达式;
(2)在轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P、Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似,如存在,请求出m的值;如不存在,请说明理由.
要点一:
①相似三角形的周长之比等于相似比
例1:
如图,△ABC是一块锐角三角形余料,其中BC=12cm,高AD=8cm,现在要把它裁剪成一个正方形材料备用,使正方形的一边在BC上,其余两个顶点分别在AB,AC上,求这个正方形材料的边长
变式1:△ABC与△DEF的相似比为1:4,则△ABC与△DEF的周长比为_________
变式2:
已知△ABC的边长分别为4,2,3,△ABC与△DEF的相似,△DEF的周长为15,求△DEF的最大边_________
变式3:如图,点D,E分别在△ABC的边AB,AC上,∠AED=∠B,AE=EC=4,BC=10,AB=12,求△ADE的周长
②
相似三角形的面积之比等于相似比的平方
例1:如图,矩形FGHN内接于△ABC,F,G在BC上,N,H分别在AB,AC上,且AD⊥BC于点D,交NH于点E,AD=8cm,BC=24cm,NF:NH=1:2,求矩形的面积
例2:如图,DE//BC,
=1,
=1
求:SABC
变式1:在△ABC中,D,E,F分别是边AB,BC,AC的中点,求△ABC与△DEF的面积比
变式2:
已知△ABC与△DEF的相似比为3:4,且两个三角形的面积之差为28,求△ABC的面积_________
变式3:已知△ABC与△DEF的相似比为2:1,且两个三角形的面积之和为60,求△ABC的面积_________
变式4:如图.在△ABC中,BC>AC,点D在BC上,且DC=AC,∠ACB的平分线CF交AD于点F,点E是AB的中点,连接EF.
(1)求证:EF∥BC;
(2)若四边形BDFE的面积为6,求△ABD的面积.
变式6:如图,BD是平行四边形ABCD的对角线,BE=EF=FD,则S△AMH:SABCD的值
变式7:如图,在四边形ABCD中,DC∥AB,CB⊥AB,AB=AD,
CD=AB,点E、F分别为AB、AD的中点,求△AEF与多边形BCDFE的面积之比
变式8:如图,已知DE是△ABC的中位线,点M是DE的中点,CM的延长线交AB于点N,求S△DMN:SANME的值
③三角形对应边上的中线,高线,角平分线之比等于相似比
例1:如图,已知△ADE∽△ACB,AG是角平分线交DE于点F,交BC于点G,AF∶FG=3∶2,求DE∶BC.
变式1:如果△ABC∽△DEF,且AB=1
cm,它的对应边DE=3
cm,那么△ABC与△DEF的对应高的比是___________.
变式:2:如图,在△ABC中,D,E分别是AB,AC的中点,AM平分∠BAC交BC于点M,交DE于点N,则的值为( )
变式3:如图,已知△ABC∽△A′B′C′,AD,A′D′分别是角平分线,AE,A′E′分别是两三角形的高,求证:AD·A′E′=AE·A′D′.
④
三角形三条中线的交点叫三角形的重心,三角形的重心分每条中线成1:2的两条线段
例1:如图,在△ABC中,D是△ABC的重心,S△DEF=2,求△AEC的面积
变式1:已知在△ABC中,G是△ABC的重心,AG⊥CG,AG=3,CG=4,求BG的长
变式2:如图,点G是等边△ABC的重心,过点G作BC的平行线,分别交AB、AC于点D、E,点M在BC边上.如果以点B、D、M为顶点的三角形与以点C、E、M为顶点的三角形相似(但不全等),那么S△BDM:S△CEM的值
要点二:等积式或比例式的证明
例1、如图,△ABC中,AB=AC,射线BF交高AD于G,交AC于E,作CF//AB交BF于F.求证:.
例2、如图,在等边△ABC中,M、N分别是边AB,AC的中点,D为MN上任意一点,BD、CD的延长线分别交AC、AB于点E、F.
求证:.
变式1、如图,D是Rt△ABC斜边AB上的中点,过D作DF⊥AB,交BC于E,交A的延长线于点F,求证:DC2=DE·DF.
变式2、
如图,已知锐角ABC中,AD,BF分别为BC,AC边上的高,过D作AB的垂线交AB于E,交BF于G,交AC延长线于H。求证:
DE2=EG?EH
变式3:BE是等腰三角形ABC的角平分线,,延长BC到点D,使CD=CE,连结AD与BE的延长线交于点F,求证:
变式4、已知:如图,梯形ABCD中,AB//DC,对角线AC、BD交于O,过O作EF//AB分别交AD、BC于E、F。
求证:
要点三:相似三角形应用
例1:如图,△ABC中,∠A=78°,AB=4,AC=6.将△ABC沿图示中的虚线剪开,剪下的阴影三角形与原三角形不相似的是(
)
例2:晚上,小亮走在大街上,他发现:当他站在大街两边的两盏相同高度的路灯之间,并且自己被两边的路灯罩在地上的影子成一直线时,自己右边的影子长3米,左边影子长为1.5米,如图所示,已知自己身高为1.80米,两盏路灯之间相距12米,求路灯的高度。
例3:在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在
坡面上.已知铁塔底座宽CD=12m,塔影长DE=18m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为(
)
A.24m
B.22m
C.20m
D.18m=12m
例题4:
某班在布置新年联欢会会场时,需要将直角三角形彩纸裁成长度不等的矩形彩条,如图,在
Rt△ABC中,∠C=90°,AC=30cm,AB=50cm,依次裁下宽为1cm的矩形纸条,若
使裁得的矩形纸条的长都不小于5cm,则每张彩纸能裁成的矩形纸条的总数
A.24
B.25
C.26
D.27
变式1:
如图,路灯距地面8m,身高1.6米的小明从距离路灯的底部(点O)20m的点A处,沿OA所在的直线行走14m到点B时,则人影的长度____________(填增加或减少多少)
变式2:如图是一位同学设计的用手电筒来测量某古城墙高度的示意图.点P处放一水平的平面镜,光线从点A出发经平面镜反射后刚好到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,测得AB=2米,BP=3米,PD=12米,那么该古城墙的高度CD是_________
米
变式3:如图,小明同学用自制三角形纸板DEF测量树的高度AB,他调整自己的位置,设法使斜边DF保持水平,并且边DE与点B在同一直线上.已知纸板的两条直角边DE=0.4m,EF=0.2cm,测得边DF离地面的高度AC=1.5m,CD=8m,求树高AB.
:变式4:
如图,在RtΔABC内有边长分别为]的三个正方形,则满足的关系式
A.
A.
A.
A.
变式5:
如图,一张等腰三角形纸片,底边长15cm,底边上的高长22.5cm.现沿底边依次从下向上裁剪宽度均为3cm的矩形纸条.已知剪得的纸条中有一张是正方形,则这张纸条是第________张
变式6:
要点四:相似三角形综合题
例1:
点A,B分别在反比例函数,的图像上,且OA⊥OB,求的值
例2:、如图,已知四边形ABCD内接于直径为3的圆O,对角线AC是直径,对角线AC和BD的交点为P,AB=BD,且PC=0.6,求四边形ABCD的周长。
例题3:如图,已知A,B的坐标分别为(8,0:),(0,),C是AB的中点,过点C作轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为___.
变式1:如图,已知A在反比例函数在第一象限分支上的一点动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线,求的值
变式2:、如图,已知AD是△ABC外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连结FB,FC.
(1)求证:FB=FC;
(2)求证:FB2=FA·FD;
(3)若AB是△ABC的外接圆的直径,∠EAC=120°,BC=6cm,求AD的长。
变式3:如图,已知P是⊙O直径AB延长线上的一点,直线PCD交⊙O于C、D两点,弦DF⊥AB于点H,CF交AB于点E;
(1)求证:PA·PB=PO·PE;
(2)若DE⊥CF,∠P=15°,⊙O的半径为2,求弦CF的长。
变式4:已知:如图,在平面直角坐标系中,△ABC是直角三角形,∠ACB=90°,点A、C的坐标分别为A(-3,0),C(1,0),
,
(1)求过点A、B的直线的函数表达式;
(2)在轴上找一点D,连接DB,使得△ADB与△ABC相似(不包括全等),并求点D的坐标;
(3)在(2)的条件下,如P、Q分别是AB和AD上的动点,连接PQ,设AP=DQ=m,问是否存在这样的m使得△APQ与△ADB相似,如存在,请求出m的值;如不存在,请说明理由.
