人教版五年级上册解方程例2(共20张ppt)
文档属性
| 名称 | 人教版五年级上册解方程例2(共20张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 326.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-23 00:00:00 | ||
图片预览







文档简介
解方程
例2
1、什么叫方程的解?
一、复习:
使方程左右两边相等的未知数的值,叫做
方程的解。
求方程的解的过程叫做解方程。
2、什么叫解方程?
X+15= 48 X-3.2=2.6
(1)你解这四个方程的依据和方法。
(2)说出等式的另外一个基本性质。
注意“不为0”
解答后说一说
2、解方程
6.5+ x=80.5 x-5=4.25
一、复习:
二、合作探究
1、阅读教材68页主题图,理解图意。
探究3x=18的解法
方法分析。
根据等式的性质(二),在方程两边同时( )3即可。刚好把左边变成1个( )。把例2中的解题过程补充完整。
3x=18
解:3x÷( )=18÷( )
X=6
二、合作探究
2、在方程的两边同时( )一个不为0的数,( )两边仍然相等。
3、讨论解方程需要注意什么?
二、合作探究
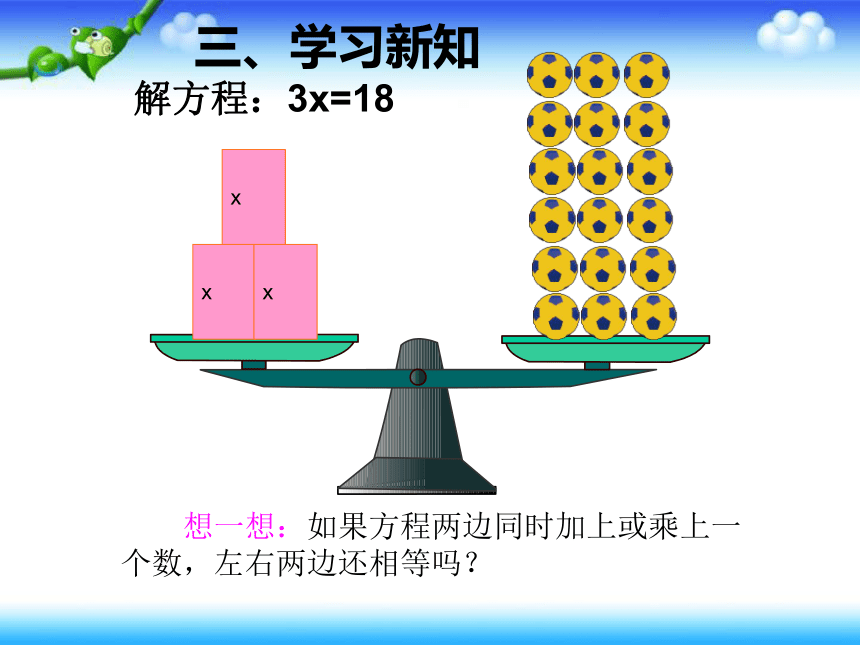
解方程:3x=18
x
x
x
想一想:如果方程两边同时加上或乘上一个数,左右两边还相等吗?
三、学习新知
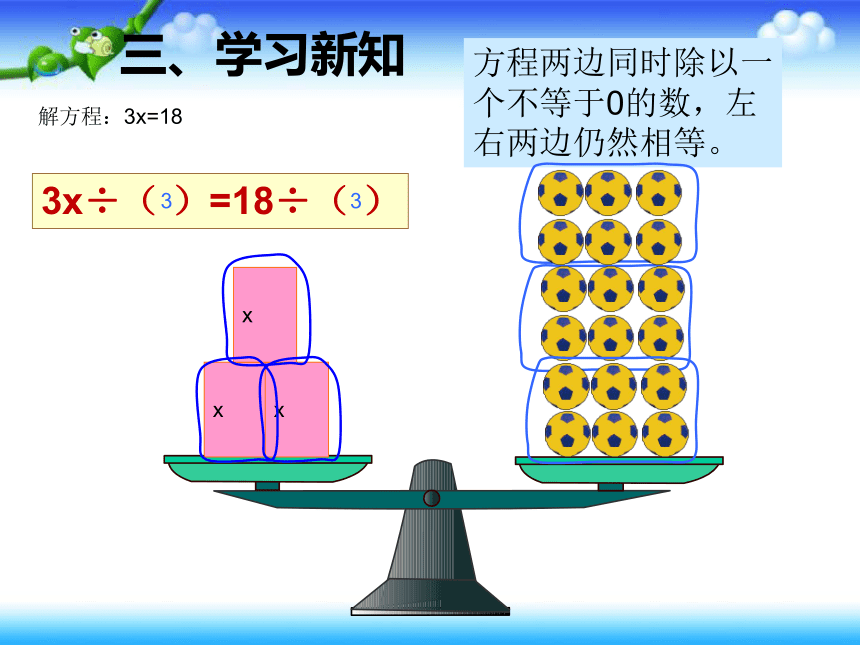
解方程:3x=18
方程两边同时除以一个不等于0的数,左右两边仍然相等。
x
x
x
3x÷( )=18÷( )
3
3
三、学习新知
解方程:3x=18
3x÷3=18÷3
x=6
解:
检验:方程左边=3x
=3?6
=18
=方程右边
所以 X=6是原方程的解.
小朋友,请注意格式哟
三、学习新知
解方程:X÷3=2.1
解: X÷3×3 =2.1×3
X=6.3
方程左边=X ÷3
=6.3 ÷3
=2.1
=方程右边
所以,X=6.3是方程的解。
三、学习新知
结合这道题的解题过程,谁能说说它的解题步骤和格式?
解方程的步骤及格式:
(1)先写“解:”。
(2)方程左右两边同时加或减一个相同的数,使方程左边只剩X,方程左右两边相等。(注意:“=”要对齐)
(3)求出X的值(注意:例如X=6 后面不带单位,因为它是一个数值。)
(4)验算。
三、学习新知
X元 X元 X元 X元
11.2元
4x=11.2
解: 4X÷4 =11.2÷4
X=2.8
四、当堂练习
1、根据题意写出等量关系,再列出方程。
(1)一本书有87页,小画看了x页,还剩34页没看.
数量关系式:
+ = 。
列方程:
四、当堂练习
1、根据题意写出等量关系,再列出方程。
(2)、把x粒糖平均分给4个小朋友,每人得5粒,刚好分完。平均每个小朋友分得多少粒?
数量关系式:
+ = 。
列方程:
四、当堂练习
1、根据题意写出等量关系,再列出方程。
(3)学校买了2箱乒乓球,每箱25元,共花了25元。每个乒乓球多少元,
数量关系式 :
+ = 。
列方程:
四、当堂练习
共128条
平均分在x个鱼缸里,每个鱼缸8条
128÷X=8
解:X=128÷8
X=16
除数=
被除数÷商
四、当堂练习
今天你有哪些收获?
1、懂得了什么是方程的解,学会了怎样解方程。
2、解方程时需要注意的 :
(1)、在解方程的开头写上“解:” 。
(2)、同时还要注意 “=” 对齐。
(3)、方程两边同时加减或乘除同一个(不为0)的数的过程要写出来。
1个排球和几个皮球重量相等?
=
等式两边都乘一个数(或除以一个不为0的数),等式仍然成立。
作业:完成书本第59页的做一做
例2
1、什么叫方程的解?
一、复习:
使方程左右两边相等的未知数的值,叫做
方程的解。
求方程的解的过程叫做解方程。
2、什么叫解方程?
X+15= 48 X-3.2=2.6
(1)你解这四个方程的依据和方法。
(2)说出等式的另外一个基本性质。
注意“不为0”
解答后说一说
2、解方程
6.5+ x=80.5 x-5=4.25
一、复习:
二、合作探究
1、阅读教材68页主题图,理解图意。
探究3x=18的解法
方法分析。
根据等式的性质(二),在方程两边同时( )3即可。刚好把左边变成1个( )。把例2中的解题过程补充完整。
3x=18
解:3x÷( )=18÷( )
X=6
二、合作探究
2、在方程的两边同时( )一个不为0的数,( )两边仍然相等。
3、讨论解方程需要注意什么?
二、合作探究
解方程:3x=18
x
x
x
想一想:如果方程两边同时加上或乘上一个数,左右两边还相等吗?
三、学习新知
解方程:3x=18
方程两边同时除以一个不等于0的数,左右两边仍然相等。
x
x
x
3x÷( )=18÷( )
3
3
三、学习新知
解方程:3x=18
3x÷3=18÷3
x=6
解:
检验:方程左边=3x
=3?6
=18
=方程右边
所以 X=6是原方程的解.
小朋友,请注意格式哟
三、学习新知
解方程:X÷3=2.1
解: X÷3×3 =2.1×3
X=6.3
方程左边=X ÷3
=6.3 ÷3
=2.1
=方程右边
所以,X=6.3是方程的解。
三、学习新知
结合这道题的解题过程,谁能说说它的解题步骤和格式?
解方程的步骤及格式:
(1)先写“解:”。
(2)方程左右两边同时加或减一个相同的数,使方程左边只剩X,方程左右两边相等。(注意:“=”要对齐)
(3)求出X的值(注意:例如X=6 后面不带单位,因为它是一个数值。)
(4)验算。
三、学习新知
X元 X元 X元 X元
11.2元
4x=11.2
解: 4X÷4 =11.2÷4
X=2.8
四、当堂练习
1、根据题意写出等量关系,再列出方程。
(1)一本书有87页,小画看了x页,还剩34页没看.
数量关系式:
+ = 。
列方程:
四、当堂练习
1、根据题意写出等量关系,再列出方程。
(2)、把x粒糖平均分给4个小朋友,每人得5粒,刚好分完。平均每个小朋友分得多少粒?
数量关系式:
+ = 。
列方程:
四、当堂练习
1、根据题意写出等量关系,再列出方程。
(3)学校买了2箱乒乓球,每箱25元,共花了25元。每个乒乓球多少元,
数量关系式 :
+ = 。
列方程:
四、当堂练习
共128条
平均分在x个鱼缸里,每个鱼缸8条
128÷X=8
解:X=128÷8
X=16
除数=
被除数÷商
四、当堂练习
今天你有哪些收获?
1、懂得了什么是方程的解,学会了怎样解方程。
2、解方程时需要注意的 :
(1)、在解方程的开头写上“解:” 。
(2)、同时还要注意 “=” 对齐。
(3)、方程两边同时加减或乘除同一个(不为0)的数的过程要写出来。
1个排球和几个皮球重量相等?
=
等式两边都乘一个数(或除以一个不为0的数),等式仍然成立。
作业:完成书本第59页的做一做
