人教版 八年级上册数学11.1 与三角形有关的线段提高复习讲义(2课时 无答案)
文档属性
| 名称 | 人教版 八年级上册数学11.1 与三角形有关的线段提高复习讲义(2课时 无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 09:01:26 | ||
图片预览



文档简介
【专题】
三角形培优复习
第一讲
三角形有关的线段
学生姓名:
学校:
时间:2小时
【学习目标】
1.三角形的表示方法及分类
2.三角形三边的关系
3.三角形的三条重要线段(高、中线、角平分线)
4.三角形的稳定性
【重点难点】
1.三角形三边的关系
2.三角形的稳定性
3.三角形的高、中线、角平分线
【知识点一】
三角形及其有关概念
1.三角形的表示
2.三角形的内角、外角
3.角的对边与边的对角
例题1
(1)如图1,在△ABC中,∠A的对边是
;在△ABD中,∠A的对边是
.
(2)如图2,以AD为边的三角形是
;以∠C为一个内角的三角
形是
;△AED的三个内角是
.
图1
图2
【知识点二】
三角形的分类
直角三角形
(1)按角分
斜三角形
三边都不相等的三角形
(2)按边分
等腰三角形
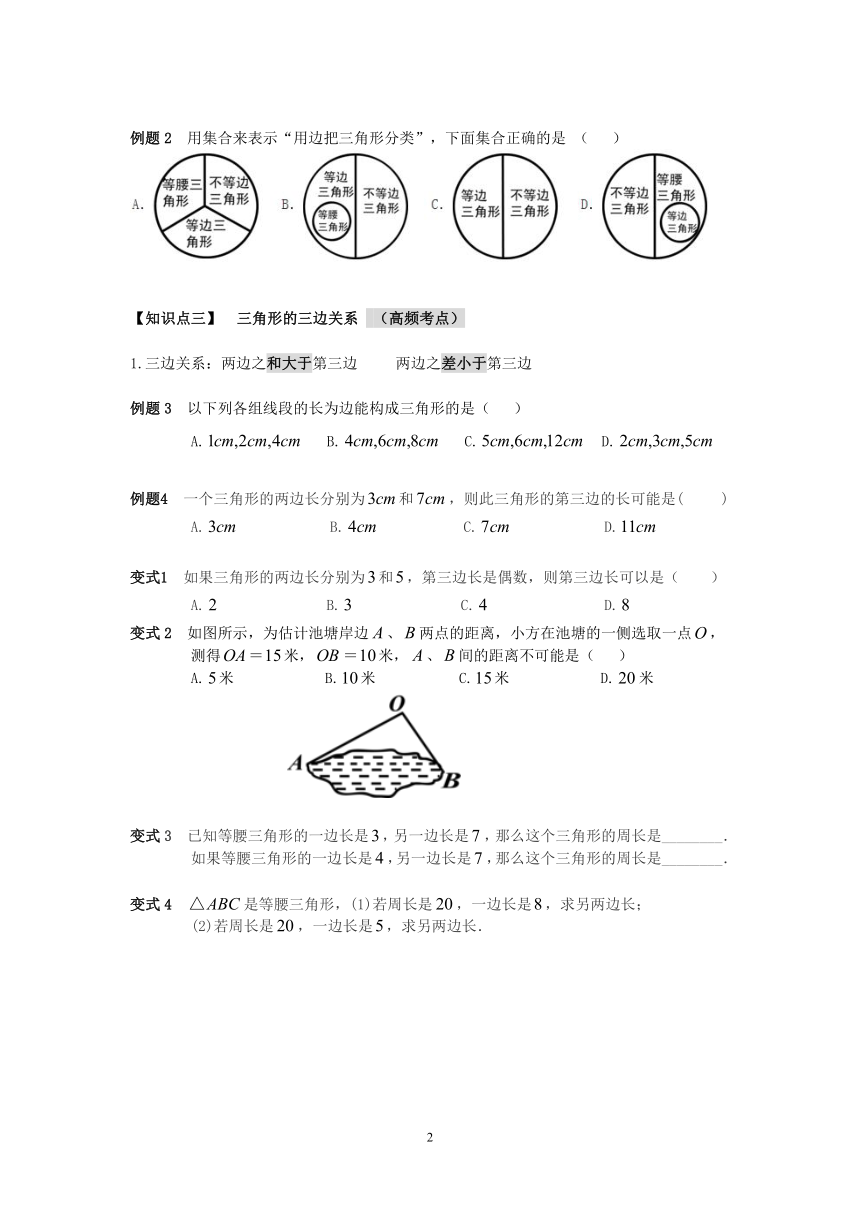
例题2
用集合来表示“用边把三角形分类”,下面集合正确的是
(
)
【知识点三】
三角形的三边关系
(高频考点)
1.三边关系:两边之和大于第三边
两边之差小于第三边
例题3
以下列各组线段的长为边能构成三角形的是(
)
A.
B.
C.
D.
例题4
一个三角形的两边长分别为和,则此三角形的第三边的长可能是(
)
A.
B.
C.
D.
变式1
如果三角形的两边长分别为和,第三边长是偶数,则第三边长可以是( )
A.
B.
C.
D.
变式2
如图所示,为估计池塘岸边、两点的距离,小方在池塘的一侧选取一点,测得=米,=米,、间的距离不可能是(
)
A.米
B.米
C.米
D.米
变式3
已知等腰三角形的一边长是,另一边长是,那么这个三角形的周长是________.
如果等腰三角形的一边长是,另一边长是,那么这个三角形的周长是________.
变式4
是等腰三角形,(1)若周长是,一边长是,求另两边长;
(2)若周长是,一边长是,求另两边长.
变式5
已知的三边长,,均为整数,且和满足
求中的边长.
【能力挑战】
1
已知一个三角形的两边长分别为,,且>,那么这个三角形的周长的取值范围是( )
A.
B.
C.
D.
2
若、、为△ABC三边,化简=________.
3
等腰三角形的周长为,则腰长的取值范围是________.
4
已知等腰三角形的三边长分别为,,,求三角形的周长.
5
在中,,边上的中线把三角形的周长分为和的两部分,求的长.
【知识点四】
三角形的高、中线、角平分线
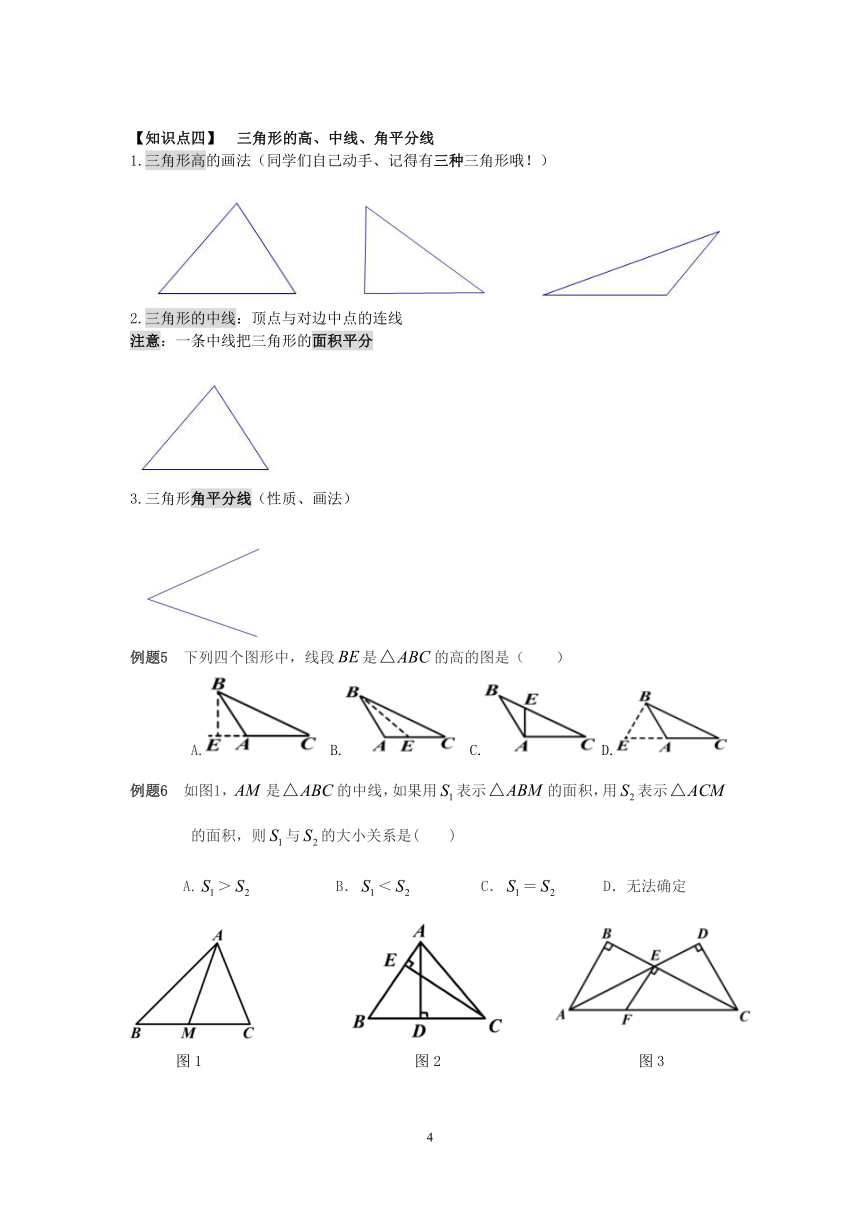
1.三角形高的画法(同学们自己动手、记得有三种三角形哦!)
2.三角形的中线:顶点与对边中点的连线
注意:一条中线把三角形的面积平分
3.三角形角平分线(性质、画法)
例题5
下列四个图形中,线段是的高的图是( )
A.
B.
C.
D.
例题6
如图1,是的中线,如果用表示的面积,用表示
的面积,则与的大小关系是( )
A.>
B.<
C.=
D.无法确定
图1
图2
图3
例题7
如图2,在中,、是的两条高,,,.则的长为
(
)
A.
B.
C.
D.
变式1
如图3,
(1)在中,边上的高是________;
(2)在中,边上的高是________;
(3)在中,边上的高是________;
(4)若,,则
=________.
变式2
如图所示,在中,、分别为、的中点,
且的面积为,则图形中阴影部分的面积是______.__
。
变式3
如图,在中,,是边上的高,,
,.求:(1)的面积;(2)的长.
【能力挑战】
1
如图,中,已知、、分别是、、的中点,且,则阴影部分面积为(
)
A.
B.
C.
D.
2
如图,有一块临河三角形河套土地,隔几年就被淹一次,老人去世后哥四个准备把地分开,老大老二要得到临河土地用来开沙场,老三老四怕被水淹要离河远一点的土地,如果你是村长,你能给这家分好土地吗?(要求土地分均匀)提出你的方案.
【知识点五】
三角形的稳定性
1.如图,木工师傅在做完门框后,为防止变形常常象图中所示那样钉上两条斜拉的木条(图中的,两根木条),这样做是运用了三角形的
【出门考】
1.已知等腰三角形的两边长分别为和,则它的周长为(
)
A.
B.
C.
D.或
2.如图
(?http:?/??/?www.tigu.cn?/?question_50443723.htm?)
(1),垂足为,则是______(填三角形)的高,________=________=;
(2)若平分,交于点,则叫______,
______=_______=______;
(3)若,则的中线是________,=________;
(4)若,则是________的中线,是________的中线.
3.已知,,分别是的三边长,,满足,且为方程
的解,求的周长,并判断的形状.
【课后作业】
1.小华在电话中问小明:“已知一个三角形三边长分别是,,,如何求这个三角形
的
面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形
正确的是(
)
A.
B.
C.
D.
2.如图,在中,已知点,分别为边,的中点,且,则等于________.
3.已知等腰三角形中,,为边上一点,且,的周长为,则底边的长为________.
4.若三角形的周长为,其中一边比最短边长,比最长边短,求三角形的三条边长.
【专题】
三角形培优复习
第二讲
三角形有关的角及多边形
【学习目标】
1.三角形的内角和
2.三角形的外角
3.多边形的内角和
4.多边形的外角和
【重点难点】
1.三角形的内角和
2.三角形的外角
【知识点一】
三角形内角和定理:
(高频考点)
证明过程:
例题1
等腰三角形中,一个角为,则这个等腰三角形的顶角的度数为( )
A.
B.
C.或
D.
例题2
已知三角形三个内角的度数之比为,求这三个内角的度数。
例题3
如图,在中,,,平分,则的度数是多少?
变式1
如图1所示,则的形状是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等腰三角形
图1
图2
变式2
已知:在中,比小,比大,则=________
=________,
=________
变式
3
如图2,的值为( )
A.
B.
C.
D.
变式4(新民)如图,已知为边延长线上一点,于交于,,,求的度数.
变式5
在中,,和的平分线相交于点.
求的度数.
【能力挑战】
1
如图所示,=_______
2
如图,把纸片沿折叠,当点落在四边形内部时,
?
(1)写出图中一对全等的三角形,并写出它们的所有对应角;?
(2)设的度数为,的度数为,那么,的度数分别是多少?(用含有或的代数式表示)?
(3)与之间有一种数量关系始终保持不变,请找出这个规律.
【知识点二】
三角形的外角及其性质
1.性质:三角形的一个外角等于与它不相邻的两个内角的和
例5
如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则=
.
【知识点三】
多边形的内角和
例6
八边形的内角和为(???
)
A.
??
??
B.
??
C.
?????
D.
变式1
一个多边形的内角和是,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
变式2
如图,在四边形中,若,则的度数为(??
)
A.
B.
C.
D.
变式3
已知:如图,五边形中,,,,求的度数.
知识点二、多边形的外角和
例7
如果一个正多边形的一个外角为,那么这个正多边形的边数是(
)
A.
B.
C.
D.
变式1
若一个多边形的外角和与它的内角和相等,则这个多边形是(
)边形.
A.三
B.四
C.五
D.六
变式2
多边形边数每增加一条,它的内角和会增加
,外角和增加
变式3
如图所示,已知,,,
则=
.
【出门考】
1.(新民)若等腰三角形的一角为,则它的底角是(
)。
A.
B.
C.
D.
2.(三美)某多边形的内角和是其外角和的倍,则此多边形的边数是(
)
A.
B.
C.
D.
3.(三美)等腰三角形一腰上的高与另一腰的夹角为,则等腰三角形的底角是(
)
A.
B.
C.
或
D.或
4.(十四中)如图,,的角平分线交于点,交于点.
(1)若,,求的度数;
(2)若,求的度数。
1
三角形培优复习
第一讲
三角形有关的线段
学生姓名:
学校:
时间:2小时
【学习目标】
1.三角形的表示方法及分类
2.三角形三边的关系
3.三角形的三条重要线段(高、中线、角平分线)
4.三角形的稳定性
【重点难点】
1.三角形三边的关系
2.三角形的稳定性
3.三角形的高、中线、角平分线
【知识点一】
三角形及其有关概念
1.三角形的表示
2.三角形的内角、外角
3.角的对边与边的对角
例题1
(1)如图1,在△ABC中,∠A的对边是
;在△ABD中,∠A的对边是
.
(2)如图2,以AD为边的三角形是
;以∠C为一个内角的三角
形是
;△AED的三个内角是
.
图1
图2
【知识点二】
三角形的分类
直角三角形
(1)按角分
斜三角形
三边都不相等的三角形
(2)按边分
等腰三角形
例题2
用集合来表示“用边把三角形分类”,下面集合正确的是
(
)
【知识点三】
三角形的三边关系
(高频考点)
1.三边关系:两边之和大于第三边
两边之差小于第三边
例题3
以下列各组线段的长为边能构成三角形的是(
)
A.
B.
C.
D.
例题4
一个三角形的两边长分别为和,则此三角形的第三边的长可能是(
)
A.
B.
C.
D.
变式1
如果三角形的两边长分别为和,第三边长是偶数,则第三边长可以是( )
A.
B.
C.
D.
变式2
如图所示,为估计池塘岸边、两点的距离,小方在池塘的一侧选取一点,测得=米,=米,、间的距离不可能是(
)
A.米
B.米
C.米
D.米
变式3
已知等腰三角形的一边长是,另一边长是,那么这个三角形的周长是________.
如果等腰三角形的一边长是,另一边长是,那么这个三角形的周长是________.
变式4
是等腰三角形,(1)若周长是,一边长是,求另两边长;
(2)若周长是,一边长是,求另两边长.
变式5
已知的三边长,,均为整数,且和满足
求中的边长.
【能力挑战】
1
已知一个三角形的两边长分别为,,且>,那么这个三角形的周长的取值范围是( )
A.
B.
C.
D.
2
若、、为△ABC三边,化简=________.
3
等腰三角形的周长为,则腰长的取值范围是________.
4
已知等腰三角形的三边长分别为,,,求三角形的周长.
5
在中,,边上的中线把三角形的周长分为和的两部分,求的长.
【知识点四】
三角形的高、中线、角平分线
1.三角形高的画法(同学们自己动手、记得有三种三角形哦!)
2.三角形的中线:顶点与对边中点的连线
注意:一条中线把三角形的面积平分
3.三角形角平分线(性质、画法)
例题5
下列四个图形中,线段是的高的图是( )
A.
B.
C.
D.
例题6
如图1,是的中线,如果用表示的面积,用表示
的面积,则与的大小关系是( )
A.>
B.<
C.=
D.无法确定
图1
图2
图3
例题7
如图2,在中,、是的两条高,,,.则的长为
(
)
A.
B.
C.
D.
变式1
如图3,
(1)在中,边上的高是________;
(2)在中,边上的高是________;
(3)在中,边上的高是________;
(4)若,,则
=________.
变式2
如图所示,在中,、分别为、的中点,
且的面积为,则图形中阴影部分的面积是______.__
。
变式3
如图,在中,,是边上的高,,
,.求:(1)的面积;(2)的长.
【能力挑战】
1
如图,中,已知、、分别是、、的中点,且,则阴影部分面积为(
)
A.
B.
C.
D.
2
如图,有一块临河三角形河套土地,隔几年就被淹一次,老人去世后哥四个准备把地分开,老大老二要得到临河土地用来开沙场,老三老四怕被水淹要离河远一点的土地,如果你是村长,你能给这家分好土地吗?(要求土地分均匀)提出你的方案.
【知识点五】
三角形的稳定性
1.如图,木工师傅在做完门框后,为防止变形常常象图中所示那样钉上两条斜拉的木条(图中的,两根木条),这样做是运用了三角形的
【出门考】
1.已知等腰三角形的两边长分别为和,则它的周长为(
)
A.
B.
C.
D.或
2.如图
(?http:?/??/?www.tigu.cn?/?question_50443723.htm?)
(1),垂足为,则是______(填三角形)的高,________=________=;
(2)若平分,交于点,则叫______,
______=_______=______;
(3)若,则的中线是________,=________;
(4)若,则是________的中线,是________的中线.
3.已知,,分别是的三边长,,满足,且为方程
的解,求的周长,并判断的形状.
【课后作业】
1.小华在电话中问小明:“已知一个三角形三边长分别是,,,如何求这个三角形
的
面积?”小明提示说:“可通过作最长边上的高来求解.”小华根据小明的提示作出的图形
正确的是(
)
A.
B.
C.
D.
2.如图,在中,已知点,分别为边,的中点,且,则等于________.
3.已知等腰三角形中,,为边上一点,且,的周长为,则底边的长为________.
4.若三角形的周长为,其中一边比最短边长,比最长边短,求三角形的三条边长.
【专题】
三角形培优复习
第二讲
三角形有关的角及多边形
【学习目标】
1.三角形的内角和
2.三角形的外角
3.多边形的内角和
4.多边形的外角和
【重点难点】
1.三角形的内角和
2.三角形的外角
【知识点一】
三角形内角和定理:
(高频考点)
证明过程:
例题1
等腰三角形中,一个角为,则这个等腰三角形的顶角的度数为( )
A.
B.
C.或
D.
例题2
已知三角形三个内角的度数之比为,求这三个内角的度数。
例题3
如图,在中,,,平分,则的度数是多少?
变式1
如图1所示,则的形状是( )
A.锐角三角形
B.钝角三角形
C.直角三角形
D.等腰三角形
图1
图2
变式2
已知:在中,比小,比大,则=________
=________,
=________
变式
3
如图2,的值为( )
A.
B.
C.
D.
变式4(新民)如图,已知为边延长线上一点,于交于,,,求的度数.
变式5
在中,,和的平分线相交于点.
求的度数.
【能力挑战】
1
如图所示,=_______
2
如图,把纸片沿折叠,当点落在四边形内部时,
?
(1)写出图中一对全等的三角形,并写出它们的所有对应角;?
(2)设的度数为,的度数为,那么,的度数分别是多少?(用含有或的代数式表示)?
(3)与之间有一种数量关系始终保持不变,请找出这个规律.
【知识点二】
三角形的外角及其性质
1.性质:三角形的一个外角等于与它不相邻的两个内角的和
例5
如图,一个直角三角形纸片,剪去直角后,得到一个四边形,则=
.
【知识点三】
多边形的内角和
例6
八边形的内角和为(???
)
A.
??
??
B.
??
C.
?????
D.
变式1
一个多边形的内角和是,则这个多边形是(
)
A.四边形
B.五边形
C.六边形
D.七边形
变式2
如图,在四边形中,若,则的度数为(??
)
A.
B.
C.
D.
变式3
已知:如图,五边形中,,,,求的度数.
知识点二、多边形的外角和
例7
如果一个正多边形的一个外角为,那么这个正多边形的边数是(
)
A.
B.
C.
D.
变式1
若一个多边形的外角和与它的内角和相等,则这个多边形是(
)边形.
A.三
B.四
C.五
D.六
变式2
多边形边数每增加一条,它的内角和会增加
,外角和增加
变式3
如图所示,已知,,,
则=
.
【出门考】
1.(新民)若等腰三角形的一角为,则它的底角是(
)。
A.
B.
C.
D.
2.(三美)某多边形的内角和是其外角和的倍,则此多边形的边数是(
)
A.
B.
C.
D.
3.(三美)等腰三角形一腰上的高与另一腰的夹角为,则等腰三角形的底角是(
)
A.
B.
C.
或
D.或
4.(十四中)如图,,的角平分线交于点,交于点.
(1)若,,求的度数;
(2)若,求的度数。
1
