沪教版数学九年级上-第5讲:期中练习学案-教师版
文档属性
| 名称 | 沪教版数学九年级上-第5讲:期中练习学案-教师版 |
|
|
| 格式 | docx | ||
| 文件大小 | 426.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 07:59:00 | ||
图片预览




文档简介
期中练习
内容分析
本讲整理了关于前两章相似三角形和锐角三角比的相关练习,以帮助同学们巩固所学.
知识结构
三角形一边的平行线
性质定理及推论
平行线分线段
成比例定理
比例线段
比例的性质
三角形一边的平行线
相
似形
判定定理及推论
相似三角形的概念
相似三角形
相似三角形的预备定理
相似三角形的判定定理
相似三角形的性质定理
运算法则
平行向量定理
实数与向量相乘
运算律
向量的线性组合
向量的线性运算
向量的分解
已知锐角,求三角比
锐角的三角比的概念
已知锐角的三角比,求锐角
已知一边和一个锐角
直角三角形中
的边角关系
解直角
三角形
已知两边
解直角
三角形的应用
选择题
【练习 1】已知在?ABC 中, ?C ? 90? , ?A ? ? ,AC = 3,那么 AB 的长为( )
A. 3sin? B. 3cos? C. 3
sin ?
D. 3 cos?
【难度】★
【答案】D
【解析】根据锐角三角比的概念,可得cos A ? AC ,即得: AB ?
AB
AC ?
cos A
3 .
cos?
【总结】本题主要考查锐角三角比的概念.
3
3
? 1 ?2
2
【练习 2】在?ABC 中,若? sin A ? ?
? ?
cot B ? ? 0 ,则?ABC 的形状是( )
A.等边三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
【难度】★
【答案】B
3
3
3
? 1 ?2 1
2
【解析】由? sin A ? ?
? ?
cot B ? ? 0 ,即可得sin A ? ,cot B ?
2
,由此可得?A ? 30? ,
3
?B ? 60? ,则?C ?180? ? ?A ? ?B ? 90? ,故选 B.
【总结】本题主要考查两非负数相加和为 0,则两个数均为 0 的知识点,结合特殊角的锐角三角比进行计算.
【练习 3】已知在?ABC 中, ?C ? 90? ,设 cos B = n,当?B 是最小的内角时,n 的取值范围是( )
A. 0 ? n ? 2
2
B. 0 ? n ? 1
2
C. 2 ? n ? 1
2
【难度】★
【答案】C
D. 1 ? n ? 1
2
【解析】?B 是最小内角,则0? ? ?B ? 45? ,根据余弦值的增减性, cos B ? cos 45? ? 2 ,
2
根据0 ? cos B ? 1,故选 C.
【总结】本题主要考查锐角三角比的增减性.
315350510114452817621011446059901101144【练习 4】如果向量a 与单位向量e 方向相反,且长度为 1 ,那么向量a 用单位向量e 表示
2
a ? 1 e
为( )
A.
2
B. a ? 2e
a ?? 1 e
5670367-30719C. D. a ? ?2e
2
2995589-299341【难度】★
【答案】C
304886297755【解析】方向相反,即可表示为a ? ?ne ?n ? 0?,长度为 1 ,可得n ? 1 ,故选 C.
2 2
【总结】考查平行向量的表示.
397346132490453840532490539341132490【练习 5】如图,在平行四边形 ABCD 中,如果 AB ? a , AD ? b ,那么 a ? b 等于( )
D
C
A
B
1665861-318832724818-318873791841-318834866258-31887A. BD B. AC C. DB D. CA
【难度】★
【答案】B
3686891-30781【解析】根据向量的“平行四边形法则”,得 AB ? AD ? AC .
【总结】考查向量运算的“平行四边形”法则.
【练习 6】下列不等式中正确的个数是( )
① sin 47? ? sin 48? ;② cos70? ? sin 30? ;③ tan 55? ? cot 55? ;④ cos 46? ? sin 46? ;
⑤ sin80? ? cot 42? .
A.1 个 B.2 个 C.3 个 D.4 个
【难度】★★
【答案】A
【解析】根据正弦值增减性,锐角正弦值随着角度增大而变大,①错误; cos70? ? sin 20? ,
②错误;锐角正切值随着角度增大而变大,cot 55? ? tan 35? ,③正确;cos46? ? sin 44? ,
④错误; cot 42? ? tan 48? ? tan 45? ?1, 0 ? sin80? ?1,⑤错误;③正确,故选 A.
【总结】考查锐角三角比的转化和相关增减性.
【练习 7】如图,已知 AD // BC,AC 与 BD 相交于点 O,点 G 是 BD 的中点,过点 G 作
GE // BC 交 AC 于点 E,如果 AD =1,BC = 3,那么 GE : BC 等于( )
A D
O
G E
B
C
A.1 : 2 B.1 : 3 C.1 : 4 D.2 : 3
【难度】★★
【答案】B
【解析】根据三角形一边平行线的性质定理,可得: DO ? AD ? 1 ,
BO BC 3
点G 是 BD 中点,可得: DO ? GO ,则有 AD ? DO ? 1,
GE GO
则有GE : BC ? AD : BC ?1: 3 .
【总结】考查三角形一边平行线性质定理的应用.
【练习 8】下列命题正确的个数有( )个
(1)长度相等的两个非零向量相等
(2)平行向量一定在同一直线上
(3)与零向量相等的向量必定是零向量
(4)任意两个相等的非零向量的始点与终点是一平行四边形的四个顶点
A.0 个 B.1 个 C.2 个 D.3 个
【难度】★★
【答案】B
【解析】相等的向量需确保方向相同,(1)错误;平行向量是同一平面内平行的两条有向线段,不一定在同一直线上,(2)错误;只有零向量模长为 0,可知与零向量相等的必定是零向量,(3)正确;相等向量可以在同一直线上,此时四个点不能构成四边形,
(4)错误.综上所述,只有(3)正确,故选 B.
【总结】考查与向量有关的相关定义的理解和把握.
3
3
3
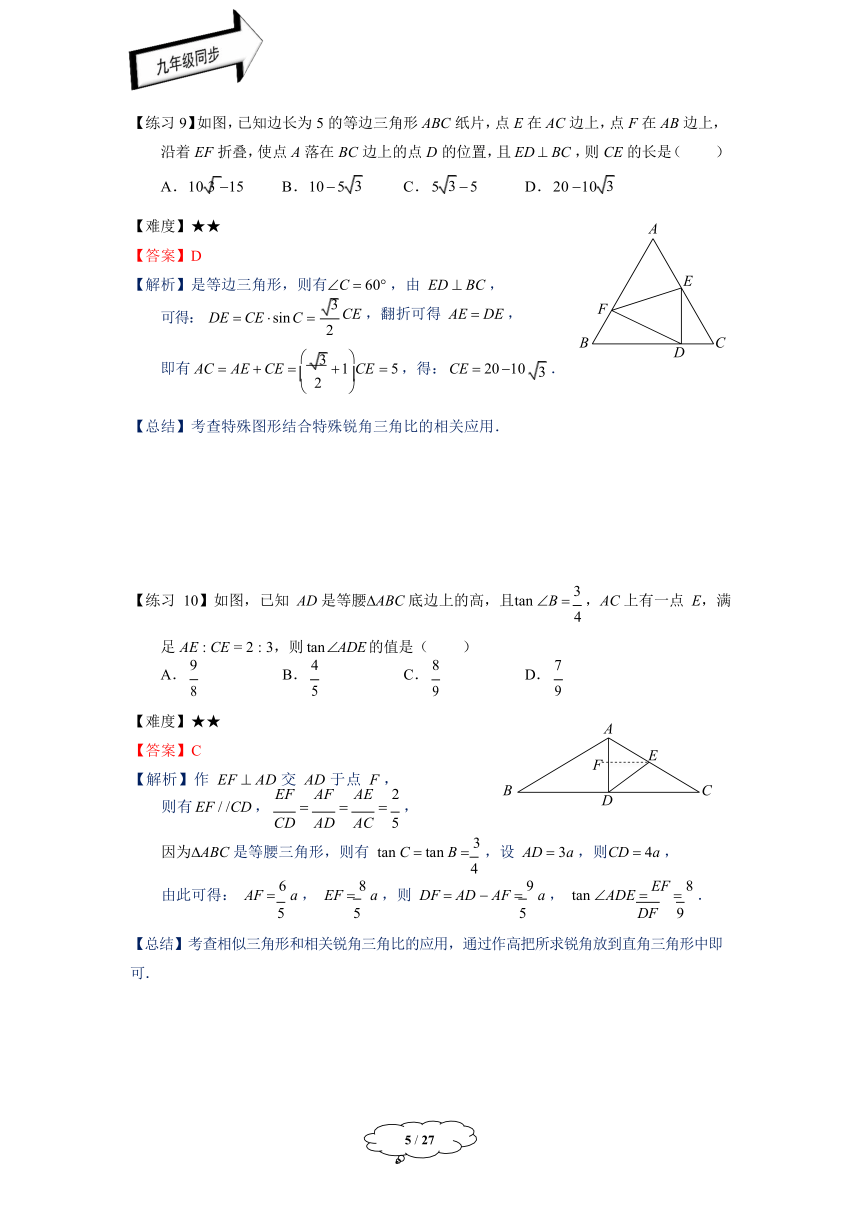
【练习 9】如图,已知边长为 5 的等边三角形 ABC 纸片,点 E 在 AC 边上,点 F 在 AB 边上, 沿着 EF 折叠,使点 A 落在 BC 边上的点 D 的位置,且 ED ? BC ,则 CE 的长是( )
178669346688A.10 3 ?15
B.10 ? 5
C. 5 ? 5
D. 20 ?10
A
E
F
B
D
C
【难度】★★
【答案】D
【解析】是等边三角形,则有?C ? 60? ,由 ED ? BC ,
可得: DE ? CE ? sin C ?
3 CE ,翻折可得 AE ? DE ,
2
27204651276203
? 3 ?
即有 AC ? AE ? CE ? ? ? 1?CE ? 5 ,得: CE ? 20 ?10 .
? 2 ?
【总结】考查特殊图形结合特殊锐角三角比的相关应用.
【练习 10】如图,已知 AD 是等腰?ABC 底边上的高,且tan ?B ? 3 ,AC 上有一点 E,满
4
足 AE : CE = 2 : 3,则 tan ?ADE 的值是( )
A. 9
8
【难度】★★
【答案】C
B. 4
5
C. 8
9
D. 7
9
B
A
F E D
C
【解析】作 EF ? AD 交 AD 于点 F ,
EF AF AE 2
则有 EF / /CD , ? ? ? ,
CD AD AC 5
因为?ABC 是等腰三角形,则有 tan C ? tan B ? 3 ,设 AD ? 3a ,则CD ? 4a ,
4
由此可得: AF ? 6 a , EF ? 8 a ,则 DF ? AD ? AF ? 9 a , tan ?ADE ? EF ? 8 .
5 5 5 DF 9
【总结】考查相似三角形和相关锐角三角比的应用,通过作高把所求锐角放到直角三角形中即可.
【练习 11】如图,D、E 分别是?ABC 的边 AB、AC 上的点,且 DE // BC,BE 交 DC 于点 F, EF : FB = 1 : 3,则 S?ADE : S?BCF 的值为( )
A.1 : 9 B.1 : 3 C.2 : 9 D.1 : 7
【难度】★★
A
D
E
F
B
C
【答案】C
【解析】由 DE // BC,即得:DE ? EF ? 1 ? AD ,则有 AD ? 1 ,
BC FB 3 AB DB 2
设 S ? a ,则 S
? 2a ,由 EF ? 1 ,即可得 S
? 1 a ,
?ADE
S ? EF ?2 1
?BDE
FB 3
9
?DEF 2
又 ?DEF ? ?
,即得: S? ? a .
? ?
FB
S?BCF ? ? 9
BCF 2
由此可得: S
?ADE
: S?BCF
? a : a
9
2
? 2 : 9 .
【总结】考查三角形一边平行线性质定理的应用,“A”字型和“8”字型的叠合应用,同时注意等高三角形面积和相似三角形面积比与相应边长的关系.
【练习 12】在一次夏令营活动中,小智从位于 A 点的营地出发,沿北偏东 60°方向走了 5 km
到达 B 地,然后再沿北偏西 30°方向走了若干千米到达 C 地,测得 A 地在 C 地南偏西
38546063728333
30°方向,则 A、C 两地的距离为( )km
A. 10 3
3
【难度】★★
【答案】A
B. 5 3
3
C. 5 2 D. 5
4854575-355264【解析】依题意可得到如图所示的图形,则有?BAE ? 60? ,
?2 ? ?3 ? 30? ,由 EF / /MN / /PQ ,可得: ?2 ? ?4 ? 30? ,
?1 ? ?BAE ? 60? ,则有?ABC ?180? ? ?1? ?2 ? 90? ,
?5 ? ?EAB ? ?CAE ? 30? ,则有?ACB ? 60? ,
由此可得: AB ? sin ?ACB ,又 AB ? 5 ,
AC
即得: AC ?
AB
sin 60?
? 10 3 km .
3
【总结】考查方位角知识的综合应用,结合特殊角的锐角三角比进行求解计算.
【练习 13】如图,小方同学在晚上由路灯 AC 走向路灯 BD,当他走到点 P 时,发现身后他影子的顶部刚好接触到路灯 AC 的底部,当他向前再步行 20 m 到达 Q 点时,发现身前他影子的顶部刚好接触到路灯 BD 的底部,已知小方的身高是 1.5 m,两个路灯的高度都是 9 m,则两路灯之间的距离是( )米
A.20 B.25 C.30 D.35
C
D
A P
Q B
【难度】★★
【答案】C
【解析】设 AP ? x ,依题意可得: BQ ? AP , 1.5 ? AP ,
BD AB
1.5 ?
x ,解得: x ? 5 ,则 AB ? 20 ? 2x ? 30 ,
9 2x ? 20
故选 C.
【总结】考查三角形一边平行线性质定理的实际应用.
【练习 14】如图,在 Rt?ABC 中, ?ABC ? 90? ,BA = BC,点 D 是 AB 的中点,连接 CD, 过点 B 作 BG ? CD ,分别交 CD、CA 于点 E、F,与过点 A 且垂直于 AB 的直线相交于点 G,连接 DF.给出以下四个结论:
AG ? FG ;(2)点 F 是 GE 的中点;(3) AF ?
AB FB
其中正确的个数有( )
2 AB ;(4) S
3
?ABC
? 5S
?BDF ,
A.1 个 B.2 个 C.3 个 D.4 个
C
G
F
E
A
D
B
【难度】★★★
【答案】B
【解析】由?BAG ? ?ABC ? 90? , ?ABG ? ?BCD , AB ? AC ,
可得: ?ABG ? ?BCD ,且有 AG / /BC ,则有 AG ? BD ? 1 BC ,
2
由此可得: AF ? GF ? AG ? 1 ,可知(1)正确;同时, CD 不
CF BF BC 2
是?ACB 的角平分线,可得 BE ? FE ,则 F 不是 GE 中点,
(2)错误;此时可得 AF ? 1 AC ? 2 AB ,(3)正确;则有 S
? 3S
? 6S ,
3 3
(4)错误;综上所述,正确的是(1)(3),故选 B.
?ABC
?ABF
?BDF
【总结】考查等腰直角三角形结合平行问题中特殊边角关系的综合应用.
【练习 15】如图,在正方形 ABCD 中,点 P 是 AB 上一动点(不与 A、B 重合),对角线 AC、
BD 相交于点 O,过点 P 分别作 AC、BD 的垂线,分别交 AC、BD 于点 E、F,交 AD、
BC 于点 M、N,下列结论:
(1)?APE ≌ ?AME ;(2)PM ? PN ? AC ;(3)PE2 ? PF 2 ? PO2 ;(4)?POF ∽ ?BNF ;
(5)当?PMN ∽ ?AMP 时,点 P 是 AB 的中点. 其中正确的结论有( )
A.5 个 B.4 个 C.3 个 D.2 个
【难度】★★★
M D
【答案】B
【解析】根据正方形的性质,即可得?PAE ? ?MAE ? 45? , E
P
由 PM ? AE , AE ? AE ,可得?APE ≌ ?AME ,(1)正确; O
36018961296924441621129692同理可得?PBF ? ?NBF ,则有 PM ? 2AP , PN ? 2PB , F
N C
237443434623325426134623则有 PM ? PN ? 2 ?PA ? PB? ? 2AB ? AC ,(2)正确;
由?AOB ? 90? ,可知四边形 PEOF 是矩形,则有 PE2 ? PF 2 ? PO2 ,(3)正确;?BNF
为等腰直角三角形, ?POF 是直角三角形,但不能确定为等腰,(4)错误; ?PMN ∽
318204366575365235866575?AMP 时,则有 PM ? PN ,即 2AP ? 2BP ,由此可得 AP ? BP ,P 为 AB 中点,(5)
正确;综上所述,正确的是(1)(2)(3)(5),故选 B.
【总结】本题综合性较强,主要考查正方形性质的综合应用,注意题目中由正方形得到的边角关系,从而利用勾股定理完成解题.
填空题
【练习 16】? 为锐角,(1)sin? ? 2 ,则 tan ? ?
3
;(2)cot? ? 3,则sin ? ? .
【难度】★
【答案】(1) 2 5 ;(2) 10 .
5 10
【解析】(1)由sin2 ? ? cos2 ? ? 1 ,可得: cos? ?
5 ,则tan? ? sin? ?
2 ? 2 5 ;
5
3 cos??5
(2)由cot ? ? cos? ? 3 ,可得cos? ? 3sin? ,又sin2 ? ? cos2 ? ? 1 ,即10sin2 ? ? 1 ,
sin ?
即得: sin? ?
10 .
10
【总结】考查锐角三角比之间的相互关系的转化,或利用设“ k ”法表示长度进行求解.
1106424-8717651? 2sin ? cos ? ?
【练习 17】? 为锐角,且cos? ? 1 ,则 .
2
【难度】★
【答案】 3 ? 1 .
2
【解析】? 为锐角, cos? ? 1 ,可得: ? ? 60? ,则sin? ?
2
3 ,由此即可化简得
2
1 ? 2sin? cos? ?
sin2 ? ? cos2 ? ? 2sin? cos? ? sin? ? cos? ?
3 ?1 .
2
【总结】考查sin2 ? ? cos2 ? ? 1 公式的灵活运用进行锐角三角比化简,也可利用特殊角的锐角三角比的值进行计算求值.
【练习 18】在正方形网格中, ?ABC 的位置如图所示,则cos ?B 的值为 .
【难度】★
C
B
A
【答案】 2 .
2
【解析】由图中所示格点位置,知?B ? 45? ,则cos ?B ? 2 .
2
【总结】考查利用格点三角形得到相关角的锐角三角比.
【练习 19】如图,在正方形网格上有 6 个三角形:① ?ABC ;② ?CDB ;③ ?DEB ;④ ?FBG ;
⑤ ?HGF ;⑥ ?EKF ,在②~⑥中,与①相似的三角形是 (填序号).
C
D
E
A
K
B
G
H
F
【难度】★
【答案】③④⑤
【解析】由图示可得: ?BAC ? 135? ,且有
2
AC ? ,满足条件的图形只有③⑤.同时
AB
利用三边对应成比例,也可证得④成立.
【总结】考查“格点三角形”中根据勾股定理得到特殊边角关系和长度的应用.
【练习 20】已知 P 是线段 AB 的一个黄金分割点,且 AB = 20 cm,AP < BP,那么 AP = .
【难度】★★
2128519105592【答案】?30 ?10 5 ?cm .
【解析】根据黄金分割点的意义,由 AP < BP,可得 BP ?
27832222144693798735214469AP ? AB ? BP ? 20 ? ?10 5 ?10?? ?30 ?10 5 ?cm .
5 ?1 AB ? 10 5 ?10 ,则有
5305453-1399572
【总结】考查线段的黄金分割点和相应的黄金比,注意线段的黄金分割点有两个.
【练习 21】如果从灯塔 A 处观察到船 B 在它的北偏东 35°方向上,那么从船 B 观察灯塔 A
的方向是 .
【难度】★★
【答案】南偏西35? .
【解析】换位观察,方向变为相反,偏离角度大小不变,即得.
【总结】考查方位角的基本性质.
【练习 22】如图, ?ABC 中,?C ? 90? ,sin A ? 3 ,D 为 AC 上一点,且 BD = AC,DC = 7
5
B
A
D
C
cm,则 AD = .
【难度】★★
7
【答案】?4 ? 7?cm .
【解析】设 BC ? acm ,由sin
A ? 3 ,可得:AB ? 5 a ,AC ? 4 a ,
5 3 3
根据勾股定理可得 BD ?
? a2 ? 49 ? AC ? 4 a ,
BC2 ? CD2
7
46877902560823
7
即可解得: a ? 3
,则 AC ? 4
, AD ? AC ? DC ? ?4 7 ? 7?cm .
【总结】考查共直角边的两个直角三角形结合锐角三角比的应用,根据题目条件进行边角转换即可.
【练习 23】传送带和地面所成斜坡的坡度为 1 : 0.75,它把物体从地面送到离地面高 8 米的地方,物体在传送带上所经过的路程为 米.
【难度】★★
【答案】10.
【解析】传送带和地面所成坡度i ? 1: 0.75 ,可知物体传送的水平距离即为 8 ? 6m ,根据勾
i
82 ? 62
股定理即可得物体在传送带经过路程为
? 10m .
【总结】考查坡度的意义和应用.
A
B
C
【练习 24】如图,在坡度为 1 : 2.5 的楼梯表面铺地毯,已知楼梯高度 AC = 2 米,则地毯长度至少是 .
【难度】★★
【答案】7m .
【解析】楼梯的坡度为 1 : 2.5,可得楼梯水平长度
BC ? AC ? 5m ,则地毯长度至少为 2 ? 5 ? 7m .
i
【总结】考查坡度意义的综合应用,注意地毯要沿着楼梯铺设,完全覆盖.
53495061836025861708183602【练习 25】如图,正方形 ABCD 中,M 是边 BC 上一点,且 BM ? 1 BC .若 AB ?a
4
,AD ? b ,
170671232037195221032037233192732042A
D
B
M
C
试用a , b 表示 DM ???.
【难度】★★
【答案】a ? 3 b .
4
1667608-306504246260-30650【解析】DM ? DC ? MC ,根据正方形的性质,可得:DC ? AB ? a ,
1435750167978BC ? AD ? b ,由 BM ? 1 BC ,可得: BM ? 1 BC ? 1 b ,则有
4 4 4
MC ? 3 b , DM ? a ? 3 b .
4 4
【总结】考查平面向量的线性运算,注意把握好相等向量的定义.
【练习 26】如图,点 G 是?ABC 的重心, AG ? GC ,AC = 4,那么 BG 的长为 .
A
G
D
B
C
【难度】★★
【答案】4
【解析】延长 BG 交 AC 于点 D ,则 D 是 AC 中点,
1
由 AG ? GC ,则有GD ?
即可得 BG ? 2GD ? 4 .
AC ? 2 ,根据重心性质,
2
【总结】本题主要考查重心性质的应用.
【练习 27】如图,在梯形 ABCD 中,AD // BC,BE 平分?ABC 交 CD 于 E,且 BE ? CD ,
CE : ED = 2 : 1,如果?BEC 的面积为 2,那么四边形 ABED 的面积是 .
【难度】★★
【答案】 7 .
4
D H
F E
【解析】作 AG / /DC 交 BC 于点G ,交 BE 于点 F ,
延长 BE 交 AD 延长线于点 H . B G C
由 AD // BC,得?DEH ∽ ?CEB , ?DEH ∽ ?AFH ,
S ? DE ?2 ? 1 ?2 1 1
则 有 ?DEH ? ? ?
?
,可得: S? ? .
CE 2
S?CEB
? ? ? ?
? ? ? ? 4
DEH 2
由 BE ? CD , AG / /CD ,得 AF ? BH ,又 BE 平分?ABC ,则有 AF ? FG ? 1 AG ,
2
1 1 2
S ? DE ?2 ? 2 ?2 4 9
即得:DE ?
CD ? AG ?
?
AF ,由此可得: ?DEH ? ? ?
???
,得 S? ? ,
AF 3
3 3 3
S?AFH
? ? ? ?
? ? ? ? 9
AFH 8
由 AD // BC,BE 平分?ABC ,可知?ABH 为等腰三角形,
则有 S四边形ABED
? 2S
?AFH
S?DEH
? 2 ? 9 ? 1 ? 7 .
8 2 4
【总结】考查根据平行构造相似三角形“A”字型和“8”字型的应用,相似三角形面积比即为相似比的平方,同时考查平行线与角平分线得到等腰三角形的基本图形.
【练习 28】某学校为新生设计的学生板凳的正面视图如图所示,其中 BA = CD,BC = 20 cm,
BC、EF 平行于地面 AD 且到地面 AD 的距离分别为 40 cm、8 cm.为使板凳两腿底端 A、
D 之间的距离为 50 cm,那么横梁 EF = .(材质及其厚度等暂忽略不计).
B
C
E
F
A
P
Q
D
N
M
【难度】★★
【答案】44cm .
【解析】如图,分别延长 BM、CN 交 AD 于点 P 和点 Q. 在等腰梯形中易得 AP ? DQ , EM ? FN ,
由 BC / /EF / / AD ,即得: BC ? MN ? PQ ? 20 ,则有
AP ? 15 ,题中 BM ? 40 ? 8 ? 32 , BP ? 40 ,由 EF / / AD ,则有 EM ? BM ,
AP BP
即 EM ? 32 ,得 EM ?12 ? FM ,则 EF ? EM ? MN ? NF ? 44cm .
15 40
【总结】考查三角形一边平行线性质定理的实际应用.
【练习 29】如图,在?ABC 中,?A ? ? ,?B ? ? ,AB = c,用? 、? 、c 表示 S?ABC ???.
C
A
D
B
【难度】★★
c2 tan? tan ?
【答案】
2?tan? ? tan ? ? .
【解析】作CD ? AB 交 AB 于点 D ,
则有 tan A ? CD , tan B ? CD ,
由此可得 AD ?
AD CD
tan?
, BD ?
BD
CD
tan ?
, AB ? AD ? BD ,
即 CD
tan?
1
CD
?
tan ?
? c ,可得: CD ? c tan? tan ? ,
tan? ? tan ?
c2 tan? tan ?
则 S?ABC ? 2 CD ? AB ? 2?tan? ? tan ? ? .
【总结】考查锐角三角比性质的综合应用,通过作高实现边角转换.
3437445135161【练习 30】在 Rt?ABC 中,斜边 AB ? 2 5 , 且 tan A ? tan B ? 5 ,
2
则 Rt?ABC 的面积是 .
【难度】★★
【答案】4.
【解析】设两直角边长分别为 a 、b ,根据锐角三角比的定义,tan A ? tan B ? 5 ,即
b ? a ? 5 ,
a2 ? b2 5
2 2 2
2 a b 2
1
? ,由勾股定理可得a ? b
ab 2
? AB
? 20 ,则有ab ? 8 , S?ABC ? 2 ab ? 4 .
【总结】考查锐角三角比的基本定义结合勾股定理的应用.
【练习 31】已知:如图,AD 是?ABC 的中线,E 为 AD 上的一点,且 AE ? 1 ,射线 CE 交
ED k
AB 于 F, AF
FB
【难度】★★
A
???.
F E
【答案】 1 . G
2k
【解析】作 DG / /EF 交 AB 于点G ,则有 AF ? AE ? 1 ,
FG ED k
因为 D 为 BC 中点,且 DG / /CF ,则G 为 BF 中点,
D C
即有 BF ? 2FG ,则 AF ?
FB
AF ? 1 .
2FG 2k
【总结】考查三角形一边平行线性质定理的应用,构造“A”“8”叠加的基本图形.
【练习 32】如图,在?ABC 中,AD 是 BC 上的高,且 BC = 5,AD = 3,矩形 EFGH 的顶点
F、G 在边 BC 上,顶点 E、H 分别在边 AB 和 AC 上,如果设边 EF 的长为 x(0 < x < 3),矩形 EFGH 的面积为 y,那么 y 关于 x 的函数解析式是 .
A
E
H
B
F
D G
C
【难度】★★
【答案】 y ? 5x ? 5 x2 .
3
【解析】由 EH / /BC ,EF / / AD ,根据三角形一边平行线的性质, 即得: EF ? BE , EH ? AE ,则有 EF ? EH ? 1 ,
AD AB
BC AB
AD BC
即 x ? EH ? 1 ,得: EH ? 5 ? 5 x , y ? EH ? EF ? 5x ? 5 x2 .
3 5 3 3
【总结】考查三角形一边平行线性质定理的综合应用,进行比例转化解决问题.
1106424-871952【练习 33】已知:在?ABC 中,AC = a,cos C = 4 ,AB 与 BC 所在直线成 45°角,则 AC 边
5
上的高的长是 . A
【难度】★★★
【答案】 21 a 或 3 a .
25 25
【解析】作 AD ? BC 所在直线于点 D ,
B C
D B'
由 AC = a,cos C = 4 ,可得CD ? 4 a ,勾股定理得 AD ? 3 a , AB 与 BC 所在直线成
5 5 5
45°角,由此需进行分类讨论,
B 在 D 点左侧,有?B ? 45? ,可得 BD ? AD ? 3 a ,则 BC ? CD ? BD ? 7 a ,
5
3 a ? 7 a
由面积法可得 AC 边上的高长为 AD ? BC ? 5 5
AC a
5
? 21 a ;
25
B ' 在 D 点右侧,有?B ' ? 45? ,可得 B ' D ? AD ? 3 a ,则 B 'C ? CD ? B ' D ? 1 a ,
5
3 a ? 1 a
由面积法可得 AC 边上的高长为 AD ? BC ? 5 5 ?
AC a
5
3 a .
25
【总结】考查多解性问题,由直线可知题目存在多解,结合锐角三角比和面积法即可求得高长,也可直接利用锐角三角比求高长.
【练习 34】如图所示,在?ABC 中,BC = 6,E、F 分别是 AB、AC 的中点,动点 P 在射线
EF 上,BP 交 CE 于 D, ?CBP 的平分线交 CE 于 Q, A
E P F
D
Q
C
当CQ ? 1 CE 时,EP + BP = .
3
G
【难度】★★★
【答案】12. B
【解析】延长 BQ 交 EF 延长线于点G .
由 E、F 分别是 AB、AC 中点,得 EF 为?ABC 中位线,
则有 EF / /BC ,可得: ?G ? ?GBC ,由?PBQ ? ?CBG ,则有?PBQ ? ?G ,
CE
则有 BP ? PG ,EP ? BP ? EG ,由CQ ? 1 ,则有CQ ? 1 EQ ,则有 BC ? CQ ? 1 ,
3 2
由 BC ? 6 ,则 EG ? 2BC ?12 ,即 EP ? BP ?12 .
EG EQ 2
【总结】考查角平分线与平行线产生等腰三角形的基本图形,构成“8”字型比例转换即可.
【练习 35】已知在?ABC 中, ?ACB ? 60? ,AC = 2,BC = 6,将?ABC 沿着 DE 翻折,使点 B 与点 C 重合,折痕 DE 交 AB 于点 D,交 BC 于点 E,那么?ACD 的面积为 .
A
D
【难度】★★★
【答案】 6 3 .
5
【解析】作 AF ? BC 交 BC 于点 F ,
3
由 AC ? 2 , ?ACB ? 60? ,可得: AF ? AC ? sin ?ACB ? ,C B F E
CF ? AC ? cos?ACB ?1 ,依题意可得 DE 垂直平分 BC ,则有 BE ? CE ? 1 BC ? 3 ,
2
DE ? BE ? 3 ,得: DE ? 3 3 , S
? S ? S
? 1 AF ? BC ? 1 DE ? BC ? 6 3 .
AF BF 5
5 ?ACD
?ABC
?BCD
2 2 5
【总结】考查特殊角的锐角三角比的应用和翻折性质的理解应用.
【练习 36】根据三角形外心的概念,我们可引入如下一个新定义:
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
根据准外心的定义,探究如下问题:如图,在 Rt?ABC 中,?A ? 90? ,BC = 10,AB = 6,
如果准外心 P 在边 AC 上,那么 PA 的长为 . C
【难度】★★★
【答案】4 或 7 .
4
BC2 ? AB2
P
【解析】根据勾股定理,可得: AC ?
? 8 .
1 A B
(1)点 P 到点 A 和点C 距离相等,则 P 为 AC 中点,此时则有 PA ?
AC ? 4 ;
2
(2)点 P 到点 B 和点C 距离相等,则有 PB ? PC ,设 PA ? x ,则 PC ? 8 ? x ? PB ,
在 Rt?ABP 中用勾股定理,则有 BP2 ? AB2 ? AP2 ,即?8 ? x?2 ? 62 ? x2 ,解得: x ? 7 .
4
故 AP 的长为 4 或 7 .
4
【总结】本题应注意多解问题的存在性,也可采用锐角三角比进行求解.
【练习 37】如图,在?AOB 中,已知?AOB ? 90? ,AO = 3,BO = 6,将?AOB 绕顶点 O 逆时针旋转到?A'OB ' 处,此时线段 A' B ' 与 BO 的交点 E 为 BO 的中点,那么线段 B ' E 的
长度为 .
【难度】★★★
【答案】 9 5 .
5
【解析】作OF ? A' B ' 交 A' B ' 于点 F ,根据勾股定理可得:
A
F
B E O
AB ?
AO2 ? BO2 ? 3 5 ,根据面积法可得: OF ? AO ? BO ? 6 5 ,
2663085-117558AB 5
勾股定理可得:EF ?
? 3 5 ,根据旋转性质tan B ? OA ? 1 ? tan B ' ? OF ,
EO2 ? OF 2
5
由此可得: B ' F ? 12 5 , B ' E ? B ' F ? EF ? 9 5 .
OB 2
B ' F
5 5
【总结】考查旋转性质的综合应用.
【练习38】如图,在直线m 上摆放着三个正三角形:?ABC 、?HFG 、?DCE ,已知 BC ? 1 CE ,
2
F、G 分别是 BC、CE 的中点,FM // AC,GN // DC.设图中三个平行四边形的面积依次是 S1 、 S2 、 S3 ,若 S1 ? S3 ? 10 ,则 S2 ???.
【难度】★★★ D
【答案】4. H
【解析】设CD 与GH 交点为 P , A N
由 AB / /FH / /CD ,可得: S1 ? AM ? CF ? 1 , M P
S2 CP CG 2
即得: S
? 2S ,同理可得 S2 ? 1 ,
2 1
3
B F C G E
S
2
则有 S3 ? 2S2 ? 4S1 ,由 S1 ? S3 ? 10 ,可得: S1 ? 2 ,则 S2 ? 2S1 ? 4 .
【总结】考查平行线分等边三角形也得到等边三角形以及面积等比的转化.
【练习 39】如图,在矩形 ABCD 中,已知 AB = 12,AD = 8,如果将矩形沿直线 l 翻折后点
A 落在边 CD 的中点 E 处,直线 l 分别与边 AB、AD 交于点 M、N,那么 MN = .
【难度】★★★
【答案】
125 .
12
A M D
【解析】连结 ME ,依题意可得 MN 垂直平分 AE ,则有 AM ? ME , N E
设 AM ? x ,则有 ME ? x , AD ? 8 ? x ,
在 Rt?DME 中用勾股定理,则有 DM 2 ? DE2 ? ME2 ,
l B C
即?8 ? x?2 ? 62 ? x2 ,解得: x ? 25 , MN ? AE , ?BAD ? 90? ,易得?DAE ? ?ANM ,
AD2 ? DE2
4
勾股定理得: AE ?
? 10 ,则有sin ?DAE ? DE ? 3 ? sin ?ANM ? AM ,
25
即 4 ? 3 ,得: MN ? 125 .
AE 5 MN
MN 5 12
【总结】考查翻折的性质和锐角三角比的综合应用.
【练习 40】如图,在矩形 ABCD 中,AB = 8,BC = 9,点 P 在 BC 边上,CP = 3,点 Q 为线
段 AP 上的动点,射线 BQ 与矩形 ABCD 的一边交于点 R,且 AP = BR,则 QR ? .
BQ
【难度】★★★
【答案】1 或 4 ?
8
19 .
A R D
AB2 ? BP2
【解析】由 BC = 9,CP = 3,可得 BP ? BC ? CP ? 6 , Q
勾股定理可得: AP ?
? 10 ? BR .
B P C
(1)当射线 BQ 与 AD 交于点 R 时,可得 AR ? BP ? 6 ,由 AD / /BC ,则有 QR ? AR ? 1 ;
BQ BP
(2)射线 BQ 与CD 交于点 R ,延长 AP 交 DC 延长线于点 E ,
D
R
P
C
Q
BR2 ? BC2
A
35057418931勾股定理可得: CR ? ? 19 ,由 AB / /CD ,
则有 BP ? AB ,即 6 ? 8
,得CE ? 4 ,
CP CE 3 CE
由此可得: QR ? RE ? 4 ?
BQ AB 8
19 . B
E
【总结】考查三角形一边平行线性质定理的综合应用,注意题目的多解性.
解答题
【练习 41】(1) 2
tan 30?
? 2sin 60?cos 45? ? 3tan 30?sin 45? .
tan 70? tan 20? ? 4cos30? ? 4cos2 30?
(2) tan2 30? ? 2 tan 30? ?1 ? .
【难度】★★
【答案】(1) 2
? tan 60? ? 3tan 45? ? cot 40? cot 50? ? 8 sin2 60? .
?1 ? tan 60??2
3
3
;(2) 2 ? 4 3 ;(3)1.
3
【解析】(1)原式?
2 ? 2 ? 3 ? 2 ? 3? 3 ? 2 ? 2 3 ;
4305769-1168353 2 2 3 2
3
?
3 ? ?
3
4 3
?
(2)原式? 1 ? tan 30? ? 2cos 30? ?1 ? ?1 ? 3 ? ? ? 2 ? 2 ?1? ? 2 ? 3 ;
? ? ? ?
8 ? 3 ?2
284981174305447289584605521015984605(3)原式? tan 60? ?1 ?
3 ? 3?1 ? 1 ? 3 ? ? 2 ?
? ? 3 ?1?? ?3 ?
3 ??1 ? 1 .
? ?
【总结】考查特殊角锐角三角比的计算,去绝对值注意符号.
A
D
F
E
B
G
C
【练习 42】如图,D、E 是?ABC 边 AB 上的点,F、G 分别是边
AC、BC 上的点,且满足 AD = DE = EB,DF // BC,EG // AC.
(1)求证:FG // AB;
1902106-315242455826-315243544402-315243790535-315244436711-31524(2)设CA ? a , CB ? b ,请用向量a 、b 表示向量GF .
【难度】★★
2636572216923
【答案】(1)略;(2) GF ? 2 ?a ? b?.
【解析】(1)证明:
DF / /BC ,? DF ? AD ? 1 ,即 DF ? 1 BC ,
2344851-113447BC AB 3 3
1410766135354EG / / AC ,? BG ? BE ? 1 ,即 BG ? 1 BC ,
BC AB 3 3
2477566115193?BG ? DF . BG / /DF , ?四边形 BGFD 是平行四边形.
?FG / BD ,即 FG / / AB ;
(2)由(1)可得: BG ? BE ? 1 ,又 FG / / AB ,则有 FG ? CG ? 2 ,
BC AB 3 AB BC 3
170270347092 3 3 3
即得GF ? 2 BA ? 2 ?CA ? CB?? 2 ?a ? b?.
【总结】考查三角形一边平行线性质定理的综合应用,同时考查同向向量的意义和向量的线性运算.
【练习 43】如图, ?ABC 中,AC = BC,F 为底边 AB 上一点, BF ? m (m、n > 0),D 是
AF n
CF 中点,联结 AD 并延长交 BC 于 E.
A
F
D
C
E
G
B
(1)求 BE 的值;
EC
(2)若 BE = 2 EC,求证: CF ? AB .
【难度】★★
【答案】(1)
m ? n n
;(2)略.
【解析】(1)过点 F 作 FG / /DE 交 BC 于点G ,
则有 BG ? BF ? m ,又 D 为 CF 中点,可知 E 为GC 中点,
GE AF n
由此可得: BE ? m ? n ;
CE n
(2)证明:BE = 2 EC,则有 BE ? m ? n ? 2 ,
CE n
由此可得: m ? n ,则有 AF ? FB ,即 F 为 AB 中点.
141076587587AC ? BC ,?CF ? AB .
【总结】考查三角形一边平行线性质定理的综合应用,作平行线构造“A”字型和“8”字型等基本图形进行比例变换即可.
【练习 44】在平行四边形 ABCD 中,点 E 在 BC 边上,点 F 在 BC 边的延长线上,且 BE = CF.
5445658343916(1)求证:四边形 AEFD 是平行四边形;
(2)连接 AF,分别交 DE、CD 于 M、N,若?B??AME
A D
M
N
B
E
C
F
【难度】★★
【答案】略.
【解析】证明 四边形 ABCD 是平行四边形,
291063589978? AD / /BC , AD ? BC , BE ? CF ,
?EF ? EC ? CF ? EC ? BE ? BC ? AD ,
?四边形 AEFD 是平行四边形;
(2)四边形 ABCD 是平行四边形,??B ? ?ADC .
,求证:ND AD ? AN ME .
1410767108434?AME ? ?DMN , ?B ? ?AME , ??ADN ? ?DMN .
?MND
? ?DNA ,??ADN ∽ ?DMN ,? AN ?
AD .
14107656828MD ? ME ,?ND ? AD ? AN ? ME .
DN DM
【总结】考查平行四边形性质和相似的结合应用.
D C
E
O
A
B
【练习 45】如图,梯形 ABCD 中,AB // CD,AD = BC,点 E 在边 AD 上,BE 与 AC 相交于点 O,且?ABE ? ?BCA .
37145375889求证:(1) ?BAE ∽ ?BOA ;(2) BO BE ? BC AE .
【难度】★★
【答案】略.
【解析】证明 四边形 ABCD 是等腰梯形,
??DAB ? ?ABC .
141076789978?ABE ? ?BCA , ?OAB ? ?BAC ,
??AOB ∽ ?ABC .
??AOB ? ?ABC ? ?DAB .
141076890428?ABO ? ?ABE , ? ?BAE ∽ ?BOA ;
(2)由?BAE ∽ ?BOA ,则有 AE ? BE ,
? B E ? A .
OA AB
由?AOB ∽ ?ABC ,则有 OA ? OB ,
AB BC
A E O
5087407135350? BE ? BC ,即证 BO BE ? BC AE .
AE BO
【总结】考查相似三角形的判定,先判定在应用进行等比转换.
【练习 46】如图,在?ABC 中, ?ACB ? 90? ,点 D 在边 AB 上,DE 平分?CDB 交边 BC
C
E
A
D
M
B
于点 E,EM 是线段 BD 的垂直平分线.
(1)求证: CD ? BE ;
BC BD
(2)若 AB = 10,cos B = 4 ,求 CD 的长.
5
【难度】★★
【答案】(1)略;(2)5.
EM
【解析】证明:(1)
是线段 BD 的垂直平分线,
?BE ? DE , ?B ? ?EDB .
141076787580?EDB ? ?CDE ,??CDE ? ?B .
1410767109805?DCE ? ?BCD ,
??CDE ∽ ?CBD ,? CD ? DE ? BE .
BC BD BD
(2)由cos B ? BC ? 4 ,可得: BC ? 8 ,同时cos B ? BM ? 4 ,即得: BE ? BE ? 5 ,
AB 5
BE 5
BD 2BM 8
? CD ? BE ? 5 ,即得CD ? 5 .
BC BD 8
【总结】考查锐角三角比在直角三角形中的综合应用.
【练习 47】如图,在?ABC 中, ?BAC ? 90? ,AD 是 BC 边上的高,点 E 在线段 DC 上,
EF ? AB,EG ? AC,垂足分别为 F,G.求证:(1) EG ? CG ;(2) FD ? DG .
AD CD
A
F
G
B
D E
C
【难度】★★
【答案】略.
1944142126317【解析】(1) EG ? AC , AD 是边 BC 上的高,
??ADC ? ?EGC ? 90? ?C ? ?C ,
??E G C∽
?A D C,
? EG ? CG .
AD CD
1478052153421(2)
?BAC ? 90? , EF ? AB , EG ? AC ,?四边形是 AFEG 矩形,
? AF ? EG .
EG ? CG ,
AD CD
? AF ? AD .
CG CD
1410742153622EG ? AC , AD 是边 BC 上的高,即有?DAC ? ?DAF ? 90?,?DAC ? ?C ? 90? ,
??DAF ? ?C , ??FAD ∽ ?GCD ,
??FDA ? ?GDC ,
? FD ? DG .
? ?F D A ? ?G D A? ? G D C? ? ,即?FDG ? ?ADC ,
【总结】考查相似三角形判定定理 1 与定理 2 和相似三角形性质的综合题,需要根据题目需求进行变形,找准题目所求结论,然后根据性质和判定进行灵活转换.
【练习 48】据新华社 2014 年 12 月 13 日电,参加湄公河联合巡逻执法的中国巡逻船顺利返航.已知在巡逻过程中,某一天上午,我巡逻船正在由西向东匀速行驶,10:00 巡逻船在 A 处发现北偏东 53.1°方向,相距 10 海里的 C 处有一个不明物体正在向正东方向移动,10:15 巡逻船在 B 处又测得该物体位于北偏东 18.4°方向的 D 处.若巡逻船的速度是每小时 36 海里.
(1)试在图中画出点 D 的大致位置,并求不明物体移动的速度;
(2)假设该不明物体移动的方向和速度保持不变,巡逻船航行的方向和速度也不变,试问什么时间该物体与我巡逻船之间的距离最近?
(备用数据:sin 53.1?? 0.8 ,cos53.1?? 0.6 ,cot 53.1?? 0.75 ,sin18.4?? 0.32 ,cos18.4?? 0.95 ,
cot18.4?? 3 )
【难度】★★★
【答案】(1) D 点位置如图,不明物体移动速度为每小时 12 海里;(2)10:20 该物体与巡逻船距离最近.
【解析】(1) B 点北偏东 18.4° 即为 D 点位置,如图所示, ?EBD ? 18.4? ;
作CF ? AB 交 AB 于点 F ,则有CF ? BE ,
则有?ACF ? 53.1? ,由此可得 AF ? AC ? sin ?ACF ?10? 0.8 ? 8 ,
CF ? AC ? cos?ACF ?10? 0.6 ? 6 ? BE ,
C E D
由此可得: DE ?
BE
cot ?EBD
? 6 ? 2 ,
3
A F B
巡逻船速度为每小时 36 海里,可得 AB ? 15 ? 36 ? 9 ,则有 FB ? AB ? AF ?1 ? CE ,
60
则CD ? CE ? ED ? 3 ,不明物体速度为3 ? 15 ? 12 海里/小时;
60
(2)两物体距离最近,巡逻船正好在不明物体的下方,转化为追及问题,可知巡逻船行驶时间为8 ? ?36 ?12? ? 1 h ? 20 min ,即 10:20 时该物体与我巡逻船距离最近.
3
【总结】考查方位角和锐角三角比在实际问题中的应用,把相应的长度转化为直角三角形的边长即可.
【练习 49】如图,在?ABC 中, ?C ? 90? ,AC = 4,BC = 3,O 是 AB 上一点, 且 AO : OB = 2 : 5.
(1)过点 O 作OH ? AC 垂足为点 H,求点 O 到直线 AC 的距离 OH 的长;(图 1)
(2)若 P 是边 AC 上的一个动点,作 PQ ? OP 交线段 BC 于点 Q(不与 B、C 重合)(图 2)
①求证: ?POH ∽ ?QPC ;
②设 AP = x,CQ = y,试求 y 关于 x 的函数解析式,并写出定义域;
③当 AP 为何值时,能使?OPQ 与?CPQ 相似.
C
H
B
O
A
图 1
C
Q
P
H
B
O
A
图 2
【难度】★★★
【答案】(1) 6 ;
7
(2)①略;
② y ? ? 7 x2 ? 6x ? 16 ,
6 3
定义域为 8 ? x ? 4 ;
7
③ 26 或10 或18 .
7 7 7
【解析】(1)由OH ? AC , ?C ? 90? , 可得OH / /BC ,则有 OH ? OA ? 2 ,
由此可得: OH ? 6 ;
16120612141927
BC AB 7
(2)①
?OPQ ? 90? ,??CPQ ? ?OPH ? 90? .
?C ? 90? ,??CPQ ? ?CQP ? 90? .
4088561-164080259948889284??CPQ ? ?OPH . ?C ? ?PHO ? 90? , ? ?POH ∽ ?QPC ;
② ?POH ∽ ?QPC ,则有 PH ? OH ,由 tan A ? BC ? 3 ? OH ,可得: AH ? 8 ,
CQ PC AC 4 AH 7
x ? 8 6
则有 PH ? x ? 8 ,CP ? 4 ? x ,即得 7 ? 7 ,整理得:y ? ? 7 x2 ? 6x ? 16 ? 8 ? x ? 4 ? ;
7 y 4 ? x
6 3 ? 7 ?
? ?
③ ?POH ∽ ?QPC ,则有 OP ? OH ,若?OPQ 与?CPQ 相似,则应有 OH ? PH 或
PQ CP
6 6
6 x ? 8
PC OH
OH ? OH ,即可得: 7 ?
??
7 或 7 ?
?
7 ,分别解得: x ? 18 , 10 , 26 .
PC PH
4 ? x x ? 8
7
4 ? x 6
7
7 7 7
【总结】相似的分类讨论只需要转化为一个三角形中的边的关系即可,分类时要注意变化顺序.
【练习 50】如图,在平面直角坐标系中,点 A、C 分别在 x 轴,y 轴上,四边形 ABCO 为矩
形,AB = 16,点 D 与点 A 关于 y 轴对称, tan ?ACB ? 4 ,点 E、F 分别是线段 AD、
3
AC 上的动点(点 E 不与点 A、D 重合),且?CEF ? ?ACB .
(1)求 AC 的长和点 D 的坐标; y
(2)说明?AEF 与?DCE 相似; B C
(3)当?EFC 为等腰三角形时,求点 E 的坐标.
G
【难度】★★★
F
【答案】(1) AC ? 20 , D ?12,0?;(2)略;
? 14 ?
A O E D x
3
(3) ?8,0? 或? ,0 ? .
? ?
【解析】(1)由 AB = 16, tan ?ACB ? 4 ,可得: BC ?
3
AB
tan ?ACB
? 12 ,勾股定理可得
AB2 ? BC2
AC ?
? 20 ,同时可得: AO ? BC ?12 ,则有 A??12,0? ,点 D 与点 A 关于
y 轴对称,可知 D ?12 ,0? ;
(2) CO ? AD,AO ? OD ,可得: AC ? CD ,则有?CAO ? ?CDO ,又 BC / / AO , 得?CAO ? ?ACB ? ?CEF ,由外角可得?CEA ? ?ECD ? ?CDE ? ?CEF ? ?AEF , 由此可得: ?ECD ? ?AEF ,即证?AEF ∽ ?DCE ;
(3)由(2)可得: ?CEF ? ?CAE ,由?FCE ? ?ACE ,可得?EFC ∽ ?AEC , ?EFC 为等腰三角形,即为?AEC 等腰三角形,由此进行分类讨论:
① AE ? AC 时,则有 AE ? 20 , EO ? 8 ,即得 E 点坐标?8,0? ;
② AE ? CE 时,作 EG ? AC 交 AC 于点G ,则有 AG ? 1 AC ? 10 ,
2
此时 tan ?GAE ? tan ?BCA ? 4 ? GE ,则GE ? 40 ,
勾股定理得: AE ?
3 AG 3
AG2 ? GE2
? 50 ,
3
此时 EO ? 14 ,即得: E 点坐标? 14,0 ? ;
3 ? 3 ?
? ?
③ CE ? AC 时,此时 D 、 E 重合,不符合题意,即不存在; 综上所述,点 E 坐标为?8,0? 或? 14,0 ? .
? 3 ?
? ?
【总结】(2)考查利用“一线三等角”基本模型证相似,(3)中的等腰三角形问题通过转化找到简单易算的三角形进行分类讨论即可.
【练习 51】在平行四边形 ABOC 中, AO ? BO ,且 AO = BO,以 AO、BO 所在直线为坐标轴建立如图所示的平面直角坐标系,已知 B( ?6 ,0),直线 y = 3x + b 过点 C 且与 x轴交于点 D.
(1)求点 D 的坐标;
(2)点 E 为 y 轴正半轴上一点,当?BED ? 45? 时,求直线 EC 的解析式;
(3)在(2)的条件下,设直线 EC 与 x 轴交于点 F,ED 与 AC 交于点 G.点 P 从点 O 出发以每秒 1 个单位的速度沿折线 OF—FE 运动,在运动过程中直线 PA 交 BE 于 H,设运动时间为 t.当以 E、H、A 为顶点的三角形与?EGC 相似时,求 t 的值.
【难度】★★★
【答案】(1) D ?4,0? ;(2) y ? ?x ?12 ; (3)6 或15 2 ? 12 .
2
【解析】(1)由 AC ? BO ? AO ,B( ?6 ,0),可得: C ?6,6? ,直线 y = 3x + b 过点 C,
则有3? 6 ? b ? 6 ,得: b ? ?12 ,
令 y ? 3x ?12 ? 0 ,得: x ? 4 ,即得 D ?4,0? ;
(2)设 E ?0,a? ,过点O 作OM / /BE 交 DE 于点 M ,
B
则有?OMD ? ?BED ? 45? ,
由此可得: ?OME ?135? ? ?BAE ,
y E
A G C M
O D F x
根据外角可知?BAO ? ?ABE ? ?BEA ? 45? , ?BED ? ?BEA ? ?AED ? 45? , 所以?ABE ? ?MEO .
BO2 ? OE2
a2 ? 36
由此 ?BAE ∽ ?EMO ,则有 BE ? AE ,勾股定理可得 BE ? ? ,
OM OD 4 2
OE MO
2 2
a ? 6
a2 ? 36
又 ? ? ? ,可得OM ?
BE
a ? 36 ,代入即为
? 2 ,
a2 ? 36
DB 10 5 5 a
5
整理得: a2 ?10a ? 24 ? 0 ,解得: a ? 12 , a ? ?2 (舍),即得 E ?0,12?,
1 2
由此可设CE : y ? kx ?12 过点C ?6,6?,则有6k ?12 ? 6 ,得: k ? ?1,
由此可知直线 EC 解析式为: y ? ?x ?12 ;
(3)分类讨论:①点 P 在OF 上运动时,由CE : y ? ?x ?12 ,可得: F ?12 ,0?,则有
?OFE ? ?ACE ? ?AEC ? 45? ,由此可得?HEA ? ?GEC , ?EHA 与?EGC 相似, 则应有?EAH ? ?ECG ? 45? ,由此可得?OAP ? ?EAH ? 45? , OP ? OA ? 6 ,
P 点运动时间t ? 6 ?1 ? 6s ;
②点 P 在 EF 上运动时,由CE : y ? ?x ?12 ,可得: F ?12 ,0?,
则有?OFE ? ?ACE ? ?AEC ? 45? ,
同①可得?HEA ? ?GEC , ?EHA 与?EGC 相似,
则应有?EHA ? ?ECG ? 45? ,由?BED ? 45? ,可得: DE ? PH ,
可得:直线 PH 解析式为 y ? 1 x ? 6 ,令 y ? 1 x ? 6 ? ?x ? 12 ,
3 3
解得 x ? 9 ,即 P ? 9 15 ? ,
? , ?
2 ? 2 2 ?
? 9 ?2 ? 15 ?2
?12 ? 2 ? ? ? 2 ?
?
? ? ?
15 2
由此根据勾股定理可得 PF ? ? ,
2
由此可知点 P 运动时间为: ? 2
? 12? ?1 ?
? 15 2
? 15 2
? ?
2
?
?
12? s .
? ? ? ?
【总结】考查由角的转化构造找相似三角形的问题.
内容分析
本讲整理了关于前两章相似三角形和锐角三角比的相关练习,以帮助同学们巩固所学.
知识结构
三角形一边的平行线
性质定理及推论
平行线分线段
成比例定理
比例线段
比例的性质
三角形一边的平行线
相
似形
判定定理及推论
相似三角形的概念
相似三角形
相似三角形的预备定理
相似三角形的判定定理
相似三角形的性质定理
运算法则
平行向量定理
实数与向量相乘
运算律
向量的线性组合
向量的线性运算
向量的分解
已知锐角,求三角比
锐角的三角比的概念
已知锐角的三角比,求锐角
已知一边和一个锐角
直角三角形中
的边角关系
解直角
三角形
已知两边
解直角
三角形的应用
选择题
【练习 1】已知在?ABC 中, ?C ? 90? , ?A ? ? ,AC = 3,那么 AB 的长为( )
A. 3sin? B. 3cos? C. 3
sin ?
D. 3 cos?
【难度】★
【答案】D
【解析】根据锐角三角比的概念,可得cos A ? AC ,即得: AB ?
AB
AC ?
cos A
3 .
cos?
【总结】本题主要考查锐角三角比的概念.
3
3
? 1 ?2
2
【练习 2】在?ABC 中,若? sin A ? ?
? ?
cot B ? ? 0 ,则?ABC 的形状是( )
A.等边三角形 B.直角三角形 C.锐角三角形 D.钝角三角形
【难度】★
【答案】B
3
3
3
? 1 ?2 1
2
【解析】由? sin A ? ?
? ?
cot B ? ? 0 ,即可得sin A ? ,cot B ?
2
,由此可得?A ? 30? ,
3
?B ? 60? ,则?C ?180? ? ?A ? ?B ? 90? ,故选 B.
【总结】本题主要考查两非负数相加和为 0,则两个数均为 0 的知识点,结合特殊角的锐角三角比进行计算.
【练习 3】已知在?ABC 中, ?C ? 90? ,设 cos B = n,当?B 是最小的内角时,n 的取值范围是( )
A. 0 ? n ? 2
2
B. 0 ? n ? 1
2
C. 2 ? n ? 1
2
【难度】★
【答案】C
D. 1 ? n ? 1
2
【解析】?B 是最小内角,则0? ? ?B ? 45? ,根据余弦值的增减性, cos B ? cos 45? ? 2 ,
2
根据0 ? cos B ? 1,故选 C.
【总结】本题主要考查锐角三角比的增减性.
315350510114452817621011446059901101144【练习 4】如果向量a 与单位向量e 方向相反,且长度为 1 ,那么向量a 用单位向量e 表示
2
a ? 1 e
为( )
A.
2
B. a ? 2e
a ?? 1 e
5670367-30719C. D. a ? ?2e
2
2995589-299341【难度】★
【答案】C
304886297755【解析】方向相反,即可表示为a ? ?ne ?n ? 0?,长度为 1 ,可得n ? 1 ,故选 C.
2 2
【总结】考查平行向量的表示.
397346132490453840532490539341132490【练习 5】如图,在平行四边形 ABCD 中,如果 AB ? a , AD ? b ,那么 a ? b 等于( )
D
C
A
B
1665861-318832724818-318873791841-318834866258-31887A. BD B. AC C. DB D. CA
【难度】★
【答案】B
3686891-30781【解析】根据向量的“平行四边形法则”,得 AB ? AD ? AC .
【总结】考查向量运算的“平行四边形”法则.
【练习 6】下列不等式中正确的个数是( )
① sin 47? ? sin 48? ;② cos70? ? sin 30? ;③ tan 55? ? cot 55? ;④ cos 46? ? sin 46? ;
⑤ sin80? ? cot 42? .
A.1 个 B.2 个 C.3 个 D.4 个
【难度】★★
【答案】A
【解析】根据正弦值增减性,锐角正弦值随着角度增大而变大,①错误; cos70? ? sin 20? ,
②错误;锐角正切值随着角度增大而变大,cot 55? ? tan 35? ,③正确;cos46? ? sin 44? ,
④错误; cot 42? ? tan 48? ? tan 45? ?1, 0 ? sin80? ?1,⑤错误;③正确,故选 A.
【总结】考查锐角三角比的转化和相关增减性.
【练习 7】如图,已知 AD // BC,AC 与 BD 相交于点 O,点 G 是 BD 的中点,过点 G 作
GE // BC 交 AC 于点 E,如果 AD =1,BC = 3,那么 GE : BC 等于( )
A D
O
G E
B
C
A.1 : 2 B.1 : 3 C.1 : 4 D.2 : 3
【难度】★★
【答案】B
【解析】根据三角形一边平行线的性质定理,可得: DO ? AD ? 1 ,
BO BC 3
点G 是 BD 中点,可得: DO ? GO ,则有 AD ? DO ? 1,
GE GO
则有GE : BC ? AD : BC ?1: 3 .
【总结】考查三角形一边平行线性质定理的应用.
【练习 8】下列命题正确的个数有( )个
(1)长度相等的两个非零向量相等
(2)平行向量一定在同一直线上
(3)与零向量相等的向量必定是零向量
(4)任意两个相等的非零向量的始点与终点是一平行四边形的四个顶点
A.0 个 B.1 个 C.2 个 D.3 个
【难度】★★
【答案】B
【解析】相等的向量需确保方向相同,(1)错误;平行向量是同一平面内平行的两条有向线段,不一定在同一直线上,(2)错误;只有零向量模长为 0,可知与零向量相等的必定是零向量,(3)正确;相等向量可以在同一直线上,此时四个点不能构成四边形,
(4)错误.综上所述,只有(3)正确,故选 B.
【总结】考查与向量有关的相关定义的理解和把握.
3
3
3
【练习 9】如图,已知边长为 5 的等边三角形 ABC 纸片,点 E 在 AC 边上,点 F 在 AB 边上, 沿着 EF 折叠,使点 A 落在 BC 边上的点 D 的位置,且 ED ? BC ,则 CE 的长是( )
178669346688A.10 3 ?15
B.10 ? 5
C. 5 ? 5
D. 20 ?10
A
E
F
B
D
C
【难度】★★
【答案】D
【解析】是等边三角形,则有?C ? 60? ,由 ED ? BC ,
可得: DE ? CE ? sin C ?
3 CE ,翻折可得 AE ? DE ,
2
27204651276203
? 3 ?
即有 AC ? AE ? CE ? ? ? 1?CE ? 5 ,得: CE ? 20 ?10 .
? 2 ?
【总结】考查特殊图形结合特殊锐角三角比的相关应用.
【练习 10】如图,已知 AD 是等腰?ABC 底边上的高,且tan ?B ? 3 ,AC 上有一点 E,满
4
足 AE : CE = 2 : 3,则 tan ?ADE 的值是( )
A. 9
8
【难度】★★
【答案】C
B. 4
5
C. 8
9
D. 7
9
B
A
F E D
C
【解析】作 EF ? AD 交 AD 于点 F ,
EF AF AE 2
则有 EF / /CD , ? ? ? ,
CD AD AC 5
因为?ABC 是等腰三角形,则有 tan C ? tan B ? 3 ,设 AD ? 3a ,则CD ? 4a ,
4
由此可得: AF ? 6 a , EF ? 8 a ,则 DF ? AD ? AF ? 9 a , tan ?ADE ? EF ? 8 .
5 5 5 DF 9
【总结】考查相似三角形和相关锐角三角比的应用,通过作高把所求锐角放到直角三角形中即可.
【练习 11】如图,D、E 分别是?ABC 的边 AB、AC 上的点,且 DE // BC,BE 交 DC 于点 F, EF : FB = 1 : 3,则 S?ADE : S?BCF 的值为( )
A.1 : 9 B.1 : 3 C.2 : 9 D.1 : 7
【难度】★★
A
D
E
F
B
C
【答案】C
【解析】由 DE // BC,即得:DE ? EF ? 1 ? AD ,则有 AD ? 1 ,
BC FB 3 AB DB 2
设 S ? a ,则 S
? 2a ,由 EF ? 1 ,即可得 S
? 1 a ,
?ADE
S ? EF ?2 1
?BDE
FB 3
9
?DEF 2
又 ?DEF ? ?
,即得: S? ? a .
? ?
FB
S?BCF ? ? 9
BCF 2
由此可得: S
?ADE
: S?BCF
? a : a
9
2
? 2 : 9 .
【总结】考查三角形一边平行线性质定理的应用,“A”字型和“8”字型的叠合应用,同时注意等高三角形面积和相似三角形面积比与相应边长的关系.
【练习 12】在一次夏令营活动中,小智从位于 A 点的营地出发,沿北偏东 60°方向走了 5 km
到达 B 地,然后再沿北偏西 30°方向走了若干千米到达 C 地,测得 A 地在 C 地南偏西
38546063728333
30°方向,则 A、C 两地的距离为( )km
A. 10 3
3
【难度】★★
【答案】A
B. 5 3
3
C. 5 2 D. 5
4854575-355264【解析】依题意可得到如图所示的图形,则有?BAE ? 60? ,
?2 ? ?3 ? 30? ,由 EF / /MN / /PQ ,可得: ?2 ? ?4 ? 30? ,
?1 ? ?BAE ? 60? ,则有?ABC ?180? ? ?1? ?2 ? 90? ,
?5 ? ?EAB ? ?CAE ? 30? ,则有?ACB ? 60? ,
由此可得: AB ? sin ?ACB ,又 AB ? 5 ,
AC
即得: AC ?
AB
sin 60?
? 10 3 km .
3
【总结】考查方位角知识的综合应用,结合特殊角的锐角三角比进行求解计算.
【练习 13】如图,小方同学在晚上由路灯 AC 走向路灯 BD,当他走到点 P 时,发现身后他影子的顶部刚好接触到路灯 AC 的底部,当他向前再步行 20 m 到达 Q 点时,发现身前他影子的顶部刚好接触到路灯 BD 的底部,已知小方的身高是 1.5 m,两个路灯的高度都是 9 m,则两路灯之间的距离是( )米
A.20 B.25 C.30 D.35
C
D
A P
Q B
【难度】★★
【答案】C
【解析】设 AP ? x ,依题意可得: BQ ? AP , 1.5 ? AP ,
BD AB
1.5 ?
x ,解得: x ? 5 ,则 AB ? 20 ? 2x ? 30 ,
9 2x ? 20
故选 C.
【总结】考查三角形一边平行线性质定理的实际应用.
【练习 14】如图,在 Rt?ABC 中, ?ABC ? 90? ,BA = BC,点 D 是 AB 的中点,连接 CD, 过点 B 作 BG ? CD ,分别交 CD、CA 于点 E、F,与过点 A 且垂直于 AB 的直线相交于点 G,连接 DF.给出以下四个结论:
AG ? FG ;(2)点 F 是 GE 的中点;(3) AF ?
AB FB
其中正确的个数有( )
2 AB ;(4) S
3
?ABC
? 5S
?BDF ,
A.1 个 B.2 个 C.3 个 D.4 个
C
G
F
E
A
D
B
【难度】★★★
【答案】B
【解析】由?BAG ? ?ABC ? 90? , ?ABG ? ?BCD , AB ? AC ,
可得: ?ABG ? ?BCD ,且有 AG / /BC ,则有 AG ? BD ? 1 BC ,
2
由此可得: AF ? GF ? AG ? 1 ,可知(1)正确;同时, CD 不
CF BF BC 2
是?ACB 的角平分线,可得 BE ? FE ,则 F 不是 GE 中点,
(2)错误;此时可得 AF ? 1 AC ? 2 AB ,(3)正确;则有 S
? 3S
? 6S ,
3 3
(4)错误;综上所述,正确的是(1)(3),故选 B.
?ABC
?ABF
?BDF
【总结】考查等腰直角三角形结合平行问题中特殊边角关系的综合应用.
【练习 15】如图,在正方形 ABCD 中,点 P 是 AB 上一动点(不与 A、B 重合),对角线 AC、
BD 相交于点 O,过点 P 分别作 AC、BD 的垂线,分别交 AC、BD 于点 E、F,交 AD、
BC 于点 M、N,下列结论:
(1)?APE ≌ ?AME ;(2)PM ? PN ? AC ;(3)PE2 ? PF 2 ? PO2 ;(4)?POF ∽ ?BNF ;
(5)当?PMN ∽ ?AMP 时,点 P 是 AB 的中点. 其中正确的结论有( )
A.5 个 B.4 个 C.3 个 D.2 个
【难度】★★★
M D
【答案】B
【解析】根据正方形的性质,即可得?PAE ? ?MAE ? 45? , E
P
由 PM ? AE , AE ? AE ,可得?APE ≌ ?AME ,(1)正确; O
36018961296924441621129692同理可得?PBF ? ?NBF ,则有 PM ? 2AP , PN ? 2PB , F
N C
237443434623325426134623则有 PM ? PN ? 2 ?PA ? PB? ? 2AB ? AC ,(2)正确;
由?AOB ? 90? ,可知四边形 PEOF 是矩形,则有 PE2 ? PF 2 ? PO2 ,(3)正确;?BNF
为等腰直角三角形, ?POF 是直角三角形,但不能确定为等腰,(4)错误; ?PMN ∽
318204366575365235866575?AMP 时,则有 PM ? PN ,即 2AP ? 2BP ,由此可得 AP ? BP ,P 为 AB 中点,(5)
正确;综上所述,正确的是(1)(2)(3)(5),故选 B.
【总结】本题综合性较强,主要考查正方形性质的综合应用,注意题目中由正方形得到的边角关系,从而利用勾股定理完成解题.
填空题
【练习 16】? 为锐角,(1)sin? ? 2 ,则 tan ? ?
3
;(2)cot? ? 3,则sin ? ? .
【难度】★
【答案】(1) 2 5 ;(2) 10 .
5 10
【解析】(1)由sin2 ? ? cos2 ? ? 1 ,可得: cos? ?
5 ,则tan? ? sin? ?
2 ? 2 5 ;
5
3 cos??5
(2)由cot ? ? cos? ? 3 ,可得cos? ? 3sin? ,又sin2 ? ? cos2 ? ? 1 ,即10sin2 ? ? 1 ,
sin ?
即得: sin? ?
10 .
10
【总结】考查锐角三角比之间的相互关系的转化,或利用设“ k ”法表示长度进行求解.
1106424-8717651? 2sin ? cos ? ?
【练习 17】? 为锐角,且cos? ? 1 ,则 .
2
【难度】★
【答案】 3 ? 1 .
2
【解析】? 为锐角, cos? ? 1 ,可得: ? ? 60? ,则sin? ?
2
3 ,由此即可化简得
2
1 ? 2sin? cos? ?
sin2 ? ? cos2 ? ? 2sin? cos? ? sin? ? cos? ?
3 ?1 .
2
【总结】考查sin2 ? ? cos2 ? ? 1 公式的灵活运用进行锐角三角比化简,也可利用特殊角的锐角三角比的值进行计算求值.
【练习 18】在正方形网格中, ?ABC 的位置如图所示,则cos ?B 的值为 .
【难度】★
C
B
A
【答案】 2 .
2
【解析】由图中所示格点位置,知?B ? 45? ,则cos ?B ? 2 .
2
【总结】考查利用格点三角形得到相关角的锐角三角比.
【练习 19】如图,在正方形网格上有 6 个三角形:① ?ABC ;② ?CDB ;③ ?DEB ;④ ?FBG ;
⑤ ?HGF ;⑥ ?EKF ,在②~⑥中,与①相似的三角形是 (填序号).
C
D
E
A
K
B
G
H
F
【难度】★
【答案】③④⑤
【解析】由图示可得: ?BAC ? 135? ,且有
2
AC ? ,满足条件的图形只有③⑤.同时
AB
利用三边对应成比例,也可证得④成立.
【总结】考查“格点三角形”中根据勾股定理得到特殊边角关系和长度的应用.
【练习 20】已知 P 是线段 AB 的一个黄金分割点,且 AB = 20 cm,AP < BP,那么 AP = .
【难度】★★
2128519105592【答案】?30 ?10 5 ?cm .
【解析】根据黄金分割点的意义,由 AP < BP,可得 BP ?
27832222144693798735214469AP ? AB ? BP ? 20 ? ?10 5 ?10?? ?30 ?10 5 ?cm .
5 ?1 AB ? 10 5 ?10 ,则有
5305453-1399572
【总结】考查线段的黄金分割点和相应的黄金比,注意线段的黄金分割点有两个.
【练习 21】如果从灯塔 A 处观察到船 B 在它的北偏东 35°方向上,那么从船 B 观察灯塔 A
的方向是 .
【难度】★★
【答案】南偏西35? .
【解析】换位观察,方向变为相反,偏离角度大小不变,即得.
【总结】考查方位角的基本性质.
【练习 22】如图, ?ABC 中,?C ? 90? ,sin A ? 3 ,D 为 AC 上一点,且 BD = AC,DC = 7
5
B
A
D
C
cm,则 AD = .
【难度】★★
7
【答案】?4 ? 7?cm .
【解析】设 BC ? acm ,由sin
A ? 3 ,可得:AB ? 5 a ,AC ? 4 a ,
5 3 3
根据勾股定理可得 BD ?
? a2 ? 49 ? AC ? 4 a ,
BC2 ? CD2
7
46877902560823
7
即可解得: a ? 3
,则 AC ? 4
, AD ? AC ? DC ? ?4 7 ? 7?cm .
【总结】考查共直角边的两个直角三角形结合锐角三角比的应用,根据题目条件进行边角转换即可.
【练习 23】传送带和地面所成斜坡的坡度为 1 : 0.75,它把物体从地面送到离地面高 8 米的地方,物体在传送带上所经过的路程为 米.
【难度】★★
【答案】10.
【解析】传送带和地面所成坡度i ? 1: 0.75 ,可知物体传送的水平距离即为 8 ? 6m ,根据勾
i
82 ? 62
股定理即可得物体在传送带经过路程为
? 10m .
【总结】考查坡度的意义和应用.
A
B
C
【练习 24】如图,在坡度为 1 : 2.5 的楼梯表面铺地毯,已知楼梯高度 AC = 2 米,则地毯长度至少是 .
【难度】★★
【答案】7m .
【解析】楼梯的坡度为 1 : 2.5,可得楼梯水平长度
BC ? AC ? 5m ,则地毯长度至少为 2 ? 5 ? 7m .
i
【总结】考查坡度意义的综合应用,注意地毯要沿着楼梯铺设,完全覆盖.
53495061836025861708183602【练习 25】如图,正方形 ABCD 中,M 是边 BC 上一点,且 BM ? 1 BC .若 AB ?a
4
,AD ? b ,
170671232037195221032037233192732042A
D
B
M
C
试用a , b 表示 DM ???.
【难度】★★
【答案】a ? 3 b .
4
1667608-306504246260-30650【解析】DM ? DC ? MC ,根据正方形的性质,可得:DC ? AB ? a ,
1435750167978BC ? AD ? b ,由 BM ? 1 BC ,可得: BM ? 1 BC ? 1 b ,则有
4 4 4
MC ? 3 b , DM ? a ? 3 b .
4 4
【总结】考查平面向量的线性运算,注意把握好相等向量的定义.
【练习 26】如图,点 G 是?ABC 的重心, AG ? GC ,AC = 4,那么 BG 的长为 .
A
G
D
B
C
【难度】★★
【答案】4
【解析】延长 BG 交 AC 于点 D ,则 D 是 AC 中点,
1
由 AG ? GC ,则有GD ?
即可得 BG ? 2GD ? 4 .
AC ? 2 ,根据重心性质,
2
【总结】本题主要考查重心性质的应用.
【练习 27】如图,在梯形 ABCD 中,AD // BC,BE 平分?ABC 交 CD 于 E,且 BE ? CD ,
CE : ED = 2 : 1,如果?BEC 的面积为 2,那么四边形 ABED 的面积是 .
【难度】★★
【答案】 7 .
4
D H
F E
【解析】作 AG / /DC 交 BC 于点G ,交 BE 于点 F ,
延长 BE 交 AD 延长线于点 H . B G C
由 AD // BC,得?DEH ∽ ?CEB , ?DEH ∽ ?AFH ,
S ? DE ?2 ? 1 ?2 1 1
则 有 ?DEH ? ? ?
?
,可得: S? ? .
CE 2
S?CEB
? ? ? ?
? ? ? ? 4
DEH 2
由 BE ? CD , AG / /CD ,得 AF ? BH ,又 BE 平分?ABC ,则有 AF ? FG ? 1 AG ,
2
1 1 2
S ? DE ?2 ? 2 ?2 4 9
即得:DE ?
CD ? AG ?
?
AF ,由此可得: ?DEH ? ? ?
???
,得 S? ? ,
AF 3
3 3 3
S?AFH
? ? ? ?
? ? ? ? 9
AFH 8
由 AD // BC,BE 平分?ABC ,可知?ABH 为等腰三角形,
则有 S四边形ABED
? 2S
?AFH
S?DEH
? 2 ? 9 ? 1 ? 7 .
8 2 4
【总结】考查根据平行构造相似三角形“A”字型和“8”字型的应用,相似三角形面积比即为相似比的平方,同时考查平行线与角平分线得到等腰三角形的基本图形.
【练习 28】某学校为新生设计的学生板凳的正面视图如图所示,其中 BA = CD,BC = 20 cm,
BC、EF 平行于地面 AD 且到地面 AD 的距离分别为 40 cm、8 cm.为使板凳两腿底端 A、
D 之间的距离为 50 cm,那么横梁 EF = .(材质及其厚度等暂忽略不计).
B
C
E
F
A
P
Q
D
N
M
【难度】★★
【答案】44cm .
【解析】如图,分别延长 BM、CN 交 AD 于点 P 和点 Q. 在等腰梯形中易得 AP ? DQ , EM ? FN ,
由 BC / /EF / / AD ,即得: BC ? MN ? PQ ? 20 ,则有
AP ? 15 ,题中 BM ? 40 ? 8 ? 32 , BP ? 40 ,由 EF / / AD ,则有 EM ? BM ,
AP BP
即 EM ? 32 ,得 EM ?12 ? FM ,则 EF ? EM ? MN ? NF ? 44cm .
15 40
【总结】考查三角形一边平行线性质定理的实际应用.
【练习 29】如图,在?ABC 中,?A ? ? ,?B ? ? ,AB = c,用? 、? 、c 表示 S?ABC ???.
C
A
D
B
【难度】★★
c2 tan? tan ?
【答案】
2?tan? ? tan ? ? .
【解析】作CD ? AB 交 AB 于点 D ,
则有 tan A ? CD , tan B ? CD ,
由此可得 AD ?
AD CD
tan?
, BD ?
BD
CD
tan ?
, AB ? AD ? BD ,
即 CD
tan?
1
CD
?
tan ?
? c ,可得: CD ? c tan? tan ? ,
tan? ? tan ?
c2 tan? tan ?
则 S?ABC ? 2 CD ? AB ? 2?tan? ? tan ? ? .
【总结】考查锐角三角比性质的综合应用,通过作高实现边角转换.
3437445135161【练习 30】在 Rt?ABC 中,斜边 AB ? 2 5 , 且 tan A ? tan B ? 5 ,
2
则 Rt?ABC 的面积是 .
【难度】★★
【答案】4.
【解析】设两直角边长分别为 a 、b ,根据锐角三角比的定义,tan A ? tan B ? 5 ,即
b ? a ? 5 ,
a2 ? b2 5
2 2 2
2 a b 2
1
? ,由勾股定理可得a ? b
ab 2
? AB
? 20 ,则有ab ? 8 , S?ABC ? 2 ab ? 4 .
【总结】考查锐角三角比的基本定义结合勾股定理的应用.
【练习 31】已知:如图,AD 是?ABC 的中线,E 为 AD 上的一点,且 AE ? 1 ,射线 CE 交
ED k
AB 于 F, AF
FB
【难度】★★
A
???.
F E
【答案】 1 . G
2k
【解析】作 DG / /EF 交 AB 于点G ,则有 AF ? AE ? 1 ,
FG ED k
因为 D 为 BC 中点,且 DG / /CF ,则G 为 BF 中点,
D C
即有 BF ? 2FG ,则 AF ?
FB
AF ? 1 .
2FG 2k
【总结】考查三角形一边平行线性质定理的应用,构造“A”“8”叠加的基本图形.
【练习 32】如图,在?ABC 中,AD 是 BC 上的高,且 BC = 5,AD = 3,矩形 EFGH 的顶点
F、G 在边 BC 上,顶点 E、H 分别在边 AB 和 AC 上,如果设边 EF 的长为 x(0 < x < 3),矩形 EFGH 的面积为 y,那么 y 关于 x 的函数解析式是 .
A
E
H
B
F
D G
C
【难度】★★
【答案】 y ? 5x ? 5 x2 .
3
【解析】由 EH / /BC ,EF / / AD ,根据三角形一边平行线的性质, 即得: EF ? BE , EH ? AE ,则有 EF ? EH ? 1 ,
AD AB
BC AB
AD BC
即 x ? EH ? 1 ,得: EH ? 5 ? 5 x , y ? EH ? EF ? 5x ? 5 x2 .
3 5 3 3
【总结】考查三角形一边平行线性质定理的综合应用,进行比例转化解决问题.
1106424-871952【练习 33】已知:在?ABC 中,AC = a,cos C = 4 ,AB 与 BC 所在直线成 45°角,则 AC 边
5
上的高的长是 . A
【难度】★★★
【答案】 21 a 或 3 a .
25 25
【解析】作 AD ? BC 所在直线于点 D ,
B C
D B'
由 AC = a,cos C = 4 ,可得CD ? 4 a ,勾股定理得 AD ? 3 a , AB 与 BC 所在直线成
5 5 5
45°角,由此需进行分类讨论,
B 在 D 点左侧,有?B ? 45? ,可得 BD ? AD ? 3 a ,则 BC ? CD ? BD ? 7 a ,
5
3 a ? 7 a
由面积法可得 AC 边上的高长为 AD ? BC ? 5 5
AC a
5
? 21 a ;
25
B ' 在 D 点右侧,有?B ' ? 45? ,可得 B ' D ? AD ? 3 a ,则 B 'C ? CD ? B ' D ? 1 a ,
5
3 a ? 1 a
由面积法可得 AC 边上的高长为 AD ? BC ? 5 5 ?
AC a
5
3 a .
25
【总结】考查多解性问题,由直线可知题目存在多解,结合锐角三角比和面积法即可求得高长,也可直接利用锐角三角比求高长.
【练习 34】如图所示,在?ABC 中,BC = 6,E、F 分别是 AB、AC 的中点,动点 P 在射线
EF 上,BP 交 CE 于 D, ?CBP 的平分线交 CE 于 Q, A
E P F
D
Q
C
当CQ ? 1 CE 时,EP + BP = .
3
G
【难度】★★★
【答案】12. B
【解析】延长 BQ 交 EF 延长线于点G .
由 E、F 分别是 AB、AC 中点,得 EF 为?ABC 中位线,
则有 EF / /BC ,可得: ?G ? ?GBC ,由?PBQ ? ?CBG ,则有?PBQ ? ?G ,
CE
则有 BP ? PG ,EP ? BP ? EG ,由CQ ? 1 ,则有CQ ? 1 EQ ,则有 BC ? CQ ? 1 ,
3 2
由 BC ? 6 ,则 EG ? 2BC ?12 ,即 EP ? BP ?12 .
EG EQ 2
【总结】考查角平分线与平行线产生等腰三角形的基本图形,构成“8”字型比例转换即可.
【练习 35】已知在?ABC 中, ?ACB ? 60? ,AC = 2,BC = 6,将?ABC 沿着 DE 翻折,使点 B 与点 C 重合,折痕 DE 交 AB 于点 D,交 BC 于点 E,那么?ACD 的面积为 .
A
D
【难度】★★★
【答案】 6 3 .
5
【解析】作 AF ? BC 交 BC 于点 F ,
3
由 AC ? 2 , ?ACB ? 60? ,可得: AF ? AC ? sin ?ACB ? ,C B F E
CF ? AC ? cos?ACB ?1 ,依题意可得 DE 垂直平分 BC ,则有 BE ? CE ? 1 BC ? 3 ,
2
DE ? BE ? 3 ,得: DE ? 3 3 , S
? S ? S
? 1 AF ? BC ? 1 DE ? BC ? 6 3 .
AF BF 5
5 ?ACD
?ABC
?BCD
2 2 5
【总结】考查特殊角的锐角三角比的应用和翻折性质的理解应用.
【练习 36】根据三角形外心的概念,我们可引入如下一个新定义:
定义:到三角形的两个顶点距离相等的点,叫做此三角形的准外心.
根据准外心的定义,探究如下问题:如图,在 Rt?ABC 中,?A ? 90? ,BC = 10,AB = 6,
如果准外心 P 在边 AC 上,那么 PA 的长为 . C
【难度】★★★
【答案】4 或 7 .
4
BC2 ? AB2
P
【解析】根据勾股定理,可得: AC ?
? 8 .
1 A B
(1)点 P 到点 A 和点C 距离相等,则 P 为 AC 中点,此时则有 PA ?
AC ? 4 ;
2
(2)点 P 到点 B 和点C 距离相等,则有 PB ? PC ,设 PA ? x ,则 PC ? 8 ? x ? PB ,
在 Rt?ABP 中用勾股定理,则有 BP2 ? AB2 ? AP2 ,即?8 ? x?2 ? 62 ? x2 ,解得: x ? 7 .
4
故 AP 的长为 4 或 7 .
4
【总结】本题应注意多解问题的存在性,也可采用锐角三角比进行求解.
【练习 37】如图,在?AOB 中,已知?AOB ? 90? ,AO = 3,BO = 6,将?AOB 绕顶点 O 逆时针旋转到?A'OB ' 处,此时线段 A' B ' 与 BO 的交点 E 为 BO 的中点,那么线段 B ' E 的
长度为 .
【难度】★★★
【答案】 9 5 .
5
【解析】作OF ? A' B ' 交 A' B ' 于点 F ,根据勾股定理可得:
A
F
B E O
AB ?
AO2 ? BO2 ? 3 5 ,根据面积法可得: OF ? AO ? BO ? 6 5 ,
2663085-117558AB 5
勾股定理可得:EF ?
? 3 5 ,根据旋转性质tan B ? OA ? 1 ? tan B ' ? OF ,
EO2 ? OF 2
5
由此可得: B ' F ? 12 5 , B ' E ? B ' F ? EF ? 9 5 .
OB 2
B ' F
5 5
【总结】考查旋转性质的综合应用.
【练习38】如图,在直线m 上摆放着三个正三角形:?ABC 、?HFG 、?DCE ,已知 BC ? 1 CE ,
2
F、G 分别是 BC、CE 的中点,FM // AC,GN // DC.设图中三个平行四边形的面积依次是 S1 、 S2 、 S3 ,若 S1 ? S3 ? 10 ,则 S2 ???.
【难度】★★★ D
【答案】4. H
【解析】设CD 与GH 交点为 P , A N
由 AB / /FH / /CD ,可得: S1 ? AM ? CF ? 1 , M P
S2 CP CG 2
即得: S
? 2S ,同理可得 S2 ? 1 ,
2 1
3
B F C G E
S
2
则有 S3 ? 2S2 ? 4S1 ,由 S1 ? S3 ? 10 ,可得: S1 ? 2 ,则 S2 ? 2S1 ? 4 .
【总结】考查平行线分等边三角形也得到等边三角形以及面积等比的转化.
【练习 39】如图,在矩形 ABCD 中,已知 AB = 12,AD = 8,如果将矩形沿直线 l 翻折后点
A 落在边 CD 的中点 E 处,直线 l 分别与边 AB、AD 交于点 M、N,那么 MN = .
【难度】★★★
【答案】
125 .
12
A M D
【解析】连结 ME ,依题意可得 MN 垂直平分 AE ,则有 AM ? ME , N E
设 AM ? x ,则有 ME ? x , AD ? 8 ? x ,
在 Rt?DME 中用勾股定理,则有 DM 2 ? DE2 ? ME2 ,
l B C
即?8 ? x?2 ? 62 ? x2 ,解得: x ? 25 , MN ? AE , ?BAD ? 90? ,易得?DAE ? ?ANM ,
AD2 ? DE2
4
勾股定理得: AE ?
? 10 ,则有sin ?DAE ? DE ? 3 ? sin ?ANM ? AM ,
25
即 4 ? 3 ,得: MN ? 125 .
AE 5 MN
MN 5 12
【总结】考查翻折的性质和锐角三角比的综合应用.
【练习 40】如图,在矩形 ABCD 中,AB = 8,BC = 9,点 P 在 BC 边上,CP = 3,点 Q 为线
段 AP 上的动点,射线 BQ 与矩形 ABCD 的一边交于点 R,且 AP = BR,则 QR ? .
BQ
【难度】★★★
【答案】1 或 4 ?
8
19 .
A R D
AB2 ? BP2
【解析】由 BC = 9,CP = 3,可得 BP ? BC ? CP ? 6 , Q
勾股定理可得: AP ?
? 10 ? BR .
B P C
(1)当射线 BQ 与 AD 交于点 R 时,可得 AR ? BP ? 6 ,由 AD / /BC ,则有 QR ? AR ? 1 ;
BQ BP
(2)射线 BQ 与CD 交于点 R ,延长 AP 交 DC 延长线于点 E ,
D
R
P
C
Q
BR2 ? BC2
A
35057418931勾股定理可得: CR ? ? 19 ,由 AB / /CD ,
则有 BP ? AB ,即 6 ? 8
,得CE ? 4 ,
CP CE 3 CE
由此可得: QR ? RE ? 4 ?
BQ AB 8
19 . B
E
【总结】考查三角形一边平行线性质定理的综合应用,注意题目的多解性.
解答题
【练习 41】(1) 2
tan 30?
? 2sin 60?cos 45? ? 3tan 30?sin 45? .
tan 70? tan 20? ? 4cos30? ? 4cos2 30?
(2) tan2 30? ? 2 tan 30? ?1 ? .
【难度】★★
【答案】(1) 2
? tan 60? ? 3tan 45? ? cot 40? cot 50? ? 8 sin2 60? .
?1 ? tan 60??2
3
3
;(2) 2 ? 4 3 ;(3)1.
3
【解析】(1)原式?
2 ? 2 ? 3 ? 2 ? 3? 3 ? 2 ? 2 3 ;
4305769-1168353 2 2 3 2
3
?
3 ? ?
3
4 3
?
(2)原式? 1 ? tan 30? ? 2cos 30? ?1 ? ?1 ? 3 ? ? ? 2 ? 2 ?1? ? 2 ? 3 ;
? ? ? ?
8 ? 3 ?2
284981174305447289584605521015984605(3)原式? tan 60? ?1 ?
3 ? 3?1 ? 1 ? 3 ? ? 2 ?
? ? 3 ?1?? ?3 ?
3 ??1 ? 1 .
? ?
【总结】考查特殊角锐角三角比的计算,去绝对值注意符号.
A
D
F
E
B
G
C
【练习 42】如图,D、E 是?ABC 边 AB 上的点,F、G 分别是边
AC、BC 上的点,且满足 AD = DE = EB,DF // BC,EG // AC.
(1)求证:FG // AB;
1902106-315242455826-315243544402-315243790535-315244436711-31524(2)设CA ? a , CB ? b ,请用向量a 、b 表示向量GF .
【难度】★★
2636572216923
【答案】(1)略;(2) GF ? 2 ?a ? b?.
【解析】(1)证明:
DF / /BC ,? DF ? AD ? 1 ,即 DF ? 1 BC ,
2344851-113447BC AB 3 3
1410766135354EG / / AC ,? BG ? BE ? 1 ,即 BG ? 1 BC ,
BC AB 3 3
2477566115193?BG ? DF . BG / /DF , ?四边形 BGFD 是平行四边形.
?FG / BD ,即 FG / / AB ;
(2)由(1)可得: BG ? BE ? 1 ,又 FG / / AB ,则有 FG ? CG ? 2 ,
BC AB 3 AB BC 3
170270347092 3 3 3
即得GF ? 2 BA ? 2 ?CA ? CB?? 2 ?a ? b?.
【总结】考查三角形一边平行线性质定理的综合应用,同时考查同向向量的意义和向量的线性运算.
【练习 43】如图, ?ABC 中,AC = BC,F 为底边 AB 上一点, BF ? m (m、n > 0),D 是
AF n
CF 中点,联结 AD 并延长交 BC 于 E.
A
F
D
C
E
G
B
(1)求 BE 的值;
EC
(2)若 BE = 2 EC,求证: CF ? AB .
【难度】★★
【答案】(1)
m ? n n
;(2)略.
【解析】(1)过点 F 作 FG / /DE 交 BC 于点G ,
则有 BG ? BF ? m ,又 D 为 CF 中点,可知 E 为GC 中点,
GE AF n
由此可得: BE ? m ? n ;
CE n
(2)证明:BE = 2 EC,则有 BE ? m ? n ? 2 ,
CE n
由此可得: m ? n ,则有 AF ? FB ,即 F 为 AB 中点.
141076587587AC ? BC ,?CF ? AB .
【总结】考查三角形一边平行线性质定理的综合应用,作平行线构造“A”字型和“8”字型等基本图形进行比例变换即可.
【练习 44】在平行四边形 ABCD 中,点 E 在 BC 边上,点 F 在 BC 边的延长线上,且 BE = CF.
5445658343916(1)求证:四边形 AEFD 是平行四边形;
(2)连接 AF,分别交 DE、CD 于 M、N,若?B??AME
A D
M
N
B
E
C
F
【难度】★★
【答案】略.
【解析】证明 四边形 ABCD 是平行四边形,
291063589978? AD / /BC , AD ? BC , BE ? CF ,
?EF ? EC ? CF ? EC ? BE ? BC ? AD ,
?四边形 AEFD 是平行四边形;
(2)四边形 ABCD 是平行四边形,??B ? ?ADC .
,求证:ND AD ? AN ME .
1410767108434?AME ? ?DMN , ?B ? ?AME , ??ADN ? ?DMN .
?MND
? ?DNA ,??ADN ∽ ?DMN ,? AN ?
AD .
14107656828MD ? ME ,?ND ? AD ? AN ? ME .
DN DM
【总结】考查平行四边形性质和相似的结合应用.
D C
E
O
A
B
【练习 45】如图,梯形 ABCD 中,AB // CD,AD = BC,点 E 在边 AD 上,BE 与 AC 相交于点 O,且?ABE ? ?BCA .
37145375889求证:(1) ?BAE ∽ ?BOA ;(2) BO BE ? BC AE .
【难度】★★
【答案】略.
【解析】证明 四边形 ABCD 是等腰梯形,
??DAB ? ?ABC .
141076789978?ABE ? ?BCA , ?OAB ? ?BAC ,
??AOB ∽ ?ABC .
??AOB ? ?ABC ? ?DAB .
141076890428?ABO ? ?ABE , ? ?BAE ∽ ?BOA ;
(2)由?BAE ∽ ?BOA ,则有 AE ? BE ,
? B E ? A .
OA AB
由?AOB ∽ ?ABC ,则有 OA ? OB ,
AB BC
A E O
5087407135350? BE ? BC ,即证 BO BE ? BC AE .
AE BO
【总结】考查相似三角形的判定,先判定在应用进行等比转换.
【练习 46】如图,在?ABC 中, ?ACB ? 90? ,点 D 在边 AB 上,DE 平分?CDB 交边 BC
C
E
A
D
M
B
于点 E,EM 是线段 BD 的垂直平分线.
(1)求证: CD ? BE ;
BC BD
(2)若 AB = 10,cos B = 4 ,求 CD 的长.
5
【难度】★★
【答案】(1)略;(2)5.
EM
【解析】证明:(1)
是线段 BD 的垂直平分线,
?BE ? DE , ?B ? ?EDB .
141076787580?EDB ? ?CDE ,??CDE ? ?B .
1410767109805?DCE ? ?BCD ,
??CDE ∽ ?CBD ,? CD ? DE ? BE .
BC BD BD
(2)由cos B ? BC ? 4 ,可得: BC ? 8 ,同时cos B ? BM ? 4 ,即得: BE ? BE ? 5 ,
AB 5
BE 5
BD 2BM 8
? CD ? BE ? 5 ,即得CD ? 5 .
BC BD 8
【总结】考查锐角三角比在直角三角形中的综合应用.
【练习 47】如图,在?ABC 中, ?BAC ? 90? ,AD 是 BC 边上的高,点 E 在线段 DC 上,
EF ? AB,EG ? AC,垂足分别为 F,G.求证:(1) EG ? CG ;(2) FD ? DG .
AD CD
A
F
G
B
D E
C
【难度】★★
【答案】略.
1944142126317【解析】(1) EG ? AC , AD 是边 BC 上的高,
??ADC ? ?EGC ? 90? ?C ? ?C ,
??E G C∽
?A D C,
? EG ? CG .
AD CD
1478052153421(2)
?BAC ? 90? , EF ? AB , EG ? AC ,?四边形是 AFEG 矩形,
? AF ? EG .
EG ? CG ,
AD CD
? AF ? AD .
CG CD
1410742153622EG ? AC , AD 是边 BC 上的高,即有?DAC ? ?DAF ? 90?,?DAC ? ?C ? 90? ,
??DAF ? ?C , ??FAD ∽ ?GCD ,
??FDA ? ?GDC ,
? FD ? DG .
? ?F D A ? ?G D A? ? G D C? ? ,即?FDG ? ?ADC ,
【总结】考查相似三角形判定定理 1 与定理 2 和相似三角形性质的综合题,需要根据题目需求进行变形,找准题目所求结论,然后根据性质和判定进行灵活转换.
【练习 48】据新华社 2014 年 12 月 13 日电,参加湄公河联合巡逻执法的中国巡逻船顺利返航.已知在巡逻过程中,某一天上午,我巡逻船正在由西向东匀速行驶,10:00 巡逻船在 A 处发现北偏东 53.1°方向,相距 10 海里的 C 处有一个不明物体正在向正东方向移动,10:15 巡逻船在 B 处又测得该物体位于北偏东 18.4°方向的 D 处.若巡逻船的速度是每小时 36 海里.
(1)试在图中画出点 D 的大致位置,并求不明物体移动的速度;
(2)假设该不明物体移动的方向和速度保持不变,巡逻船航行的方向和速度也不变,试问什么时间该物体与我巡逻船之间的距离最近?
(备用数据:sin 53.1?? 0.8 ,cos53.1?? 0.6 ,cot 53.1?? 0.75 ,sin18.4?? 0.32 ,cos18.4?? 0.95 ,
cot18.4?? 3 )
【难度】★★★
【答案】(1) D 点位置如图,不明物体移动速度为每小时 12 海里;(2)10:20 该物体与巡逻船距离最近.
【解析】(1) B 点北偏东 18.4° 即为 D 点位置,如图所示, ?EBD ? 18.4? ;
作CF ? AB 交 AB 于点 F ,则有CF ? BE ,
则有?ACF ? 53.1? ,由此可得 AF ? AC ? sin ?ACF ?10? 0.8 ? 8 ,
CF ? AC ? cos?ACF ?10? 0.6 ? 6 ? BE ,
C E D
由此可得: DE ?
BE
cot ?EBD
? 6 ? 2 ,
3
A F B
巡逻船速度为每小时 36 海里,可得 AB ? 15 ? 36 ? 9 ,则有 FB ? AB ? AF ?1 ? CE ,
60
则CD ? CE ? ED ? 3 ,不明物体速度为3 ? 15 ? 12 海里/小时;
60
(2)两物体距离最近,巡逻船正好在不明物体的下方,转化为追及问题,可知巡逻船行驶时间为8 ? ?36 ?12? ? 1 h ? 20 min ,即 10:20 时该物体与我巡逻船距离最近.
3
【总结】考查方位角和锐角三角比在实际问题中的应用,把相应的长度转化为直角三角形的边长即可.
【练习 49】如图,在?ABC 中, ?C ? 90? ,AC = 4,BC = 3,O 是 AB 上一点, 且 AO : OB = 2 : 5.
(1)过点 O 作OH ? AC 垂足为点 H,求点 O 到直线 AC 的距离 OH 的长;(图 1)
(2)若 P 是边 AC 上的一个动点,作 PQ ? OP 交线段 BC 于点 Q(不与 B、C 重合)(图 2)
①求证: ?POH ∽ ?QPC ;
②设 AP = x,CQ = y,试求 y 关于 x 的函数解析式,并写出定义域;
③当 AP 为何值时,能使?OPQ 与?CPQ 相似.
C
H
B
O
A
图 1
C
Q
P
H
B
O
A
图 2
【难度】★★★
【答案】(1) 6 ;
7
(2)①略;
② y ? ? 7 x2 ? 6x ? 16 ,
6 3
定义域为 8 ? x ? 4 ;
7
③ 26 或10 或18 .
7 7 7
【解析】(1)由OH ? AC , ?C ? 90? , 可得OH / /BC ,则有 OH ? OA ? 2 ,
由此可得: OH ? 6 ;
16120612141927
BC AB 7
(2)①
?OPQ ? 90? ,??CPQ ? ?OPH ? 90? .
?C ? 90? ,??CPQ ? ?CQP ? 90? .
4088561-164080259948889284??CPQ ? ?OPH . ?C ? ?PHO ? 90? , ? ?POH ∽ ?QPC ;
② ?POH ∽ ?QPC ,则有 PH ? OH ,由 tan A ? BC ? 3 ? OH ,可得: AH ? 8 ,
CQ PC AC 4 AH 7
x ? 8 6
则有 PH ? x ? 8 ,CP ? 4 ? x ,即得 7 ? 7 ,整理得:y ? ? 7 x2 ? 6x ? 16 ? 8 ? x ? 4 ? ;
7 y 4 ? x
6 3 ? 7 ?
? ?
③ ?POH ∽ ?QPC ,则有 OP ? OH ,若?OPQ 与?CPQ 相似,则应有 OH ? PH 或
PQ CP
6 6
6 x ? 8
PC OH
OH ? OH ,即可得: 7 ?
??
7 或 7 ?
?
7 ,分别解得: x ? 18 , 10 , 26 .
PC PH
4 ? x x ? 8
7
4 ? x 6
7
7 7 7
【总结】相似的分类讨论只需要转化为一个三角形中的边的关系即可,分类时要注意变化顺序.
【练习 50】如图,在平面直角坐标系中,点 A、C 分别在 x 轴,y 轴上,四边形 ABCO 为矩
形,AB = 16,点 D 与点 A 关于 y 轴对称, tan ?ACB ? 4 ,点 E、F 分别是线段 AD、
3
AC 上的动点(点 E 不与点 A、D 重合),且?CEF ? ?ACB .
(1)求 AC 的长和点 D 的坐标; y
(2)说明?AEF 与?DCE 相似; B C
(3)当?EFC 为等腰三角形时,求点 E 的坐标.
G
【难度】★★★
F
【答案】(1) AC ? 20 , D ?12,0?;(2)略;
? 14 ?
A O E D x
3
(3) ?8,0? 或? ,0 ? .
? ?
【解析】(1)由 AB = 16, tan ?ACB ? 4 ,可得: BC ?
3
AB
tan ?ACB
? 12 ,勾股定理可得
AB2 ? BC2
AC ?
? 20 ,同时可得: AO ? BC ?12 ,则有 A??12,0? ,点 D 与点 A 关于
y 轴对称,可知 D ?12 ,0? ;
(2) CO ? AD,AO ? OD ,可得: AC ? CD ,则有?CAO ? ?CDO ,又 BC / / AO , 得?CAO ? ?ACB ? ?CEF ,由外角可得?CEA ? ?ECD ? ?CDE ? ?CEF ? ?AEF , 由此可得: ?ECD ? ?AEF ,即证?AEF ∽ ?DCE ;
(3)由(2)可得: ?CEF ? ?CAE ,由?FCE ? ?ACE ,可得?EFC ∽ ?AEC , ?EFC 为等腰三角形,即为?AEC 等腰三角形,由此进行分类讨论:
① AE ? AC 时,则有 AE ? 20 , EO ? 8 ,即得 E 点坐标?8,0? ;
② AE ? CE 时,作 EG ? AC 交 AC 于点G ,则有 AG ? 1 AC ? 10 ,
2
此时 tan ?GAE ? tan ?BCA ? 4 ? GE ,则GE ? 40 ,
勾股定理得: AE ?
3 AG 3
AG2 ? GE2
? 50 ,
3
此时 EO ? 14 ,即得: E 点坐标? 14,0 ? ;
3 ? 3 ?
? ?
③ CE ? AC 时,此时 D 、 E 重合,不符合题意,即不存在; 综上所述,点 E 坐标为?8,0? 或? 14,0 ? .
? 3 ?
? ?
【总结】(2)考查利用“一线三等角”基本模型证相似,(3)中的等腰三角形问题通过转化找到简单易算的三角形进行分类讨论即可.
【练习 51】在平行四边形 ABOC 中, AO ? BO ,且 AO = BO,以 AO、BO 所在直线为坐标轴建立如图所示的平面直角坐标系,已知 B( ?6 ,0),直线 y = 3x + b 过点 C 且与 x轴交于点 D.
(1)求点 D 的坐标;
(2)点 E 为 y 轴正半轴上一点,当?BED ? 45? 时,求直线 EC 的解析式;
(3)在(2)的条件下,设直线 EC 与 x 轴交于点 F,ED 与 AC 交于点 G.点 P 从点 O 出发以每秒 1 个单位的速度沿折线 OF—FE 运动,在运动过程中直线 PA 交 BE 于 H,设运动时间为 t.当以 E、H、A 为顶点的三角形与?EGC 相似时,求 t 的值.
【难度】★★★
【答案】(1) D ?4,0? ;(2) y ? ?x ?12 ; (3)6 或15 2 ? 12 .
2
【解析】(1)由 AC ? BO ? AO ,B( ?6 ,0),可得: C ?6,6? ,直线 y = 3x + b 过点 C,
则有3? 6 ? b ? 6 ,得: b ? ?12 ,
令 y ? 3x ?12 ? 0 ,得: x ? 4 ,即得 D ?4,0? ;
(2)设 E ?0,a? ,过点O 作OM / /BE 交 DE 于点 M ,
B
则有?OMD ? ?BED ? 45? ,
由此可得: ?OME ?135? ? ?BAE ,
y E
A G C M
O D F x
根据外角可知?BAO ? ?ABE ? ?BEA ? 45? , ?BED ? ?BEA ? ?AED ? 45? , 所以?ABE ? ?MEO .
BO2 ? OE2
a2 ? 36
由此 ?BAE ∽ ?EMO ,则有 BE ? AE ,勾股定理可得 BE ? ? ,
OM OD 4 2
OE MO
2 2
a ? 6
a2 ? 36
又 ? ? ? ,可得OM ?
BE
a ? 36 ,代入即为
? 2 ,
a2 ? 36
DB 10 5 5 a
5
整理得: a2 ?10a ? 24 ? 0 ,解得: a ? 12 , a ? ?2 (舍),即得 E ?0,12?,
1 2
由此可设CE : y ? kx ?12 过点C ?6,6?,则有6k ?12 ? 6 ,得: k ? ?1,
由此可知直线 EC 解析式为: y ? ?x ?12 ;
(3)分类讨论:①点 P 在OF 上运动时,由CE : y ? ?x ?12 ,可得: F ?12 ,0?,则有
?OFE ? ?ACE ? ?AEC ? 45? ,由此可得?HEA ? ?GEC , ?EHA 与?EGC 相似, 则应有?EAH ? ?ECG ? 45? ,由此可得?OAP ? ?EAH ? 45? , OP ? OA ? 6 ,
P 点运动时间t ? 6 ?1 ? 6s ;
②点 P 在 EF 上运动时,由CE : y ? ?x ?12 ,可得: F ?12 ,0?,
则有?OFE ? ?ACE ? ?AEC ? 45? ,
同①可得?HEA ? ?GEC , ?EHA 与?EGC 相似,
则应有?EHA ? ?ECG ? 45? ,由?BED ? 45? ,可得: DE ? PH ,
可得:直线 PH 解析式为 y ? 1 x ? 6 ,令 y ? 1 x ? 6 ? ?x ? 12 ,
3 3
解得 x ? 9 ,即 P ? 9 15 ? ,
? , ?
2 ? 2 2 ?
? 9 ?2 ? 15 ?2
?12 ? 2 ? ? ? 2 ?
?
? ? ?
15 2
由此根据勾股定理可得 PF ? ? ,
2
由此可知点 P 运动时间为: ? 2
? 12? ?1 ?
? 15 2
? 15 2
? ?
2
?
?
12? s .
? ? ? ?
【总结】考查由角的转化构造找相似三角形的问题.
同课章节目录
