初中数学沪教版九年级上册-第6讲:二次函数的概念及图像学案-教师版
文档属性
| 名称 | 初中数学沪教版九年级上册-第6讲:二次函数的概念及图像学案-教师版 |

|
|
| 格式 | docx | ||
| 文件大小 | 351.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 00:00:00 | ||
图片预览




文档简介
二次函数的概念及图像
内容分析
二次函数是九年级上学期第三章的内容,包括二次函数的概念及其图像.基本要求是理解二次函数的概念,会用描点法画二次函数的图像,会用二次函数的解析式来表达相应的抛物线,并掌握二次函数 y ? ax2 的图像平移得到二次函数
知识结构
11767181547260
模块一:二次函数的概念
y ? ax2 ? c 、y ? a ?x ? m?2 和 y ? a ?x ? m?2 ? k 的图像的规律.重点是二次函数的图像的特征及画法.
知识精讲
1、二次函数
一般地,解析式形如 y ? ax2 ? bx ? c (其中 a、b、c 是常数,且a ? 0 )的函数叫做二次
函数.
二次函数 y ? ax2 ? bx ? c 的定义域为一切实数.而在具体问题中,函数的定义域根据实际意义来确定.
例题解析
【例 1】下列函数解析式中,一定为二次函数的是( )
A. y ? 3x ?1
C. s ? 2t2 ?1
【难度】★
【答案】C
B. y ? ax2 ? bx ? c
D. y ? x2 ? 1
x
【解析】根据二次函数的定义,形如 y ? ax2 ? bx ? c ?a ? 0?的函数是二次函数,由此可知 A
是一次函数,B 选项不能确定a 是否为 0,不一定是二次函数,C 选项符合二次函数的条件,D 选项中出现分式形式,不是整式,也不是二次函数,故选 C.
【总结】考查二次函数的概念.
【例 2】二次函数 y ? ?3 ? x2 中,二次项系数为 ,一次项系数为 ,常数项为 .
【难度】★
【答案】0, ?1 , ?3 .
【解析】二次函数整理成一般形式即为 y ? ?x2 ? 3 ,可知二次项为?x2 ,系数为?1 ;一次项
不存在,则其系数为 0;常数项为?3 .
【总结】考查二次函数的一般形式与其各项系数的关联.
【例 3】二次函数 y ? 3x2 ? 2x ?1 ,当 x ? ?1时,y = ;当 x = 时,y = 0.
【难度】★
【答案】4; ? 1 或 1.
3
【解析】令 x ? ?1,则 y ? 3? ?? 1 ??2
2? ??1? ?1? 4
;令 y ? 3x 2 ? 2x ?1? 0
,解得:x ?? 1 ,
1 3
x2 ? 1.
【总结】考查二次函数的代值计算.
1106424-878476【例 4】当 m 时,函数 y ? ?m2 ? 4?x2 ? ?m ? 2?x ? 3 是二次函数.
【难度】★★
【答案】m ? ?2 .
【解析】函数是二次函数,则有m2 ? 4 ? 0 ,可得m ? ?2 .
【总结】函数是否为二次函数只需最高次二次项系数不为 0 即可,与一次项和常数项无关.
【例 5】用一根 80 cm 的铁丝,把它弯成一个矩形框,求它的最大面积.请设变量,并列出函数解析式: .
【难度】★★
【答案】设矩形一边长为 xcm ,面积为 Scm2 ,相应函数解析式为 S ? ?x2 ? 40x .
【解析】根据题意可设矩形一边长为 xcm ,面积为 Scm2 ,则由长方形周长公式可知长方形另一边长为?40 ? x?cm ,由此可得矩形面积 S ? x?40 ? x? ? ?x2 ? 40x .
【总结】考查函数解析式的确定,根据长方形面积公式找准等量关系即可.
【例 6】已知二次函数 y ? x2 ? bx ? c ,当 x = 0 时,y = 1;当 x = 2 时, y ? ?1 .求当 x ? ?3
时 y 的值.
【难度】★★
【答案】19.
?c ? 1
?b ? ?3
【解析】x = 0 时,y = 1;x = 2, y ? ?1 ,依题意即可得:?4 ? 2b ? c ? ?1 ,解得:?c ? 1 ,
? ?
即得二次函数解析式为 y ? x2 ? 3x ?1 ,当 x ? ?3时, y ? ??3?2 ? 3? ??3? ?1 ? 19 .
【总结】考查二次函数的求值计算,根据题意转化为方程求出相应系数即可.
【例 7】二次函数 y ? ax2 ? bx ?1( a ? 0 )的图像经过点(1,1),则a ? b ?1 的值是( )
A. ?3
【难度】★★
【答案】D
B. ?1
C. 2 D. 3
【解析】二次函数过点(1,1),由此即得a ? b ?1 ? 1,故a ? b ?1 ? 3 ,选 D.
【总结】考查二次函数上的点与函数求值的关联.
【例 8】如图,在 Rt?ABC 中, ?BAC ? 90? ,AB = AC = 2,D 是 BC 上异于 B、C 的一个动点,过点 D 作?ADE ? 45? ,DE 交 AC 于点 E.设 BD = x,AE = y,求 y 关于 x 的函数关系式,并写出自变量 x 的取值范围.
22683052786113222092278611【难度】★★★
【答案】 y ? 1 x2 ?
2
2x ? 2?0 ? x ? 2 2 ?. A
【解析】由?BAC ? 90? ,AB = AC = 2,可得: ?B ? ?C ? 45? , E
1822789131503BC ? 2 2 ,又?ADE ? 45? ,根据三角形的外角性质可得 B D C
5749814336686?A D C? ? B A D? ? B? ? A D E? ? ,由此可得: ?BAD ? ?EDC ,即可证
?BAD ∽ ?CDE ,则有 BA ? BD ,即 2
? x ,即得: CE ? ? 1 x2 ?
2x ,
CD CE 2 2 ? x
32417531190874021963119087则有 y ? AC ? CE ? 2 ? ? ? 1 x2 ? 2x ? ? 1 x2 ?
?
CE 2
2x ? 2 ,
? 2 ? 2
? ?
2
自变量取值范围为0 ? x ? 2 .
【总结】考查利用“一线三等角”的基本模型构造变量的函数关系.
模块二:特殊二次函数的图像
知识精讲
1、 y ? x2 的图像
在平面直角坐标系 xOy 中,按照下列步骤画二次函数 y ? x2 的图像.
(1) 列表:取自变量 x 的一些值,计算相应的函数值 y,如下表所示:
x
?
-2
?1 1
2
-1
? 1
2
0
1
2
1
1 1
2
2
?
y ? x2
?
4
2 1
4
1
1
4
0
1
4
1
2 1
4
4
?
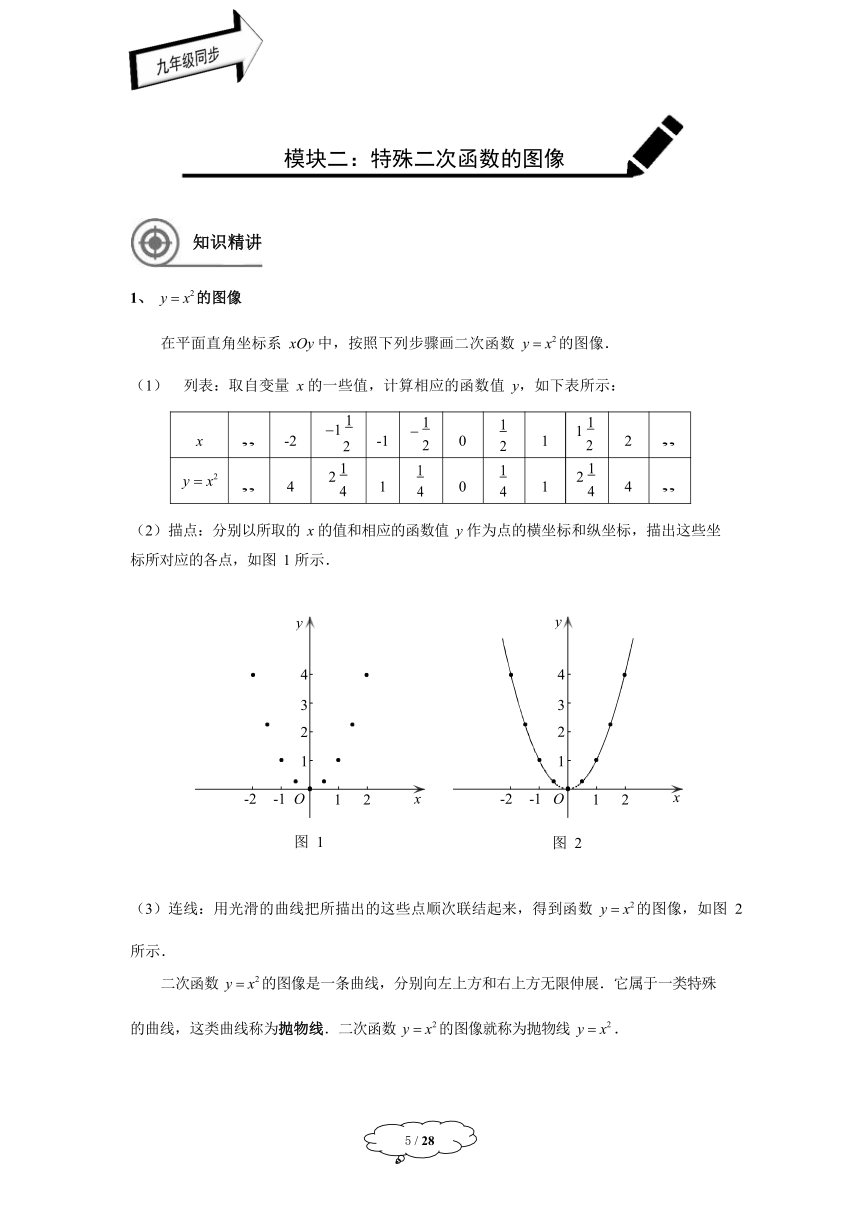
(2)描点:分别以所取的 x 的值和相应的函数值 y 作为点的横坐标和纵坐标,描出这些坐标所对应的各点,如图 1 所示.
y
4
3
2
1
-2 -1 O 1 2
x
y
4
3
2
1
-2 -1 O 1 2
x
图 1
图 2
(3)连线:用光滑的曲线把所描出的这些点顺次联结起来,得到函数 y ? x2 的图像,如图 2
所示.
二次函数 y ? x2 的图像是一条曲线,分别向左上方和右上方无限伸展.它属于一类特殊的曲线,这类曲线称为抛物线.二次函数 y ? x2 的图像就称为抛物线 y ? x2 .
2、二次函数 y ? ax2 的图像
抛物线 y ? ax2 ( a ? 0 )的对称轴是 y 轴,即直线 x = 0;顶点是原点.当a ? 0 时,抛物线开口向上,顶点为最低点;当a ? 0 时,抛物线开口向下,顶点为最高点.
3、二次函数 y ? ax2 ? c 的图像
一般地,二次函数 y ? ax2 ? c 的图像是抛物线,称为抛物线 y ? ax2 ? c ,它可以通过将抛物线 y ? ax2 向上( c ? 0 时)或向下( c ? 0 时)平移 c 个单位得到.
抛物线 y ? ax2 ? c (其中 a、c 是常数,且a ? 0 )的对称轴是 y 轴,即直线 x = 0;顶点坐标
是(0,c).抛物线的开口方向由 a 所取值的符号决定,当a ? 0 时,开口向上,顶点是抛物线的最低点;当a ? 0 时,开口向下,顶点是抛物线的最高点.
4、二次函数 y ? a ?x ? m?2 的图像
一般地,二次函数 y ? a ?x ? m?2 的图像是抛物线,称为抛物线 y ? a ?x ? m?2 ,它可以通过将抛物线 y ? ax2 向左( m ? 0 时)或向右( m ? 0 时)平移 m 个单位得到.
抛物线 y ? a ?x ? m?2 (其中 a、m 是常数,且a ? 0 )的对称轴是过点(-m,0)且平行(或
重合)于 y 轴的直线,即直线 x = -m;顶点坐标是(-m,0).当a ? 0 时,开口向上,顶点是抛物线的最低点;当a ? 0 时,开口向下,顶点是抛物线的最高点.
5、二次函数 y ? a ?x ? m?2 ? k 的图像
二次函数 y ? a? x? m?2
(其中 a 、m 、k 是常数, 且 a ? 0 )的图像即抛物线
y ? a? x? m?2
,可以通过将抛物线 y ? ax2 进行两次平移得到.
这两次平移可以是:先向左( m ? 0 时)或向右( m ? 0 时)平移 m 个单位,再向上( k ? 0
时)或向下( k ? 0 时)平移 k 个单位.
利用图形平移的性质,可知:抛物线 y ? a ?x ? m?2 ? k (其中 a、m、k 是常数,且a ? 0 )的对称轴是经过点( ?m ,0)且平行于 y 轴的直线,即直线 x = ?m ;抛物线的顶点坐标是( ?m ,
k).抛物线的开口方向由 a 所取值的符号决定,当a ? 0 时,开口向上,顶点是抛物线的最低点;当a ? 0 时,开口向下,顶点是抛物线的最高点.
例题解析
【例 9】二次函数 y ?? 1 x2 的图像是 ,开口方向 ,顶点坐标为 .
3
【难度】★
【答案】抛物线,向下, ?0 ,0? .
【解析】二次函数图像是抛物线, a 值决定开口方向, a ? ? 1 ? 0 ,可知开口方向向下,二
3
次函数 y ? ax2 的顶点坐标在坐标原点?0,0? .
【总结】考查形如 y ? ax2 的二次函数图像性质.
【例 10】抛物线 y ? ax2 ? c 的顶点坐标为 ,对称轴为 .
【难度】★
【答案】?0,c?, y 轴.
【解析】二次函数 y ? ax2 ? c 的对称轴为 y 轴,可知其顶点横坐标为 0,则纵坐标为c ,即其顶点坐标为?0,c?.
【总结】考查形如 y ? ax2 ? c 的二次函数对称轴和顶点坐标.
【例 11】抛物线 y ? 2x2 , y ? ?2x2 , y ? 2x2 ?1共有的性质是( )
A.开口向上 B.对称轴都是 y 轴 C.都有最高点 D.顶点都是原点
【难度】★
【答案】B
【解析】二次函数a 值决定其开口方向,有正有负,可知 A、C 错误, y ? 2x2 ?1顶点坐标为?0 ,1? ,可知 D 错误,其对称轴均为 y 轴,B 正确.
【总结】考查形如 y ? ax2 ? c 的二次函数图像特征.
【例 12】抛物线 y ? a ?x ?1?2 有最高点,则 a 的取值范围为 ,最高点的坐标为 .
【难度】★
【答案】a ? 0 , ?1,0? .
【解析】抛物线有最高点,可知开口方向向下,则a ? 0 ,其对称轴为直线 x ? 1,则其顶点即最高点坐标为?1,0? .
【总结】考查形如 y ? a(x ? m)2 (a ? 0) 的二次函数的顶点坐标和开口方向.
【例 13】抛物线 y ? ?2?x ?1?2 ? 3的顶点坐标是( )
A.(1,3) B.(1, ?3 ) C.( ?1 ,3) D.( ?1 , ?3 )
【难度】★
【答案】C
【解析】解析式即为 y ? ?2 ??x ? ??1???2 ? 3 ,可知其顶点坐标为( ?1 ,3),故选 C.
【总结】考查形如 y ? a(x ? m)2 (a ? 0) 的二次函数的顶点坐标.
【例 14】抛物线 y ? ??x ?1?2 上有三点 A( x ,y ),B( x ,y ),C( x ,y ),且?1 ? x
? 0 ,
1 1 2 2 3 3 1
? x2 ? x3 ,则比较 y1 , y2 , y3 的大小为 .
【难度】★★
【答案】 y3 ? y2 ? y1 .
【解析】二次函数对称轴为直线 x ? ?1,且函数开口方向向下,在对称轴右侧 y 值随着 x 的增大而逐渐减小, ?1 ? x1 ? 0 ? x2 ? x3 ,可知 y3 ? y2 ? y1 .
【总结】考查形如 y ? a(x ? m)2 (a ? 0) 的二次函数的增减性与其对称轴和开口方向的关联性.
【例 15】将抛物线 y ? ax2 向左平移后所得新抛物线的顶点横坐标为?2 ,且新抛物线经过点
(1,3),则 a 的值为 .
【难度】★★
1
【答案】 .
3
【解析】向左平移得到新抛物线顶点横坐标为 ?2 ,可知新抛物线解析式为 y ? a ?x ? 2?2 ,
新抛物线过点(1,3),则有?1? 2?2 a ? 3 ,得a ? 1 .
3
【总结】考查二次函数图像的平移和代值计算.
【例 16】将抛物线 y ? 5x2 向左平移 2 个单位,再向下平移 3 个单位,得到的抛物线是( )
A. y ? 5?x ? 2?2 ? 3
C. y ? 5?x ? 2?2 ? 3
B. y ? 5?x ? 2?2 ? 3
D. y ? 5?x ? 2?2 ? 3
【难度】★★
【答案】B
【解析】二次函数图像平移遵循“上加下减,左加右减”的原则,可知答案选 B.
【总结】考查二次函数图像的平移的原则.
【例 17】若直线 y ? 3x ? m 经过第一、三、四象限,则抛物线 y ? ?x ? m?2 ?1的顶点必在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【难度】★★
【答案】B
【解析】 y ? 3x ? m 经过一、三、四象限,可知m ? 0 ,抛物线顶点坐标为?m ,1? ,可知顶点
在第二象限,故选 B.
【总结】考查二次函数的顶点坐标与一次函数经过的象限确定相应参数的正负综合应用.
【例 18】抛物线上有两点(3, ?8 )和( ?5 , ?8 )则它的对称轴是( )
A.直线 x ? ?1
【难度】★★
【答案】A
B.直线 x ? 1
C.直线 x ? 2
D.直线 x ? 3
? ?
【解析】抛物线上有两点(3, ?8 )和( ?5 , ?8 ),纵坐标相同,可知这两点关于抛物线
3 ? ?5
对称轴对称,则对称轴为直线 x ? ? ?1 ,故选 A.
2
【总结】考查二次函数对称轴的求法,两点关于对称轴对称,取其横坐标平均值即可.
【例 19】把抛物线 y ? 2?x ? m?2 向上平移 n 个单位,使新得到的抛物线 y ? ax2 ? bx ? c 通过点(2,5)与(1,1),求 a,b,c,m,n 的值.
【难度】★★★
【答案】a ? 2 , b ? ?2 , c ? 1, m ?? 1 , n ? 1 .
2 2
【解析】抛物线 y ? 2?x ? m?2 向上平移n 个单位,得到新抛物线解析式即为 y ? 2?x ? m?2 ? n ,
? 1
??2?m ? 2?2 ? n ? 5
?m ??
2
抛物线过点(2,5),(1,1),则有?
??2?m ? 1? ? n ? 1
,即可解得: ? 2 ,
1
?n ?
?? 2
? 1 ?2 1
即新抛物线解析式为 y ? 2? x ?
?
? ? ,整理成一般形式即为 y ? 2x2 ? 2x ?1 ,由此即
2
2
?
可得: a ? 2 , b ? ?2 , c ? 1.
【总结】考查二次函数的平移和求值,通过函数上的点转化为解方程得到相应字母的取值即可.
【例 20】如图,抛物线 y ? ax2 上的点 B、C 与 x 轴上的两点 A( ?6 ,0)、D(2,0)构成
平行四边形,BC 与 y 轴相交于点 E(0,6),求系数 a 的值.
y
B
E
C
A
O D
x
【难度】★★★
3
【答案】 .
8
【解析】抛物线 y ? ax2 对称轴为 y 轴,由 BC / / AD ,
可知 BC ?
y 轴, 由此可知 B 、 C 两点关于 y 轴
对称,由 A( ?6 ,0),D(2,0),可知 AD ? 8 .由
四边形 ABCD 为平行四边形,可得: BC ? AD ? 8 .由此可知 B 、C 两点横坐标分别为 ?4 和 4.又 BC 与 y 轴相交于点 E(0,6),可知C ?4 ,6? 在抛物线上,则有42 a ? 6 ,
解得: a ? 3 .
8
【总结】考查根据二次函数上的点确定函数解析式,注意形如 y ? ax2 的二次函数关于 y 轴对称.
模块三:二次函数 y = ax 2+ bx + c 的图像
知识精讲
1、二次函数 y ? ax2 ? bx ? c 的图像
二次函数 y ? ax2 ? bx ? c 的图像称为抛物线 y ? ax2 ? bx ? c ,这个函数的解析式就是这条抛物线的表达式.
任意一个二次函数 y ? ax2 ? bx ? c(其中 a、b、c 是常数,且a ? 0 )都可以运用配方法, 把它的解析式化为 y ? a ?x ? m?2 ? k 的形式.
?
对 y ? ax2 ? bx ? c 配方得: y ? a ? x ?
?
b ?2
?
2a ?
4ac ? b2
?
.
4a
由此可知:
抛物线 y ? ax2 ? bx ? c (其中 a、b、c 是常数,且a ? 0 )的对称轴是直线 x ?? b ,顶
2a
点坐标是( ? b ,
2a
4ac ? b2
).
4a
当 a ? 0 时,抛物线 y ? ax2 ? bx ? c 开口向上,顶点是抛物线的最低点,抛物线在对称
轴(即直线 x ?? b
2a
)左侧的部分是下降的,在对称轴右侧的部分是上升的;
当 a ? 0 时,抛物线 y ? ax2 ? bx ? c 开口向下,顶点是抛物线的最高点,抛物线在对称
轴(即直线 x ?? b
2a
)左侧的部分是上升的,在对称轴右侧的部分是下降的.
2、二次函数 y ? ax2 ? bx ? c 的图像与 x 轴的交点的个数
判断二次函数 y ? ax2 ? bx ? c 的图像与 x 轴交点的个数,即为判断一元二次方程
ax2 ? bx ? c ? 0 的解的个数,这样就可以利用一元二次方程根的判别式? ? b2 ? 4ac 来进行解题.
例题解析
【例 21】说出函数 y ? ?2x2 ? 8x ? 8 的图像的开口方向,对称轴,顶点坐标,这个函数有最
大值还是最小值?是多少?
【难度】★
【答案】函数开口方向向下,对称轴是直线 x ? 2 ,顶点坐标?2,0? ,函数有最大值 0
8
【解析】对函数 y ? ?2x2 ? 8x ? 8 , a ? ?2 , b ? 8 , c ? ?8 , a ? 0 ,可知其开口方向向下,
对称轴为直线 x ? ? b
2a
? ? 2 ? ??2?
? 2 ,顶点坐标即其对称轴与抛物线的交点,横坐标
为 2,纵坐标为?2 ? 22 ? 8? 2 ? 8 ? 0 ,即顶点坐标?2,0? ,函数开口向下,则有最大值,
最大值在顶点处取得,即最大值为 0.
【总结】考查形如 y ? ax2 ? bx ? c ?a ? 0?的二次函数的性质和特征.
【例 22】二次函数 y ? ax2 ? bx ? c 的图像如上右图所示,则abc ,b2 ? 4ac ,2a ? b ,a ? b ? c ,
a ? b ? c 这五个式子中,值为正数的有( )
A.2 个 B.3 个 C.4 个 D.5 个
【难度】★★
y
【答案】
【解析】根据函数图像,函数开口方向向上,可得: a ? 0 ,
对称轴在 0 和 1 之间,即有0 ? ? b
2a
? 1 ,由此可得: b ? 0 ,
O 1
2a ? b ? 0 ,函数与 y 轴交点在 x 轴下方,即得: c ? 0 , x
由此可得: abc ? 0 ,函数与 x 轴有两个交点,即得: b2 ? 4ac ? 0 ;
x ? ?1时, y ? a ? b ? c ? 0 ; x ? 1时, y ? a ? b ? c ? 0 .
综上所述,值为正数的是abc , b2 ? 4ac , 2a ? b , a ? b ? c ,共 4 个,故选 C.
【总结】考查根据二次函数的图像确定二次函数相关特征量.
【例 23】将抛物线 y ? ? 1 x2 ? 3 x ? 6 先向上平移 2 个单位长度,再向右平移 3 个单位长度
6 2
后,得到的抛物线的解析式是 .
【难度】★★
【答案】 y ? ? 1 x2 ? 5 x ? 2 .
6 2
【解析】二次函数 y ? ?
1 x2 ? 3
6 2
x ? 6 整理成顶点式即为 y ? ?
1 ? x ?
6 ?
?
9 ?2
2
?
?
? 75
8
,根据平移“左
1 ? 9 ?2 75
6 2
加右减,上加下减”的原则,平移后所得函数解析式为 y ? ? ? x ? ? 3?
? ?
? ? 2 ,整8
理即为: y ? ? 1 x2 ? 5 x ? 2 .
6 2
【总结】考查二次函数的平移,注意水平方向平移的时候是在对称轴基础上改变 x ,平移遵循“左加右减,上加下减”的原则.
【例 24】已知二次函数 y ? ?x2 ? bx ? 5 ,它的图像经过点(2, ?3 ).
(1)求这个函数关系式及它的图像的顶点坐标;
(2)当 x 为何值时,函数 y 随着 x 的增大而增大?当 x 为何值时,函数 y 随着 x 的增大而减小?
【难度】★★
【答案】(1) y ? ?x2 ? 2x ? 5 ,顶点坐标??1,6? ;(2) x ? ?1 时,函数 y 随着 x 增大而增大; x ? ?1时,函数 y 随着 x 增大而减小.
【解析】(1)函数 y ? ?x2 ? bx ? 5 过点(2, ?3 ),即有?22 ? 2b ? 5 ? ?3 ,得b ? ?2 ,则函
数解析式为 y ? ?x2 ? 2x ? 5 ,化为顶点式即为 y ? ??x ?1?2 ? 6 ,即得顶点坐标??1,6? ;
(2)函数开口方向向下,由此可知,在对称轴左侧,即 x ? ?1 时,函数 y 随着 x 增大而增大;在对称轴右侧,即 x ? ?1时,函数 y 随着 x 增大而减小.
【总结】考查形如 y ? ax2 ? bx ? c ?a ? 0?二次函数的顶点和相应函数的增减性.
【例 25】若直线 y = x + 2 与抛物线 y ? x2 ? 2x 有交点,则它的坐标是 .
【难度】★★
【答案】?1,3? 和??2 ,0? .
【解析】令 x ? 2 ? x2 ? 2x ,整理得: x2 ? x ? 2 ? 0 ,解得: x ? 1 , x ? ?2 ,分别得到对应
1 2
y 值为 3 和 0,即得交点坐标为?1,3? 和??2 ,0? .
【总结】考查二次函数交点坐标,转化为解方程求得对应方程解即为交点横坐标.
【例 26】已知二次函数 y ? x2 ? 2x ? 3,当0 ? x ? 3 时,y 的最大值是 ,最小值是 .
【难度】★★
【答案】0, ?4 .
【解析】函数开口方向向上,对称轴为直线 x ? 1, 0 ? x ? 3 时,函数在顶点处取得最小值,
min
max
x ? 1时, y ? 12 ? 2 ?1? 3 ? ?4 ; x ? 3 距离对称轴较远,即在 x ? 3 时,函数取得最大值 y ? 32 ? 2 ? 3 ? 3 ? 0 .
【总结】考查函数在一定范围内的最值,函数开口方向向上时,在顶点处取得最小值,离顶
点最远的点取得最大值.
y
A
O
B
x
【例 27】已知抛物线 y ? x2 ? 2x ? a 的顶点 A 在直线 y ? ?x ? 3 上,直线 y ? ?x ? 3 与 x 轴的交点为 B 点,点 O 为直角坐标系的原点.
(1)求点 B 的坐标与 a 的值;
(2)求?AOB 的面积.
【难度】★★
【答案】(1) B ?3,0?, a ? 3 ;(2) S?AOB ? 3 .
【解析】(1)令 y ? ?x ? 3 ? 0 ,可得 x ? 3 ,即得 B ?3,0?,二次函
数化为顶点式即为 y ? ?x ?1?2 ? a ?1,顶点坐标?1,a ?1?在直线 y ? ?x ? 3 上,即得?1? 3 ? a ?1,解得: a ? 3 ;
(2)二次函数顶点 A?1,2? ,即得: S
?AOB
? 1 OB ? y
2 A
? 1 ? 3? 2 ? 3 .
2
【总结】考查二次函数的顶点和函数上的点的应用.
【例 28】已知抛物线 y ? x2 ? ?a ? 2? x ? 9 的顶点在坐标轴上,求 a 的值.
【难度】★★★
【答案】a ? 4 或 a ? ?8 或a ? ?2 .
【解析】①函数顶点在 x 轴上时,则有? ? ?a ? 2?2 ? 4 ? 9 ? 0 ,解得: a ? 4 , a ? ?8 ;
1 2
②函数顶点 y 在轴上时,则有a ? 2 ? 0 ,解得: a ? ?2 .
【总结】函数顶点在坐标轴上,未明确说明在横轴还是纵轴,需进行分类讨论,同时注意在坐标轴上时相应与函数中相关数值的关系.
【例 29】若对于任何实数 x,二次函数 y ? ?m ?1?x2 ? 2mx ? m ? 3 的图像全在 x 轴上方,求
m 的取值范围.
【难度】★★★
【答案】m ? 3 .
2
??m ?1 ? 0
?
【解析】函数图像全在 x 轴上方,则应有??? ? ?2m?2 ? 4?m ?1??m ? 3? ? ?8m ? 12 ? 0 ,
解得: m ? 3 .
2
【总结】二次函数图像全部在 x 轴上方或下方即相应的一元二次方程无实数根,同时要关注相应的二次函数开口方向.
【例 30】如图,抛物线 y ? x2 ? 4x 与 x 轴交于 O、A 两点,P 为抛物线上一点,过点 P 的直线 y ? x ? m 与对称轴交于点 Q.
(1)这条抛物线的对称轴是 ,直线 PQ 与 x 轴所夹的锐角的度数是 ;
(2)若两个三角形的面积满足 S
?POQ
? 1 S
3
?PAQ
,求 m 的值;
3365528343918(3)当点 P 在 x 轴下方的抛物线上时,过点 C(2,2)的直线 AC 与直线 PQ 交于点 D, 求:①PD + DQ 的最大值;② PD DQ 的最大值.
【难度】★★★
45262662565【答案】(1)直线 x ? 2 , 45? ;(2)2 或?1 ;(3)① 6 2 ;②18.
1106424-776570y
【解析】(1)根据抛物线的性质,可知抛物线对称轴为
直线 x ? ? b
2a
? ? ?4
2 ?1
? 2 ,直线 y ? x ? m 与 x 轴交点 P
坐标为??m,0? ,与 y 轴交点坐标为?0,m? ,由此可知 F Q
直线与 x 轴所夹锐角为45? ; E
(2)设直线 PQ 交 x 轴于点 B ,分别过点O 、 A 作 PQ 垂线, B O A x
垂足分别是 E 、 F ,则有OE / / AF ,显然当点 B 在
OA 延长线上时,不成立;
①当点 B 在 AO 延长线上时,则有 OE ? S?OPQ ? 1 ,由OE / / AF ,则有 BO ? OE ? 1 ,
AF S?APQ 3
AB AF 3
则 BO ? 1 OA ? 2 ,得: B ??2,0? ,则有?2 ? m ? 0 ,得: m ? 2 ;
2
②当点 B 在线段OA 上时,同理可得OB ? 1 OA ? 1 ,得 B ?1,0? ,则有1? m ? 0 ,得:m ? ?1;
y
,
M C
H
O
D
Q
A
x
P
4
(3)①过点C 作CH / / x 轴交直线 PQ 于点 H , 则?CHQ 为等腰直角三角形,由 C(2,2),
易得?AOC ? 45? ,则有 AC ? PQ ,可得 DQ ? DH , 则有 DP ? DQ ? DP ? DH ? PH ,作 PM ? CH 于点 M
203699274830则有 PH ? 2PM ,易知 PM 最大时, PH 有最大值,
当点 P 在抛物线顶点时有最大值 6,则 PH 最大值为
150239611897431406961189746 2 ,即 DP ? DQ 最大值为6 2 ;
2
②由①可知 DP ? DQ ? 6
,设 DP ? a ,则 DQ ? 6
a ,
2
236391214872933268471482482
则 DP ? DQ ? a ?6 2 ? a?? ??a ? 3 2 ?2 ?18 ,点 P 在抛物线顶点时, a ? 3 ,此时 DP ? DQ 有最大值 18.
【总结】考查二次函数相关的综合应用,注意考虑问题的多解性,最大值注意进行相应的转化然后取得.
随堂检测
2044029335282【习题 1】下列函数中,不是二次函数的是( )
A. y ? 1 ?
2x2
B. y ? 2?x ?1?2 ? 4
C. y ? 1 ?x ?1??x ? 4?
2
D. y ? ?x ? 2?2 ? x2 ?1
【难度】★
【答案】D
【解析】二次函数最高次数必须为 2 次,D 选项整理即为 y ? ?4x ? 5 ,不是二次函数.
【总结】考查对二次函数定义的理解,需化成最简形式后再判断.
【习题 2】抛物线 y ? 2?x ? 3?2 的顶点在( )
A.第一象限 B.第二象限 C.x 轴上 D.y 轴上
【难度】★
【答案】C
【解析】抛物线 y ? 2?x ? 3?2 顶点坐标为?3,0? ,即知函数顶点在 x 轴上.
【总结】考查根据二次函数配方后的式子得到二次函数的顶点坐标.
【习题 3】已知抛物线 y ? x2 ? 4x ? 3 ,请回答以下问题:
(1)它的开口方向 ,对称轴是直线 ,顶点坐标为 ;
(2)图像与 x 轴的交点为 ,与 y 轴的交点为 .
【难度】★
【答案】(1)向上, x ? ?2 , ??2,?1?;(2) ??1,0? 和??3,0? , ?0,3?
【解析】(1) a ? 1 ? 0 ,可知函数开口方向向上,对称轴为直线 x ? ? b
2a
? ? 4
2 ?1
? ?2 ,化
为顶点式即为 y ? ?x ? 2?2 ?1 ,可知函数顶点坐标为??2,?1?;
(2)令 y ? x2 ? 4x ? 3 ? 0 ,解得; x ? ?1 , x ? ?3 ,即得函数图像与 x 轴交点坐标为??1,0?
1 2
和??3,0? ,令 x ? 0 ,可得: y ? 3 ,即得函数与 y 轴交点坐标为?0,3? .
【总结】考查根据二次函数各项系数确定二次函数相关特征量.
【习题 4】有下列 4 个函数关系式:1 正方形的面积 S 与边长 x 的关系; 2 圆的面积 S 与圆周长 l 的关系; 3 已知周长为 l 的矩形中,面积 S 与一边长 x 的关系; 4 已知面积为 S 的矩形中,周长 l 与一边长 x 的关系.其中二次函数有( )
A.1 个 B.2 个 C.3 个 D.4 个
【难度】★★
【答案】C
【解析】根据题目所描述相关数学量之间的关系,可得到相应函数关系式分别为① S ? x2 ;
? l ?2 1
? l ? l
? S ? 2S
2?
② S ? ? ? ? ?
? ?
? 4?
l2 ;③ S ? x ?
? 2
? x ? ? ?x2 ?
?
x ;④ l ? 2? x ?
2 ?
? ? 2x ?
x
?
.根据
x
二次函数的定义,可知①②③是二次函数,④不是整式,即不是二次函数,故选 C.
【总结】考查根据等量关系写出相应函数关系式,同时考查二次函数的判断.
【习题 5】抛物线 y ? ax2 ? bx ? 2 经过点( ?2 ,3),则3b ? 6a ? .
【难度】★★
【答案】? 3 .
2
【解析】函数 y ? ax2 ? bx ? 2 过点( ?2 ,3),则有??2?2 a ? 2b ? 2 ? 3 ,即可得: 2a ? b ? 1 ,
2
则3b ? 6a ? ?3?2a ? b? ? ? 3 .
2
【总结】考查整体思想的应用.
【习题 6】已知函数 y ? ?m ? 2? xm2 ?m ? ?m ?1? x ,(m 为常数).
(1)当 m 为何值时,这个函数是二次函数?
(2)当 m 为何值时,这个函数是一次函数?
【难度】★★
【答案】(1) m ? ?1或m ? 2 ;(2) m ? 1或 m ? 0 或m ? 1 ?
2
5 或 m ? ?2 .
【解析】(1)函数是二次函数,则相应函数未知项最高次数为 2,且二次项系数不为 0,
?m2 ? m ? 2
?
即得: ?m ? 2 ? 0
,解得m ? ?1或 m ? 2 ;
(2)因为函数是一次函数,则相应函数未知项最高次数为 1,且一次项系数不为 0,故存在
?m2 ? m ? 0
?
以下三种情形:① ?m ? 1 ? 0
?m2 ? m ? 1
,解得: m ? 1或m ? 0 ;② ? ,
?m ? 2 ? m ? 1 ? 0
解得: m ? 1 ?
2
5 ;③ m ? 2 ? 0 ,解得: m ? ?2 .
【总结】考查根据函数次数的相关定义确定相应参数的取值范围,注意分类讨论.
【习题 7】把抛物线 y ? ?2?x ? 2?2 向左平移 4 个单位,再向下平移 3 个单位,求平移后抛物线的函数解析式,并指出它的开口方向,顶点坐标和对称轴.
【难度】★★
【答案】 y ? ?2x2 ? 24x ? 75 ,开口方向向下,顶点??6,? 3? ,对称轴是直线 x ? ?6 .
【解析】根据函数的平移法则,可知平移后的函数解析式为 y ? ?2?x ? 2 ? 4?2 ? 3 ,整理成
一般形式即为 y ? ?2x2 ? 24x ? 75 ,?2 ? 0 ,可知函数开口方向向下,顶点坐标??6,? 3? ,对称轴为直线 x ? ?6 .
【总结】考查二次函数图像的平移,“左加右减,上加下减”.
【习题 8】已知抛物线 y ? ax2 ? bx ? 3 的对称轴是直线 x = 1.
(1)求证:2a + b =0;
(2)若关于 x 的方程ax2 ? bx ? 8 ? 0 的一个根为 4,求方程的另一个根.
【难度】★★
【答案】(1)略;(2) ?2
【解析】(1)证明:函数 y ? ax2 ? bx ? 3 对称轴为直线 x ? ? b
2a
? 1,则有 2a + b =0;
(2)对方程ax2 ? bx ? 8 ? 0 ,根据韦达定理可得 x ? x
? ? b ? 2 ,方程有一根为 4,则方程
1 2
a
另一根为?2 .
【总结】考查二次函数对称轴的性质特征,函数上纵坐标相同的两点关于对称轴对称.
【习题 9】如图,已知矩形 ABCD 的宽 CD = 1,点 C 在 y 轴右侧沿抛物线 y ? x2 ? 6x ?10 滑
动,滑动过程中保持 CD // x 轴.当点 D 在 y 轴上时,AB 正好在 x 轴上.
(1)求矩形的长 BC;
(2)当矩形在滑动过程中被 x 轴分成两部分的面积之比为 1 : 4 时,求点 C 的坐标.
3646884361920【难度】★★★
【答案】(1) BC ? 5 ;(2) ?3,1? 或?3 ?
3 ,4?或?3 ?
3 ,4?. y
【解析】(1)点 D 在 y 轴上时,AB 正好在 x 轴上, 可知 AB ? CD ?1,即C 点横纵标为 1,令 x ? 1,
得 y ? 12 ? 6 ?1?10 ? 5 ,即C ?1,5?,得: BC ? 5 ;
D C
(2)矩形在滑动过程中,被 x 轴分得两部分面积比为
: 4 时,进行分类讨论:
①当 x 轴以上部分比 x 轴以下部分为 1 : 4 时, 则点C 纵坐标为 1,令 x2 ? 6x ?10 ? 1,
解得: x1 ? x2 ? 3 ,此时点坐标为?3,1? ;
(A) B
O x
44292043406405343044340640②当 x 轴以下部分比 x 轴以上部分为 1 : 4 时,则点C 纵坐标为 4,令 x2 ? 6x ?10 ? 4 ,
3
3
4001923501051解得: x1 ? 3 ? , x2 ? 3 ? ,即得C 点坐标?3 ?
3 ,4?为或?3 ?
3 ,4?.
3222069187699综上所述,点C 坐标为?3,1? 或?3 ?
3 ,4?或?3 ?
3 ,4?.
【总结】注意本题未明确说明哪部分面积比时,要进行分类讨论.
【习题 10】如图,二次函数 L :y ? ax2 ? 2ax ? a ? 3(a > 0)和二次函数 L :y ? ?a ?x ?1?2 ?1
1 2
(a > 0)的图像的顶点分别为 M、N,与 y 轴分别交于点 E、F.
(1)函数 y ? ax2 ? 2ax ? a ? 3 (a > 0)的最小值为 ;当二次函数 L 、 L 的 y 值同时
1 2
随着 x 的增大而减小时,x 的取值范围是 ;
(2)当 EF = MN,求 a 的值,并判断四边形 ENFM 的形状(直接写出,不必证明);
y
E
N
M F
O A
x
(3)若二次函数 L2 的图像与 x 轴的右交点为 A(m,0),当?AMN 为等腰三角形时,求方程 ?a ?x ?1?2 ?1 ? 0 的解.
【难度】★★★
【答案】(1)3, ?1 ? x ? 1 ;(2)矩形;
7
7
(3) x1 ? ?1? , x2 ? ?1? 或 x1 ? 2 , x2 ? ?4 .
【解析】(1)将函数 y ? ax2 ? 2ax ? a ? 3 整理成顶点式,
1
即为 y ? a ?x ?1?2 ? 3 ,由 a > 0,可知函数在 x ? 1时有最小值 3;对 L 而言,在对称轴
左侧函数随着 x 的增大而减小,即 x ? 1 ,对 L2 而言,在对称轴右函数随着 x 的增大而减小,即 x ? ?1 ,由此可得: ?1 ? x ? 1 ;
(2)根据函数解析式可得: E ?0,a ? 3? , F ?0,? a ?1? , M ?1,3? , N ??1,1? ,根据两点间距
a2 ?1
离公式,可得: EM ?
? FN , EN ?
? FM ,可知四边形 ENFM 是
a2 ? 4a ? 5
平行四边形,由 EF = MN,即可得四边形 ENFM 是矩形;
2790206127678?m ?1?2 ?1
(3)由(2)可得: MN ? 2 2 , NA ? ? m2 ? 2m ? 2 ,
?m ?1?2 ? 32
MA ? ? m2 ? 2m ?10 ,由此进行分类讨论:
m2 ? 2m ? 2
①当 NA ? MN ,即
? 2 ,解得: m1 ? ?1?
7 , m2 ? ?1?
7 ,即方程
2
4767579-2860615650795-2860617
7
?a ?x ?1?2 ?1 ? 0 解为: x ? ?1? , x ? ?1? ;
1 2
m2 ? 2m ?10
356510066716②当 MA ? MN ,即 ? 2 2 ,方程无解;
m2 ? 2m ?10
③当 NA ? MA 时,即
? m2 ? 2m ? 2 ,解得: m ? 2 ,即 A?2,0? ,则函数
左交点为??4,0?,即可得方程?a ?x ?1?2 ?1 ? 0 解为: x ? 2 , x ? ?4 .
1 2
【总结】本题利用二次函数顶点知识结合勾股定理即可求解,注意等腰三角形的分类讨论.
课后作业
【作业 1】对于任意实数 x,二次函数 y ? ax2 的值总是非正数,则 a 的取值范围是( )
A. a ? 0
【难度】★
【答案】B
B. a ? 0
C. a ? 0
D. a ? 0
【解析】对任意实数 x, ax2 总是非负数,则有a ? 0 ,但同时应注意到函数是二次函数,则必有a ? 0 ,即其取值范围为a ? 0 ,故选 B.
【总结】注意二次项系数不能为 0.
【作业 2】抛物线 y ? 2x2 ? 4x ? 3 ,当 x 时,函数值 y 随 x 的增大而减小;当 x
时,函数值 y 随 x 的增大而增大;当 x 时,函数取最 值为 .
【难度】★
【答案】 x ? 1, x ? 1, ? 1,小, ?5 .
【解析】函数 y ? 2x2 ? 4x ? 3 开口方向向上,对称轴为直线 x ? ?
?4 2 ? 2
? 1 ,在对称轴左侧,
min
即 x ? 1 时,y 随 x 的增大而减小;在对称轴右侧,即 x ? 1时,y 随 x 的增大而增大;在顶点处,即 x ? 1时,函数取得最小值 y ? 2 ?12 ? 4 ?1? 3 ? ?5 .
【总结】考查二次函数的增减性,与函数开口方向有关,在对称轴一侧随着增减.
【作业 3】抛物线 y ? ?3x2 ? x ? 4 与坐标轴的交点个数是( )
A.0 B.1 C.2 D.3
【难度】★
【答案】D
【解析】对方程?3x2 ? x ? 4 ? 0 而言, ? ? ??1?2 ? 4 ? ??3?? 4 ? 49 ? 0 ,可知抛物线与 x 轴有
2 个交点;同时抛物线与 y 轴必有 1 个交点,即与坐标轴共 3 个交点,故选 D.
【总结】与坐标轴的交点注意不要漏掉考虑与 y 轴的交点.
【作业 4】给任意实数 n,得到不同的抛物线 y ? x2 ? n ,当 n = 0,1 或?1 时,关于这些抛
物线有以下结论:①开口方向不同;②对称轴不同;③都有最低点;④可以通过一个抛物线平移得到另一个,其中判断正确的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
【难度】★★
【答案】B
【解析】对函数 y ? x2 ? n ,无论 n 取何值,函数始终开口方向向上,对称轴为 y 轴,函数
顶点都为最低点,而且可以通过上下平移得到,可知①②错误,③④正确,故选 B.
【总结】考查形如 y ? ax2 ? c 二次函数性质,其对称轴始终为 y 轴.
【作业 5】已知函数 y ? ?m ?1? xm2 ?1 ? 3x ,当 m 时,它是二次函数.
【难度】★★
【答案】m ? ?1.
?m2 ? 1 ? 2
?
【解析】函数为二次函数,则未知项最高次数为 2,且二次项系数不为 0,则有?m ?1 ? 0 ,
解得: m ? ?1.
【总结】考查二次函数的定义,注意二次项系数不能为 0.
【作业 6】抛物线 y ? 6?x ?1?2 ? 2 可由抛物线 y ? 6x2 ? 2 向___ _平移_ ___个单位得到.
【难度】★★
【答案】左,1.
【解析】根据二次函数“左加右减,上加下减”的平移原则,可知 y ? 6?x ?1?2 ? 2 是由
y ? 6x2 ? 2 向左平移 1 个单位得到的.
【总结】考查二次函数的平移,遵循“左加右减,上加下减”的原则.
【作业 7】二次函数 y ? ?2?x ? m?2 的图像顶点在 轴上,对称轴直线 x = 1,则函数解
析式为 .
【难度】★★
【答案】 x , y ? ?2?x ?1?2 .
【解析】二次函数 y ? ?2?x ? m?2 顶点坐标为??m,0? ,即函数顶点在 x 轴上,函数对称轴为直线 x ? ?m ,可知m ? ?1,则二次函数解析式为 y ? ?2?x ?1?2 .
【总结】考查二次函数的顶点坐标和对称轴的关系.
【作业 8】已知抛物线 y ? ?x ? m?2 ? ?x ? m? ,其中 m 是常数.
(1)求证:不论 m 为何值,该抛物线与 x 轴一定有两个公共点;
(2)若该抛物线的对称轴为直线 x ? 5 .
2
①求该抛物线的函数解析式;
②该抛物线沿 y 轴向上平移多少个单位长度后,得到的抛物线与 x 轴只有一个公共点?
【难度】★★
【答案】(1)略;(2)① y ? x2 ? 5x ? 6 ;② 1 .
4
1
【解析】(1)证明:令 y ? ?x ? m?2 ? ?x ? m? ? 0 ,即?x ? m??x ? m ?1? ? 0 ,可解得:x
? m ,
x2 ? m ?1 ,可知不论 m 为何值,抛物线与 x 轴一定有两公共点?m,0? 和?m ?1,0? ;
5 m ? ?m ? 1? 5
(2)①函数与 x 轴两交点关于对称轴对称,对称轴为直线 x ? ,即可得: ? ,
2 2 2
解得: m ? 2 ,则函数解析式为 y ? ?x ? 2?2 ? ?x ? 2? ,整理即为 y ? x2 ? 5x ? 6 ;
?
②函数 y ? x2 ? 5x ? 6 整理成顶点式即为 y ? ? x ?
?
5 ?2
2
?
?
1 ,根据函数平移法则,抛物线向上
4
1 ? 5 ?2
4 2
平移 个单位得到函数 y ? ? x ? ?
? ?
,与 x 轴只有一个交点.
【总结】考查二次函数性质和相关特征量的基本应用.
【作业 9】如图 1,一次函数 y ? kx ? b 的图像与二次函数 y ? x2 的图像相交于 A、B 两点,
点 A、B 的横坐标分别为 m、n(m < 0,n > 0).
(1)当m ? ?1,n = 4 时,k = ,b = ; 当m ? ?2 ,n = 3 时,k = ,b = .
(2)用含 m、n 的代数式分别表示 k 与 b.
(3)利用(2)的结论,解答下面问题:
如图 2,直线 AB 与 x 轴、y 轴分别交于点 C、D,点 A 关于 y 的对称点为 E,连接 AO、
OE、ED.
① 当 m ? ?3 ,n > 3 时,求
S?ACO
S?四边形AOED
的值(用含 n 的代数式表示)
②当四边形 AOED 为菱形时,m 与 n 满足的关系为 ;当四边形 AOED
为正方形时,m = ,n = .
y
y
B
B
A
D
A
E
m O
n
x
C O
x
【难度】★★★
?
【答案】(1)3,4,1,6;(2) ?k ? m ? n ;(3)① 3
;② n ? ?2m , ?1 ,2
?b ? ?mn
2n ? 6
【解析】(1)当m ? ?1,n = 4 时,两交点都在二次函数 y ? x2 上,可知交点坐标分别为 A??1,1?
?4k ? b ? 16
和 B ?4,16?,同时两点分别在一次函数 y ? kx ? b 上,则有??k ? b ? 1
?
?k ? 3
,解得: ? ;
?b ? 4
当 m ? ?2 ,n = 3 时,两交点都在二次函数 y ? x2 上,可知交点坐标分别为 A??2,4? 和
?
?
B ?3,9?,同时两点分别在一次函数 y ? kx ? b 上,则有??2k ? b ? 4 ,解得: ?k ? 1 ;
?3k ? b ? 9 ?b ? 6
1106424-878472(2)一次函数与抛物线两交点都在二次函数 y ? x2 上,可知交点坐标分别为 A?m,m2 ?和
B ?n,n2 ?,同时两点分别在一次函数 y ? kx ? b 上,则有?
??kn ? b ? n2
,解得:?k ? m ? n ;
??km ? b ? m2
?
?b ? ?mn
(3)由 y ? kx ? b ? ?m ? n?x ? mn ,可得C ? mn ,0? , D?0,? mn? ;
? m ? n ?
? ?
① m ? ?3 时,根据题意即可得到相关点坐标, A??3,9? , C ? ?3n ,0? , D ?0,3n? ,则有
? n ? 3 ?
1 CO ? y
? ?
3n ? 9
S?ACO ? 2 A ? n ? 3 ? 3 ;
S?四边形AOED
2 ? 1 DO ? x
2 A
2 ? 3n ? 3 2n ? 6
②联结 AE ,由四边形 AOED 为菱形,可得 AE 平分 DO ,则 DO
? 2y
A ,即?mn
? m2 2 ,
得: n ? ?2m ;
由四边形 AOED 为正方形,可得 AE ? DO ,即?2m ? ?mn ,解得: n ? 2 , 由 n ? ?2m ,可得: m ? ?1.
【总结】考查二次函数与一次函数综合题,利用待定系数法求相应字母取值范围,同时注意点坐标与长度的相互转化.
【作业 10】如图,两条抛物线的解析式分别是 y1
? ?ax2 ? ax ?1, y
? ax2 ? ax ?1(其中 a
2
为常数,且a ? 0 ).
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当 a ? 1 时,设 y
? ?ax2 ? ax ?1与 x 轴分别交于 M、N 两点(M 在 N 的左边),
2 1
2
y ? ax2 ? ax ?1与 x 轴分别交于 E、F 两点(E 在 F 的左边),观察 M、N、E、F 四点
坐标,请写出一个你所得到的正确的结论,并说明理由;
(3)设上述两条抛物线相交于 A、B 两点,直线 l、l1 、l2 都垂直于 x 轴, l1 、l2 分别经过
A、B 两点,l 在l1 、l2 之间,且 l 与两条抛物线分别交于 C、D 两点,求线段 CD 的最大值.
【难度】★★★
【答案】(1)答案不唯一,合理即可;(2) MN ? EF ;(3)2.
y
【解析】(1)答案不唯一,例:抛物线 y1 开口方向向下,
y 开口方向向上;抛物线 y 对称轴为直线 x ?? 1 , C
2 1 2
y 对称轴为直线 x ? 1 ;抛物线 y 与 y 都与 x 轴 A
2 2 1 2
有两个不同交点等; O x
(2)当 a ? 1 时, y ? ? 1 x2 ? 1 x ? 1,令 y ? 0 , D B
2 1 2 2 1
解得: x1 ? ?2 , x2 ? 1,即得 M ??2,0?, N ?1,0? ;
同时 y ? 1 x2 ? 1 x ?1 ,令 y ? 0 ,解得: x ? 2 , x ? ?1 ,即得: E ??1,0?, F ?2,0? ,
2 2 2 2 1 2
由此可得 MN ? EF ? 3 ,或得到点 M 与点 F 关于y 轴对称,点 N 与点 E 关于y 轴对称;
(3)依题意可得CD ? y ? y
? ??ax2 ? ax ?1?? ?ax2 ? ax ?1?? ?2ax2 ? 2 ,由a ? 0 ,可知当
1 2
x ? 0 时, CD 有最大值 2.
【总结】考查对函数相关特征量的把握和应用.
内容分析
二次函数是九年级上学期第三章的内容,包括二次函数的概念及其图像.基本要求是理解二次函数的概念,会用描点法画二次函数的图像,会用二次函数的解析式来表达相应的抛物线,并掌握二次函数 y ? ax2 的图像平移得到二次函数
知识结构
11767181547260
模块一:二次函数的概念
y ? ax2 ? c 、y ? a ?x ? m?2 和 y ? a ?x ? m?2 ? k 的图像的规律.重点是二次函数的图像的特征及画法.
知识精讲
1、二次函数
一般地,解析式形如 y ? ax2 ? bx ? c (其中 a、b、c 是常数,且a ? 0 )的函数叫做二次
函数.
二次函数 y ? ax2 ? bx ? c 的定义域为一切实数.而在具体问题中,函数的定义域根据实际意义来确定.
例题解析
【例 1】下列函数解析式中,一定为二次函数的是( )
A. y ? 3x ?1
C. s ? 2t2 ?1
【难度】★
【答案】C
B. y ? ax2 ? bx ? c
D. y ? x2 ? 1
x
【解析】根据二次函数的定义,形如 y ? ax2 ? bx ? c ?a ? 0?的函数是二次函数,由此可知 A
是一次函数,B 选项不能确定a 是否为 0,不一定是二次函数,C 选项符合二次函数的条件,D 选项中出现分式形式,不是整式,也不是二次函数,故选 C.
【总结】考查二次函数的概念.
【例 2】二次函数 y ? ?3 ? x2 中,二次项系数为 ,一次项系数为 ,常数项为 .
【难度】★
【答案】0, ?1 , ?3 .
【解析】二次函数整理成一般形式即为 y ? ?x2 ? 3 ,可知二次项为?x2 ,系数为?1 ;一次项
不存在,则其系数为 0;常数项为?3 .
【总结】考查二次函数的一般形式与其各项系数的关联.
【例 3】二次函数 y ? 3x2 ? 2x ?1 ,当 x ? ?1时,y = ;当 x = 时,y = 0.
【难度】★
【答案】4; ? 1 或 1.
3
【解析】令 x ? ?1,则 y ? 3? ?? 1 ??2
2? ??1? ?1? 4
;令 y ? 3x 2 ? 2x ?1? 0
,解得:x ?? 1 ,
1 3
x2 ? 1.
【总结】考查二次函数的代值计算.
1106424-878476【例 4】当 m 时,函数 y ? ?m2 ? 4?x2 ? ?m ? 2?x ? 3 是二次函数.
【难度】★★
【答案】m ? ?2 .
【解析】函数是二次函数,则有m2 ? 4 ? 0 ,可得m ? ?2 .
【总结】函数是否为二次函数只需最高次二次项系数不为 0 即可,与一次项和常数项无关.
【例 5】用一根 80 cm 的铁丝,把它弯成一个矩形框,求它的最大面积.请设变量,并列出函数解析式: .
【难度】★★
【答案】设矩形一边长为 xcm ,面积为 Scm2 ,相应函数解析式为 S ? ?x2 ? 40x .
【解析】根据题意可设矩形一边长为 xcm ,面积为 Scm2 ,则由长方形周长公式可知长方形另一边长为?40 ? x?cm ,由此可得矩形面积 S ? x?40 ? x? ? ?x2 ? 40x .
【总结】考查函数解析式的确定,根据长方形面积公式找准等量关系即可.
【例 6】已知二次函数 y ? x2 ? bx ? c ,当 x = 0 时,y = 1;当 x = 2 时, y ? ?1 .求当 x ? ?3
时 y 的值.
【难度】★★
【答案】19.
?c ? 1
?b ? ?3
【解析】x = 0 时,y = 1;x = 2, y ? ?1 ,依题意即可得:?4 ? 2b ? c ? ?1 ,解得:?c ? 1 ,
? ?
即得二次函数解析式为 y ? x2 ? 3x ?1 ,当 x ? ?3时, y ? ??3?2 ? 3? ??3? ?1 ? 19 .
【总结】考查二次函数的求值计算,根据题意转化为方程求出相应系数即可.
【例 7】二次函数 y ? ax2 ? bx ?1( a ? 0 )的图像经过点(1,1),则a ? b ?1 的值是( )
A. ?3
【难度】★★
【答案】D
B. ?1
C. 2 D. 3
【解析】二次函数过点(1,1),由此即得a ? b ?1 ? 1,故a ? b ?1 ? 3 ,选 D.
【总结】考查二次函数上的点与函数求值的关联.
【例 8】如图,在 Rt?ABC 中, ?BAC ? 90? ,AB = AC = 2,D 是 BC 上异于 B、C 的一个动点,过点 D 作?ADE ? 45? ,DE 交 AC 于点 E.设 BD = x,AE = y,求 y 关于 x 的函数关系式,并写出自变量 x 的取值范围.
22683052786113222092278611【难度】★★★
【答案】 y ? 1 x2 ?
2
2x ? 2?0 ? x ? 2 2 ?. A
【解析】由?BAC ? 90? ,AB = AC = 2,可得: ?B ? ?C ? 45? , E
1822789131503BC ? 2 2 ,又?ADE ? 45? ,根据三角形的外角性质可得 B D C
5749814336686?A D C? ? B A D? ? B? ? A D E? ? ,由此可得: ?BAD ? ?EDC ,即可证
?BAD ∽ ?CDE ,则有 BA ? BD ,即 2
? x ,即得: CE ? ? 1 x2 ?
2x ,
CD CE 2 2 ? x
32417531190874021963119087则有 y ? AC ? CE ? 2 ? ? ? 1 x2 ? 2x ? ? 1 x2 ?
?
CE 2
2x ? 2 ,
? 2 ? 2
? ?
2
自变量取值范围为0 ? x ? 2 .
【总结】考查利用“一线三等角”的基本模型构造变量的函数关系.
模块二:特殊二次函数的图像
知识精讲
1、 y ? x2 的图像
在平面直角坐标系 xOy 中,按照下列步骤画二次函数 y ? x2 的图像.
(1) 列表:取自变量 x 的一些值,计算相应的函数值 y,如下表所示:
x
?
-2
?1 1
2
-1
? 1
2
0
1
2
1
1 1
2
2
?
y ? x2
?
4
2 1
4
1
1
4
0
1
4
1
2 1
4
4
?
(2)描点:分别以所取的 x 的值和相应的函数值 y 作为点的横坐标和纵坐标,描出这些坐标所对应的各点,如图 1 所示.
y
4
3
2
1
-2 -1 O 1 2
x
y
4
3
2
1
-2 -1 O 1 2
x
图 1
图 2
(3)连线:用光滑的曲线把所描出的这些点顺次联结起来,得到函数 y ? x2 的图像,如图 2
所示.
二次函数 y ? x2 的图像是一条曲线,分别向左上方和右上方无限伸展.它属于一类特殊的曲线,这类曲线称为抛物线.二次函数 y ? x2 的图像就称为抛物线 y ? x2 .
2、二次函数 y ? ax2 的图像
抛物线 y ? ax2 ( a ? 0 )的对称轴是 y 轴,即直线 x = 0;顶点是原点.当a ? 0 时,抛物线开口向上,顶点为最低点;当a ? 0 时,抛物线开口向下,顶点为最高点.
3、二次函数 y ? ax2 ? c 的图像
一般地,二次函数 y ? ax2 ? c 的图像是抛物线,称为抛物线 y ? ax2 ? c ,它可以通过将抛物线 y ? ax2 向上( c ? 0 时)或向下( c ? 0 时)平移 c 个单位得到.
抛物线 y ? ax2 ? c (其中 a、c 是常数,且a ? 0 )的对称轴是 y 轴,即直线 x = 0;顶点坐标
是(0,c).抛物线的开口方向由 a 所取值的符号决定,当a ? 0 时,开口向上,顶点是抛物线的最低点;当a ? 0 时,开口向下,顶点是抛物线的最高点.
4、二次函数 y ? a ?x ? m?2 的图像
一般地,二次函数 y ? a ?x ? m?2 的图像是抛物线,称为抛物线 y ? a ?x ? m?2 ,它可以通过将抛物线 y ? ax2 向左( m ? 0 时)或向右( m ? 0 时)平移 m 个单位得到.
抛物线 y ? a ?x ? m?2 (其中 a、m 是常数,且a ? 0 )的对称轴是过点(-m,0)且平行(或
重合)于 y 轴的直线,即直线 x = -m;顶点坐标是(-m,0).当a ? 0 时,开口向上,顶点是抛物线的最低点;当a ? 0 时,开口向下,顶点是抛物线的最高点.
5、二次函数 y ? a ?x ? m?2 ? k 的图像
二次函数 y ? a? x? m?2
(其中 a 、m 、k 是常数, 且 a ? 0 )的图像即抛物线
y ? a? x? m?2
,可以通过将抛物线 y ? ax2 进行两次平移得到.
这两次平移可以是:先向左( m ? 0 时)或向右( m ? 0 时)平移 m 个单位,再向上( k ? 0
时)或向下( k ? 0 时)平移 k 个单位.
利用图形平移的性质,可知:抛物线 y ? a ?x ? m?2 ? k (其中 a、m、k 是常数,且a ? 0 )的对称轴是经过点( ?m ,0)且平行于 y 轴的直线,即直线 x = ?m ;抛物线的顶点坐标是( ?m ,
k).抛物线的开口方向由 a 所取值的符号决定,当a ? 0 时,开口向上,顶点是抛物线的最低点;当a ? 0 时,开口向下,顶点是抛物线的最高点.
例题解析
【例 9】二次函数 y ?? 1 x2 的图像是 ,开口方向 ,顶点坐标为 .
3
【难度】★
【答案】抛物线,向下, ?0 ,0? .
【解析】二次函数图像是抛物线, a 值决定开口方向, a ? ? 1 ? 0 ,可知开口方向向下,二
3
次函数 y ? ax2 的顶点坐标在坐标原点?0,0? .
【总结】考查形如 y ? ax2 的二次函数图像性质.
【例 10】抛物线 y ? ax2 ? c 的顶点坐标为 ,对称轴为 .
【难度】★
【答案】?0,c?, y 轴.
【解析】二次函数 y ? ax2 ? c 的对称轴为 y 轴,可知其顶点横坐标为 0,则纵坐标为c ,即其顶点坐标为?0,c?.
【总结】考查形如 y ? ax2 ? c 的二次函数对称轴和顶点坐标.
【例 11】抛物线 y ? 2x2 , y ? ?2x2 , y ? 2x2 ?1共有的性质是( )
A.开口向上 B.对称轴都是 y 轴 C.都有最高点 D.顶点都是原点
【难度】★
【答案】B
【解析】二次函数a 值决定其开口方向,有正有负,可知 A、C 错误, y ? 2x2 ?1顶点坐标为?0 ,1? ,可知 D 错误,其对称轴均为 y 轴,B 正确.
【总结】考查形如 y ? ax2 ? c 的二次函数图像特征.
【例 12】抛物线 y ? a ?x ?1?2 有最高点,则 a 的取值范围为 ,最高点的坐标为 .
【难度】★
【答案】a ? 0 , ?1,0? .
【解析】抛物线有最高点,可知开口方向向下,则a ? 0 ,其对称轴为直线 x ? 1,则其顶点即最高点坐标为?1,0? .
【总结】考查形如 y ? a(x ? m)2 (a ? 0) 的二次函数的顶点坐标和开口方向.
【例 13】抛物线 y ? ?2?x ?1?2 ? 3的顶点坐标是( )
A.(1,3) B.(1, ?3 ) C.( ?1 ,3) D.( ?1 , ?3 )
【难度】★
【答案】C
【解析】解析式即为 y ? ?2 ??x ? ??1???2 ? 3 ,可知其顶点坐标为( ?1 ,3),故选 C.
【总结】考查形如 y ? a(x ? m)2 (a ? 0) 的二次函数的顶点坐标.
【例 14】抛物线 y ? ??x ?1?2 上有三点 A( x ,y ),B( x ,y ),C( x ,y ),且?1 ? x
? 0 ,
1 1 2 2 3 3 1
? x2 ? x3 ,则比较 y1 , y2 , y3 的大小为 .
【难度】★★
【答案】 y3 ? y2 ? y1 .
【解析】二次函数对称轴为直线 x ? ?1,且函数开口方向向下,在对称轴右侧 y 值随着 x 的增大而逐渐减小, ?1 ? x1 ? 0 ? x2 ? x3 ,可知 y3 ? y2 ? y1 .
【总结】考查形如 y ? a(x ? m)2 (a ? 0) 的二次函数的增减性与其对称轴和开口方向的关联性.
【例 15】将抛物线 y ? ax2 向左平移后所得新抛物线的顶点横坐标为?2 ,且新抛物线经过点
(1,3),则 a 的值为 .
【难度】★★
1
【答案】 .
3
【解析】向左平移得到新抛物线顶点横坐标为 ?2 ,可知新抛物线解析式为 y ? a ?x ? 2?2 ,
新抛物线过点(1,3),则有?1? 2?2 a ? 3 ,得a ? 1 .
3
【总结】考查二次函数图像的平移和代值计算.
【例 16】将抛物线 y ? 5x2 向左平移 2 个单位,再向下平移 3 个单位,得到的抛物线是( )
A. y ? 5?x ? 2?2 ? 3
C. y ? 5?x ? 2?2 ? 3
B. y ? 5?x ? 2?2 ? 3
D. y ? 5?x ? 2?2 ? 3
【难度】★★
【答案】B
【解析】二次函数图像平移遵循“上加下减,左加右减”的原则,可知答案选 B.
【总结】考查二次函数图像的平移的原则.
【例 17】若直线 y ? 3x ? m 经过第一、三、四象限,则抛物线 y ? ?x ? m?2 ?1的顶点必在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【难度】★★
【答案】B
【解析】 y ? 3x ? m 经过一、三、四象限,可知m ? 0 ,抛物线顶点坐标为?m ,1? ,可知顶点
在第二象限,故选 B.
【总结】考查二次函数的顶点坐标与一次函数经过的象限确定相应参数的正负综合应用.
【例 18】抛物线上有两点(3, ?8 )和( ?5 , ?8 )则它的对称轴是( )
A.直线 x ? ?1
【难度】★★
【答案】A
B.直线 x ? 1
C.直线 x ? 2
D.直线 x ? 3
? ?
【解析】抛物线上有两点(3, ?8 )和( ?5 , ?8 ),纵坐标相同,可知这两点关于抛物线
3 ? ?5
对称轴对称,则对称轴为直线 x ? ? ?1 ,故选 A.
2
【总结】考查二次函数对称轴的求法,两点关于对称轴对称,取其横坐标平均值即可.
【例 19】把抛物线 y ? 2?x ? m?2 向上平移 n 个单位,使新得到的抛物线 y ? ax2 ? bx ? c 通过点(2,5)与(1,1),求 a,b,c,m,n 的值.
【难度】★★★
【答案】a ? 2 , b ? ?2 , c ? 1, m ?? 1 , n ? 1 .
2 2
【解析】抛物线 y ? 2?x ? m?2 向上平移n 个单位,得到新抛物线解析式即为 y ? 2?x ? m?2 ? n ,
? 1
??2?m ? 2?2 ? n ? 5
?m ??
2
抛物线过点(2,5),(1,1),则有?
??2?m ? 1? ? n ? 1
,即可解得: ? 2 ,
1
?n ?
?? 2
? 1 ?2 1
即新抛物线解析式为 y ? 2? x ?
?
? ? ,整理成一般形式即为 y ? 2x2 ? 2x ?1 ,由此即
2
2
?
可得: a ? 2 , b ? ?2 , c ? 1.
【总结】考查二次函数的平移和求值,通过函数上的点转化为解方程得到相应字母的取值即可.
【例 20】如图,抛物线 y ? ax2 上的点 B、C 与 x 轴上的两点 A( ?6 ,0)、D(2,0)构成
平行四边形,BC 与 y 轴相交于点 E(0,6),求系数 a 的值.
y
B
E
C
A
O D
x
【难度】★★★
3
【答案】 .
8
【解析】抛物线 y ? ax2 对称轴为 y 轴,由 BC / / AD ,
可知 BC ?
y 轴, 由此可知 B 、 C 两点关于 y 轴
对称,由 A( ?6 ,0),D(2,0),可知 AD ? 8 .由
四边形 ABCD 为平行四边形,可得: BC ? AD ? 8 .由此可知 B 、C 两点横坐标分别为 ?4 和 4.又 BC 与 y 轴相交于点 E(0,6),可知C ?4 ,6? 在抛物线上,则有42 a ? 6 ,
解得: a ? 3 .
8
【总结】考查根据二次函数上的点确定函数解析式,注意形如 y ? ax2 的二次函数关于 y 轴对称.
模块三:二次函数 y = ax 2+ bx + c 的图像
知识精讲
1、二次函数 y ? ax2 ? bx ? c 的图像
二次函数 y ? ax2 ? bx ? c 的图像称为抛物线 y ? ax2 ? bx ? c ,这个函数的解析式就是这条抛物线的表达式.
任意一个二次函数 y ? ax2 ? bx ? c(其中 a、b、c 是常数,且a ? 0 )都可以运用配方法, 把它的解析式化为 y ? a ?x ? m?2 ? k 的形式.
?
对 y ? ax2 ? bx ? c 配方得: y ? a ? x ?
?
b ?2
?
2a ?
4ac ? b2
?
.
4a
由此可知:
抛物线 y ? ax2 ? bx ? c (其中 a、b、c 是常数,且a ? 0 )的对称轴是直线 x ?? b ,顶
2a
点坐标是( ? b ,
2a
4ac ? b2
).
4a
当 a ? 0 时,抛物线 y ? ax2 ? bx ? c 开口向上,顶点是抛物线的最低点,抛物线在对称
轴(即直线 x ?? b
2a
)左侧的部分是下降的,在对称轴右侧的部分是上升的;
当 a ? 0 时,抛物线 y ? ax2 ? bx ? c 开口向下,顶点是抛物线的最高点,抛物线在对称
轴(即直线 x ?? b
2a
)左侧的部分是上升的,在对称轴右侧的部分是下降的.
2、二次函数 y ? ax2 ? bx ? c 的图像与 x 轴的交点的个数
判断二次函数 y ? ax2 ? bx ? c 的图像与 x 轴交点的个数,即为判断一元二次方程
ax2 ? bx ? c ? 0 的解的个数,这样就可以利用一元二次方程根的判别式? ? b2 ? 4ac 来进行解题.
例题解析
【例 21】说出函数 y ? ?2x2 ? 8x ? 8 的图像的开口方向,对称轴,顶点坐标,这个函数有最
大值还是最小值?是多少?
【难度】★
【答案】函数开口方向向下,对称轴是直线 x ? 2 ,顶点坐标?2,0? ,函数有最大值 0
8
【解析】对函数 y ? ?2x2 ? 8x ? 8 , a ? ?2 , b ? 8 , c ? ?8 , a ? 0 ,可知其开口方向向下,
对称轴为直线 x ? ? b
2a
? ? 2 ? ??2?
? 2 ,顶点坐标即其对称轴与抛物线的交点,横坐标
为 2,纵坐标为?2 ? 22 ? 8? 2 ? 8 ? 0 ,即顶点坐标?2,0? ,函数开口向下,则有最大值,
最大值在顶点处取得,即最大值为 0.
【总结】考查形如 y ? ax2 ? bx ? c ?a ? 0?的二次函数的性质和特征.
【例 22】二次函数 y ? ax2 ? bx ? c 的图像如上右图所示,则abc ,b2 ? 4ac ,2a ? b ,a ? b ? c ,
a ? b ? c 这五个式子中,值为正数的有( )
A.2 个 B.3 个 C.4 个 D.5 个
【难度】★★
y
【答案】
【解析】根据函数图像,函数开口方向向上,可得: a ? 0 ,
对称轴在 0 和 1 之间,即有0 ? ? b
2a
? 1 ,由此可得: b ? 0 ,
O 1
2a ? b ? 0 ,函数与 y 轴交点在 x 轴下方,即得: c ? 0 , x
由此可得: abc ? 0 ,函数与 x 轴有两个交点,即得: b2 ? 4ac ? 0 ;
x ? ?1时, y ? a ? b ? c ? 0 ; x ? 1时, y ? a ? b ? c ? 0 .
综上所述,值为正数的是abc , b2 ? 4ac , 2a ? b , a ? b ? c ,共 4 个,故选 C.
【总结】考查根据二次函数的图像确定二次函数相关特征量.
【例 23】将抛物线 y ? ? 1 x2 ? 3 x ? 6 先向上平移 2 个单位长度,再向右平移 3 个单位长度
6 2
后,得到的抛物线的解析式是 .
【难度】★★
【答案】 y ? ? 1 x2 ? 5 x ? 2 .
6 2
【解析】二次函数 y ? ?
1 x2 ? 3
6 2
x ? 6 整理成顶点式即为 y ? ?
1 ? x ?
6 ?
?
9 ?2
2
?
?
? 75
8
,根据平移“左
1 ? 9 ?2 75
6 2
加右减,上加下减”的原则,平移后所得函数解析式为 y ? ? ? x ? ? 3?
? ?
? ? 2 ,整8
理即为: y ? ? 1 x2 ? 5 x ? 2 .
6 2
【总结】考查二次函数的平移,注意水平方向平移的时候是在对称轴基础上改变 x ,平移遵循“左加右减,上加下减”的原则.
【例 24】已知二次函数 y ? ?x2 ? bx ? 5 ,它的图像经过点(2, ?3 ).
(1)求这个函数关系式及它的图像的顶点坐标;
(2)当 x 为何值时,函数 y 随着 x 的增大而增大?当 x 为何值时,函数 y 随着 x 的增大而减小?
【难度】★★
【答案】(1) y ? ?x2 ? 2x ? 5 ,顶点坐标??1,6? ;(2) x ? ?1 时,函数 y 随着 x 增大而增大; x ? ?1时,函数 y 随着 x 增大而减小.
【解析】(1)函数 y ? ?x2 ? bx ? 5 过点(2, ?3 ),即有?22 ? 2b ? 5 ? ?3 ,得b ? ?2 ,则函
数解析式为 y ? ?x2 ? 2x ? 5 ,化为顶点式即为 y ? ??x ?1?2 ? 6 ,即得顶点坐标??1,6? ;
(2)函数开口方向向下,由此可知,在对称轴左侧,即 x ? ?1 时,函数 y 随着 x 增大而增大;在对称轴右侧,即 x ? ?1时,函数 y 随着 x 增大而减小.
【总结】考查形如 y ? ax2 ? bx ? c ?a ? 0?二次函数的顶点和相应函数的增减性.
【例 25】若直线 y = x + 2 与抛物线 y ? x2 ? 2x 有交点,则它的坐标是 .
【难度】★★
【答案】?1,3? 和??2 ,0? .
【解析】令 x ? 2 ? x2 ? 2x ,整理得: x2 ? x ? 2 ? 0 ,解得: x ? 1 , x ? ?2 ,分别得到对应
1 2
y 值为 3 和 0,即得交点坐标为?1,3? 和??2 ,0? .
【总结】考查二次函数交点坐标,转化为解方程求得对应方程解即为交点横坐标.
【例 26】已知二次函数 y ? x2 ? 2x ? 3,当0 ? x ? 3 时,y 的最大值是 ,最小值是 .
【难度】★★
【答案】0, ?4 .
【解析】函数开口方向向上,对称轴为直线 x ? 1, 0 ? x ? 3 时,函数在顶点处取得最小值,
min
max
x ? 1时, y ? 12 ? 2 ?1? 3 ? ?4 ; x ? 3 距离对称轴较远,即在 x ? 3 时,函数取得最大值 y ? 32 ? 2 ? 3 ? 3 ? 0 .
【总结】考查函数在一定范围内的最值,函数开口方向向上时,在顶点处取得最小值,离顶
点最远的点取得最大值.
y
A
O
B
x
【例 27】已知抛物线 y ? x2 ? 2x ? a 的顶点 A 在直线 y ? ?x ? 3 上,直线 y ? ?x ? 3 与 x 轴的交点为 B 点,点 O 为直角坐标系的原点.
(1)求点 B 的坐标与 a 的值;
(2)求?AOB 的面积.
【难度】★★
【答案】(1) B ?3,0?, a ? 3 ;(2) S?AOB ? 3 .
【解析】(1)令 y ? ?x ? 3 ? 0 ,可得 x ? 3 ,即得 B ?3,0?,二次函
数化为顶点式即为 y ? ?x ?1?2 ? a ?1,顶点坐标?1,a ?1?在直线 y ? ?x ? 3 上,即得?1? 3 ? a ?1,解得: a ? 3 ;
(2)二次函数顶点 A?1,2? ,即得: S
?AOB
? 1 OB ? y
2 A
? 1 ? 3? 2 ? 3 .
2
【总结】考查二次函数的顶点和函数上的点的应用.
【例 28】已知抛物线 y ? x2 ? ?a ? 2? x ? 9 的顶点在坐标轴上,求 a 的值.
【难度】★★★
【答案】a ? 4 或 a ? ?8 或a ? ?2 .
【解析】①函数顶点在 x 轴上时,则有? ? ?a ? 2?2 ? 4 ? 9 ? 0 ,解得: a ? 4 , a ? ?8 ;
1 2
②函数顶点 y 在轴上时,则有a ? 2 ? 0 ,解得: a ? ?2 .
【总结】函数顶点在坐标轴上,未明确说明在横轴还是纵轴,需进行分类讨论,同时注意在坐标轴上时相应与函数中相关数值的关系.
【例 29】若对于任何实数 x,二次函数 y ? ?m ?1?x2 ? 2mx ? m ? 3 的图像全在 x 轴上方,求
m 的取值范围.
【难度】★★★
【答案】m ? 3 .
2
??m ?1 ? 0
?
【解析】函数图像全在 x 轴上方,则应有??? ? ?2m?2 ? 4?m ?1??m ? 3? ? ?8m ? 12 ? 0 ,
解得: m ? 3 .
2
【总结】二次函数图像全部在 x 轴上方或下方即相应的一元二次方程无实数根,同时要关注相应的二次函数开口方向.
【例 30】如图,抛物线 y ? x2 ? 4x 与 x 轴交于 O、A 两点,P 为抛物线上一点,过点 P 的直线 y ? x ? m 与对称轴交于点 Q.
(1)这条抛物线的对称轴是 ,直线 PQ 与 x 轴所夹的锐角的度数是 ;
(2)若两个三角形的面积满足 S
?POQ
? 1 S
3
?PAQ
,求 m 的值;
3365528343918(3)当点 P 在 x 轴下方的抛物线上时,过点 C(2,2)的直线 AC 与直线 PQ 交于点 D, 求:①PD + DQ 的最大值;② PD DQ 的最大值.
【难度】★★★
45262662565【答案】(1)直线 x ? 2 , 45? ;(2)2 或?1 ;(3)① 6 2 ;②18.
1106424-776570y
【解析】(1)根据抛物线的性质,可知抛物线对称轴为
直线 x ? ? b
2a
? ? ?4
2 ?1
? 2 ,直线 y ? x ? m 与 x 轴交点 P
坐标为??m,0? ,与 y 轴交点坐标为?0,m? ,由此可知 F Q
直线与 x 轴所夹锐角为45? ; E
(2)设直线 PQ 交 x 轴于点 B ,分别过点O 、 A 作 PQ 垂线, B O A x
垂足分别是 E 、 F ,则有OE / / AF ,显然当点 B 在
OA 延长线上时,不成立;
①当点 B 在 AO 延长线上时,则有 OE ? S?OPQ ? 1 ,由OE / / AF ,则有 BO ? OE ? 1 ,
AF S?APQ 3
AB AF 3
则 BO ? 1 OA ? 2 ,得: B ??2,0? ,则有?2 ? m ? 0 ,得: m ? 2 ;
2
②当点 B 在线段OA 上时,同理可得OB ? 1 OA ? 1 ,得 B ?1,0? ,则有1? m ? 0 ,得:m ? ?1;
y
,
M C
H
O
D
Q
A
x
P
4
(3)①过点C 作CH / / x 轴交直线 PQ 于点 H , 则?CHQ 为等腰直角三角形,由 C(2,2),
易得?AOC ? 45? ,则有 AC ? PQ ,可得 DQ ? DH , 则有 DP ? DQ ? DP ? DH ? PH ,作 PM ? CH 于点 M
203699274830则有 PH ? 2PM ,易知 PM 最大时, PH 有最大值,
当点 P 在抛物线顶点时有最大值 6,则 PH 最大值为
150239611897431406961189746 2 ,即 DP ? DQ 最大值为6 2 ;
2
②由①可知 DP ? DQ ? 6
,设 DP ? a ,则 DQ ? 6
a ,
2
236391214872933268471482482
则 DP ? DQ ? a ?6 2 ? a?? ??a ? 3 2 ?2 ?18 ,点 P 在抛物线顶点时, a ? 3 ,此时 DP ? DQ 有最大值 18.
【总结】考查二次函数相关的综合应用,注意考虑问题的多解性,最大值注意进行相应的转化然后取得.
随堂检测
2044029335282【习题 1】下列函数中,不是二次函数的是( )
A. y ? 1 ?
2x2
B. y ? 2?x ?1?2 ? 4
C. y ? 1 ?x ?1??x ? 4?
2
D. y ? ?x ? 2?2 ? x2 ?1
【难度】★
【答案】D
【解析】二次函数最高次数必须为 2 次,D 选项整理即为 y ? ?4x ? 5 ,不是二次函数.
【总结】考查对二次函数定义的理解,需化成最简形式后再判断.
【习题 2】抛物线 y ? 2?x ? 3?2 的顶点在( )
A.第一象限 B.第二象限 C.x 轴上 D.y 轴上
【难度】★
【答案】C
【解析】抛物线 y ? 2?x ? 3?2 顶点坐标为?3,0? ,即知函数顶点在 x 轴上.
【总结】考查根据二次函数配方后的式子得到二次函数的顶点坐标.
【习题 3】已知抛物线 y ? x2 ? 4x ? 3 ,请回答以下问题:
(1)它的开口方向 ,对称轴是直线 ,顶点坐标为 ;
(2)图像与 x 轴的交点为 ,与 y 轴的交点为 .
【难度】★
【答案】(1)向上, x ? ?2 , ??2,?1?;(2) ??1,0? 和??3,0? , ?0,3?
【解析】(1) a ? 1 ? 0 ,可知函数开口方向向上,对称轴为直线 x ? ? b
2a
? ? 4
2 ?1
? ?2 ,化
为顶点式即为 y ? ?x ? 2?2 ?1 ,可知函数顶点坐标为??2,?1?;
(2)令 y ? x2 ? 4x ? 3 ? 0 ,解得; x ? ?1 , x ? ?3 ,即得函数图像与 x 轴交点坐标为??1,0?
1 2
和??3,0? ,令 x ? 0 ,可得: y ? 3 ,即得函数与 y 轴交点坐标为?0,3? .
【总结】考查根据二次函数各项系数确定二次函数相关特征量.
【习题 4】有下列 4 个函数关系式:1 正方形的面积 S 与边长 x 的关系; 2 圆的面积 S 与圆周长 l 的关系; 3 已知周长为 l 的矩形中,面积 S 与一边长 x 的关系; 4 已知面积为 S 的矩形中,周长 l 与一边长 x 的关系.其中二次函数有( )
A.1 个 B.2 个 C.3 个 D.4 个
【难度】★★
【答案】C
【解析】根据题目所描述相关数学量之间的关系,可得到相应函数关系式分别为① S ? x2 ;
? l ?2 1
? l ? l
? S ? 2S
2?
② S ? ? ? ? ?
? ?
? 4?
l2 ;③ S ? x ?
? 2
? x ? ? ?x2 ?
?
x ;④ l ? 2? x ?
2 ?
? ? 2x ?
x
?
.根据
x
二次函数的定义,可知①②③是二次函数,④不是整式,即不是二次函数,故选 C.
【总结】考查根据等量关系写出相应函数关系式,同时考查二次函数的判断.
【习题 5】抛物线 y ? ax2 ? bx ? 2 经过点( ?2 ,3),则3b ? 6a ? .
【难度】★★
【答案】? 3 .
2
【解析】函数 y ? ax2 ? bx ? 2 过点( ?2 ,3),则有??2?2 a ? 2b ? 2 ? 3 ,即可得: 2a ? b ? 1 ,
2
则3b ? 6a ? ?3?2a ? b? ? ? 3 .
2
【总结】考查整体思想的应用.
【习题 6】已知函数 y ? ?m ? 2? xm2 ?m ? ?m ?1? x ,(m 为常数).
(1)当 m 为何值时,这个函数是二次函数?
(2)当 m 为何值时,这个函数是一次函数?
【难度】★★
【答案】(1) m ? ?1或m ? 2 ;(2) m ? 1或 m ? 0 或m ? 1 ?
2
5 或 m ? ?2 .
【解析】(1)函数是二次函数,则相应函数未知项最高次数为 2,且二次项系数不为 0,
?m2 ? m ? 2
?
即得: ?m ? 2 ? 0
,解得m ? ?1或 m ? 2 ;
(2)因为函数是一次函数,则相应函数未知项最高次数为 1,且一次项系数不为 0,故存在
?m2 ? m ? 0
?
以下三种情形:① ?m ? 1 ? 0
?m2 ? m ? 1
,解得: m ? 1或m ? 0 ;② ? ,
?m ? 2 ? m ? 1 ? 0
解得: m ? 1 ?
2
5 ;③ m ? 2 ? 0 ,解得: m ? ?2 .
【总结】考查根据函数次数的相关定义确定相应参数的取值范围,注意分类讨论.
【习题 7】把抛物线 y ? ?2?x ? 2?2 向左平移 4 个单位,再向下平移 3 个单位,求平移后抛物线的函数解析式,并指出它的开口方向,顶点坐标和对称轴.
【难度】★★
【答案】 y ? ?2x2 ? 24x ? 75 ,开口方向向下,顶点??6,? 3? ,对称轴是直线 x ? ?6 .
【解析】根据函数的平移法则,可知平移后的函数解析式为 y ? ?2?x ? 2 ? 4?2 ? 3 ,整理成
一般形式即为 y ? ?2x2 ? 24x ? 75 ,?2 ? 0 ,可知函数开口方向向下,顶点坐标??6,? 3? ,对称轴为直线 x ? ?6 .
【总结】考查二次函数图像的平移,“左加右减,上加下减”.
【习题 8】已知抛物线 y ? ax2 ? bx ? 3 的对称轴是直线 x = 1.
(1)求证:2a + b =0;
(2)若关于 x 的方程ax2 ? bx ? 8 ? 0 的一个根为 4,求方程的另一个根.
【难度】★★
【答案】(1)略;(2) ?2
【解析】(1)证明:函数 y ? ax2 ? bx ? 3 对称轴为直线 x ? ? b
2a
? 1,则有 2a + b =0;
(2)对方程ax2 ? bx ? 8 ? 0 ,根据韦达定理可得 x ? x
? ? b ? 2 ,方程有一根为 4,则方程
1 2
a
另一根为?2 .
【总结】考查二次函数对称轴的性质特征,函数上纵坐标相同的两点关于对称轴对称.
【习题 9】如图,已知矩形 ABCD 的宽 CD = 1,点 C 在 y 轴右侧沿抛物线 y ? x2 ? 6x ?10 滑
动,滑动过程中保持 CD // x 轴.当点 D 在 y 轴上时,AB 正好在 x 轴上.
(1)求矩形的长 BC;
(2)当矩形在滑动过程中被 x 轴分成两部分的面积之比为 1 : 4 时,求点 C 的坐标.
3646884361920【难度】★★★
【答案】(1) BC ? 5 ;(2) ?3,1? 或?3 ?
3 ,4?或?3 ?
3 ,4?. y
【解析】(1)点 D 在 y 轴上时,AB 正好在 x 轴上, 可知 AB ? CD ?1,即C 点横纵标为 1,令 x ? 1,
得 y ? 12 ? 6 ?1?10 ? 5 ,即C ?1,5?,得: BC ? 5 ;
D C
(2)矩形在滑动过程中,被 x 轴分得两部分面积比为
: 4 时,进行分类讨论:
①当 x 轴以上部分比 x 轴以下部分为 1 : 4 时, 则点C 纵坐标为 1,令 x2 ? 6x ?10 ? 1,
解得: x1 ? x2 ? 3 ,此时点坐标为?3,1? ;
(A) B
O x
44292043406405343044340640②当 x 轴以下部分比 x 轴以上部分为 1 : 4 时,则点C 纵坐标为 4,令 x2 ? 6x ?10 ? 4 ,
3
3
4001923501051解得: x1 ? 3 ? , x2 ? 3 ? ,即得C 点坐标?3 ?
3 ,4?为或?3 ?
3 ,4?.
3222069187699综上所述,点C 坐标为?3,1? 或?3 ?
3 ,4?或?3 ?
3 ,4?.
【总结】注意本题未明确说明哪部分面积比时,要进行分类讨论.
【习题 10】如图,二次函数 L :y ? ax2 ? 2ax ? a ? 3(a > 0)和二次函数 L :y ? ?a ?x ?1?2 ?1
1 2
(a > 0)的图像的顶点分别为 M、N,与 y 轴分别交于点 E、F.
(1)函数 y ? ax2 ? 2ax ? a ? 3 (a > 0)的最小值为 ;当二次函数 L 、 L 的 y 值同时
1 2
随着 x 的增大而减小时,x 的取值范围是 ;
(2)当 EF = MN,求 a 的值,并判断四边形 ENFM 的形状(直接写出,不必证明);
y
E
N
M F
O A
x
(3)若二次函数 L2 的图像与 x 轴的右交点为 A(m,0),当?AMN 为等腰三角形时,求方程 ?a ?x ?1?2 ?1 ? 0 的解.
【难度】★★★
【答案】(1)3, ?1 ? x ? 1 ;(2)矩形;
7
7
(3) x1 ? ?1? , x2 ? ?1? 或 x1 ? 2 , x2 ? ?4 .
【解析】(1)将函数 y ? ax2 ? 2ax ? a ? 3 整理成顶点式,
1
即为 y ? a ?x ?1?2 ? 3 ,由 a > 0,可知函数在 x ? 1时有最小值 3;对 L 而言,在对称轴
左侧函数随着 x 的增大而减小,即 x ? 1 ,对 L2 而言,在对称轴右函数随着 x 的增大而减小,即 x ? ?1 ,由此可得: ?1 ? x ? 1 ;
(2)根据函数解析式可得: E ?0,a ? 3? , F ?0,? a ?1? , M ?1,3? , N ??1,1? ,根据两点间距
a2 ?1
离公式,可得: EM ?
? FN , EN ?
? FM ,可知四边形 ENFM 是
a2 ? 4a ? 5
平行四边形,由 EF = MN,即可得四边形 ENFM 是矩形;
2790206127678?m ?1?2 ?1
(3)由(2)可得: MN ? 2 2 , NA ? ? m2 ? 2m ? 2 ,
?m ?1?2 ? 32
MA ? ? m2 ? 2m ?10 ,由此进行分类讨论:
m2 ? 2m ? 2
①当 NA ? MN ,即
? 2 ,解得: m1 ? ?1?
7 , m2 ? ?1?
7 ,即方程
2
4767579-2860615650795-2860617
7
?a ?x ?1?2 ?1 ? 0 解为: x ? ?1? , x ? ?1? ;
1 2
m2 ? 2m ?10
356510066716②当 MA ? MN ,即 ? 2 2 ,方程无解;
m2 ? 2m ?10
③当 NA ? MA 时,即
? m2 ? 2m ? 2 ,解得: m ? 2 ,即 A?2,0? ,则函数
左交点为??4,0?,即可得方程?a ?x ?1?2 ?1 ? 0 解为: x ? 2 , x ? ?4 .
1 2
【总结】本题利用二次函数顶点知识结合勾股定理即可求解,注意等腰三角形的分类讨论.
课后作业
【作业 1】对于任意实数 x,二次函数 y ? ax2 的值总是非正数,则 a 的取值范围是( )
A. a ? 0
【难度】★
【答案】B
B. a ? 0
C. a ? 0
D. a ? 0
【解析】对任意实数 x, ax2 总是非负数,则有a ? 0 ,但同时应注意到函数是二次函数,则必有a ? 0 ,即其取值范围为a ? 0 ,故选 B.
【总结】注意二次项系数不能为 0.
【作业 2】抛物线 y ? 2x2 ? 4x ? 3 ,当 x 时,函数值 y 随 x 的增大而减小;当 x
时,函数值 y 随 x 的增大而增大;当 x 时,函数取最 值为 .
【难度】★
【答案】 x ? 1, x ? 1, ? 1,小, ?5 .
【解析】函数 y ? 2x2 ? 4x ? 3 开口方向向上,对称轴为直线 x ? ?
?4 2 ? 2
? 1 ,在对称轴左侧,
min
即 x ? 1 时,y 随 x 的增大而减小;在对称轴右侧,即 x ? 1时,y 随 x 的增大而增大;在顶点处,即 x ? 1时,函数取得最小值 y ? 2 ?12 ? 4 ?1? 3 ? ?5 .
【总结】考查二次函数的增减性,与函数开口方向有关,在对称轴一侧随着增减.
【作业 3】抛物线 y ? ?3x2 ? x ? 4 与坐标轴的交点个数是( )
A.0 B.1 C.2 D.3
【难度】★
【答案】D
【解析】对方程?3x2 ? x ? 4 ? 0 而言, ? ? ??1?2 ? 4 ? ??3?? 4 ? 49 ? 0 ,可知抛物线与 x 轴有
2 个交点;同时抛物线与 y 轴必有 1 个交点,即与坐标轴共 3 个交点,故选 D.
【总结】与坐标轴的交点注意不要漏掉考虑与 y 轴的交点.
【作业 4】给任意实数 n,得到不同的抛物线 y ? x2 ? n ,当 n = 0,1 或?1 时,关于这些抛
物线有以下结论:①开口方向不同;②对称轴不同;③都有最低点;④可以通过一个抛物线平移得到另一个,其中判断正确的个数是( )
A.1 个 B.2 个 C.3 个 D.4 个
【难度】★★
【答案】B
【解析】对函数 y ? x2 ? n ,无论 n 取何值,函数始终开口方向向上,对称轴为 y 轴,函数
顶点都为最低点,而且可以通过上下平移得到,可知①②错误,③④正确,故选 B.
【总结】考查形如 y ? ax2 ? c 二次函数性质,其对称轴始终为 y 轴.
【作业 5】已知函数 y ? ?m ?1? xm2 ?1 ? 3x ,当 m 时,它是二次函数.
【难度】★★
【答案】m ? ?1.
?m2 ? 1 ? 2
?
【解析】函数为二次函数,则未知项最高次数为 2,且二次项系数不为 0,则有?m ?1 ? 0 ,
解得: m ? ?1.
【总结】考查二次函数的定义,注意二次项系数不能为 0.
【作业 6】抛物线 y ? 6?x ?1?2 ? 2 可由抛物线 y ? 6x2 ? 2 向___ _平移_ ___个单位得到.
【难度】★★
【答案】左,1.
【解析】根据二次函数“左加右减,上加下减”的平移原则,可知 y ? 6?x ?1?2 ? 2 是由
y ? 6x2 ? 2 向左平移 1 个单位得到的.
【总结】考查二次函数的平移,遵循“左加右减,上加下减”的原则.
【作业 7】二次函数 y ? ?2?x ? m?2 的图像顶点在 轴上,对称轴直线 x = 1,则函数解
析式为 .
【难度】★★
【答案】 x , y ? ?2?x ?1?2 .
【解析】二次函数 y ? ?2?x ? m?2 顶点坐标为??m,0? ,即函数顶点在 x 轴上,函数对称轴为直线 x ? ?m ,可知m ? ?1,则二次函数解析式为 y ? ?2?x ?1?2 .
【总结】考查二次函数的顶点坐标和对称轴的关系.
【作业 8】已知抛物线 y ? ?x ? m?2 ? ?x ? m? ,其中 m 是常数.
(1)求证:不论 m 为何值,该抛物线与 x 轴一定有两个公共点;
(2)若该抛物线的对称轴为直线 x ? 5 .
2
①求该抛物线的函数解析式;
②该抛物线沿 y 轴向上平移多少个单位长度后,得到的抛物线与 x 轴只有一个公共点?
【难度】★★
【答案】(1)略;(2)① y ? x2 ? 5x ? 6 ;② 1 .
4
1
【解析】(1)证明:令 y ? ?x ? m?2 ? ?x ? m? ? 0 ,即?x ? m??x ? m ?1? ? 0 ,可解得:x
? m ,
x2 ? m ?1 ,可知不论 m 为何值,抛物线与 x 轴一定有两公共点?m,0? 和?m ?1,0? ;
5 m ? ?m ? 1? 5
(2)①函数与 x 轴两交点关于对称轴对称,对称轴为直线 x ? ,即可得: ? ,
2 2 2
解得: m ? 2 ,则函数解析式为 y ? ?x ? 2?2 ? ?x ? 2? ,整理即为 y ? x2 ? 5x ? 6 ;
?
②函数 y ? x2 ? 5x ? 6 整理成顶点式即为 y ? ? x ?
?
5 ?2
2
?
?
1 ,根据函数平移法则,抛物线向上
4
1 ? 5 ?2
4 2
平移 个单位得到函数 y ? ? x ? ?
? ?
,与 x 轴只有一个交点.
【总结】考查二次函数性质和相关特征量的基本应用.
【作业 9】如图 1,一次函数 y ? kx ? b 的图像与二次函数 y ? x2 的图像相交于 A、B 两点,
点 A、B 的横坐标分别为 m、n(m < 0,n > 0).
(1)当m ? ?1,n = 4 时,k = ,b = ; 当m ? ?2 ,n = 3 时,k = ,b = .
(2)用含 m、n 的代数式分别表示 k 与 b.
(3)利用(2)的结论,解答下面问题:
如图 2,直线 AB 与 x 轴、y 轴分别交于点 C、D,点 A 关于 y 的对称点为 E,连接 AO、
OE、ED.
① 当 m ? ?3 ,n > 3 时,求
S?ACO
S?四边形AOED
的值(用含 n 的代数式表示)
②当四边形 AOED 为菱形时,m 与 n 满足的关系为 ;当四边形 AOED
为正方形时,m = ,n = .
y
y
B
B
A
D
A
E
m O
n
x
C O
x
【难度】★★★
?
【答案】(1)3,4,1,6;(2) ?k ? m ? n ;(3)① 3
;② n ? ?2m , ?1 ,2
?b ? ?mn
2n ? 6
【解析】(1)当m ? ?1,n = 4 时,两交点都在二次函数 y ? x2 上,可知交点坐标分别为 A??1,1?
?4k ? b ? 16
和 B ?4,16?,同时两点分别在一次函数 y ? kx ? b 上,则有??k ? b ? 1
?
?k ? 3
,解得: ? ;
?b ? 4
当 m ? ?2 ,n = 3 时,两交点都在二次函数 y ? x2 上,可知交点坐标分别为 A??2,4? 和
?
?
B ?3,9?,同时两点分别在一次函数 y ? kx ? b 上,则有??2k ? b ? 4 ,解得: ?k ? 1 ;
?3k ? b ? 9 ?b ? 6
1106424-878472(2)一次函数与抛物线两交点都在二次函数 y ? x2 上,可知交点坐标分别为 A?m,m2 ?和
B ?n,n2 ?,同时两点分别在一次函数 y ? kx ? b 上,则有?
??kn ? b ? n2
,解得:?k ? m ? n ;
??km ? b ? m2
?
?b ? ?mn
(3)由 y ? kx ? b ? ?m ? n?x ? mn ,可得C ? mn ,0? , D?0,? mn? ;
? m ? n ?
? ?
① m ? ?3 时,根据题意即可得到相关点坐标, A??3,9? , C ? ?3n ,0? , D ?0,3n? ,则有
? n ? 3 ?
1 CO ? y
? ?
3n ? 9
S?ACO ? 2 A ? n ? 3 ? 3 ;
S?四边形AOED
2 ? 1 DO ? x
2 A
2 ? 3n ? 3 2n ? 6
②联结 AE ,由四边形 AOED 为菱形,可得 AE 平分 DO ,则 DO
? 2y
A ,即?mn
? m2 2 ,
得: n ? ?2m ;
由四边形 AOED 为正方形,可得 AE ? DO ,即?2m ? ?mn ,解得: n ? 2 , 由 n ? ?2m ,可得: m ? ?1.
【总结】考查二次函数与一次函数综合题,利用待定系数法求相应字母取值范围,同时注意点坐标与长度的相互转化.
【作业 10】如图,两条抛物线的解析式分别是 y1
? ?ax2 ? ax ?1, y
? ax2 ? ax ?1(其中 a
2
为常数,且a ? 0 ).
(1)请写出三条与上述抛物线有关的不同类型的结论;
(2)当 a ? 1 时,设 y
? ?ax2 ? ax ?1与 x 轴分别交于 M、N 两点(M 在 N 的左边),
2 1
2
y ? ax2 ? ax ?1与 x 轴分别交于 E、F 两点(E 在 F 的左边),观察 M、N、E、F 四点
坐标,请写出一个你所得到的正确的结论,并说明理由;
(3)设上述两条抛物线相交于 A、B 两点,直线 l、l1 、l2 都垂直于 x 轴, l1 、l2 分别经过
A、B 两点,l 在l1 、l2 之间,且 l 与两条抛物线分别交于 C、D 两点,求线段 CD 的最大值.
【难度】★★★
【答案】(1)答案不唯一,合理即可;(2) MN ? EF ;(3)2.
y
【解析】(1)答案不唯一,例:抛物线 y1 开口方向向下,
y 开口方向向上;抛物线 y 对称轴为直线 x ?? 1 , C
2 1 2
y 对称轴为直线 x ? 1 ;抛物线 y 与 y 都与 x 轴 A
2 2 1 2
有两个不同交点等; O x
(2)当 a ? 1 时, y ? ? 1 x2 ? 1 x ? 1,令 y ? 0 , D B
2 1 2 2 1
解得: x1 ? ?2 , x2 ? 1,即得 M ??2,0?, N ?1,0? ;
同时 y ? 1 x2 ? 1 x ?1 ,令 y ? 0 ,解得: x ? 2 , x ? ?1 ,即得: E ??1,0?, F ?2,0? ,
2 2 2 2 1 2
由此可得 MN ? EF ? 3 ,或得到点 M 与点 F 关于y 轴对称,点 N 与点 E 关于y 轴对称;
(3)依题意可得CD ? y ? y
? ??ax2 ? ax ?1?? ?ax2 ? ax ?1?? ?2ax2 ? 2 ,由a ? 0 ,可知当
1 2
x ? 0 时, CD 有最大值 2.
【总结】考查对函数相关特征量的把握和应用.
