陕西省安康二中2020-2021学年度上学期高三一轮理科数学复习10月16日周测卷(五)(Word含解析)
文档属性
| 名称 | 陕西省安康二中2020-2021学年度上学期高三一轮理科数学复习10月16日周测卷(五)(Word含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-22 17:19:14 | ||
图片预览




文档简介
安康二中2020—2021学年度高三一轮复习周测卷(五)
理科数学·函数与方程、函数的应用
2020.10.16
一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1.方程的根所在的区间为
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,4)
2.某建材商场国庆期间搞促销活动,规定:顾客购物总金额不超过800元,不享受任何折扣;如果顾客购物总金额超过800元,则超过800元的部分享受一定的折扣优惠,并按下表折扣分别累计计算.
可以享受折扣优惠金额
折扣率
不超过500元的部分
5%
超过500元的部分
10%
若某顾客在此商场获得的折扣金额为50元,则此人购物实际所支付金额为
A.1500元
B.1550元
C.1750元
D.1800元
3.已知函数则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是
A.[0,1)
B.(-∞,1)
C.(-∞,1]∪(2,+∞)
D.(-∞,0]∪(1,+∞)
4.某高校为提升科研能力,计划逐年加大科研经费投入.若该高校2018年全年投入科研经费1300万元,在此基础上,每年投入的科研经费比上一年增长12%,则该高校全年投入的科研经费开始超过2000万元的年份是(参考数据:lg
1.12≈0.05,lg
1.3≈0.11,lg
2≈0.30)
A.2020年
B.2021年
C.2022年
D.2023年
5.已知奇函数f(x)是R上的单调函数,若函数y=f(2x2+1)+f(λ-x)只有一个零点,则实数λ的值是
A.
B.
C.
D.
6.已知函数记g(x)=f(x)-ex-a,若函数g(x)存在三个零点,则实数a的取值范围是
A.
B.(-2e,-e)
C.
D.
7.设方程10x=|lg(-x)|的两个根分别为x1,x2,则
A.x1x2<0
B.x1x2=0
C.x1x2>1
D.0<x1x2<1
8.已知函数f(x)=lg|x-1|,,若两个函数图象的交点分别为P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),则x1+x2+x3+…+xn=
A.8
B.10
C.12
D.14
二、多项选择题(在每小题给出的选项中,有多项符合题目要求.)
9.若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点所在的区间为
A.(-∞,a)
B.(a,b)
C.(b,c)
D.(c,+∞)
10.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x,则函数g(x)=f(x)-x+3的零点为
A.1
B.3
C.
D.
11.已知定义在R上的函数y=f(x)对任意的x都满足f(x+2)=f(x),当-1≤x<1时,
.若函数g(x)=f(x)-loga|x|至少有6个零点,则实数a的取值范围是
A.
B.(5,+∞)
C.
D.[5,7)
12.已知函数则以下结论正确的是
A.f(-3)+f(2019)=-3
B.f(x)在区间[4,5]上是增函数
C.若方程f(x)=kx+1恰有3个实根,则
D.若函数y=f(x)-b在区间(-∞,4)上有6个零点分别为xi(i=1,2,3,4,5,6),则的取值范围是(0,6)
三、填空题
13.声音的等级f(x)(单位:dB)与声音强度x(单位:W/m2)满足.喷气式飞机起飞时,声音的等级约为140
dB;一般说话时,声音的等级约为60
dB.那么喷气式飞机起飞时声音强度约为一般说话时声音强度的________倍.
14.函数的零点个数为________.
15.某企业准备投入适当的广告费对甲产品进行促销宣传,在一年内预计销售量y(单位:万件)与广告费x(单位:万元)之间的函数关系为.已知生产此产品的年固定投入为4万元,每生产1万件此产品仍需再投入30万元,且能全部售完.若每件甲产品售价(单位:元)定为“平均每件甲产品所占生产成本的150%”与“年平均每件甲产品所占广告费的50%”之和,则年利润W=___________(用x表示),当广告费为1万元时,该企业甲产品的年利润为________万元.
16.设函数若对任意实数b,关于x的方程f(x)-b=0总有实数根,则实数a的取值范围是________.
四、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17.已知函数f(x)=x2-(k-2)x+k2+3k+5有两个零点.
(1)若函数的两个零点是-1和-3,求实数k的值;
(2)若函数的两个零点是α和β,求α2+β2的取值范围.
18.噪声污染已经成为影响人们身体健康和生活质量的严重问题.实践证明,声音强度D(分贝)由公式D=alg
I+b(a,b为非零常数)给出,其中I(W/cm2)为声音能量.
(1)当声音强度D1,D2,D3满足D1+2D2=3D3时,求对应的声音能量I1,I2,I3满足的等量关系式.
(2)当人们低声说话,声音能量为10-13
W/cm2时,声音强度为30分贝;当人们正常说话,声音能量为10-12
W/cm2时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪?
19.“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v(单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.当x不超过4尾/立方米时,v的值为2(千克/年);当4≤x≤20时,v是x的一次函数;当x达到20尾/立方米时,因缺氧等原因,v的值为0(千克/年).
(1)当0<x≤20时,求函数v(x)的解析式.
(2)当养殖密度x为多大时,鱼的年生长量(单位:千克/立方米)f(x)=x·v(x)可以达到最大?并求出最大值.
20.对于函数f(x),若在定义域内存在实数x0,满足f(-x0)=-f(x0),则称f(x)为“M类函数”.
(1)设f(x)=2x+m是定义在区间[-1,1]上的“M类函数”,求实数m的最小值;
(2)若函数为其定义域上的“M类函数”,求实数m的取值范围.
21.已知函数.
(1)若对任意实数m,关于x的方程f(x)=m总有实数解,求a的取值范围;
(2)若a=2,求使得关于x的方程f(x)=kx有三个实数解的实数k的取值范围.
22.已知函数f(x)=2x,g(x)=log2x.
(1)若x0是方程的根,证明:是方程的根.
(2)设方程,的根分别是x1,x2,求x1+x2的值.
安康中学2020—2021学年度高三一轮复习周测卷(五)
理科数学·函数与方程、函数的应用
2020.10.16
参考答案
一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【解析】令,由,,,所以f(1)·f(2)<0,又函数f(x)单调递增,所以f(x)的零点所在的区间为(1,2),故方程
的根所在区间为(1,2).故选B.
2.【解析】设此商场购物总金额为x元,可以获得的折扣金额为y元,由题设可知,
因为y=50>25,所以x>1300,所以0.1×(x-1300)+25=50,解得x=1550,故此人购物实际所支付金额为1550-50=1500(元).故选A.
3.【解析】函数g(x)=f(x)+x-m有零点等价于方程f(x)+x=m有实根,令
画出函数h(x)的大致图象(图略).观察它与直线y=m的交点,得知当m≤0或m>1时,有交点,即函数g(x)=f(x)+x-m有零点.故选D.
4.【解析】若2019年是第1年,则第n年全年投入的科研经费为1300×1.12n万元,由1300×1.12n>2000可得1.3×1.12n>2,所以lg
1.3+nlg
1.12>lg
2,所以n×0.05>0.19,得n>3.8,则正整数n的最小值为4,所以第4年,即2022年全年投入的科研经费开始超过2000万元.故选C.
5.【解析】因为函数y=f(2x2+1)+f(λ-x)只有一个零点,所以方程f(2x2+1)+f(λ-x)=0只有一个实数根.又奇函数f(x)是定义在R上的单调函数,则f(2x2+1)=-f(λ-x)等价于f(2x2+1)=f(x-λ),则2x2+1=x-λ,所以方程2x2-x+1+λ=0只有一个实数根,所以Δ=(-1)2-4×2×(1+λ)=0,解得.故选D.
6.【解析】由题意知函数y=f(x)与y=ex+a的图象有三个交点,作出函数y=f(x)的图象如图所示,当直线y=ex+a经过点时,;当直线y=ex+a经过点B(1,0)时,a=-e.因为函数y=f(x)与y=ex+a的图象有三个交点,所以.故选A.
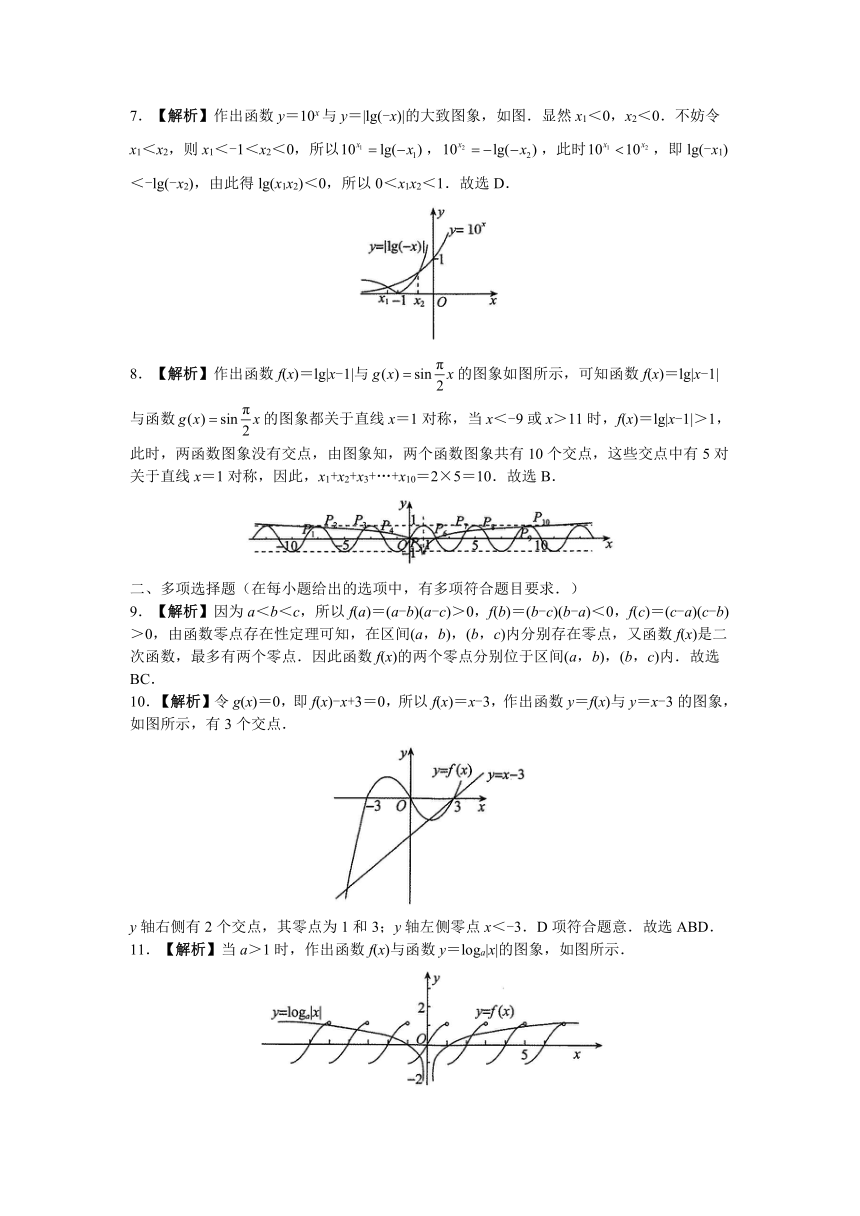
7.【解析】作出函数y=10x与y=|lg(-x)|的大致图象,如图.显然x1<0,x2<0.不妨令x1<x2,则x1<-1<x2<0,所以,,此时,即lg(-x1)<-lg(-x2),由此得lg(x1x2)<0,所以0<x1x2<1.故选D.
8.【解析】作出函数f(x)=lg|x-1|与的图象如图所示,可知函数f(x)=lg|x-1|与函数的图象都关于直线x=1对称,当x<-9或x>11时,f(x)=lg|x-1|>1,此时,两函数图象没有交点,由图象知,两个函数图象共有10个交点,这些交点中有5对关于直线x=1对称,因此,x1+x2+x3+…+x10=2×5=10.故选B.
二、多项选择题(在每小题给出的选项中,有多项符合题目要求.)
9.【解析】因为a<b<c,所以f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0,由函数零点存在性定理可知,在区间(a,b),(b,c)内分别存在零点,又函数f(x)是二次函数,最多有两个零点.因此函数f(x)的两个零点分别位于区间(a,b),(b,c)内.故选BC.
10.【解析】令g(x)=0,即f(x)-x+3=0,所以f(x)=x-3,作出函数y=f(x)与y=x-3的图象,如图所示,有3个交点.
y轴右侧有2个交点,其零点为1和3;y轴左侧零点x<-3.D项符合题意.故选ABD.
11.【解析】当a>1时,作出函数f(x)与函数y=loga|x|的图象,如图所示.
结合图象可知,解得a>5;当0<a<1时,作出函数f(x)与函数y=loga|x|的图象,如图所示.
结合图象可知,解得.故选AB.
12.【解析】函数f(x)的图象如图所示,f(-3)=-9+6=-3,f(2019)=f(1)=f(-1)=1,所以f(-3)+f(2019)=-2,故A错误;由图象可知f(x)在区间[4,5]上是增函数,故B正确;由图象可知当时,直线f(x)=kx+1与函数图象恰有3个交点,故C正确;由图象可得,当函数y=f(x)-b在区间(-∞,4)上有6个零点分别为xi(i=1,2,3,4,5,6)时,则0<b<1,所以当b趋近于0时,趋近于0;当b趋近于1时,趋近于6,所以的取值范围是(0,6),故D正确.故选BCD.
三、填空题
13.108
【解析】设喷气式飞机起飞时声音强度和一般说话时声音强度分别为x1,x2,由题意可得,解得x1=102;,解得x2=10-6,所以.因此喷气式飞机起飞时声音强度约为一般说话时声音强度的108倍.
14.2
【解析】令f(x)=0,得,显然x=-2不是该方程的根,故
,在同一直角坐标系中分别作出函数,的图象如图所示,可知,它们有2个交点,即函数有2个零点.
15.
31.5
【解析】由题意可得产品的生产成本为(30y+4)万元,销售单价为,故年销售收入为
.所以年利润(万元).所以当广告费为1万元,即x=1时,该企业甲产品的年利润为(万元).
16.[0,1]
【解析】若对任意实数b,关于x的方程f(x)-b=0总有实数根,即对任意实数b,函数f(x)的图象与直线y=b总有交点,即函数f(x)的值域为R,因为在同一坐标系中画出函数y=x与y=x2的图象,如图所示,由图可得:当a∈[0,1]时,函数f(x)的值域为R,故实数a的取值范围是[0,1].
四、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17.解:(1)由于-1和-3是函数f(x)的两个零点,
故-1和-3是方程x2-(k-2)x+k2+3k+5=0的两个实数根,
则解得k=-2.
(2)若函数的两个零点为α和β,则α和β是方程x2-(k-2)x+k2+3k+5=0的两根,
所以
则,且α2+β2=(α+β)2-2αβ=-k2-10k-6在区间上单调递减,
所以α2+β2在区间上的最大值是18,最小值是,所以α2+β2的取值范围是.
18.解:(1)因为D1+2D2=3D3,
所以alg
I1+b+2(alg
I2+b)=3(alg
I3+b),
所以lg
I1+2lg
I2=3lg
I3,所以.
(2)由题意得解得
所以100<10lg
I+160<120,解得10-6<I<10-4.
所以,当声音能量I∈(10-6,10-4)时,人会暂时性失聪.
19.解:(1)由题意可知,当0<x≤4时,v(x)=2;
当4≤x≤20时,设v(x)=ax+b(a≠0),
显然v(x)=ax+b在区间[4,20]上是减函数,
则解得
故函数
(2)依题意并由(1)可得,
当0<x≤4时,f(x)为增函数,
故f(x)max=f(4)=8;
当4<x≤20时,,
故f(x)max=f(10)=12.5.
所以当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为12.5千克/立方米.
20.解:(1)因为函数f(x)=2x+m是定义在区间[-1,1]上的“M类函数”,
所以存在实数x0∈[-1,1],满足f(-x0)=-f(x0),
即方程2x+2-x+2m=0在区间[-1,1]上有解.
令t=2x,,则.
令,因为函数g(t)在区间上单调递增,在区间[1,2]上单调递减,
所以当或t=2时,m取得最小值.
(2)由x2-2mx>0对?x≥2恒成立,得m<1.
因为若函数为其定义域上的“M类函数”,
所以存在实数x0,满足f(-x0)=-f(x0),
①当x0≥2时,-x0≤-2,
所以,所以.
因为函数是增函数,所以m≥-1.
②当-2<x0<2时,-2<-x0<2,所以-3=3,矛盾.
③当x0≤-2时,-x0≥2,所以,所以.
因为函数是减函数,
所以m≥-1.
综上所述,实数m的取值范围是[-1,1).
21.解:(1)原问题等价于函数f(x)的值域为R.
当x≥0时,f(x)=x2-2x+2=(x-1)2+1≥1,
所以,函数y=f(x)在区间[0,+∞)上的值域为[1,+∞);
当x<0时,
,
则函数y=f(x)在区间(-∞,0)上单调递增,
此时f(x)<a.
所以,函数y=f(x)在区间(-∞,0)上的值域为(-∞,a).
由题意可得(-∞,a)∪[1,+∞)=R,
所以a≥1.
因此,实数a的取值范围是[1,+∞).
(2)当a=2时,
可知x=0不是方程f(x)=kx的根,
当x≠0时,由f(x)=kx,得,
令,
则
所以,直线y=k与函数y=g(x)的图象有三个公共点.
当x>0时,函数y=g(x)的单调递减区间为,单调递增区间为,
所以当时,函数y=g(x)取得最小值,
即;
当x<0时,,
则函数g(x)在区间(-∞,0)上为减函数.
作出函数y=g(x)和直线y=k的图象如图所示,
由图象可知,当时,直线y=k与函数y=g(x)的图象有三个交点,
因此,实数k的取值范围是.
22.(1)证明:因为x0是方程的根,
所以,即,
则,
所以是方程的根.
(2)解:由题意知,方程,的根分别是x1,x2,
即方程
,的根分别为x1,x2,
令t=x-1,
则方程,的根分别为t1=x1-1,t2=x2-1,
由(1)知t1是方程的根,
则是方程的根.
令,则是函数h(t)的零点,
又因为h(t)是区间(0,+∞)上的增函数,
所以是函数h(t)的唯一零点,
即是方程的唯一实根.
所以,
所以,
即,
所以
.
理科数学·函数与方程、函数的应用
2020.10.16
一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1.方程的根所在的区间为
A.(0,1)
B.(1,2)
C.(2,3)
D.(3,4)
2.某建材商场国庆期间搞促销活动,规定:顾客购物总金额不超过800元,不享受任何折扣;如果顾客购物总金额超过800元,则超过800元的部分享受一定的折扣优惠,并按下表折扣分别累计计算.
可以享受折扣优惠金额
折扣率
不超过500元的部分
5%
超过500元的部分
10%
若某顾客在此商场获得的折扣金额为50元,则此人购物实际所支付金额为
A.1500元
B.1550元
C.1750元
D.1800元
3.已知函数则使函数g(x)=f(x)+x-m有零点的实数m的取值范围是
A.[0,1)
B.(-∞,1)
C.(-∞,1]∪(2,+∞)
D.(-∞,0]∪(1,+∞)
4.某高校为提升科研能力,计划逐年加大科研经费投入.若该高校2018年全年投入科研经费1300万元,在此基础上,每年投入的科研经费比上一年增长12%,则该高校全年投入的科研经费开始超过2000万元的年份是(参考数据:lg
1.12≈0.05,lg
1.3≈0.11,lg
2≈0.30)
A.2020年
B.2021年
C.2022年
D.2023年
5.已知奇函数f(x)是R上的单调函数,若函数y=f(2x2+1)+f(λ-x)只有一个零点,则实数λ的值是
A.
B.
C.
D.
6.已知函数记g(x)=f(x)-ex-a,若函数g(x)存在三个零点,则实数a的取值范围是
A.
B.(-2e,-e)
C.
D.
7.设方程10x=|lg(-x)|的两个根分别为x1,x2,则
A.x1x2<0
B.x1x2=0
C.x1x2>1
D.0<x1x2<1
8.已知函数f(x)=lg|x-1|,,若两个函数图象的交点分别为P1(x1,y1),P2(x2,y2),P3(x3,y3),…,Pn(xn,yn),则x1+x2+x3+…+xn=
A.8
B.10
C.12
D.14
二、多项选择题(在每小题给出的选项中,有多项符合题目要求.)
9.若a<b<c,则函数f(x)=(x-a)(x-b)+(x-b)(x-c)+(x-c)(x-a)的两个零点所在的区间为
A.(-∞,a)
B.(a,b)
C.(b,c)
D.(c,+∞)
10.已知f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2-3x,则函数g(x)=f(x)-x+3的零点为
A.1
B.3
C.
D.
11.已知定义在R上的函数y=f(x)对任意的x都满足f(x+2)=f(x),当-1≤x<1时,
.若函数g(x)=f(x)-loga|x|至少有6个零点,则实数a的取值范围是
A.
B.(5,+∞)
C.
D.[5,7)
12.已知函数则以下结论正确的是
A.f(-3)+f(2019)=-3
B.f(x)在区间[4,5]上是增函数
C.若方程f(x)=kx+1恰有3个实根,则
D.若函数y=f(x)-b在区间(-∞,4)上有6个零点分别为xi(i=1,2,3,4,5,6),则的取值范围是(0,6)
三、填空题
13.声音的等级f(x)(单位:dB)与声音强度x(单位:W/m2)满足.喷气式飞机起飞时,声音的等级约为140
dB;一般说话时,声音的等级约为60
dB.那么喷气式飞机起飞时声音强度约为一般说话时声音强度的________倍.
14.函数的零点个数为________.
15.某企业准备投入适当的广告费对甲产品进行促销宣传,在一年内预计销售量y(单位:万件)与广告费x(单位:万元)之间的函数关系为.已知生产此产品的年固定投入为4万元,每生产1万件此产品仍需再投入30万元,且能全部售完.若每件甲产品售价(单位:元)定为“平均每件甲产品所占生产成本的150%”与“年平均每件甲产品所占广告费的50%”之和,则年利润W=___________(用x表示),当广告费为1万元时,该企业甲产品的年利润为________万元.
16.设函数若对任意实数b,关于x的方程f(x)-b=0总有实数根,则实数a的取值范围是________.
四、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17.已知函数f(x)=x2-(k-2)x+k2+3k+5有两个零点.
(1)若函数的两个零点是-1和-3,求实数k的值;
(2)若函数的两个零点是α和β,求α2+β2的取值范围.
18.噪声污染已经成为影响人们身体健康和生活质量的严重问题.实践证明,声音强度D(分贝)由公式D=alg
I+b(a,b为非零常数)给出,其中I(W/cm2)为声音能量.
(1)当声音强度D1,D2,D3满足D1+2D2=3D3时,求对应的声音能量I1,I2,I3满足的等量关系式.
(2)当人们低声说话,声音能量为10-13
W/cm2时,声音强度为30分贝;当人们正常说话,声音能量为10-12
W/cm2时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪?
19.“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度v(单位:千克/年)是养殖密度x(单位:尾/立方米)的函数.当x不超过4尾/立方米时,v的值为2(千克/年);当4≤x≤20时,v是x的一次函数;当x达到20尾/立方米时,因缺氧等原因,v的值为0(千克/年).
(1)当0<x≤20时,求函数v(x)的解析式.
(2)当养殖密度x为多大时,鱼的年生长量(单位:千克/立方米)f(x)=x·v(x)可以达到最大?并求出最大值.
20.对于函数f(x),若在定义域内存在实数x0,满足f(-x0)=-f(x0),则称f(x)为“M类函数”.
(1)设f(x)=2x+m是定义在区间[-1,1]上的“M类函数”,求实数m的最小值;
(2)若函数为其定义域上的“M类函数”,求实数m的取值范围.
21.已知函数.
(1)若对任意实数m,关于x的方程f(x)=m总有实数解,求a的取值范围;
(2)若a=2,求使得关于x的方程f(x)=kx有三个实数解的实数k的取值范围.
22.已知函数f(x)=2x,g(x)=log2x.
(1)若x0是方程的根,证明:是方程的根.
(2)设方程,的根分别是x1,x2,求x1+x2的值.
安康中学2020—2021学年度高三一轮复习周测卷(五)
理科数学·函数与方程、函数的应用
2020.10.16
参考答案
一、单项选择题(在每小题给出的四个选项中,只有一项是符合题目要求的)
1.【解析】令,由,,,所以f(1)·f(2)<0,又函数f(x)单调递增,所以f(x)的零点所在的区间为(1,2),故方程
的根所在区间为(1,2).故选B.
2.【解析】设此商场购物总金额为x元,可以获得的折扣金额为y元,由题设可知,
因为y=50>25,所以x>1300,所以0.1×(x-1300)+25=50,解得x=1550,故此人购物实际所支付金额为1550-50=1500(元).故选A.
3.【解析】函数g(x)=f(x)+x-m有零点等价于方程f(x)+x=m有实根,令
画出函数h(x)的大致图象(图略).观察它与直线y=m的交点,得知当m≤0或m>1时,有交点,即函数g(x)=f(x)+x-m有零点.故选D.
4.【解析】若2019年是第1年,则第n年全年投入的科研经费为1300×1.12n万元,由1300×1.12n>2000可得1.3×1.12n>2,所以lg
1.3+nlg
1.12>lg
2,所以n×0.05>0.19,得n>3.8,则正整数n的最小值为4,所以第4年,即2022年全年投入的科研经费开始超过2000万元.故选C.
5.【解析】因为函数y=f(2x2+1)+f(λ-x)只有一个零点,所以方程f(2x2+1)+f(λ-x)=0只有一个实数根.又奇函数f(x)是定义在R上的单调函数,则f(2x2+1)=-f(λ-x)等价于f(2x2+1)=f(x-λ),则2x2+1=x-λ,所以方程2x2-x+1+λ=0只有一个实数根,所以Δ=(-1)2-4×2×(1+λ)=0,解得.故选D.
6.【解析】由题意知函数y=f(x)与y=ex+a的图象有三个交点,作出函数y=f(x)的图象如图所示,当直线y=ex+a经过点时,;当直线y=ex+a经过点B(1,0)时,a=-e.因为函数y=f(x)与y=ex+a的图象有三个交点,所以.故选A.
7.【解析】作出函数y=10x与y=|lg(-x)|的大致图象,如图.显然x1<0,x2<0.不妨令x1<x2,则x1<-1<x2<0,所以,,此时,即lg(-x1)<-lg(-x2),由此得lg(x1x2)<0,所以0<x1x2<1.故选D.
8.【解析】作出函数f(x)=lg|x-1|与的图象如图所示,可知函数f(x)=lg|x-1|与函数的图象都关于直线x=1对称,当x<-9或x>11时,f(x)=lg|x-1|>1,此时,两函数图象没有交点,由图象知,两个函数图象共有10个交点,这些交点中有5对关于直线x=1对称,因此,x1+x2+x3+…+x10=2×5=10.故选B.
二、多项选择题(在每小题给出的选项中,有多项符合题目要求.)
9.【解析】因为a<b<c,所以f(a)=(a-b)(a-c)>0,f(b)=(b-c)(b-a)<0,f(c)=(c-a)(c-b)>0,由函数零点存在性定理可知,在区间(a,b),(b,c)内分别存在零点,又函数f(x)是二次函数,最多有两个零点.因此函数f(x)的两个零点分别位于区间(a,b),(b,c)内.故选BC.
10.【解析】令g(x)=0,即f(x)-x+3=0,所以f(x)=x-3,作出函数y=f(x)与y=x-3的图象,如图所示,有3个交点.
y轴右侧有2个交点,其零点为1和3;y轴左侧零点x<-3.D项符合题意.故选ABD.
11.【解析】当a>1时,作出函数f(x)与函数y=loga|x|的图象,如图所示.
结合图象可知,解得a>5;当0<a<1时,作出函数f(x)与函数y=loga|x|的图象,如图所示.
结合图象可知,解得.故选AB.
12.【解析】函数f(x)的图象如图所示,f(-3)=-9+6=-3,f(2019)=f(1)=f(-1)=1,所以f(-3)+f(2019)=-2,故A错误;由图象可知f(x)在区间[4,5]上是增函数,故B正确;由图象可知当时,直线f(x)=kx+1与函数图象恰有3个交点,故C正确;由图象可得,当函数y=f(x)-b在区间(-∞,4)上有6个零点分别为xi(i=1,2,3,4,5,6)时,则0<b<1,所以当b趋近于0时,趋近于0;当b趋近于1时,趋近于6,所以的取值范围是(0,6),故D正确.故选BCD.
三、填空题
13.108
【解析】设喷气式飞机起飞时声音强度和一般说话时声音强度分别为x1,x2,由题意可得,解得x1=102;,解得x2=10-6,所以.因此喷气式飞机起飞时声音强度约为一般说话时声音强度的108倍.
14.2
【解析】令f(x)=0,得,显然x=-2不是该方程的根,故
,在同一直角坐标系中分别作出函数,的图象如图所示,可知,它们有2个交点,即函数有2个零点.
15.
31.5
【解析】由题意可得产品的生产成本为(30y+4)万元,销售单价为,故年销售收入为
.所以年利润(万元).所以当广告费为1万元,即x=1时,该企业甲产品的年利润为(万元).
16.[0,1]
【解析】若对任意实数b,关于x的方程f(x)-b=0总有实数根,即对任意实数b,函数f(x)的图象与直线y=b总有交点,即函数f(x)的值域为R,因为在同一坐标系中画出函数y=x与y=x2的图象,如图所示,由图可得:当a∈[0,1]时,函数f(x)的值域为R,故实数a的取值范围是[0,1].
四、解答题(解答应写出必要的文字说明、证明过程或演算步骤)
17.解:(1)由于-1和-3是函数f(x)的两个零点,
故-1和-3是方程x2-(k-2)x+k2+3k+5=0的两个实数根,
则解得k=-2.
(2)若函数的两个零点为α和β,则α和β是方程x2-(k-2)x+k2+3k+5=0的两根,
所以
则,且α2+β2=(α+β)2-2αβ=-k2-10k-6在区间上单调递减,
所以α2+β2在区间上的最大值是18,最小值是,所以α2+β2的取值范围是.
18.解:(1)因为D1+2D2=3D3,
所以alg
I1+b+2(alg
I2+b)=3(alg
I3+b),
所以lg
I1+2lg
I2=3lg
I3,所以.
(2)由题意得解得
所以100<10lg
I+160<120,解得10-6<I<10-4.
所以,当声音能量I∈(10-6,10-4)时,人会暂时性失聪.
19.解:(1)由题意可知,当0<x≤4时,v(x)=2;
当4≤x≤20时,设v(x)=ax+b(a≠0),
显然v(x)=ax+b在区间[4,20]上是减函数,
则解得
故函数
(2)依题意并由(1)可得,
当0<x≤4时,f(x)为增函数,
故f(x)max=f(4)=8;
当4<x≤20时,,
故f(x)max=f(10)=12.5.
所以当养殖密度为10尾/立方米时,鱼的年生长量可以达到最大,最大值约为12.5千克/立方米.
20.解:(1)因为函数f(x)=2x+m是定义在区间[-1,1]上的“M类函数”,
所以存在实数x0∈[-1,1],满足f(-x0)=-f(x0),
即方程2x+2-x+2m=0在区间[-1,1]上有解.
令t=2x,,则.
令,因为函数g(t)在区间上单调递增,在区间[1,2]上单调递减,
所以当或t=2时,m取得最小值.
(2)由x2-2mx>0对?x≥2恒成立,得m<1.
因为若函数为其定义域上的“M类函数”,
所以存在实数x0,满足f(-x0)=-f(x0),
①当x0≥2时,-x0≤-2,
所以,所以.
因为函数是增函数,所以m≥-1.
②当-2<x0<2时,-2<-x0<2,所以-3=3,矛盾.
③当x0≤-2时,-x0≥2,所以,所以.
因为函数是减函数,
所以m≥-1.
综上所述,实数m的取值范围是[-1,1).
21.解:(1)原问题等价于函数f(x)的值域为R.
当x≥0时,f(x)=x2-2x+2=(x-1)2+1≥1,
所以,函数y=f(x)在区间[0,+∞)上的值域为[1,+∞);
当x<0时,
,
则函数y=f(x)在区间(-∞,0)上单调递增,
此时f(x)<a.
所以,函数y=f(x)在区间(-∞,0)上的值域为(-∞,a).
由题意可得(-∞,a)∪[1,+∞)=R,
所以a≥1.
因此,实数a的取值范围是[1,+∞).
(2)当a=2时,
可知x=0不是方程f(x)=kx的根,
当x≠0时,由f(x)=kx,得,
令,
则
所以,直线y=k与函数y=g(x)的图象有三个公共点.
当x>0时,函数y=g(x)的单调递减区间为,单调递增区间为,
所以当时,函数y=g(x)取得最小值,
即;
当x<0时,,
则函数g(x)在区间(-∞,0)上为减函数.
作出函数y=g(x)和直线y=k的图象如图所示,
由图象可知,当时,直线y=k与函数y=g(x)的图象有三个交点,
因此,实数k的取值范围是.
22.(1)证明:因为x0是方程的根,
所以,即,
则,
所以是方程的根.
(2)解:由题意知,方程,的根分别是x1,x2,
即方程
,的根分别为x1,x2,
令t=x-1,
则方程,的根分别为t1=x1-1,t2=x2-1,
由(1)知t1是方程的根,
则是方程的根.
令,则是函数h(t)的零点,
又因为h(t)是区间(0,+∞)上的增函数,
所以是函数h(t)的唯一零点,
即是方程的唯一实根.
所以,
所以,
即,
所以
.
同课章节目录
