初中数学暑期讲义——直线和圆的位置关系(无答案)
文档属性
| 名称 | 初中数学暑期讲义——直线和圆的位置关系(无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 186.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-10-07 23:20:44 | ||
图片预览

文档简介
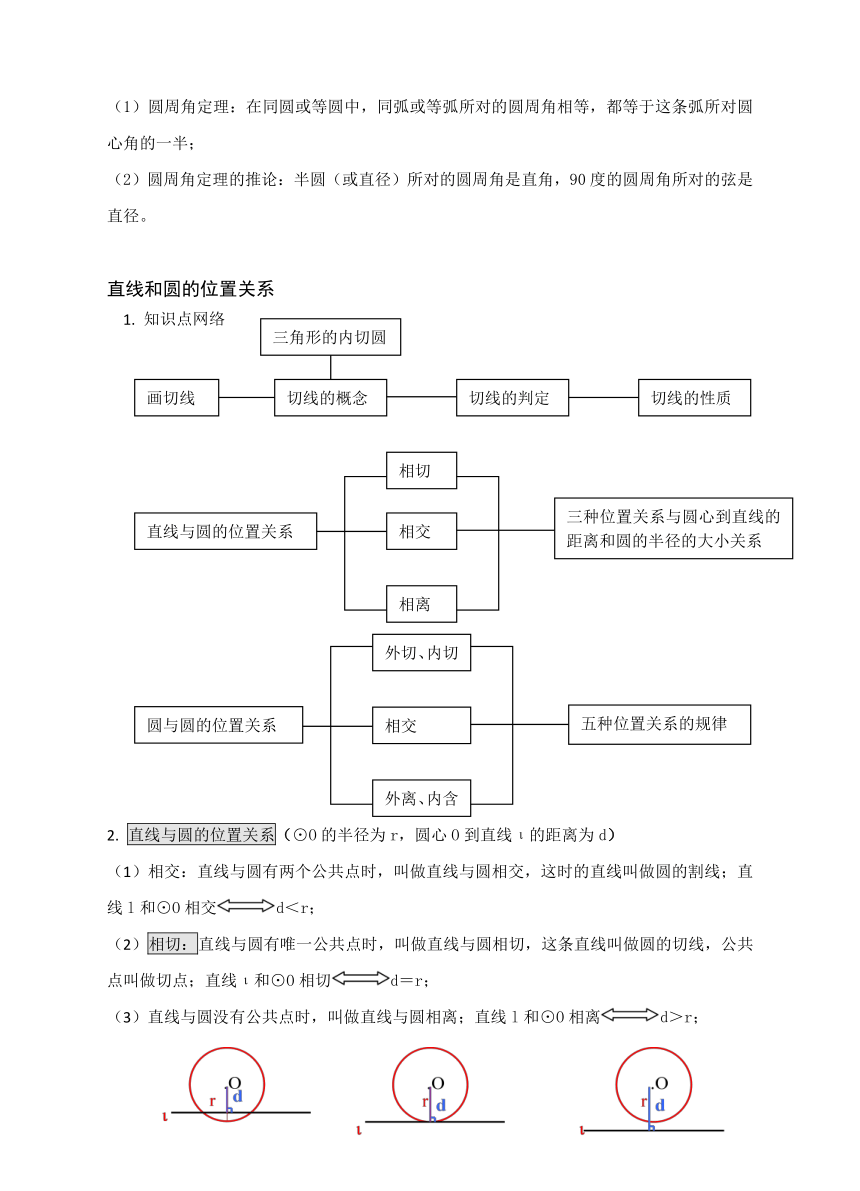
第七讲 圆(二)
——直线和圆的位置关系
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性
2. 垂径定理及其推论:
(1)定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;
(2)推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧。
垂径定理归纳为:一条直线,如果具有:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧。这五条中可以“知二推三”。
但应注意:②③为条件时,即“经过圆心平分弦”,必须是非直径的弦,因为圆的任何两条直径都互相平分。
3 . 垂径定理的推论:圆的两条平行弦所夹的弧相等.
4. 弧﹑弦﹑圆心角之间的关系
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
(2)在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距,如果有一组量相等,那么它们所对应的其余各组量都分别相等.
5. 圆周角定理及其推论
(1)圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对圆心角的一半;
(2)圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。
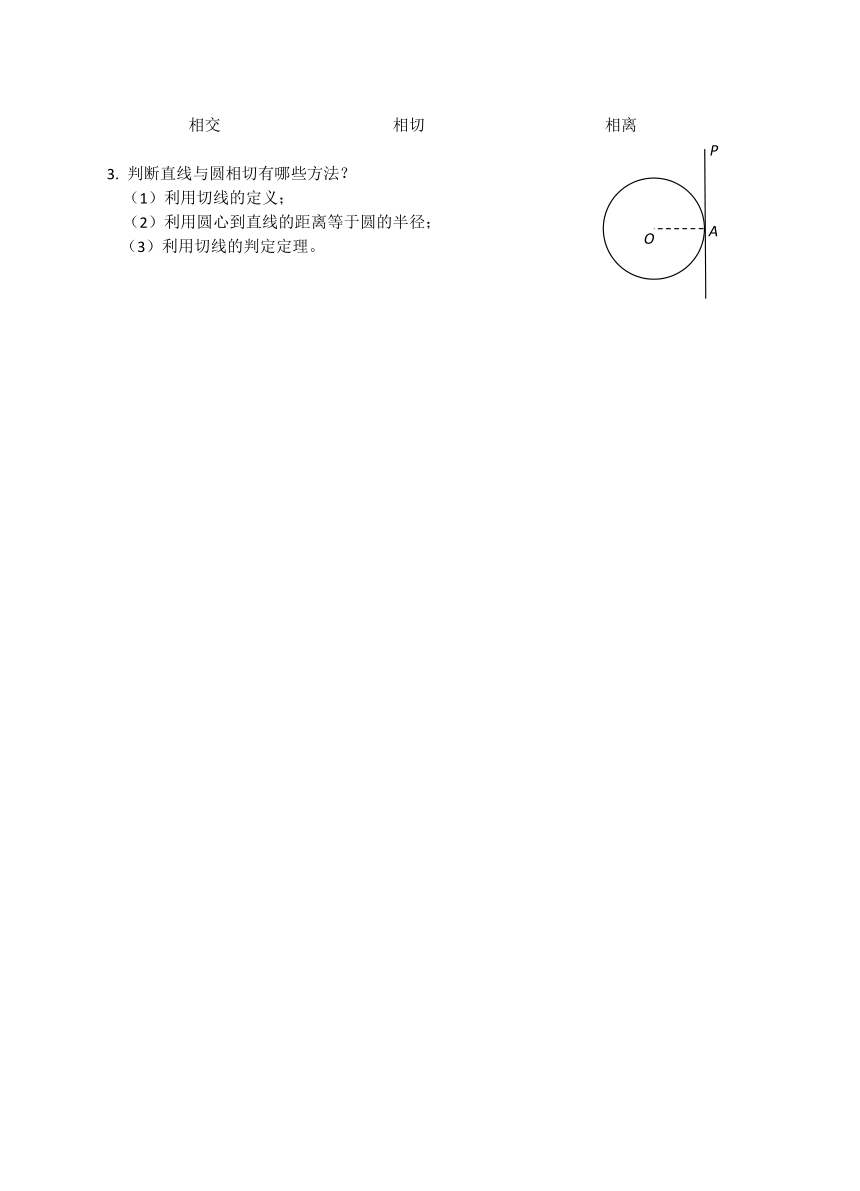
直线和圆的位置关系
1. 知识点网络
2. 直线与圆的位置关系(⊙O的半径为r,圆心O到直线ι的距离为d)
(1)相交:直线与圆有两个公共点时,叫做直线与圆相交,这时的直线叫做圆的割线;直线l和⊙O相交d<r;
(2)相切:直线与圆有唯一公共点时,叫做直线与圆相切,这条直线叫做圆的切线,公共点叫做切点;直线ι和⊙O相切d=r;
(3)直线与圆没有公共点时,叫做直线与圆相离;直线l和⊙O相离d>r;
相交 相切 相离
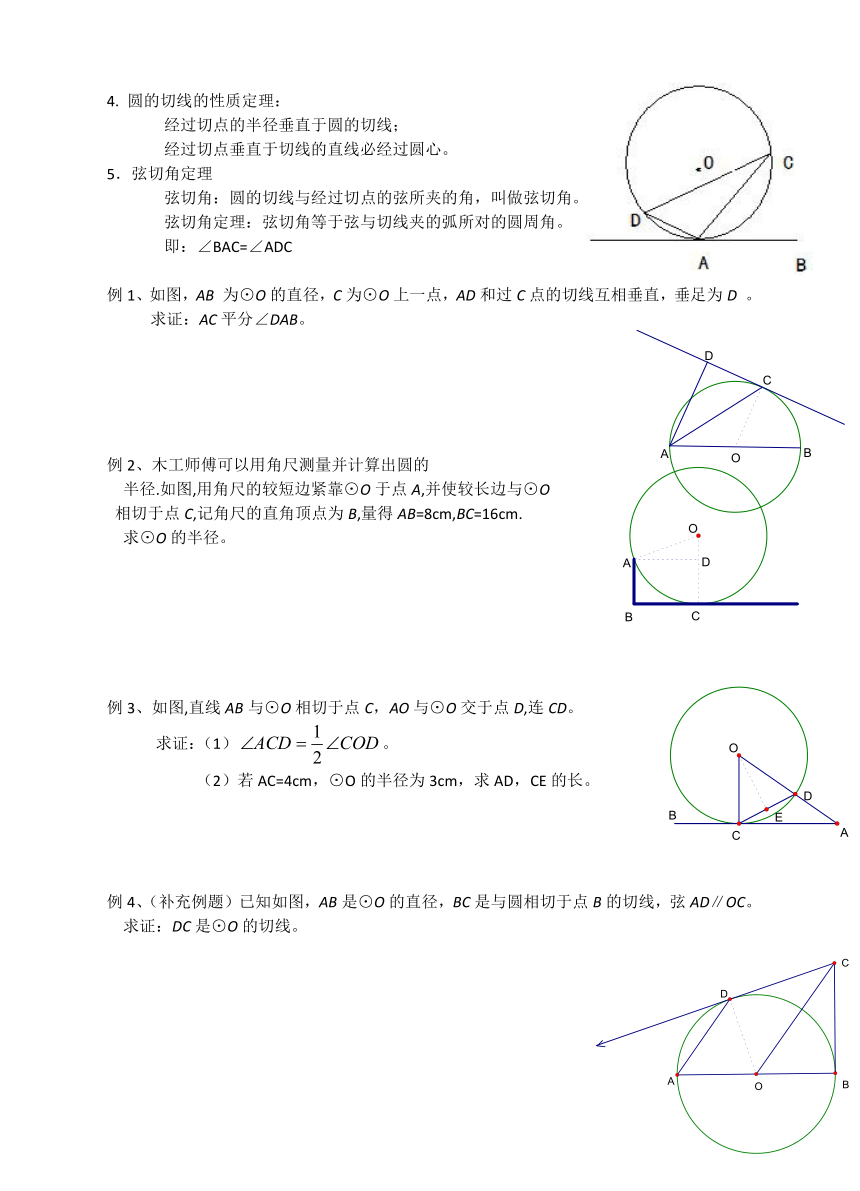
3. 判断直线与圆相切有哪些方法?
(1)利用切线的定义;
(2)利用圆心到直线的距离等于圆的半径;
(3)利用切线的判定定理。
4. 圆的切线的性质定理:
经过切点的半径垂直于圆的切线;
经过切点垂直于切线的直线必经过圆心。
5.弦切角定理
弦切角:圆的切线与经过切点的弦所夹的角,叫做弦切角。
弦切角定理:弦切角等于弦与切线夹的弧所对的圆周角。
即:∠BAC=∠ADC
例1、如图,AB 为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D 。
求证:AC平分∠DAB。
例2、木工师傅可以用角尺测量并计算出圆的
半径.如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O
相切于点C,记角尺的直角顶点为B,量得AB=8cm,BC=16cm.
求⊙O的半径。
例3、如图,直线AB与⊙O相切于点C,AO与⊙O交于点D,连CD。
求证:(1)。
(2)若AC=4cm,⊙O的半径为3cm,求AD,CE的长。
例4、(补充例题)已知如图,AB是⊙O的直径,BC是与圆相切于点B的切线,弦AD∥OC。
求证:DC是⊙O的切线。
补充:圆幂定理
圆幂的定义:一点P对半径R的圆O的幂定义如下:
所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
圆幂定理是相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们推论的统称。
相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
如图,AB、CD为圆O的两条任意弦。相交于点P,连接AD、BC,则∠D=∠B,
∠A=∠C。所以△APD∽△BPC。所以
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆焦点的两条线段长的比例中项。
如图,PT为圆切线,PAB为割线。连接TA,TB,则∠PTA=∠B(弦切角等于同弧圆周角)
所以△PTA∽△PBT,所以
割线定理:从圆外一点P引两条割线与圆分别交于A.B.C.D 则有 PA·PB=PC·PD。
这个证明就比较简单了。可以过P做圆的切线,也可以连接CB和AD。证相似。
存在:
进一步升华(推论):
过任意在圆O外的一点P引一条直线L1与一条过圆心的直线L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D。则PA·PB=PC·PD。若圆半径为r,则
(一定要加绝对值,原因见下)为定值。这个值称为点P到圆O的幂。(事实上所有的过P点与圆相交的直线都满足这个值)
若点P在圆内,类似可得定值为
故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差的绝
对值。(这就是“圆幂”的由来)
练习
1. (2011四川成都,10,3分)已知⊙O的面积为,若点0到直线的距离为,则直线与⊙O的位置关系是 (A)相交 (B)相切 (C)相离 (D)无法确定
2. (2011重庆綦江,7,4分) 如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,
OA=3,那么∠AOB所对弧的长度为( )
A.6л B.5л C.3л D.2л
3. (2011湖北黄冈,13,3分)如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=( )
A.30° B.45° C.60° D.67.5°
4. (2011山东东营,12,3分)如图,直线与x轴、y分别相交与A、B
两点,圆心P的坐标为(1,0),圆P与y轴相切与点O。若将圆P沿x轴向左移动,
当圆P与该直线相交时,横坐标为整数的点P′的个数是( )
A.2 B.3 C.4 D. 5
5. (2011浙江杭州,5,3)在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
6. (2011山东枣庄,7,3分)如图,是的切线,切点为A,PA=2,
∠APO=30°,则的半径为( )
A.1 B. C.2 D.4
7. (2011四川南充市,13,3分)如图,PA,PB是⊙O是切线,A,B为切点,
AC是⊙O的直径,若∠BAC=25°,则∠P= __________度.
8. (2011江苏苏州,16,3分)如图,已知AB是⊙O的一条直径,延长AB至C点,
使得AC=3BC,CD与⊙O相切,切点为D.若CD=,则线段BC的长度等于________
9. (2010湖北孝感,18,3分)如图,直径分别为CD、CE的两个半圆相切于点C,
大半圆M的弦AB与小半圆N相切于点F,且AB∥CD,AB=4,设、的长
分别为x、y,线段ED的长为z,则z(x+y)= .
10. (2011安徽芜湖,23,12分)如图,已知直线交⊙O于A、B两点,AE是⊙O的直径,
点C为⊙O上一点,且AC平分∠PAE,过C作,垂足为D.
(1) 求证:CD为⊙O的切线;
(2) 若DC+DA=6,⊙O的直径为10,求AB的长度.
11. (2011山东菏泽,18,10分)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,
AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
12. (2011浙江省嘉兴,22,12分)如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=,tan∠AEC=,求圆的直径.
13. (2011湖南永州,23,10分)如图,AB是半圆O的直径,点C是⊙O上一点
(不与A,B重合),连接AC,BC,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,连接EB,使∠OEB=∠ABC.
⑴求证:BE是⊙O的切线;
⑵若OA=10,BC=16,求BE的长.
14. (2011四川广安,29,10分)如图8所示.P是⊙O外一点.
PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,
并延长BO与切线PA相交于点Q.
(1)求证:PB是⊙O的切线;
(2)求证: AQ PQ= OQ BQ;
(3)设∠AOQ=.若cos=.OQ= 15.求AB的长
三角形的内切圆
切线的概念
画切线
切线的判定
切线的性质
直线与圆的位置关系
相切
相交
相离
三种位置关系与圆心到直线的距离和圆的半径的大小关系
圆与圆的位置关系
外切、内切
相交
外离、内含
五种位置关系的规律
P
O
A
C
D
A
O
P
B
第13题图
O
P
A
_
Q
_
P
_
O
_
B
_
A
图8
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
——直线和圆的位置关系
一个圆绕着它的圆心旋转任意一个角度,都能与原来的图形重合.这是圆特有的一个性质:圆的旋转不变性
2. 垂径定理及其推论:
(1)定理:垂直于弦的直径平分这条弦,并且平分这条弦所对的两条弧;
(2)推论:平分弦(不是直径)的直径垂直于这条弦,并且平分这条弦所对的两条弧。
垂径定理归纳为:一条直线,如果具有:①经过圆心;②垂直于弦;③平分弦;④平分弦所对的优弧;⑤平分弦所对的劣弧。这五条中可以“知二推三”。
但应注意:②③为条件时,即“经过圆心平分弦”,必须是非直径的弦,因为圆的任何两条直径都互相平分。
3 . 垂径定理的推论:圆的两条平行弦所夹的弧相等.
4. 弧﹑弦﹑圆心角之间的关系
(1)在同圆或等圆中,相等的圆心角所对的弧相等,所对的弦也相等。
(2)在同圆或等圆中,如果①两个圆心角,②两条弧,③两条弦,④两条弦心距,如果有一组量相等,那么它们所对应的其余各组量都分别相等.
5. 圆周角定理及其推论
(1)圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对圆心角的一半;
(2)圆周角定理的推论:半圆(或直径)所对的圆周角是直角,90度的圆周角所对的弦是直径。
直线和圆的位置关系
1. 知识点网络
2. 直线与圆的位置关系(⊙O的半径为r,圆心O到直线ι的距离为d)
(1)相交:直线与圆有两个公共点时,叫做直线与圆相交,这时的直线叫做圆的割线;直线l和⊙O相交d<r;
(2)相切:直线与圆有唯一公共点时,叫做直线与圆相切,这条直线叫做圆的切线,公共点叫做切点;直线ι和⊙O相切d=r;
(3)直线与圆没有公共点时,叫做直线与圆相离;直线l和⊙O相离d>r;
相交 相切 相离
3. 判断直线与圆相切有哪些方法?
(1)利用切线的定义;
(2)利用圆心到直线的距离等于圆的半径;
(3)利用切线的判定定理。
4. 圆的切线的性质定理:
经过切点的半径垂直于圆的切线;
经过切点垂直于切线的直线必经过圆心。
5.弦切角定理
弦切角:圆的切线与经过切点的弦所夹的角,叫做弦切角。
弦切角定理:弦切角等于弦与切线夹的弧所对的圆周角。
即:∠BAC=∠ADC
例1、如图,AB 为⊙O的直径,C为⊙O上一点,AD和过C点的切线互相垂直,垂足为D 。
求证:AC平分∠DAB。
例2、木工师傅可以用角尺测量并计算出圆的
半径.如图,用角尺的较短边紧靠⊙O于点A,并使较长边与⊙O
相切于点C,记角尺的直角顶点为B,量得AB=8cm,BC=16cm.
求⊙O的半径。
例3、如图,直线AB与⊙O相切于点C,AO与⊙O交于点D,连CD。
求证:(1)。
(2)若AC=4cm,⊙O的半径为3cm,求AD,CE的长。
例4、(补充例题)已知如图,AB是⊙O的直径,BC是与圆相切于点B的切线,弦AD∥OC。
求证:DC是⊙O的切线。
补充:圆幂定理
圆幂的定义:一点P对半径R的圆O的幂定义如下:
所以圆内的点的幂为负数,圆外的点的幂为正数,圆上的点的幂为零。
圆幂定理是相交弦定理、切割线定理及割线定理(切割线定理推论)以及他们推论的统称。
相交弦定理:圆内的两条相交弦,被交点分成的两条线段长的积相等。
如图,AB、CD为圆O的两条任意弦。相交于点P,连接AD、BC,则∠D=∠B,
∠A=∠C。所以△APD∽△BPC。所以
切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆焦点的两条线段长的比例中项。
如图,PT为圆切线,PAB为割线。连接TA,TB,则∠PTA=∠B(弦切角等于同弧圆周角)
所以△PTA∽△PBT,所以
割线定理:从圆外一点P引两条割线与圆分别交于A.B.C.D 则有 PA·PB=PC·PD。
这个证明就比较简单了。可以过P做圆的切线,也可以连接CB和AD。证相似。
存在:
进一步升华(推论):
过任意在圆O外的一点P引一条直线L1与一条过圆心的直线L2,L1与圆交于A、B(可重合,即切线),L2与圆交于C、D。则PA·PB=PC·PD。若圆半径为r,则
(一定要加绝对值,原因见下)为定值。这个值称为点P到圆O的幂。(事实上所有的过P点与圆相交的直线都满足这个值)
若点P在圆内,类似可得定值为
故平面上任意一点对于圆的幂为这个点到圆心的距离与圆的半径的平方差的绝
对值。(这就是“圆幂”的由来)
练习
1. (2011四川成都,10,3分)已知⊙O的面积为,若点0到直线的距离为,则直线与⊙O的位置关系是 (A)相交 (B)相切 (C)相离 (D)无法确定
2. (2011重庆綦江,7,4分) 如图,PA、PB是⊙O的切线,切点是A、B,已知∠P=60°,
OA=3,那么∠AOB所对弧的长度为( )
A.6л B.5л C.3л D.2л
3. (2011湖北黄冈,13,3分)如图,AB为⊙O的直径,PD切⊙O于点C,交AB的延长线于D,且CO=CD,则∠PCA=( )
A.30° B.45° C.60° D.67.5°
4. (2011山东东营,12,3分)如图,直线与x轴、y分别相交与A、B
两点,圆心P的坐标为(1,0),圆P与y轴相切与点O。若将圆P沿x轴向左移动,
当圆P与该直线相交时,横坐标为整数的点P′的个数是( )
A.2 B.3 C.4 D. 5
5. (2011浙江杭州,5,3)在平面直角坐标系xOy中,以点(-3,4)为圆心,4为半径的圆( )
A.与x轴相交,与y轴相切 B.与x轴相离,与y轴相交
C.与x轴相切,与y轴相交 D.与x轴相切,与y轴相离
6. (2011山东枣庄,7,3分)如图,是的切线,切点为A,PA=2,
∠APO=30°,则的半径为( )
A.1 B. C.2 D.4
7. (2011四川南充市,13,3分)如图,PA,PB是⊙O是切线,A,B为切点,
AC是⊙O的直径,若∠BAC=25°,则∠P= __________度.
8. (2011江苏苏州,16,3分)如图,已知AB是⊙O的一条直径,延长AB至C点,
使得AC=3BC,CD与⊙O相切,切点为D.若CD=,则线段BC的长度等于________
9. (2010湖北孝感,18,3分)如图,直径分别为CD、CE的两个半圆相切于点C,
大半圆M的弦AB与小半圆N相切于点F,且AB∥CD,AB=4,设、的长
分别为x、y,线段ED的长为z,则z(x+y)= .
10. (2011安徽芜湖,23,12分)如图,已知直线交⊙O于A、B两点,AE是⊙O的直径,
点C为⊙O上一点,且AC平分∠PAE,过C作,垂足为D.
(1) 求证:CD为⊙O的切线;
(2) 若DC+DA=6,⊙O的直径为10,求AB的长度.
11. (2011山东菏泽,18,10分)如图,BD为⊙O的直径,AB=AC,AD交BC于点E,
AE=2,ED=4,
(1)求证:△ABE∽△ADB;
(2)求AB的长;
(3)延长DB到F,使得BF=BO,连接FA,试判断直线FA与⊙O的位置关系,并说明理由.
12. (2011浙江省嘉兴,22,12分)如图,△ABC中,以BC为直径的圆交AB于点D,∠ACD=∠ABC.
(1)求证:CA是圆的切线;
(2)若点E是BC上一点,已知BE=6,tan∠ABC=,tan∠AEC=,求圆的直径.
13. (2011湖南永州,23,10分)如图,AB是半圆O的直径,点C是⊙O上一点
(不与A,B重合),连接AC,BC,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,连接EB,使∠OEB=∠ABC.
⑴求证:BE是⊙O的切线;
⑵若OA=10,BC=16,求BE的长.
14. (2011四川广安,29,10分)如图8所示.P是⊙O外一点.
PA是⊙O的切线.A是切点.B是⊙O上一点.且PA=PB,连接AO、BO、AB,
并延长BO与切线PA相交于点Q.
(1)求证:PB是⊙O的切线;
(2)求证: AQ PQ= OQ BQ;
(3)设∠AOQ=.若cos=.OQ= 15.求AB的长
三角形的内切圆
切线的概念
画切线
切线的判定
切线的性质
直线与圆的位置关系
相切
相交
相离
三种位置关系与圆心到直线的距离和圆的半径的大小关系
圆与圆的位置关系
外切、内切
相交
外离、内含
五种位置关系的规律
P
O
A
C
D
A
O
P
B
第13题图
O
P
A
_
Q
_
P
_
O
_
B
_
A
图8
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 1 页)
同课章节目录
