六年级下册数学试题-小升初专题培优:五大模型(含答案)全国通用
文档属性
| 名称 | 六年级下册数学试题-小升初专题培优:五大模型(含答案)全国通用 |
|
|
| 格式 | docx | ||
| 文件大小 | 605.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-25 21:49:57 | ||
图片预览



文档简介
小升初——五大模型
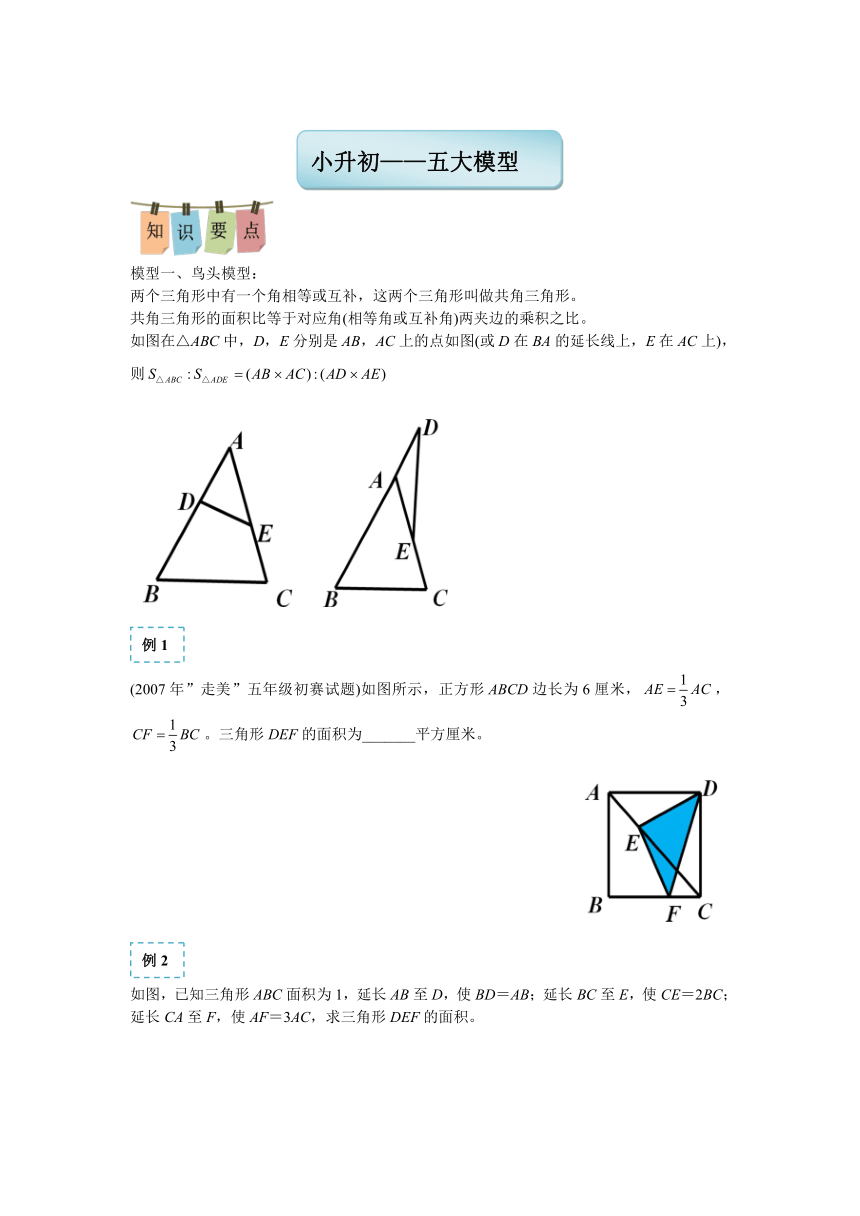
模型一、鸟头模型:
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在△ABC中,D,E分别是AB,AC上的点如图(或D在BA的延长线上,E在AC上),
则false
例1
(2007年”走美”五年级初赛试题)如图所示,正方形ABCD边长为6厘米,false,false。三角形DEF的面积为_______平方厘米。
例2
如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。
例3
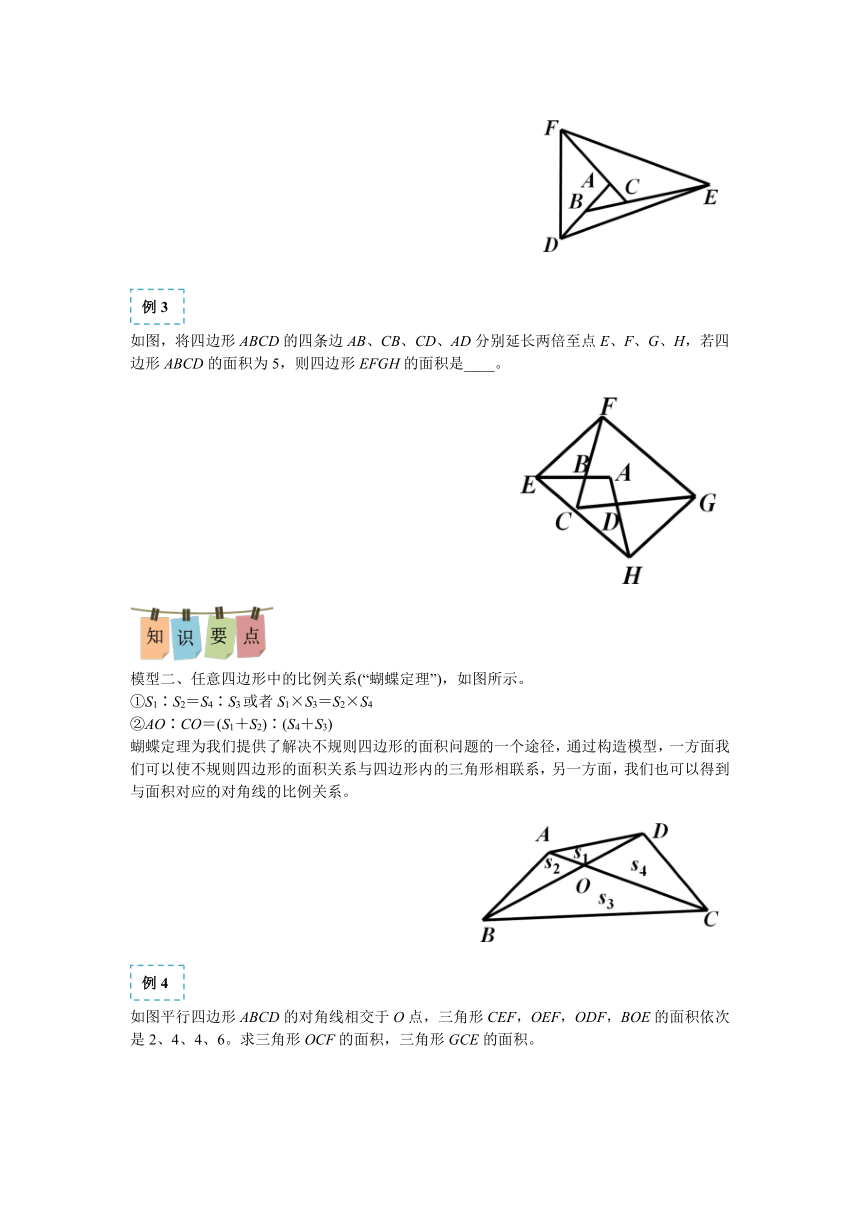
如图,将四边形ABCD的四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H,若四边形ABCD的面积为5,则四边形EFGH的面积是____。
模型二、任意四边形中的比例关系(“蝴蝶定理”),如图所示。
①S1∶S2=S4∶S3或者S1×S3=S2×S4
②AO∶CO=(S1+S2)∶(S4+S3)
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径,通过构造模型,一方面我们可以使不规则四边形的面积关系与四边形内的三角形相联系,另一方面,我们也可以得到与面积对应的对角线的比例关系。
例4
如图平行四边形ABCD的对角线相交于O点,三角形CEF,OEF,ODF,BOE的面积依次是2、4、4、6。求三角形OCF的面积,三角形GCE的面积。
例5
如图边长为1的正方形ABCD中,BE=2CE,F为DC的中点,求三角形AGE的面积。
模型三、梯形中的蝴蝶定理
①S1:S3=a2:b2
②S1:S3:S2:S4=a2:b2:ab:ab
③S的对应份数为(a+b)2
梯形蝴蝶定理,给我们提供了解决梯形面积与上下底之间关系互相转换的渠道。构造模型,直接应用结论,往往有事半功倍的效果。
例6
长方形ABCD分别被CE、DF分成四块,其中三块的面积分别是2、5、8平方厘米,那么余下的OFBC的面积是多少?
例7
如图所示,在边长为1的正方形ABCD中,BE=2EC,DF=2FC,求四边形ABGD的面积。
模型四:燕尾定理
在三角形ABC中,AD,BE,CF相交于同一点O,那么 。
上述定理给出了一个新的转化面积比与线段比的手段,因为△ABO和△ACO的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径。
例8
如右图,三角形ABC中,BD∶DC=4∶9,CE∶EA=4∶3,求AF∶FB。
例9
(2008年“学而思杯”六年级数学试题)如右图,三角形ABC中,AF∶FB=BD∶DC=CE∶AE=3∶2,且三角形ABC的面积是1,则三角形ABE的面积为______,三角形AGE的面积为________,三角形GHI的面积为______。
模型五:相似模型
①false
②S1∶S2=a2∶A2。
例10
如图在三角形ABC中,DE、FG、BC分别平行,且AD=DG=GB,求三角形ADE,四边形DEFG,四边形FGBC的面积之比。
例11
如图,正方形ABCD的边长为1,E、F分别为AB、BD的中点,GC=falseFC,求阴影部分的面积。
测试题
1.四边形ABCD的对角线AC与BD交于点O,如图所示。如果三角形ABD的面积等于三角形BCD的面积的,且AO=2,DO=3,那么CO的长度是DO的长度的几倍?
2.如下图,梯形ABCD的AB平行于CD,对角线交于点O,已知三角形ABO与三角形BCO的面积分别是25平方厘米和35平方厘米。那么梯形ABCD的面积是多少?
3.如右图,三角形false中,false,false,求false。
答案
1.答案:
三角形ABD的面积:三角形BCD的面积=AO:CO=1:3,那么CO=3AO=6,所以CO是DO的2倍。
2.答案:
三角形AOD的面积是35平方厘米,那么三角形COD的面积是35×35÷25=49平方厘米,那么梯形ABCD的面积为25+35+35+49=144平方厘米。
3.答案:
由题可知:三角形ABO的面积:三角形ACO的面积=3:4,三角形ABO的面积:三角形BCO的面积=5:6,那么三角形ABO的面积:三角形ACO的面积:三角形BCO的面积=15:20:18,那么AF:FB=20:18=10:9。
模型一、鸟头模型:
两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等于对应角(相等角或互补角)两夹边的乘积之比。
如图在△ABC中,D,E分别是AB,AC上的点如图(或D在BA的延长线上,E在AC上),
则false
例1
(2007年”走美”五年级初赛试题)如图所示,正方形ABCD边长为6厘米,false,false。三角形DEF的面积为_______平方厘米。
例2
如图,已知三角形ABC面积为1,延长AB至D,使BD=AB;延长BC至E,使CE=2BC;延长CA至F,使AF=3AC,求三角形DEF的面积。
例3
如图,将四边形ABCD的四条边AB、CB、CD、AD分别延长两倍至点E、F、G、H,若四边形ABCD的面积为5,则四边形EFGH的面积是____。
模型二、任意四边形中的比例关系(“蝴蝶定理”),如图所示。
①S1∶S2=S4∶S3或者S1×S3=S2×S4
②AO∶CO=(S1+S2)∶(S4+S3)
蝴蝶定理为我们提供了解决不规则四边形的面积问题的一个途径,通过构造模型,一方面我们可以使不规则四边形的面积关系与四边形内的三角形相联系,另一方面,我们也可以得到与面积对应的对角线的比例关系。
例4
如图平行四边形ABCD的对角线相交于O点,三角形CEF,OEF,ODF,BOE的面积依次是2、4、4、6。求三角形OCF的面积,三角形GCE的面积。
例5
如图边长为1的正方形ABCD中,BE=2CE,F为DC的中点,求三角形AGE的面积。
模型三、梯形中的蝴蝶定理
①S1:S3=a2:b2
②S1:S3:S2:S4=a2:b2:ab:ab
③S的对应份数为(a+b)2
梯形蝴蝶定理,给我们提供了解决梯形面积与上下底之间关系互相转换的渠道。构造模型,直接应用结论,往往有事半功倍的效果。
例6
长方形ABCD分别被CE、DF分成四块,其中三块的面积分别是2、5、8平方厘米,那么余下的OFBC的面积是多少?
例7
如图所示,在边长为1的正方形ABCD中,BE=2EC,DF=2FC,求四边形ABGD的面积。
模型四:燕尾定理
在三角形ABC中,AD,BE,CF相交于同一点O,那么 。
上述定理给出了一个新的转化面积比与线段比的手段,因为△ABO和△ACO的形状很象燕子的尾巴,所以这个定理被称为燕尾定理.该定理在许多几何题目中都有着广泛的运用,它的特殊性在于,它可以存在于任何一个三角形之中,为三角形中的三角形面积对应底边之间提供互相联系的途径。
例8
如右图,三角形ABC中,BD∶DC=4∶9,CE∶EA=4∶3,求AF∶FB。
例9
(2008年“学而思杯”六年级数学试题)如右图,三角形ABC中,AF∶FB=BD∶DC=CE∶AE=3∶2,且三角形ABC的面积是1,则三角形ABE的面积为______,三角形AGE的面积为________,三角形GHI的面积为______。
模型五:相似模型
①false
②S1∶S2=a2∶A2。
例10
如图在三角形ABC中,DE、FG、BC分别平行,且AD=DG=GB,求三角形ADE,四边形DEFG,四边形FGBC的面积之比。
例11
如图,正方形ABCD的边长为1,E、F分别为AB、BD的中点,GC=falseFC,求阴影部分的面积。
测试题
1.四边形ABCD的对角线AC与BD交于点O,如图所示。如果三角形ABD的面积等于三角形BCD的面积的,且AO=2,DO=3,那么CO的长度是DO的长度的几倍?
2.如下图,梯形ABCD的AB平行于CD,对角线交于点O,已知三角形ABO与三角形BCO的面积分别是25平方厘米和35平方厘米。那么梯形ABCD的面积是多少?
3.如右图,三角形false中,false,false,求false。
答案
1.答案:
三角形ABD的面积:三角形BCD的面积=AO:CO=1:3,那么CO=3AO=6,所以CO是DO的2倍。
2.答案:
三角形AOD的面积是35平方厘米,那么三角形COD的面积是35×35÷25=49平方厘米,那么梯形ABCD的面积为25+35+35+49=144平方厘米。
3.答案:
由题可知:三角形ABO的面积:三角形ACO的面积=3:4,三角形ABO的面积:三角形BCO的面积=5:6,那么三角形ABO的面积:三角形ACO的面积:三角形BCO的面积=15:20:18,那么AF:FB=20:18=10:9。
同课章节目录
