六年级下册数学试题-小升初专题培优:一半模型(含答案)全国通用
文档属性
| 名称 | 六年级下册数学试题-小升初专题培优:一半模型(含答案)全国通用 |
|
|
| 格式 | docx | ||
| 文件大小 | 255.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-10-25 21:51:52 | ||
图片预览

文档简介
一半模型
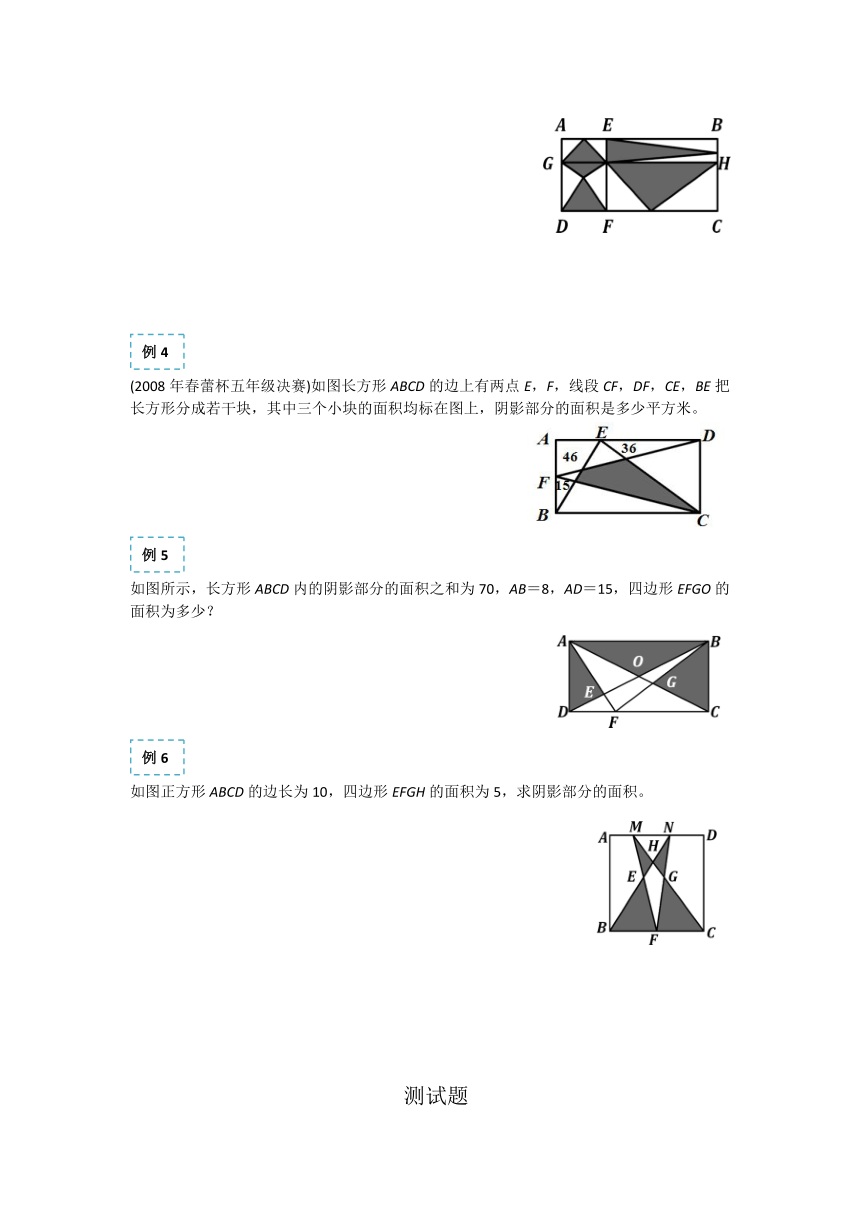
一、知识要点:
例1
下列是四个完全一样的长方形,其中阴影部分的面积( )
A.只有两个相等
B.只有三个相等
C.四个都相等
D.都不相等
例2
(第三届“华杯赛”初赛试题)一个长方形分成4个不同的三角形,绿色三角形的面积占长方形面积的0.15倍,黄色三角形的面积是21平方厘米,长方形的面积是多少平方厘米?
例3
如图四边形ABCD是长方形,EF与宽平行,GH与长平行,AB=8厘米,BC=6厘米,那么阴影部分的面积是多少平方厘米?
例4
(2008年春蕾杯五年级决赛)如图长方形ABCD的边上有两点E,F,线段CF,DF,CE,BE把长方形分成若干块,其中三个小块的面积均标在图上,阴影部分的面积是多少平方米。
例5
如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15,四边形EFGO的面积为多少?
例6
如图正方形ABCD的边长为10,四边形EFGH的面积为5,求阴影部分的面积。
测试题
1.如图所示正方形ABCD的边长为8,长方形EFGB的长BG=10,求长方形的宽。
2.如图O是长方形ABCD中的任意点,红色三角形的面积=5,绿色三角形的面积=13,求三角形BOD的面积。
3.如图所示,长方形ABCD的面积为24平方厘米,三角形ADM与三角形BCN的面积之和为7.8平方厘米,则四边形PMON的面积为多少平方厘米。
答案
1.答案:连接AG,三角形ABG的面积=正方形面积的一半=长方形面积的一半,所以正方形的面积=长方形的面积,长方形的宽=8×8÷10=6.4
2.答案:红色三角形+黄色三角形+三角形BOD的面积=黄色三角形+绿色三角形,所以红色三角形+三角形BOD=绿色三角形,三角形BOD的面积=13-5=8。
3.答案:三角形AOD的面积+三角形BOC的面积=三角形ABP的面积,所以三角形ADM与三角形BCN的面积之和=四边形PMON的面积+三角形AOB的面积,三角形AOB的面积=6平方厘米,所以四边形PMON的面积=7.8-6=1.8平方厘米。
一、知识要点:
例1
下列是四个完全一样的长方形,其中阴影部分的面积( )
A.只有两个相等
B.只有三个相等
C.四个都相等
D.都不相等
例2
(第三届“华杯赛”初赛试题)一个长方形分成4个不同的三角形,绿色三角形的面积占长方形面积的0.15倍,黄色三角形的面积是21平方厘米,长方形的面积是多少平方厘米?
例3
如图四边形ABCD是长方形,EF与宽平行,GH与长平行,AB=8厘米,BC=6厘米,那么阴影部分的面积是多少平方厘米?
例4
(2008年春蕾杯五年级决赛)如图长方形ABCD的边上有两点E,F,线段CF,DF,CE,BE把长方形分成若干块,其中三个小块的面积均标在图上,阴影部分的面积是多少平方米。
例5
如图所示,长方形ABCD内的阴影部分的面积之和为70,AB=8,AD=15,四边形EFGO的面积为多少?
例6
如图正方形ABCD的边长为10,四边形EFGH的面积为5,求阴影部分的面积。
测试题
1.如图所示正方形ABCD的边长为8,长方形EFGB的长BG=10,求长方形的宽。
2.如图O是长方形ABCD中的任意点,红色三角形的面积=5,绿色三角形的面积=13,求三角形BOD的面积。
3.如图所示,长方形ABCD的面积为24平方厘米,三角形ADM与三角形BCN的面积之和为7.8平方厘米,则四边形PMON的面积为多少平方厘米。
答案
1.答案:连接AG,三角形ABG的面积=正方形面积的一半=长方形面积的一半,所以正方形的面积=长方形的面积,长方形的宽=8×8÷10=6.4
2.答案:红色三角形+黄色三角形+三角形BOD的面积=黄色三角形+绿色三角形,所以红色三角形+三角形BOD=绿色三角形,三角形BOD的面积=13-5=8。
3.答案:三角形AOD的面积+三角形BOC的面积=三角形ABP的面积,所以三角形ADM与三角形BCN的面积之和=四边形PMON的面积+三角形AOB的面积,三角形AOB的面积=6平方厘米,所以四边形PMON的面积=7.8-6=1.8平方厘米。
同课章节目录
